MATLAB - Wielomiany

MATLAB reprezentuje wielomiany jako wektory wierszowe zawierające współczynniki uporządkowane według malejących potęg. Na przykład równanie P (x) = x ⁴ + 7x ³ - 5x + 9 można przedstawić jako -

p = [1 7 0–5 9];

Ocenianie wielomianów

Plik polyvalfunkcja służy do obliczania wielomianu o określonej wartości. Na przykład, aby ocenić nasz poprzedni wielomianp, przy x = 4, wpisz -

p = [1 7 0  -5 9];
polyval(p,4)

MATLAB wykonuje powyższe instrukcje i zwraca następujący wynik -

ans = 693

MATLAB zapewnia również polyvalmfunkcja do obliczania wielomianu macierzy. Wielomian macierzowy topolynomial z macierzami jako zmiennymi.

Na przykład, stwórzmy kwadratową macierz X i obliczmy wielomian p przy X -

p = [1 7 0  -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)

MATLAB wykonuje powyższe instrukcje i zwraca następujący wynik -

ans =
      2307       -1769        -939        4499
      2314       -2376        -249        4695
      2256       -1892        -549        4310
      4570       -4532       -1062        9269

Znajdowanie korzeni wielomianów

Plik rootsfunkcja oblicza pierwiastki wielomianu. Na przykład, aby obliczyć pierwiastki naszego wielomianu p, wpisz -

p = [1 7 0  -5 9];
r = roots(p)

MATLAB wykonuje powyższe instrukcje i zwraca następujący wynik -

r =
   -6.8661 + 0.0000i
   -1.4247 + 0.0000i
   0.6454 + 0.7095i
   0.6454 - 0.7095i

Funkcja polyjest odwrotnością funkcji pierwiastków i wraca do współczynników wielomianu. Na przykład -

p2 = poly(r)

MATLAB wykonuje powyższe instrukcje i zwraca następujący wynik -

p2 =

   Columns 1 through 3:

      1.00000 + 0.00000i   7.00000 + 0.00000i   0.00000 + 0.00000i

   Columns 4 and 5:

      -5.00000 - 0.00000i   9.00000 + 0.00000i

Dopasowanie krzywej wielomianowej

Plik polyfitfunkcja znajduje współczynniki wielomianu, który pasuje do zbioru danych w sensie najmniejszych kwadratów. Jeśli x i y są dwoma wektorami zawierającymi dane xiy, które mają zostać dopasowane do wielomianu n-stopniowego, to otrzymujemy wielomian pasujący do danych, pisząc -

p = polyfit(x,y,n)

Przykład

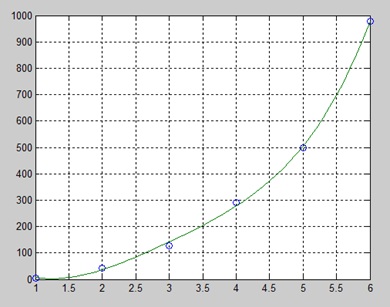
Utwórz plik skryptu i wpisz następujący kod -

x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67];   %data
p = polyfit(x,y,4)   %get the polynomial

% Compute the values of the polyfit estimate over a finer range, 
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;          
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on

Po uruchomieniu pliku MATLAB wyświetla następujący wynik -

p =
   4.1056  -47.9607  222.2598 -362.7453  191.1250

I wykreśla następujący wykres -