MATLAB - Szybki przewodnik
MATLAB (laboratorium macierzowe) to język programowania wysokiego poziomu czwartej generacji i interaktywne środowisko do obliczeń numerycznych, wizualizacji i programowania.
MATLAB jest rozwijany przez MathWorks.
Pozwala na manipulacje macierzą; wykreślanie funkcji i danych; implementacja algorytmów; tworzenie interfejsów użytkownika; współpraca z programami napisanymi w innych językach, w tym C, C ++, Java i FORTRAN; analizować dane; opracowywać algorytmy; i tworzyć modele i aplikacje.
Posiada wiele wbudowanych poleceń i funkcji matematycznych, które pomagają w obliczeniach matematycznych, generowaniu wykresów i wykonywaniu metod numerycznych.
MATLAB's Power of Computational Mathematics
MATLAB jest używany w każdym aspekcie matematyki obliczeniowej. Poniżej przedstawiono kilka powszechnie używanych obliczeń matematycznych, w których jest najczęściej używany -
- Radzenie sobie z macierzami i tablicami
- Drukowanie i grafika 2-W i 3-W
- Algebra liniowa
- Równania algebraiczne
- Funkcje nieliniowe
- Statistics
- Analiza danych
- Rachunek różniczkowy i równania różniczkowe
- Obliczenia numeryczne
- Integration
- Transforms
- Dopasowanie krzywej
- Różne inne funkcje specjalne
Cechy MATLAB
Oto podstawowe cechy MATLAB -
Jest to język wysokiego poziomu do obliczeń numerycznych, wizualizacji i tworzenia aplikacji.
Zapewnia również interaktywne środowisko do iteracyjnej eksploracji, projektowania i rozwiązywania problemów.
Zawiera obszerną bibliotekę funkcji matematycznych dla algebry liniowej, statystyki, analizy Fouriera, filtrowania, optymalizacji, całkowania numerycznego i rozwiązywania zwykłych równań różniczkowych.
Zawiera wbudowaną grafikę do wizualizacji danych oraz narzędzia do tworzenia niestandardowych wykresów.
Interfejs programistyczny MATLAB zapewnia narzędzia programistyczne do poprawy możliwości utrzymania jakości kodu i maksymalizacji wydajności.
Udostępnia narzędzia do tworzenia aplikacji z niestandardowymi interfejsami graficznymi.
Zapewnia funkcje do integracji algorytmów opartych na MATLAB z zewnętrznymi aplikacjami i językami, takimi jak C, Java, .NET i Microsoft Excel.
Zastosowania MATLAB
MATLAB jest szeroko stosowany jako narzędzie obliczeniowe w nauce i inżynierii, obejmujące dziedziny fizyki, chemii, matematyki i wszystkich dziedzin inżynierii. Jest używany w szeregu zastosowań, w tym:
- Przetwarzanie sygnału i komunikacja
- Przetwarzanie obrazu i wideo
- Systemy kontrolne
- Testowanie i pomiary
- Finanse obliczeniowe
- Biologia obliczeniowa
Konfiguracja środowiska lokalnego
Konfiguracja środowiska MATLAB to kwestia kilku kliknięć. Instalator można pobrać stąd .
MathWorks dostarcza licencjonowany produkt, wersję próbną oraz wersję studencką. Musisz zalogować się do serwisu i trochę poczekać na ich zatwierdzenie.
Po pobraniu instalatora oprogramowanie można zainstalować kilkoma kliknięciami.
Zrozumienie środowiska MATLAB
IDE programistyczne MATLAB można uruchomić za pomocą ikony utworzonej na pulpicie. Główne okno robocze MATLAB-a nosi nazwę pulpitu. Po uruchomieniu MATLAB pulpit pojawia się w domyślnym układzie -
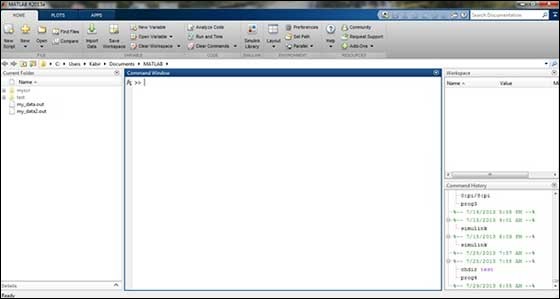
Pulpit ma następujące panele -
Current Folder - Ten panel umożliwia dostęp do folderów i plików projektu.
Command Window- Jest to główny obszar, w którym można wprowadzać polecenia w wierszu poleceń. Wskazuje na to wiersz polecenia (>>).
Workspace - Obszar roboczy pokazuje wszystkie utworzone i / lub importowane zmienne z plików.
Command History - Ten panel wyświetla lub zwraca polecenia wprowadzone w wierszu poleceń.


Skonfiguruj GNU Octave
Jeśli chcesz używać Octave na swoim komputerze (Linux, BSD, OS X lub Windows), pobierz najnowszą wersję z Download GNU Octave . Możesz sprawdzić podane instrukcje instalacji dla swojego komputera.
Środowisko MATLAB zachowuje się jak bardzo złożony kalkulator. Możesz wprowadzać polecenia w wierszu polecenia >>.
MATLAB to środowisko interpretowane. Innymi słowy, wydajesz polecenie, a MATLAB wykonuje je od razu.
Praktyka
Wpisz prawidłowe wyrażenie, na przykład
5 + 5I naciśnij ENTER
Kiedy klikniesz przycisk Wykonaj lub naciśniesz Ctrl + E, MATLAB wykona go natychmiast, a zwrócony wynik to -
ans = 10Weźmy jeszcze kilka przykładów -
3 ^ 2 % 3 raised to the power of 2Kiedy klikniesz przycisk Wykonaj lub naciśniesz Ctrl + E, MATLAB wykona go natychmiast, a zwrócony wynik to -
ans = 9Inny przykład,
sin(pi /2) % sine of angle 90oKiedy klikniesz przycisk Wykonaj lub naciśniesz Ctrl + E, MATLAB wykona go natychmiast, a zwrócony wynik to -
ans = 1Inny przykład,
7/0 % Divide by zeroKiedy klikniesz przycisk Wykonaj lub naciśniesz Ctrl + E, MATLAB wykona go natychmiast, a zwrócony wynik to -
ans = Inf
warning: division by zeroInny przykład,
732 * 20.3Kiedy klikniesz przycisk Wykonaj lub naciśniesz Ctrl + E, MATLAB wykona go natychmiast, a zwrócony wynik to -
ans = 1.4860e+04MATLAB zapewnia specjalne wyrażenia dla niektórych symboli matematycznych, takich jak pi dla π, Inf dla ∞, i (i j) dla √-1 itp. Nan oznacza „nie jest liczbą”.
Użycie średnika (;) w MATLAB
Średnik (;) oznacza koniec instrukcji. Jeśli jednak chcesz ukryć i ukryć dane wyjściowe MATLAB dla wyrażenia, dodaj średnik po wyrażeniu.
Na przykład,
x = 3;
y = x + 5Kiedy klikniesz przycisk Wykonaj lub naciśniesz Ctrl + E, MATLAB wykona go natychmiast, a zwrócony wynik to -
y = 8Dodawanie komentarzy
Symbol procentu (%) służy do wskazania wiersza komentarza. Na przykład,
x = 9 % assign the value 9 to xMożesz także napisać blok komentarzy, używając operatorów komentarzy blokowych% {i%}.
Edytor MATLAB zawiera narzędzia i elementy menu kontekstowego, które pomagają dodawać, usuwać lub zmieniać format komentarzy.
Powszechnie używane operatory i znaki specjalne
MATLAB obsługuje następujące powszechnie używane operatory i znaki specjalne -
| Operator | Cel, powód |
|---|---|
| + | Plus; operator dodawania. |
| - | Minus; operator odejmowania. |
| * | Operator mnożenia wartości skalarnej i macierzowej. |
| .* | Operator mnożenia tablicy. |
| ^ | Operator potęgowania skalarnego i macierzowego. |
| .^ | Operator potęgowania tablicy. |
| \ | Operator dzielenia lewostronnego. |
| / | Operator prawego podziału. |
| .\ | Operator dzielenia z lewej strony tablicy. |
| ./ | Operator prawego podziału tablicy. |
| : | Dwukropek; generuje regularnie rozmieszczone elementy i reprezentuje cały wiersz lub kolumnę. |
| ( ) | Zdanie wtrącone; obejmuje argumenty funkcji i indeksy tablic; zastępuje pierwszeństwo. |
| [ ] | Wsporniki; obudowy elementów tablicy. |
| . | Kropka dziesiętna. |
| … | Elipsa; operator kontynuacji linii |
| , | Przecinek; oddziela instrukcje i elementy w wierszu |
| ; | Średnik; oddziela kolumny i wyłącza wyświetlanie. |
| % | Znak procentu; oznacza komentarz i określa formatowanie. |
| _ | Cytuj znak i transponuj operator. |
| ._ | Nieskoniugowany operator transpozycji. |
| = | Operator przypisania. |
Specjalne zmienne i stałe
MATLAB obsługuje następujące specjalne zmienne i stałe -
| Nazwa | Znaczenie |
|---|---|
| ans | Najnowsza odpowiedź. |
| eps | Dokładność precyzji zmiennoprzecinkowej. |
| i,j | Jednostka urojona √-1. |
| Inf | Nieskończoność. |
| NaN | Niezdefiniowany wynik liczbowy (nie liczba). |
| pi | Liczba π |
Nazewnictwo zmiennych
Nazwy zmiennych składają się z litery, po której następuje dowolna liczba liter, cyfr lub podkreślenia.
MATLAB jest case-sensitive.
Nazwy zmiennych mogą mieć dowolną długość, jednak MATLAB używa tylko pierwszych N znaków, gdzie N podaje funkcja namelengthmax.
Zapisywanie Twojej pracy
Plik save Polecenie służy do zapisywania wszystkich zmiennych w obszarze roboczym, jako plik z rozszerzeniem .mat, w bieżącym katalogu.
Na przykład,
save myfileMożesz ponownie załadować plik w dowolnym momencie, używając rozszerzenia load Komenda.
load myfileW środowisku MATLAB każda zmienna jest tablicą lub macierzą.
Możesz przypisać zmienne w prosty sposób. Na przykład,
x = 3 % defining x and initializing it with a valueMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
x = 3Tworzy macierz 1 na 1 o nazwie x i przechowuje wartość 3 w swoim elemencie. Sprawdźmy inny przykład,
x = sqrt(16) % defining x and initializing it with an expressionMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
x = 4Należy pamiętać, że -
Po wprowadzeniu zmiennej do systemu możesz później odwołać się do niej.
Zmienne muszą mieć wartości, zanim zostaną użyte.
Gdy wyrażenie zwraca wynik, który nie jest przypisany do żadnej zmiennej, system przypisuje go do zmiennej o nazwie ans, której można użyć później.
Na przykład,
sqrt(78)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans = 8.8318Możesz użyć tej zmiennej ans -
sqrt(78);
9876/ansMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans = 1118.2Spójrzmy na inny przykład -
x = 7 * 8;
y = x * 7.89MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
y = 441.84Wiele przydziałów
Możesz mieć wiele przydziałów w tej samej linii. Na przykład,
a = 2; b = 7; c = a * bMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
c = 14Zapomniałem o zmiennych!
Plik who polecenie wyświetla wszystkie nazwy zmiennych, których użyłeś.
whoMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
Your variables are:
a ans b cPlik whos polecenie wyświetla niewiele więcej o zmiennych -
- Zmienne aktualnie w pamięci
- Typ każdej zmiennej
- Pamięć przydzielona do każdej zmiennej
- Czy są to zmienne złożone, czy nie
whosMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
Attr Name Size Bytes Class
==== ==== ==== ==== =====
a 1x1 8 double
ans 1x70 757 cell
b 1x1 8 double
c 1x1 8 double
Total is 73 elements using 781 bytesPlik clear polecenie usuwa wszystkie (lub określone) zmienne z pamięci.
clear x % it will delete x, won't display anything
clear % it will delete all variables in the workspace
% peacefully and unobtrusivelyDługie przydziały
Długie przypisania można rozszerzyć do innej linii za pomocą elips (...). Na przykład,
initial_velocity = 0;
acceleration = 9.8;
time = 20;
final_velocity = initial_velocity + acceleration * timeMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
final_velocity = 196Polecenie formatu
Domyślnie MATLAB wyświetla liczby z czterema wartościami miejsc dziesiętnych. Jest to znane jakoshort format.
Jeśli jednak chcesz uzyskać większą precyzję, musisz użyć format Komenda.
Plik format long polecenie wyświetla 16 cyfr po przecinku.
Na przykład -
format long
x = 7 + 10/3 + 5 ^ 1.2MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
x = 17.2319816406394Inny przykład,
format short
x = 7 + 10/3 + 5 ^ 1.2MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
x = 17.232Plik format bankpolecenie zaokrągla liczby do dwóch miejsc po przecinku. Na przykład,
format bank
daily_wage = 177.45;
weekly_wage = daily_wage * 6MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
weekly_wage = 1064.70MATLAB wyświetla duże liczby przy użyciu notacji wykładniczej.
Plik format short e Polecenie umożliwia wyświetlanie w formie wykładniczej z czterema miejscami po przecinku i wykładnikiem.
Na przykład,
format short e
4.678 * 4.9MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans = 2.2922e+01Plik format long ePolecenie umożliwia wyświetlanie w formie wykładniczej z czterema miejscami po przecinku i wykładnikiem. Na przykład,
format long e
x = piMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
x = 3.141592653589793e+00Plik format ratpolecenie daje najbliższe racjonalne wyrażenie wynikające z obliczeń. Na przykład,
format rat
4.678 * 4.9MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans = 34177/1491Tworzenie wektorów
Wektor to jednowymiarowa tablica liczb. MATLAB pozwala na tworzenie dwóch typów wektorów -
- Wektory wierszowe
- Wektory kolumnowe
Row vectors są tworzone przez umieszczenie zestawu elementów w nawiasach kwadratowych, przy użyciu spacji lub przecinka do oddzielenia elementów.
Na przykład,
r = [7 8 9 10 11]MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
r =
7 8 9 10 11Inny przykład,
r = [7 8 9 10 11];
t = [2, 3, 4, 5, 6];
res = r + tMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
res =
9 11 13 15 17Column vectors są tworzone przez umieszczenie zestawu elementów w nawiasach kwadratowych, przy użyciu średnika (;) do oddzielenia elementów.
c = [7; 8; 9; 10; 11]MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
c =
7
8
9
10
11Tworzenie macierzy
Macierz to dwuwymiarowa tablica liczb.
W MATLAB macierz jest tworzona przez wprowadzenie każdego wiersza jako sekwencji elementów oddzielonych spacjami lub przecinkami, a koniec wiersza jest oddzielany średnikiem. Na przykład stwórzmy macierz 3 na 3 jako -
m = [1 2 3; 4 5 6; 7 8 9]MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
m =
1 2 3
4 5 6
7 8 9MATLAB to interaktywny program do obliczeń numerycznych i wizualizacji danych. Możesz wprowadzić polecenie, wpisując je w wierszu polecenia MATLAB „>>” w plikuCommand Window.
W tej sekcji przedstawimy listę powszechnie używanych ogólnych poleceń MATLAB.
Polecenia dotyczące zarządzania sesją
MATLAB udostępnia różne polecenia do zarządzania sesją. Poniższa tabela zawiera wszystkie takie polecenia -
| Komenda | Cel, powód |
|---|---|
| clc | Czyści okno poleceń. |
| jasny | Usuwa zmienne z pamięci. |
| istnieć | Sprawdza istnienie pliku lub zmiennej. |
| światowy | Deklaruje zmienne jako globalne. |
| Wsparcie | Wyszukuje temat pomocy. |
| szukać | Przeszukuje wpisy pomocy dla słowa kluczowego. |
| porzucić | Zatrzymuje MATLAB. |
| WHO | Wyświetla aktualne zmienne. |
| kto | Wyświetla bieżące zmienne (długi wyświetlacz). |
Polecenia dotyczące pracy z systemem
MATLAB udostępnia różne przydatne polecenia do pracy z systemem, takie jak zapisywanie bieżącej pracy w obszarze roboczym jako plik i późniejsze ładowanie pliku.
Zapewnia również różne polecenia do innych czynności związanych z systemem, takich jak wyświetlanie daty, wyświetlanie plików w katalogu, wyświetlanie bieżącego katalogu itp.
W poniższej tabeli przedstawiono niektóre często używane polecenia związane z systemem -
| Komenda | Cel, powód |
|---|---|
| Płyta CD | Zmienia bieżący katalog. |
| data | Wyświetla aktualną datę. |
| usunąć | Usuwa plik. |
| Dziennik | Włącza / wyłącza nagrywanie pliku dziennika. |
| reż | Wyświetla wszystkie pliki w bieżącym katalogu. |
| Załaduj | Ładuje zmienne obszaru roboczego z pliku. |
| ścieżka | Wyświetla ścieżkę wyszukiwania. |
| pwd | Wyświetla bieżący katalog. |
| zapisać | Zapisuje zmienne obszaru roboczego w pliku. |
| rodzaj | Wyświetla zawartość pliku. |
| co | Wyświetla wszystkie pliki MATLAB w bieżącym katalogu. |
| wklread | Czyta plik arkusza kalkulacyjnego .wk1. |
Polecenia wejściowe i wyjściowe
MATLAB udostępnia następujące polecenia związane z wejściem i wyjściem -
| Komenda | Cel, powód |
|---|---|
| dysp | Wyświetla zawartość tablicy lub ciągu. |
| fscanf | Odczytaj sformatowane dane z pliku. |
| format | Kontroluje format wyświetlania ekranu. |
| fprintf | Wykonuje sformatowane zapisy na ekranie lub do pliku. |
| Wejście | Wyświetla monity i czeka na wprowadzenie danych. |
| ; | Eliminuje sitodruk. |
Plik fscanf i fprintfpolecenia zachowują się jak funkcje C scanf i printf. Obsługują następujące kody formatu -
| Kod formatu | Cel, powód |
|---|---|
| %s | Sformatuj jako ciąg. |
| %d | Sformatuj jako liczbę całkowitą. |
| %f | Sformatuj jako wartość zmiennoprzecinkową. |
| %e | Sformatuj jako wartość zmiennoprzecinkową w notacji naukowej. |
| %g | Sformatuj w najbardziej zwartej formie:% f lub% e. |
| \n | Wstaw nowy wiersz w ciągu wyjściowym. |
| \t | Wstaw tabulator do ciągu wyjściowego. |
Funkcja formatu ma następujące formularze używane do wyświetlania liczbowego -
| Funkcja formatu | Wyświetlaj do |
|---|---|
| format krótki | Cztery cyfry dziesiętne (domyślnie). |
| format długi | 16 cyfr dziesiętnych. |
| format krótki e | Pięć cyfr plus wykładnik. |
| format długi e | 16 cyfr plus wykładniki. |
| format banku | Dwie cyfry dziesiętne. |
| format + | Dodatnia, ujemna lub zero. |
| format szczur | Racjonalne przybliżenie. |
| format kompaktowy | Pomija niektóre wysuwy wiersza. |
| format luźny | Resetuje się do mniej kompaktowego trybu wyświetlania. |
Polecenia wektorowe, macierzowe i tablicowe
W poniższej tabeli przedstawiono różne polecenia używane do pracy z tablicami, macierzami i wektorami -
| Komenda | Cel, powód |
|---|---|
| kot | Łączy tablice. |
| odnaleźć | Znajduje indeksy niezerowych elementów. |
| długość | Oblicza liczbę elementów. |
| linspace | Tworzy wektor o regularnych odstępach. |
| logspace | Tworzy wektor z odstępami logarytmicznymi. |
| max | Zwraca największy element. |
| min | Zwraca najmniejszy element. |
| szturchać | Iloczyn każdej kolumny. |
| przefasonować | Zmienia rozmiar. |
| rozmiar | Oblicza rozmiar tablicy. |
| sortować | Sortuje każdą kolumnę. |
| suma | Sumuje każdą kolumnę. |
| oko | Tworzy macierz tożsamości. |
| jedynki | Tworzy tablicę jedynek. |
| zera | Tworzy tablicę zer. |
| krzyż | Oblicza iloczyn krzyżowy macierzy. |
| kropka | Oblicza iloczyn skalarny macierzy. |
| det | Oblicza wyznacznik tablicy. |
| inw | Oblicza odwrotność macierzy. |
| pinv | Oblicza pseudo odwrotność macierzy. |
| ranga | Oblicza rangę macierzy. |
| rref | Oblicza postać rzutu zredukowanego. |
| komórka | Tworzy tablicę komórek. |
| celldisp | Wyświetla tablicę komórek. |
| cellplot | Wyświetla graficzną reprezentację tablicy komórek. |
| num2cell | Konwertuje tablicę numeryczną na tablicę komórek. |
| rozdać | Dopasowuje listy wejściowe i wyjściowe. |
| iscell | Identyfikuje macierz komórek. |
Plotting Commands
MATLAB zapewnia liczne polecenia do rysowania wykresów. W poniższej tabeli przedstawiono niektóre z najczęściej używanych poleceń do drukowania -
| Komenda | Cel, powód |
|---|---|
| oś | Ustawia granice osi. |
| fplot | Inteligentne wykreślanie funkcji. |
| krata | Wyświetla linie siatki. |
| wątek | Generuje wykres XY. |
| wydrukować | Drukuje wydruk lub zapisuje wykres do pliku. |
| tytuł | Umieszcza tekst na górze działki. |
| xlabel | Dodaje etykietę tekstową do osi X. |
| ylabel | Dodaje etykietę tekstową do osi Y. |
| osie | Tworzy obiekty osi. |
| blisko | Zamyka bieżący wykres. |
| zamknij wszystko | Zamyka wszystkie działki. |
| postać | Otwiera nowe okno rysunku. |
| gtext | Umożliwia umieszczanie etykiet za pomocą myszy. |
| trzymać | Zawiesza bieżący wątek. |
| legenda | Umieszczanie legendy za pomocą myszy. |
| odświeżać | Przerysowuje okno aktualnej figury. |
| zestaw | Określa właściwości obiektów, takich jak osie. |
| wątek poboczny | Tworzy wykresy w podoknach. |
| tekst | Umieszcza ciąg na figurze. |
| bar | Tworzy wykres słupkowy. |
| loglog | Tworzy wykres dziennika. |
| polarny | Tworzy polarną fabułę. |
| semilogx | Tworzy działkę semilog. (logarytmiczna odcięta). |
| semilogia | Tworzy działkę semilog. (rzędna logarytmiczna). |
| schody | Tworzy działkę schodów. |
| trzon | Tworzy działkę macierzystą. |
Do tej pory używaliśmy środowiska MATLAB jako kalkulatora. Jednak MATLAB to także potężny język programowania, a także interaktywne środowisko obliczeniowe.
W poprzednich rozdziałach nauczyłeś się, jak wprowadzać polecenia z wiersza poleceń MATLAB. MATLAB pozwala również na zapisanie serii poleceń do pliku i wykonanie pliku jako kompletnej jednostki, na przykład pisanie funkcji i wywoływanie jej.
Pliki M.
MATLAB umożliwia zapisywanie dwóch rodzajów plików programowych -
Scripts - pliki skryptów to pliki programów z rozszerzeniem .m extension. W tych plikach piszesz serię poleceń, które chcesz wykonać razem. Skrypty nie akceptują danych wejściowych i nie zwracają żadnych danych wyjściowych. Działają na danych w obszarze roboczym.
Functions - pliki funkcji są również plikami programów z rozszerzeniem .m extension. Funkcje mogą przyjmować wejścia i wyjścia zwrotne. Zmienne wewnętrzne są lokalne dla funkcji.
Możesz użyć edytora MATLAB lub dowolnego innego edytora tekstu, aby utworzyć plik .makta. W tej sekcji omówimy pliki skryptów. Plik skryptu zawiera wiele kolejnych wierszy poleceń MATLAB i wywołań funkcji. Możesz uruchomić skrypt, wpisując jego nazwę w wierszu poleceń.
Tworzenie i uruchamianie pliku skryptu
Aby utworzyć pliki skryptów, musisz użyć edytora tekstu. Możesz otworzyć edytor MATLAB na dwa sposoby -
- Korzystanie z wiersza poleceń
- Korzystanie z IDE
Jeśli używasz wiersza polecenia, wpisz editw wierszu polecenia. Otworzy się edytor. Możesz bezpośrednio wpisaćedit a następnie nazwa pliku (z rozszerzeniem .m)
edit
Or
edit <filename>Powyższe polecenie utworzy plik w domyślnym katalogu MATLAB. Jeśli chcesz przechowywać wszystkie pliki programów w określonym folderze, musisz podać całą ścieżkę.
Utwórzmy folder o nazwie progs. Wpisz następujące polecenia w wierszu polecenia (>>) -
mkdir progs % create directory progs under default directory
chdir progs % changing the current directory to progs
edit prog1.m % creating an m file named prog1.mJeśli tworzysz plik po raz pierwszy, MATLAB poprosi o potwierdzenie. Kliknij Tak.
Alternatywnie, jeśli używasz IDE, wybierz NOWY -> Skrypt. Spowoduje to również otwarcie edytora i utworzenie pliku o nazwie Bez tytułu. Możesz nazwać i zapisać plik po wpisaniu kodu.
Wpisz następujący kod w edytorze -
NoOfStudents = 6000;
TeachingStaff = 150;
NonTeachingStaff = 20;
Total = NoOfStudents + TeachingStaff ...
+ NonTeachingStaff;
disp(Total);Po utworzeniu i zapisaniu pliku możesz go uruchomić na dwa sposoby -
Kliknięcie Run przycisk w oknie edytora lub
Wystarczy wpisać nazwę pliku (bez rozszerzenia) w wierszu poleceń: >> prog1
Wiersz okna poleceń wyświetla wynik -
6170Przykład
Utwórz plik skryptu i wpisz następujący kod -
a = 5; b = 7;
c = a + b
d = c + sin(b)
e = 5 * d
f = exp(-d)Kiedy powyższy kod jest kompilowany i wykonywany, daje następujący wynik -
c = 12
d = 12.657
e = 63.285
f = 3.1852e-06MATLAB nie wymaga żadnej deklaracji typu ani instrukcji wymiaru. Ilekroć MATLAB napotka nową nazwę zmiennej, tworzy zmienną i przydziela odpowiednią przestrzeń pamięci.
Jeśli zmienna już istnieje, MATLAB zastępuje oryginalną zawartość nową treścią i przydziela nową przestrzeń do przechowywania, jeśli to konieczne.
Na przykład,
Total = 42Powyższa instrukcja tworzy macierz 1 na 1 o nazwie „Suma” i przechowuje w niej wartość 42.
Typy danych dostępne w MATLAB
MATLAB zapewnia 15 podstawowych typów danych. Każdy typ danych przechowuje dane w postaci macierzy lub tablicy. Rozmiar tej macierzy lub tablicy to co najmniej 0 na 0 i może wzrosnąć do macierzy lub tablicy o dowolnym rozmiarze.
Poniższa tabela przedstawia najczęściej używane typy danych w MATLAB -
| Sr.No. | Typ i opis danych |
|---|---|
| 1 | int8 8-bitowa liczba całkowita ze znakiem |
| 2 | uint8 8-bitowa liczba całkowita bez znaku |
| 3 | int16 16-bitowa liczba całkowita ze znakiem |
| 4 | uint16 16-bitowa liczba całkowita bez znaku |
| 5 | int32 32-bitowa liczba całkowita ze znakiem |
| 6 | uint32 32-bitowa liczba całkowita bez znaku |
| 7 | int64 64-bitowa liczba całkowita ze znakiem |
| 8 | uint64 64-bitowa liczba całkowita bez znaku |
| 9 | single dane liczbowe o pojedynczej precyzji |
| 10 | double dane liczbowe podwójnej precyzji |
| 11 | logical wartości logiczne 1 lub 0 reprezentują odpowiednio prawdę i fałsz |
| 12 | char dane znakowe (łańcuchy są przechowywane jako wektor znaków) |
| 13 | cell array tablica indeksowanych komórek, z których każda może przechowywać tablicę o innym wymiarze i typie danych |
| 14 | structure Struktury podobne do C, każda struktura ma nazwane pola, które mogą przechowywać tablicę o innym wymiarze i typie danych |
| 15 | function handle wskaźnik do funkcji |
| 16 | user classes obiekty zbudowane z klasy zdefiniowanej przez użytkownika |
| 17 | java classes obiekty zbudowane z klasy Java |
Przykład
Utwórz plik skryptu z następującym kodem -
str = 'Hello World!'
n = 2345
d = double(n)
un = uint32(789.50)
rn = 5678.92347
c = int32(rn)Kiedy powyższy kod jest kompilowany i wykonywany, daje następujący wynik -
str = Hello World!
n = 2345
d = 2345
un = 790
rn = 5678.9
c = 5679Konwersja typu danych
MATLAB zapewnia różne funkcje do konwersji wartości z jednego typu danych na inny. W poniższej tabeli przedstawiono funkcje konwersji typu danych -
| Funkcjonować | Cel, powód |
|---|---|
| zwęglać | Konwertuj na tablicę znaków (ciąg) |
| int2str | Konwertuj dane całkowite na ciąg |
| mat2str | Konwertuj macierz na ciąg |
| num2str | Konwertuj liczbę na ciąg |
| str2double | Konwertuj ciąg na wartość o podwójnej precyzji |
| str2num | Konwertuj ciąg na liczbę |
| native2unicode | Konwertuj bajty numeryczne na znaki Unicode |
| unicode2native | Konwertuj znaki Unicode na bajty numeryczne |
| base2dec | Konwertuj podstawowy ciąg liczbowy N na liczbę dziesiętną |
| bin2dec | Konwertuj ciąg liczb binarnych na liczbę dziesiętną |
| dec2base | Konwertuj liczbę dziesiętną na podstawową liczbę N w ciągu |
| dec2bin | Zamień liczbę dziesiętną na dwójkową w ciągu |
| dec2hex | Konwertuj liczbę dziesiętną na szesnastkową w ciągu |
| hex2dec | Konwertuj szesnastkowy ciąg liczbowy na liczbę dziesiętną |
| hex2num | Konwertuj szesnastkowy ciąg liczbowy na liczbę podwójnej precyzji |
| num2hex | Konwertuj pojedyncze i podwójne na ciągi szesnastkowe IEEE |
| cell2mat | Konwertuj tablicę komórek na tablicę numeryczną |
| cell2struct | Konwertuj tablicę komórek na tablicę struktur |
| cellstr | Utwórz tablicę komórek zawierającą ciągi znaków z tablicy znaków |
| mat2cell | Konwertuj tablicę na tablicę komórek z potencjalnie różnymi rozmiarami komórek |
| num2cell | Konwertuj tablicę na tablicę komórek z komórkami o stałym rozmiarze |
| struct2cell | Konwertuj strukturę na tablicę komórek |
Określenie typów danych
MATLAB zapewnia różne funkcje do identyfikowania typu danych zmiennej.
Poniższa tabela zawiera funkcje służące do określania typu danych zmiennej -
| Funkcjonować | Cel, powód |
|---|---|
| jest | Wykryj stan |
| jest | Sprawdź, czy wejście jest obiektem określonej klasy |
| iscell | Określ, czy dane wejściowe to tablica komórek |
| iscellstr | Określ, czy dane wejściowe to tablica komórek zawierająca ciągi |
| ischar | Określ, czy element jest tablicą znaków |
| isfield | Określ, czy wejście jest polem tablicy strukturalnej |
| jest na powierzchni | Określ, czy dane wejściowe są tablicą zmiennoprzecinkową |
| ishghandle | Prawda dla uchwytów obiektów Handle Graphics |
| isinteger | Sprawdź, czy wejście jest tablicą liczb całkowitych |
| isjava | Sprawdź, czy dane wejściowe są obiektem Java |
| islogical | Sprawdź, czy wejście jest tablicą logiczną |
| isnumeric | Sprawdź, czy dane wejściowe to tablica numeryczna |
| isobject | Sprawdź, czy dane wejściowe to obiekt MATLAB |
| jest realne | Sprawdź, czy wejście jest prawdziwą tablicą |
| isscalar | Określ, czy dane wejściowe są skalarne |
| isstr | Określ, czy dane wejściowe to tablica znaków |
| isstruct | Określ, czy dane wejściowe to tablica strukturalna |
| isvector | Określ, czy wejście jest wektorem |
| klasa | Określ klasę obiektu |
| validateattributes | Sprawdź poprawność tablicy |
| kto | Lista zmiennych w obszarze roboczym, wraz z rozmiarami i typami |
Przykład
Utwórz plik skryptu z następującym kodem -
x = 3
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
x = 23.54
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
x = [1 2 3]
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
x = 'Hello'
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)Po uruchomieniu pliku daje on następujący wynik -
x = 3
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x = 23.540
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x =
1 2 3
ans = 0
ans = 1
ans = 1
ans = 0
x = Hello
ans = 0
ans = 0
ans = 1
ans = 0
ans = 0Operator to symbol, który mówi kompilatorowi, aby wykonał określone operacje matematyczne lub logiczne. MATLAB jest zaprojektowany do działania przede wszystkim na całych macierzach i tablicach. Dlatego operatory w MATLAB-ie działają zarówno na danych skalarnych, jak i nieskalarnych. MATLAB umożliwia następujące typy podstawowych operacji -
- Operatory arytmetyczne
- Operatorzy relacyjni
- Operatory logiczne
- Operacje bitowe
- Operacje na zbiorach
Operatory arytmetyczne
MATLAB pozwala na dwa różne rodzaje operacji arytmetycznych -
- Operacje arytmetyczne na macierzach
- Operacje arytmetyczne na tablicach
Operacje arytmetyczne na macierzach są takie same, jak w algebrze liniowej. Operacje na tablicach są wykonywane element po elemencie, zarówno na jednowymiarowej, jak i wielowymiarowej tablicy.
Operatory macierzowe i operatory tablicowe są rozróżniane za pomocą symbolu kropki (.). Jednak ponieważ operacje dodawania i odejmowania są takie same dla macierzy i tablic, operator jest taki sam w obu przypadkach. Poniższa tabela zawiera krótki opis operatorów -
Pokaż przykłady
| Sr.No. | Operator i opis |
|---|---|
| 1 | + Dodatek lub jednoargumentowy plus. A + B dodaje wartości przechowywane w zmiennych A i B. A i B muszą mieć ten sam rozmiar, chyba że jeden jest skalarem. Do macierzy o dowolnej wielkości można dodać skalar. |
| 2 | - Odejmowanie lub jednoargumentowy minus. AB odejmuje wartość B od A. A i B muszą mieć ten sam rozmiar, chyba że jeden jest skalarem. Z macierzy o dowolnej wielkości można odjąć skalar. |
| 3 | * Mnożenie macierzy. C = A * B jest liniowym iloczynem algebraicznym macierzy A i B. Dokładniej,
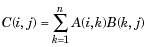
Dla nieskalarnych A i B liczba kolumn A musi być równa liczbie wierszy B. Skalar może pomnożyć macierz dowolnej wielkości. |
| 4 | .* Mnożenie tablicy. A. * B jest iloczynem element po elemencie tablic A i B. A i B muszą mieć ten sam rozmiar, chyba że jeden z nich jest skalarem. |
| 5 | / Ukośnik lub prawy podział macierzy. B / A jest mniej więcej tym samym, co B * inv (A). Dokładniej, B / A = (A '\ B') '. |
| 6 | ./ Prawidłowy podział tablicy. A./B to macierz z elementami A (i, j) / B (i, j). A i B muszą mieć ten sam rozmiar, chyba że jeden z nich jest skalarem. |
| 7 | \ Lewy ukośnik lub podział macierzy z lewej strony. Jeśli A jest macierzą kwadratową, A \ B jest mniej więcej tym samym, co inv (A) * B, z wyjątkiem tego, że jest obliczane w inny sposób. Jeżeli A oznacza grupę n-o-N matrycy i B jest wektorem kolumny z elementami N lub matryca z kilku takich kolumn, a X = A \ B jest rozwiązaniem równania AX = B . Komunikat ostrzegawczy jest wyświetlany, jeśli A jest źle wyskalowane lub prawie pojedyncze. |
| 8 | .\ Lewy podział tablicy. A. \ B to macierz z elementami B (i, j) / A (i, j). A i B muszą mieć ten sam rozmiar, chyba że jeden z nich jest skalarem. |
| 9 | ^ Moc matrycy. X ^ p jest X do potęgi p, jeśli p jest skalarem. Jeśli p jest liczbą całkowitą, moc obliczana jest przez powtórne podniesienie do kwadratu. Jeśli liczba całkowita jest ujemna, X jest odwracany jako pierwszy. W przypadku innych wartości p obliczenia obejmują wartości własne i wektory własne, tak że jeśli [V, D] = eig (X), to X ^ p = V * D. ^ p / V. |
| 10 | .^ Array power. A.^B is the matrix with elements A(i,j) to the B(i,j) power. A and B must have the same size, unless one of them is a scalar. |
| 11 | ' Matrix transpose. A' is the linear algebraic transpose of A. For complex matrices, this is the complex conjugate transpose. |
| 12 | .' Array transpose. A.' is the array transpose of A. For complex matrices, this does not involve conjugation. |
Relational Operators
Relational operators can also work on both scalar and non-scalar data. Relational operators for arrays perform element-by-element comparisons between two arrays and return a logical array of the same size, with elements set to logical 1 (true) where the relation is true and elements set to logical 0 (false) where it is not.
The following table shows the relational operators available in MATLAB −
Show Examples
| Sr.No. | Operator & Description |
|---|---|
| 1 | < Less than |
| 2 | <= Less than or equal to |
| 3 | > Greater than |
| 4 | >= Greater than or equal to |
| 5 | == Equal to |
| 6 | ~= Not equal to |
Logical Operators
MATLAB offers two types of logical operators and functions −
Element-wise − These operators operate on corresponding elements of logical arrays.
Short-circuit − These operators operate on scalar and, logical expressions.
Element-wise logical operators operate element-by-element on logical arrays. The symbols &, |, and ~ are the logical array operators AND, OR, and NOT.
Short-circuit logical operators allow short-circuiting on logical operations. The symbols && and || are the logical short-circuit operators AND and OR.
Show Examples
Bitwise Operations
Bitwise operators work on bits and perform bit-by-bit operation. The truth tables for &, |, and ^ are as follows −
| p | q | p & q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Assume if A = 60; and B = 13; Now in binary format they will be as follows −
A = 0011 1100
B = 0000 1101
-----------------
A&B = 0000 1100
A|B = 0011 1101
A^B = 0011 0001
~A = 1100 0011
MATLAB provides various functions for bit-wise operations like 'bitwise and', 'bitwise or' and 'bitwise not' operations, shift operation, etc.
The following table shows the commonly used bitwise operations −
Show Examples
| Function | Purpose |
|---|---|
| bitand(a, b) | Bit-wise AND of integers a and b |
| bitcmp(a) | Bit-wise complement of a |
| bitget(a,pos) | Get bit at specified position pos, in the integer array a |
| bitor(a, b) | Bit-wise OR of integers a and b |
| bitset(a, pos) | Set bit at specific location pos of a |
| bitshift(a, k) | Returns a shifted to the left by k bits, equivalent to multiplying by 2k. Negative values of k correspond to shifting bits right or dividing by 2|k| and rounding to the nearest integer towards negative infinite. Any overflow bits are truncated. |
| bitxor(a, b) | Bit-wise XOR of integers a and b |
| swapbytes | Swap byte ordering |
Set Operations
MATLAB provides various functions for set operations, like union, intersection and testing for set membership, etc.
The following table shows some commonly used set operations −
Show Examples
| Sr.No. | Function & Description |
|---|---|
| 1 | intersect(A,B) Set intersection of two arrays; returns the values common to both A and B. The values returned are in sorted order. |
| 2 | intersect(A,B,'rows') Treats each row of A and each row of B as single entities and returns the rows common to both A and B. The rows of the returned matrix are in sorted order. |
| 3 | ismember(A,B) Returns an array the same size as A, containing 1 (true) where the elements of A are found in B. Elsewhere, it returns 0 (false). |
| 4 | ismember(A,B,'rows') Treats each row of A and each row of B as single entities and returns a vector containing 1 (true) where the rows of matrix A are also rows of B. Elsewhere, it returns 0 (false). |
| 5 | issorted(A) Returns logical 1 (true) if the elements of A are in sorted order and logical 0 (false) otherwise. Input A can be a vector or an N-by-1 or 1-by-N cell array of strings. A is considered to be sorted if A and the output of sort(A) are equal. |
| 6 | issorted(A, 'rows') Returns logical 1 (true) if the rows of two-dimensional matrix A is in sorted order, and logical 0 (false) otherwise. Matrix A is considered to be sorted if A and the output of sortrows(A) are equal. |
| 7 | setdiff(A,B) Sets difference of two arrays; returns the values in A that are not in B. The values in the returned array are in sorted order. |
| 8 | setdiff(A,B,'rows') Treats each row of A and each row of B as single entities and returns the rows from A that are not in B. The rows of the returned matrix are in sorted order. The 'rows' option does not support cell arrays. |
| 9 | setxor Sets exclusive OR of two arrays |
| 10 | union Sets union of two arrays |
| 11 | unique Unique values in array |
Decision making structures require that the programmer should specify one or more conditions to be evaluated or tested by the program, along with a statement or statements to be executed if the condition is determined to be true, and optionally, other statements to be executed if the condition is determined to be false.
Following is the general form of a typical decision making structure found in most of the programming languages −
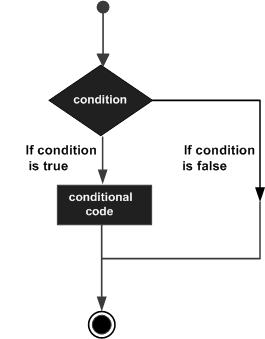
MATLAB provides following types of decision making statements. Click the following links to check their detail −
| Sr.No. | Statement & Description |
|---|---|
| 1 | if ... end statement An if ... end statement consists of a boolean expression followed by one or more statements. |
| 2 | if...else...end statement An if statement can be followed by an optional else statement, which executes when the boolean expression is false. |
| 3 | If... elseif...elseif...else...end statements An if statement can be followed by one (or more) optional elseif... and an else statement, which is very useful to test various conditions. |
| 4 | nested if statements You can use one if or elseif statement inside another if or elseif statement(s). |
| 5 | switch statement A switch statement allows a variable to be tested for equality against a list of values. |
| 6 | nested switch statements You can use one switch statement inside another switch statement(s). |
There may be a situation when you need to execute a block of code several number of times. In general, statements are executed sequentially. The first statement in a function is executed first, followed by the second, and so on.
Programming languages provide various control structures that allow for more complicated execution paths.
A loop statement allows us to execute a statement or group of statements multiple times and following is the general form of a loop statement in most of the programming languages −
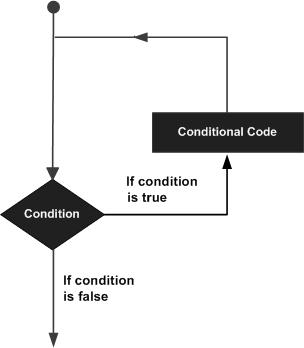
MATLAB provides following types of loops to handle looping requirements. Click the following links to check their detail −
| Sr.No. | Loop Type & Description |
|---|---|
| 1 | while loop Repeats a statement or group of statements while a given condition is true. It tests the condition before executing the loop body. |
| 2 | for loop Executes a sequence of statements multiple times and abbreviates the code that manages the loop variable. |
| 3 | nested loops You can use one or more loops inside any another loop. |
Loop Control Statements
Loop control statements change execution from its normal sequence. When execution leaves a scope, all automatic objects that were created in that scope are destroyed.
MATLAB supports the following control statements. Click the following links to check their detail.
| Sr.No. | Control Statement & Description |
|---|---|
| 1 | break statement Terminates the loop statement and transfers execution to the statement immediately following the loop. |
| 2 | continue statement Causes the loop to skip the remainder of its body and immediately retest its condition prior to reiterating. |
A vector is a one-dimensional array of numbers. MATLAB allows creating two types of vectors −
- Row vectors
- Column vectors
Row Vectors
Row vectors are created by enclosing the set of elements in square brackets, using space or comma to delimit the elements.
r = [7 8 9 10 11]MATLAB will execute the above statement and return the following result −
r =
7 8 9 10 11Column Vectors
Column vectors are created by enclosing the set of elements in square brackets, using semicolon to delimit the elements.
c = [7; 8; 9; 10; 11]MATLAB will execute the above statement and return the following result −
c =
7
8
9
10
11Referencing the Elements of a Vector
You can reference one or more of the elements of a vector in several ways. The ith component of a vector v is referred as v(i). For example −
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(3)MATLAB will execute the above statement and return the following result −
ans = 3When you reference a vector with a colon, such as v(:), all the components of the vector are listed.
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(:)MATLAB will execute the above statement and return the following result −
ans =
1
2
3
4
5
6MATLAB allows you to select a range of elements from a vector.
For example, let us create a row vector rv of 9 elements, then we will reference the elements 3 to 7 by writing rv(3:7) and create a new vector named sub_rv.
rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)MATLAB will execute the above statement and return the following result −
sub_rv =
3 4 5 6 7Vector Operations
In this section, let us discuss the following vector operations −
Addition and Subtraction of Vectors
Scalar Multiplication of Vectors
Transpose of a Vector
Appending Vectors
Magnitude of a Vector
Vector Dot Product
Vectors with Uniformly Spaced Elements
A matrix is a two-dimensional array of numbers.
In MATLAB, you create a matrix by entering elements in each row as comma or space delimited numbers and using semicolons to mark the end of each row.
For example, let us create a 4-by-5 matrix a −
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]MATLAB will execute the above statement and return the following result −
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8Referencing the Elements of a Matrix
To reference an element in the mth row and nth column, of a matrix mx, we write −
mx(m, n);Na przykład, w odniesieniu do elementu w 2 -go rzędu a 5 th kolumny macierzy A , a utworzony w poprzednim rozdziale typem -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(2,5)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans = 6Aby odwołać się do wszystkich elementów w m- tej kolumnie, wpisujemy A (:, m).
Utwórzmy wektor kolumnowy v z elementów czwartego rzędu macierzy a -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
v = a(:,4)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
v =
4
5
6
7Można również wybrać elementy w m TH do n th kolumn, w tym piszemy -
a(:,m:n)Stwórzmy mniejszą macierz, biorąc elementy z drugiej i trzeciej kolumny -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
2 3
3 4
4 5
5 6W ten sam sposób możesz utworzyć podmacierz, biorąc podrzędną część macierzy.
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
2 3
3 4
4 5
5 6W ten sam sposób możesz utworzyć podmacierz, biorąc podrzędną część macierzy.
Na przykład, stwórzmy podmacierz sa przyjmującą wewnętrzną część -
3 4 5
4 5 6Aby to zrobić, napisz -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
sa = a(2:3,2:4)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
sa =
3 4 5
4 5 6Usuwanie wiersza lub kolumny w macierzy
Możesz usunąć cały wiersz lub kolumnę macierzy, przypisując pusty zestaw nawiasów kwadratowych [] do tego wiersza lub kolumny. Zasadniczo [] oznacza pustą tablicę.
Na przykład usuńmy czwarty wiersz -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a( 4 , : ) = []MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7Następnie usuńmy piątą kolumnę -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(: , 5)=[]MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
a =
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7Przykład
W tym przykładzie stwórzmy macierz 3 na 3 m, a następnie dwukrotnie skopiujemy drugi i trzeci wiersz tej macierzy, aby utworzyć macierz 4 na 3.
Utwórz plik skryptu z następującym kodem -
a = [ 1 2 3 ; 4 5 6; 7 8 9];
new_mat = a([2,3,2,3],:)Po uruchomieniu pliku wyświetla następujący wynik -
new_mat =
4 5 6
7 8 9
4 5 6
7 8 9Operacje na macierzach
W tej sekcji omówimy następujące podstawowe i powszechnie używane operacje macierzowe -
Dodawanie i odejmowanie macierzy
Podział macierzy
Operacje skalarne na macierzach
Transpozycja macierzy
Macierze konkatenacji
Mnożenie macierzy
Wyznacznik macierzy
Odwrotność macierzy
Wszystkie zmienne wszystkich typów danych w programie MATLAB są tablicami wielowymiarowymi. Wektor to jednowymiarowa tablica, a macierz to dwuwymiarowa tablica.
Omówiliśmy już wektory i macierze. W tym rozdziale omówimy tablice wielowymiarowe. Jednak wcześniej omówimy kilka specjalnych typów tablic.
Specjalne tablice w MATLAB
W tej sekcji omówimy niektóre funkcje, które tworzą specjalne tablice. Dla wszystkich tych funkcji pojedynczy argument tworzy tablicę kwadratową, podwójne argumenty tworzą tablicę prostokątną.
Plik zeros() funkcja tworzy tablicę wszystkich zer -
Na przykład -
zeros(5)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0Plik ones() funkcja tworzy tablicę wszystkich jedynek -
Na przykład -
ones(4,3)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
1 1 1
1 1 1
1 1 1
1 1 1Plik eye() funkcja tworzy macierz tożsamości.
Na przykład -
eye(4)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1Plik rand() funkcja tworzy tablicę równomiernie rozłożonych liczb losowych na (0,1) -
Na przykład -
rand(3, 5)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
0.8147 0.9134 0.2785 0.9649 0.9572
0.9058 0.6324 0.5469 0.1576 0.4854
0.1270 0.0975 0.9575 0.9706 0.8003Magiczny kwadrat
ZA magic square jest kwadratem, który daje tę samą sumę, gdy jego elementy są dodawane wierszami, kolumnami lub ukośnie.
Plik magic()funkcja tworzy magiczną tablicę kwadratową. Potrzeba pojedynczego argumentu, który podaje rozmiar kwadratu. Argument musi być wartością skalarną większą lub równą 3.
magic(4)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1Tablice wielowymiarowe
Tablica mająca więcej niż dwa wymiary nazywana jest tablicą wielowymiarową w MATLAB. Tablice wielowymiarowe w MATLAB są rozszerzeniem normalnej macierzy dwuwymiarowej.
Generalnie, aby wygenerować tablicę wielowymiarową, najpierw tworzymy tablicę dwuwymiarową i rozszerzamy ją.
Na przykład utwórzmy dwuwymiarową tablicę a.
a = [7 9 5; 6 1 9; 4 3 2]MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
a =
7 9 5
6 1 9
4 3 2Tablica a jest tablicą 3 na 3; możemy dodać trzeci wymiar do a , podając wartości takie jak -
a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
a =
ans(:,:,1) =
0 0 0
0 0 0
0 0 0
ans(:,:,2) =
1 2 3
4 5 6
7 8 9Możemy również tworzyć tablice wielowymiarowe za pomocą funkcji jedynek (), zer () lub rand ().
Na przykład,
b = rand(4,3,2)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
b(:,:,1) =
0.0344 0.7952 0.6463
0.4387 0.1869 0.7094
0.3816 0.4898 0.7547
0.7655 0.4456 0.2760
b(:,:,2) =
0.6797 0.4984 0.2238
0.6551 0.9597 0.7513
0.1626 0.3404 0.2551
0.1190 0.5853 0.5060Możemy również użyć cat()funkcję budowania wielowymiarowych tablic. Łączy listę tablic wzdłuż określonego wymiaru -
Składnia funkcji cat () to -
B = cat(dim, A1, A2...)Gdzie,
B to nowa utworzona tablica
A1 , A2 , ... to tablice do konkatenacji
dim jest wymiarem, wzdłuż którego mają być łączone tablice
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
a = [9 8 7; 6 5 4; 3 2 1];
b = [1 2 3; 4 5 6; 7 8 9];
c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])Po uruchomieniu pliku wyświetla się -
c(:,:,1) =
9 8 7
6 5 4
3 2 1
c(:,:,2) =
1 2 3
4 5 6
7 8 9
c(:,:,3) =
2 3 1
4 7 8
3 9 0Funkcje tablicowe
MATLAB zapewnia następujące funkcje do sortowania, obracania, permutacji, zmiany kształtu lub przesuwania zawartości tablicy.
| Funkcjonować | Cel, powód |
|---|---|
| długość | Długość wektora lub największego wymiaru tablicy |
| ndims | Liczba wymiarów tablicy |
| numel | Liczba elementów tablicy |
| rozmiar | Wymiary tablicy |
| iscolumn | Określa, czy dane wejściowe są wektorem kolumnowym |
| jest pusty | Określa, czy tablica jest pusta |
| ismatrix | Określa, czy dane wejściowe to macierz |
| isrow | Określa, czy dane wejściowe są wektorem wiersza |
| isscalar | Określa, czy dane wejściowe są skalarne |
| isvector | Określa, czy dane wejściowe są wektorowe |
| blkdiag | Konstruuje blokową macierz przekątną z argumentów wejściowych |
| Circshift | Przesuwa tablicę cyklicznie |
| ctranspoza | Złożona transpozycja koniugatu |
| diag | Macierze diagonalne i przekątne macierzy |
| flipdim | Odwraca tablicę wzdłuż określonego wymiaru |
| fliplr | Odwraca macierz od lewej do prawej |
| flipud | Odwraca macierz z góry na dół |
| ipermute | Odwraca permute wymiary tablicy ND |
| przestawiać | Przestawia wymiary tablicy ND |
| repmat | Replikuje i szyk kafelków |
| przefasonować | Zmienia kształt tablicy |
| rot90 | Obraca matrycę o 90 stopni |
| shiftdim | Przesuwa wymiary |
| jest posortowany | Określa, czy elementy zestawu są posortowane |
| sortować | Sortuje elementy tablicy w kolejności rosnącej lub malejącej |
| sortrows | Sortuje wiersze w kolejności rosnącej |
| ściskać | Usuwa pojedyncze wymiary |
| transponować | Transponować |
| wektoryzować | Wektoryzuje wyrażenie |
Przykłady
Poniższe przykłady ilustrują niektóre z wyżej wymienionych funkcji.
Length, Dimension and Number of elements −
Utwórz plik skryptu i wpisz w nim następujący kod -
x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9];
length(x) % length of x vector
y = rand(3, 4, 5, 2);
ndims(y) % no of dimensions in array y
s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab'];
numel(s) % no of elements in sPo uruchomieniu pliku wyświetla następujący wynik -
ans = 8
ans = 4
ans = 23Circular Shifting of the Array Elements −
Utwórz plik skryptu i wpisz w nim następujący kod -
a = [1 2 3; 4 5 6; 7 8 9] % the original array a
b = circshift(a,1) % circular shift first dimension values down by 1.
c = circshift(a,[1 -1]) % circular shift first dimension values % down by 1
% and second dimension values to the left % by 1.Po uruchomieniu pliku wyświetla następujący wynik -
a =
1 2 3
4 5 6
7 8 9
b =
7 8 9
1 2 3
4 5 6
c =
8 9 7
2 3 1
5 6 4Sortowanie tablic
Utwórz plik skryptu i wpisz w nim następujący kod -
v = [ 23 45 12 9 5 0 19 17] % horizontal vector
sort(v) % sorting v
m = [2 6 4; 5 3 9; 2 0 1] % two dimensional array
sort(m, 1) % sorting m along the row
sort(m, 2) % sorting m along the columnPo uruchomieniu pliku wyświetla następujący wynik -
v =
23 45 12 9 5 0 19 17
ans =
0 5 9 12 17 19 23 45
m =
2 6 4
5 3 9
2 0 1
ans =
2 0 1
2 3 4
5 6 9
ans =
2 4 6
3 5 9
0 1 2Tablica komórek
Macierze komórek to tablice indeksowanych komórek, w których każda komórka może przechowywać tablicę o różnych wymiarach i typach danych.
Plik cellfunkcja służy do tworzenia tablicy komórek. Składnia funkcji komórki to -
C = cell(dim)
C = cell(dim1,...,dimN)
D = cell(obj)Gdzie,
C to tablica komórek;
dim to skalarna liczba całkowita lub wektor liczb całkowitych, który określa wymiary tablicy komórek C;
dim1, ..., dimN to skalarne liczby całkowite, które określają wymiary C;
obj jest jednym z następujących -
- Tablica lub obiekt Java
- Tablica .NET typu System.String lub System.Object
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
c = cell(2, 5);
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}Po uruchomieniu pliku wyświetla następujący wynik -
c =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
[1,3] = Green
[2,3] = 3
[1,4] = Yellow
[2,4] = 4
[1,5] = White
[2,5] = 5
}Dostęp do danych w tablicach komórek
Istnieją dwa sposoby odwoływania się do elementów tablicy komórek -
- Zamknięcie indeksów w pierwszym nawiasie (), aby odwołać się do zestawów komórek
- Ujęcie indeksów w nawiasy klamrowe {}, aby odwołać się do danych w poszczególnych komórkach
Gdy umieścisz indeksy w pierwszym nawiasie, oznacza to zbiór komórek.
Indeksy tablic komórek w gładkich nawiasach odnoszą się do zestawów komórek.
Na przykład -
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c(1:2,1:2)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
}Możesz również uzyskać dostęp do zawartości komórek, indeksując je za pomocą nawiasów klamrowych.
Na przykład -
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c{1, 2:4}MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans = Blue
ans = Green
ans = YellowPlik colon(:)jest jednym z najbardziej użytecznych operatorów w MATLAB-ie. Służy do tworzenia wektorów, tablic z indeksami dolnymi ispecify for iterations.
Jeśli chcesz utworzyć wektor wierszowy zawierający liczby całkowite od 1 do 10, piszesz -
1:10MATLAB wykonuje instrukcję i zwraca wektor wierszowy zawierający liczby całkowite od 1 do 10 -
ans =
1 2 3 4 5 6 7 8 9 10Jeśli chcesz określić wartość przyrostu inną niż jeden, na przykład -
100: -5: 50MATLAB wykonuje instrukcję i zwraca następujący wynik -
ans =
100 95 90 85 80 75 70 65 60 55 50Weźmy inny przykład -
0:pi/8:piMATLAB wykonuje instrukcję i zwraca następujący wynik -
ans =
Columns 1 through 7
0 0.3927 0.7854 1.1781 1.5708 1.9635 2.3562
Columns 8 through 9
2.7489 3.1416Możesz użyć operatora dwukropka, aby utworzyć wektor indeksów do wybierania wierszy, kolumn lub elementów tablic.
Poniższa tabela opisuje jego użycie w tym celu (miejmy macierz A) -
| Format | Cel, powód |
|---|---|
| A(:,j) | jest j-tą kolumną A. |
| A(i,:) | to i-ty rząd A. |
| A(:,:) | jest równoważną dwuwymiarową tablicą. W przypadku matryc jest to to samo, co w przypadku A. |
| A(j:k) | to A (j), A (j + 1), ..., A (k). |
| A(:,j:k) | to A (:, j), A (:, j + 1), ..., A (:, k). |
| A(:,:,k) | jest k- tą stroną trójwymiarowej tablicy A. |
| A(i,j,k,:) | jest wektorem w czterowymiarowej tablicy A. Wektor zawiera A (i, j, k, 1), A (i, j, k, 2), A (i, j, k, 3) i tak dalej. |
| A(:) | to wszystkie elementy A, traktowane jako jedna kolumna. Po lewej stronie instrukcji przypisania A (:) wypełnia A, zachowując jego kształt z poprzedniego. W tym przypadku prawa strona musi zawierać taką samą liczbę elementów jak A. |
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
A = [1 2 3 4; 4 5 6 7; 7 8 9 10]
A(:,2) % second column of A
A(:,2:3) % second and third column of A
A(2:3,2:3) % second and third rows and second and third columnsPo uruchomieniu pliku wyświetla następujący wynik -
A =
1 2 3 4
4 5 6 7
7 8 9 10
ans =
2
5
8
ans =
2 3
5 6
8 9
ans =
5 6
8 9MATLAB obsługuje różne klasy numeryczne, które obejmują liczby całkowite ze znakiem i bez znaku oraz liczby zmiennoprzecinkowe o pojedynczej i podwójnej precyzji. Domyślnie MATLAB przechowuje wszystkie wartości liczbowe jako liczby zmiennoprzecinkowe o podwójnej precyzji.
Możesz wybrać zapisywanie dowolnej liczby lub tablicy liczb jako liczb całkowitych lub jako liczb o pojedynczej precyzji.
Wszystkie typy liczbowe obsługują podstawowe operacje tablicowe i operacje matematyczne.
Konwersja na różne numeryczne typy danych
MATLAB zapewnia następujące funkcje do konwersji na różne numeryczne typy danych -
| Funkcjonować | Cel, powód |
|---|---|
| podwójnie | Konwertuje na liczbę o podwójnej precyzji |
| pojedynczy | Konwertuje na liczbę o pojedynczej precyzji |
| int8 | Konwertuje na 8-bitową liczbę całkowitą ze znakiem |
| int16 | Konwertuje na 16-bitową liczbę całkowitą ze znakiem |
| int32 | Konwertuje na 32-bitową liczbę całkowitą ze znakiem |
| int64 | Konwertuje na 64-bitową liczbę całkowitą ze znakiem |
| uint8 | Konwertuje na 8-bitową liczbę całkowitą bez znaku |
| uint16 | Konwertuje na 16-bitową liczbę całkowitą bez znaku |
| uint32 | Konwertuje na 32-bitową liczbę całkowitą bez znaku |
| uint64 | Konwertuje na 64-bitową liczbę całkowitą bez znaku |
Przykład
Utwórz plik skryptu i wpisz następujący kod -
x = single([5.32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5Po uruchomieniu pliku pokazuje następujący wynik -
x =
39.900 26.025 47.100
x =
39.900 26.025 47.100
x =
38 23 45
x =
38 23 45
x =
38 23 45
x =
38 23 45Przykład
Rozszerzmy nieco poprzedni przykład. Utwórz plik skryptu i wpisz następujący kod -
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
x = num2cell(x)Po uruchomieniu pliku pokazuje następujący wynik -
x =
38 23 45
x =
38 23 45
x =
{
[1,1] = 38
[1,2] = 23
[1,3] = 45
}Najmniejsze i największe liczby całkowite
Funkcje intmax() i intmin() zwracają maksymalne i minimalne wartości, które mogą być reprezentowane przez wszystkie typy liczb całkowitych.
Obie funkcje przyjmują jako argument typ danych integer, na przykład intmax (int8) lub intmin (int64) i zwracają maksymalne i minimalne wartości, które można reprezentować za pomocą typu danych integer.
Przykład
Poniższy przykład ilustruje, jak uzyskać najmniejsze i największe wartości liczb całkowitych. Utwórz plik skryptu i napisz w nim następujący kod -
% displaying the smallest and largest signed integer data
str = 'The range for int8 is:\n\t%d to %d ';
sprintf(str, intmin('int8'), intmax('int8'))
str = 'The range for int16 is:\n\t%d to %d ';
sprintf(str, intmin('int16'), intmax('int16'))
str = 'The range for int32 is:\n\t%d to %d ';
sprintf(str, intmin('int32'), intmax('int32'))
str = 'The range for int64 is:\n\t%d to %d ';
sprintf(str, intmin('int64'), intmax('int64'))
% displaying the smallest and largest unsigned integer data
str = 'The range for uint8 is:\n\t%d to %d ';
sprintf(str, intmin('uint8'), intmax('uint8'))
str = 'The range for uint16 is:\n\t%d to %d ';
sprintf(str, intmin('uint16'), intmax('uint16'))
str = 'The range for uint32 is:\n\t%d to %d ';
sprintf(str, intmin('uint32'), intmax('uint32'))
str = 'The range for uint64 is:\n\t%d to %d ';
sprintf(str, intmin('uint64'), intmax('uint64'))Po uruchomieniu pliku pokazuje następujący wynik -
ans = The range for int8 is:
-128 to 127
ans = The range for int16 is:
-32768 to 32767
ans = The range for int32 is:
-2147483648 to 2147483647
ans = The range for int64 is:
0 to 0
ans = The range for uint8 is:
0 to 255
ans = The range for uint16 is:
0 to 65535
ans = The range for uint32 is:
0 to -1
ans = The range for uint64 is:
0 to 18446744073709551616Najmniejsze i największe liczby zmiennoprzecinkowe
Funkcje realmax() i realmin() zwracają maksymalne i minimalne wartości, które można przedstawić za pomocą liczb zmiennoprzecinkowych.
Obie funkcje wywołane z argumentem „single” zwracają maksymalne i minimalne wartości, które można przedstawić za pomocą typu danych o pojedynczej precyzji, a wywołanie z argumentem „double” zwracają maksymalne i minimalne wartości, które można przedstawić typ danych podwójnej precyzji.
Przykład
Poniższy przykład ilustruje, jak uzyskać najmniejsze i największe liczby zmiennoprzecinkowe. Utwórz plik skryptu i napisz w nim następujący kod -
% displaying the smallest and largest single-precision
% floating point number
str = 'The range for single is:\n\t%g to %g and\n\t %g to %g';
sprintf(str, -realmax('single'), -realmin('single'), ...
realmin('single'), realmax('single'))
% displaying the smallest and largest double-precision
% floating point number
str = 'The range for double is:\n\t%g to %g and\n\t %g to %g';
sprintf(str, -realmax('double'), -realmin('double'), ...
realmin('double'), realmax('double'))Po uruchomieniu pliku wyświetla następujący wynik -
ans = The range for single is:
-3.40282e+38 to -1.17549e-38 and
1.17549e-38 to 3.40282e+38
ans = The range for double is:
-1.79769e+308 to -2.22507e-308 and
2.22507e-308 to 1.79769e+308Tworzenie ciągu znaków w MATLAB-ie jest dość proste. W rzeczywistości używaliśmy go wiele razy. Na przykład wpisujesz w wierszu polecenia -
my_string = 'Tutorials Point'MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
my_string = Tutorials PointMATLAB traktuje wszystkie zmienne jako tablice, a ciągi znaków są traktowane jako tablice znaków. Użyjmywhos polecenie sprawdzenia zmiennej utworzonej powyżej -
whosMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
Name Size Bytes Class Attributes
my_string 1x16 32 charCo ciekawe, możesz użyć funkcji konwersji liczb, takich jak uint8 lub uint16aby przekonwertować znaki w ciągu na ich kody numeryczne. Plikchar funkcja konwertuje wektor liczb całkowitych z powrotem na znaki -
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
my_string = 'Tutorial''s Point';
str_ascii = uint8(my_string) % 8-bit ascii values
str_back_to_char= char(str_ascii)
str_16bit = uint16(my_string) % 16-bit ascii values
str_back_to_char = char(str_16bit)Po uruchomieniu pliku wyświetla następujący wynik -
str_ascii =
84 117 116 111 114 105 97 108 39 115 32 80 111 105 110 116
str_back_to_char = Tutorial's Point
str_16bit =
84 117 116 111 114 105 97 108 39 115 32 80 111 105 110 116
str_back_to_char = Tutorial's PointProstokątna tablica znaków
Ciągi, które omówiliśmy do tej pory, to jednowymiarowe tablice znaków; jednak musimy przechowywać więcej niż to. Musimy przechowywać bardziej wymiarowe dane tekstowe w naszym programie. Osiąga się to poprzez tworzenie prostokątnych tablic znaków.
Najprostszym sposobem tworzenia prostokątnej tablicy znaków jest konkatenacja dwóch lub więcej jednowymiarowych tablic znaków, w pionie lub w poziomie, zgodnie z wymaganiami.
Ciągi można łączyć w pionie na jeden z następujących sposobów -
Korzystanie z operatora konkatenacji MATLAB []i oddzielając każdy wiersz średnikiem (;). Należy pamiętać, że w tej metodzie każdy wiersz musi zawierać taką samą liczbę znaków. W przypadku ciągów o różnych długościach należy uzupełnić znaki spacjami w razie potrzeby.
Używając charfunkcjonować. Jeśli łańcuchy mają różne długości, krótsze ciągi znaków wypełnia spacjami końcowymi, tak aby każdy wiersz miał taką samą liczbę znaków.
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
doc_profile = ['Zara Ali '; ...
'Sr. Surgeon '; ...
'R N Tagore Cardiology Research Center']
doc_profile = char('Zara Ali', 'Sr. Surgeon', ...
'RN Tagore Cardiology Research Center')Po uruchomieniu pliku wyświetla następujący wynik -
doc_profile =
Zara Ali
Sr. Surgeon
R N Tagore Cardiology Research Center
doc_profile =
Zara Ali
Sr. Surgeon
RN Tagore Cardiology Research CenterCiągi można łączyć w poziomie na jeden z następujących sposobów -
Korzystając z operatora konkatenacji MATLAB, []i oddzielając ciągi wejściowe przecinkiem lub spacją. Ta metoda zachowuje wszelkie spacje końcowe w tablicach wejściowych.
Używając funkcji konkatenacji ciągów, strcat. Ta metoda usuwa końcowe spacje z danych wejściowych.
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
name = 'Zara Ali ';
position = 'Sr. Surgeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = [name ', ' position ', ' worksAt]
profile = strcat(name, ', ', position, ', ', worksAt)Po uruchomieniu pliku wyświetla następujący wynik -
profile = Zara Ali , Sr. Surgeon , R N Tagore Cardiology Research Center
profile = Zara Ali,Sr. Surgeon,R N Tagore Cardiology Research CenterŁączenie ciągów w tablicę komórek
Z naszej poprzedniej dyskusji jasno wynika, że łączenie ciągów o różnych długościach może być uciążliwe, ponieważ wszystkie ciągi w tablicy muszą mieć tę samą długość. Użyliśmy spacji na końcu ciągów, aby wyrównać ich długość.
Jednak bardziej wydajnym sposobem łączenia ciągów jest konwersja wynikowej tablicy na tablicę komórek.
Tablica komórek MATLAB może zawierać różne rozmiary i typy danych w tablicy. Macierze komórek zapewniają bardziej elastyczny sposób przechowywania ciągów o różnej długości.
Plik cellstr funkcja konwertuje tablicę znaków na tablicę komórek zawierającą ciągi.
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
name = 'Zara Ali ';
position = 'Sr. Surgeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = char(name, position, worksAt);
profile = cellstr(profile);
disp(profile)Po uruchomieniu pliku wyświetla następujący wynik -
{
[1,1] = Zara Ali
[2,1] = Sr. Surgeon
[3,1] = R N Tagore Cardiology Research Center
}Funkcje łańcuchowe w MATLAB
MATLAB zapewnia liczne funkcje ciągów do tworzenia, łączenia, analizowania, porównywania i manipulowania napisami.
Poniższa tabela zawiera krótki opis funkcji tekstowych w MATLAB -
| Funkcjonować | Cel, powód |
|---|---|
| Funkcje do przechowywania tekstu w tablicach znaków, łączenia tablic znaków itp. | |
| puste miejsca | Utwórz ciąg pustych znaków |
| cellstr | Utwórz tablicę komórek zawierającą ciągi znaków z tablicy znaków |
| zwęglać | Konwertuj na tablicę znaków (ciąg) |
| iscellstr | Określ, czy dane wejściowe to tablica komórek zawierająca ciągi |
| ischar | Określ, czy element jest tablicą znaków |
| sprintf | Sformatuj dane w ciąg |
| strcat | Połącz łańcuchy w poziomie |
| strjoin | Połącz ciągi w tablicy komórek w jeden ciąg |
| Funkcje do identyfikowania części ciągów, znajdowania i zastępowania podciągów | |
| ischar | Określ, czy element jest tablicą znaków |
| isletter | Elementy tablicy, które są literami alfabetu |
| isspace | Elementy tablicy, które są znakami spacji |
| isstrprop | Określ, czy ciąg należy do określonej kategorii |
| sscanf | Odczytaj sformatowane dane z ciągu |
| strfind | Znajdź jeden ciąg w innym |
| strrep | Znajdź i zamień podciąg |
| strsplit | Podziel ciąg na określonym separatorze |
| strtok | Wybrane części struny |
| validatestring | Sprawdź poprawność ciągu tekstowego |
| symvar | Określ zmienne symboliczne w wyrażeniu |
| regexp | Dopasuj wyrażenie regularne (z uwzględnieniem wielkości liter) |
| regexpi | Dopasuj wyrażenie regularne (bez rozróżniania wielkości liter) |
| regexprep | Zastąp ciąg przy użyciu wyrażenia regularnego |
| regexptranslate | Przetłumacz ciąg na wyrażenie regularne |
| Funkcje do porównywania ciągów | |
| strcmp | Porównaj ciągi (z uwzględnieniem wielkości liter) |
| strcmpi | Porównaj ciągi (bez rozróżniania wielkości liter) |
| strncmp | Porównaj pierwsze n znaków ciągów (z uwzględnieniem wielkości liter) |
| strncmpi | Porównaj pierwsze n znaków ciągów (bez rozróżniania wielkości liter) |
| Funkcje zmieniające łańcuch znaków na wielkie lub małe litery, tworzenie lub usuwanie białych znaków | |
| usuń puste | Usuń końcowe spacje z końca ciągu |
| strtrim | Usuń wiodące i końcowe białe znaki z ciągu |
| niższy | Konwertuj ciąg na małe litery |
| górny | Konwertuj ciąg na wielkie litery |
| strjust | Wyjustuj tablicę znaków |
Przykłady
Poniższe przykłady ilustrują niektóre z wyżej wymienionych funkcji tekstowych -
Ciągi formatujące
Utwórz plik skryptu i wpisz w nim następujący kod -
A = pi*1000*ones(1,5);
sprintf(' %f \n %.2f \n %+.2f \n %12.2f \n %012.2f \n', A)Po uruchomieniu pliku wyświetla następujący wynik -
ans = 3141.592654
3141.59
+3141.59
3141.59
000003141.59Łączenie ciągów
Utwórz plik skryptu i wpisz w nim następujący kod -
%cell array of strings
str_array = {'red','blue','green', 'yellow', 'orange'};
% Join strings in cell array into single string
str1 = strjoin(str_array, "-")
str2 = strjoin(str_array, ",")Po uruchomieniu pliku wyświetla następujący wynik -
str1 = red-blue-green-yellow-orange
str2 = red,blue,green,yellow,orangeZnajdowanie i zastępowanie ciągów
Utwórz plik skryptu i wpisz w nim następujący kod -
students = {'Zara Ali', 'Neha Bhatnagar', ...
'Monica Malik', 'Madhu Gautam', ...
'Madhu Sharma', 'Bhawna Sharma',...
'Nuha Ali', 'Reva Dutta', ...
'Sunaina Ali', 'Sofia Kabir'};
% The strrep function searches and replaces sub-string.
new_student = strrep(students(8), 'Reva', 'Poulomi')
% Display first names
first_names = strtok(students)Po uruchomieniu pliku wyświetla następujący wynik -
new_student =
{
[1,1] = Poulomi Dutta
}
first_names =
{
[1,1] = Zara
[1,2] = Neha
[1,3] = Monica
[1,4] = Madhu
[1,5] = Madhu
[1,6] = Bhawna
[1,7] = Nuha
[1,8] = Reva
[1,9] = Sunaina
[1,10] = Sofia
}Porównywanie ciągów
Utwórz plik skryptu i wpisz w nim następujący kod -
str1 = 'This is test'
str2 = 'This is text'
if (strcmp(str1, str2))
sprintf('%s and %s are equal', str1, str2)
else
sprintf('%s and %s are not equal', str1, str2)
endPo uruchomieniu pliku wyświetla następujący wynik -
str1 = This is test
str2 = This is text
ans = This is test and This is text are not equalFunkcja to grupa instrukcji, które razem wykonują zadanie. W MATLAB-ie funkcje są definiowane w oddzielnych plikach. Nazwa pliku i funkcji powinny być takie same.
Funkcje działają na zmiennych w ich własnym obszarze roboczym, który jest również nazywany local workspace, niezależnie od obszaru roboczego, do którego uzyskujesz dostęp z wiersza polecenia MATLAB, który jest nazywany base workspace.
Funkcje mogą akceptować więcej niż jeden argument wejściowy i mogą zwracać więcej niż jeden argument wyjściowy.
Składnia instrukcji funkcji to -
function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)Przykład
Następującą funkcję o nazwie mymax należy zapisać w pliku o nazwie mymax.m . Przyjmuje pięć liczb jako argument i zwraca ich maksimum.
Utwórz plik funkcji o nazwie mymax.m i wpisz w nim następujący kod -
function max = mymax(n1, n2, n3, n4, n5)
%This function calculates the maximum of the
% five numbers given as input
max = n1;
if(n2 > max)
max = n2;
end
if(n3 > max)
max = n3;
end
if(n4 > max)
max = n4;
end
if(n5 > max)
max = n5;
endPierwsza linia funkcji zaczyna się od słowa kluczowego function. Podaje nazwę funkcji i kolejność argumentów. W naszym przykładzie funkcja mymax ma pięć argumentów wejściowych i jeden argument wyjściowy.
Wiersze komentarza, które znajdują się bezpośrednio po instrukcji funkcyjnej, zawierają tekst pomocy. Te wiersze są drukowane podczas wpisywania -
help mymaxMATLAB wykona powyższą instrukcję i zwróci następujący wynik -
This function calculates the maximum of the
five numbers given as inputMożesz wywołać funkcję jako -
mymax(34, 78, 89, 23, 11)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans = 89Funkcje anonimowe
Funkcja anonimowa jest podobna do funkcji wbudowanej w tradycyjnych językach programowania, zdefiniowanej w pojedynczej instrukcji MATLAB. Składa się z pojedynczego wyrażenia MATLAB oraz dowolnej liczby argumentów wejściowych i wyjściowych.
Możesz zdefiniować anonimową funkcję bezpośrednio w wierszu poleceń MATLAB lub w funkcji lub skrypcie.
W ten sposób możesz tworzyć proste funkcje bez konieczności tworzenia dla nich pliku.
Składnia tworzenia anonimowej funkcji na podstawie wyrażenia to
f = @(arglist)expressionPrzykład
W tym przykładzie napiszemy anonimową funkcję o nazwie power, która przyjmie dwie liczby jako dane wejściowe i zwróci pierwszą liczbę podniesioną do potęgi drugiej liczby.
Utwórz plik skryptu i wpisz w nim następujący kod -
power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)Po uruchomieniu pliku wyświetla się -
result1 = 343
result2 = 7
result3 = 1.0000e-10
result4 = 9.5459Funkcje podstawowe i podrzędne
Każda funkcja inna niż funkcja anonimowa musi być zdefiniowana w pliku. Każdy plik funkcji zawiera wymaganą funkcję podstawową, która pojawia się jako pierwsza, oraz dowolną liczbę opcjonalnych funkcji podrzędnych, które występują po funkcji podstawowej i są przez nią używane.
Funkcje podstawowe mogą być wywoływane spoza pliku, który je definiuje, z wiersza poleceń lub z innych funkcji, ale funkcje podrzędne nie mogą być wywoływane z wiersza poleceń lub innych funkcji, poza plikiem funkcji.
Funkcje podrzędne są widoczne tylko dla funkcji podstawowej i innych funkcji podrzędnych w pliku funkcji, który je definiuje.
Przykład
Napiszmy funkcję o nazwie kwadratowa, która obliczyłaby pierwiastki równania kwadratowego. Funkcja wymagałaby trzech wejść, współczynnika kwadratowego, współczynnika liniowego i stałego członu. Przywróciłoby korzenie.
Plik funkcji quadratic.m będzie zawierał podstawową funkcję kwadratową i dysk podrzędny , który oblicza dyskryminację.
Utwórz plik funkcji quadratic.m i wpisz w nim następujący kod -
function [x1,x2] = quadratic(a,b,c)
%this function returns the roots of
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficients of x2, x and the
%constant term
% It returns the roots
d = disc(a,b,c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic
function dis = disc(a,b,c)
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-functionMożesz wywołać powyższą funkcję z wiersza polecenia jako -
quadratic(2,4,-4)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans = 0.7321Funkcje zagnieżdżone
Możesz zdefiniować funkcje w treści innej funkcji. Nazywa się to funkcjami zagnieżdżonymi. Zagnieżdżona funkcja zawiera dowolny lub wszystkie składniki dowolnej innej funkcji.
Funkcje zagnieżdżone są zdefiniowane w zakresie innej funkcji i współdzielą dostęp do obszaru roboczego funkcji zawierającej.
Zagnieżdżona funkcja ma następującą składnię -
function x = A(p1, p2)
...
B(p2)
function y = B(p3)
...
end
...
endPrzykład
Przepiszmy funkcję kwadratową , z poprzedniego przykładu, jednak tym razem funkcja dysku będzie funkcją zagnieżdżoną.
Utwórz plik funkcji quadratic2.m i wpisz w nim następujący kod -
function [x1,x2] = quadratic2(a,b,c)
function disc % nested function
d = sqrt(b^2 - 4*a*c);
end % end of function disc
disc;
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of function quadratic2Możesz wywołać powyższą funkcję z wiersza polecenia jako -
quadratic2(2,4,-4)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans = 0.73205Funkcje prywatne
Funkcja prywatna to funkcja podstawowa, która jest widoczna tylko dla ograniczonej grupy innych funkcji. Jeśli nie chcesz ujawniać implementacji funkcji, możesz je utworzyć jako funkcje prywatne.
Funkcje prywatne znajdują się w subfolders ze specjalną nazwą private.
Są widoczne tylko dla funkcji w folderze nadrzędnym.
Przykład
Pozwól nam przepisać kwadratową funkcję. Tym razem jednak funkcja dysku obliczająca dyskryminację będzie funkcją prywatną.
Utwórz podfolder o nazwie private w katalogu roboczym. Zapisz w nim następujący plik funkcji disc.m -
function dis = disc(a,b,c)
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-functionUtwórz funkcję quadratic3.m w katalogu roboczym i wpisz w niej następujący kod -
function [x1,x2] = quadratic3(a,b,c)
%this function returns the roots of
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficient of x2, x and the
%constant term
% It returns the roots
d = disc(a,b,c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic3Możesz wywołać powyższą funkcję z wiersza polecenia jako -
quadratic3(2,4,-4)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans = 0.73205Zmienne globalne
Zmienne globalne mogą być współużytkowane przez więcej niż jedną funkcję. W tym celu musisz zadeklarować zmienną jako globalną we wszystkich funkcjach.
Jeśli chcesz uzyskać dostęp do tej zmiennej z podstawowego obszaru roboczego, zadeklaruj zmienną w wierszu poleceń.
Deklaracja globalna musi wystąpić, zanim zmienna zostanie faktycznie użyta w funkcji. Dobrą praktyką jest używanie wielkich liter w nazwach zmiennych globalnych, aby odróżnić je od innych zmiennych.
Przykład
Utwórzmy plik funkcji o nazwie Average.m i wpisz w nim następujący kod -
function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
endUtwórz plik skryptu i wpisz w nim następujący kod -
global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)Po uruchomieniu pliku wyświetli się następujący wynik -
av = 35.500Importowanie danych do MATLABA oznacza ładowanie danych z zewnętrznego pliku. Plikimportdatafunkcja umożliwia ładowanie różnych plików danych w różnych formatach. Ma pięć następujących form -
| Sr.No. | Opis funkcji |
|---|---|
| 1 | A = importdata(filename) Ładuje dane do tablicy A z pliku oznaczonego nazwą pliku . |
| 2 | A = importdata('-pastespecial') Ładuje dane ze schowka systemowego, a nie z pliku. |
| 3 | A = importdata(___, delimiterIn) Interpretuje delimiterIn jako separator kolumn w pliku ASCII, nazwie pliku lub danych ze schowka. Możesz użyć delimiterIn z dowolnym argumentem wejściowym w powyższych składniach. |
| 4 | A = importdata(___, delimiterIn, headerlinesIn) Wczytuje dane z pliku ASCII, nazwy pliku lub schowka, odczytując dane numeryczne zaczynając od nagłówków linii w + 1 . |
| 5 | [A, delimiterOut, headerlinesOut] = importdata(___) Zwraca wykryty znak separatora dla wejściowego pliku ASCII w parametrze delimiterOut i wykrytą liczbę wierszy nagłówka w nagłówku headerOut , używając dowolnego argumentu wejściowego z poprzedniej składni. |
Domyślnie Octave nie obsługuje funkcji importdata () , więc będziesz musiał wyszukać i zainstalować ten pakiet, aby następujące przykłady działały z Twoją instalacją Octave.
Przykład 1
Załadujmy i wyświetlmy plik obrazu. Utwórz plik skryptu i wpisz w nim następujący kod -
filename = 'smile.jpg';
A = importdata(filename);
image(A);Po uruchomieniu pliku MATLAB wyświetla plik obrazu. Musisz jednak przechowywać go w bieżącym katalogu.

Przykład 2
W tym przykładzie importujemy plik tekstowy i określamy ogranicznik i nagłówek kolumny. Utwórzmy plik ASCII rozdzielany spacjami z nagłówkami kolumn, nazwany weekdata.txt .
Nasz plik tekstowy weekdata.txt wygląda następująco -
SunDay MonDay TuesDay WednesDay ThursDay FriDay SaturDay
95.01 76.21 61.54 40.57 55.79 70.28 81.53
73.11 45.65 79.19 93.55 75.29 69.87 74.68
60.68 41.85 92.18 91.69 81.32 90.38 74.51
48.60 82.14 73.82 41.03 0.99 67.22 93.18
89.13 44.47 57.63 89.36 13.89 19.88 46.60Utwórz plik skryptu i wpisz w nim następujący kod -
filename = 'weeklydata.txt';
delimiterIn = ' ';
headerlinesIn = 1;
A = importdata(filename,delimiterIn,headerlinesIn);
% View data
for k = [1:7]
disp(A.colheaders{1, k})
disp(A.data(:, k))
disp(' ')
endPo uruchomieniu pliku wyświetla następujący wynik -
SunDay
95.0100
73.1100
60.6800
48.6000
89.1300
MonDay
76.2100
45.6500
41.8500
82.1400
44.4700
TuesDay
61.5400
79.1900
92.1800
73.8200
57.6300
WednesDay
40.5700
93.5500
91.6900
41.0300
89.3600
ThursDay
55.7900
75.2900
81.3200
0.9900
13.8900
FriDay
70.2800
69.8700
90.3800
67.2200
19.8800
SaturDay
81.5300
74.6800
74.5100
93.1800
46.6000Przykład 3
W tym przykładzie zaimportujmy dane ze schowka.
Skopiuj następujące wiersze do schowka -
Mathematics is simple
Utwórz plik skryptu i wpisz następujący kod -
A = importdata('-pastespecial')Po uruchomieniu pliku wyświetla następujący wynik -
A =
'Mathematics is simple'We / wy niskiego poziomu pliku
Funkcja importdata jest funkcją wysokiego poziomu. Niskopoziomowe funkcje wejścia / wyjścia pliku w MATLAB-u zapewniają największą kontrolę nad odczytem lub zapisem danych do pliku. Jednak te funkcje wymagają bardziej szczegółowych informacji o pliku, aby działać wydajnie.
MATLAB zapewnia następujące funkcje do operacji odczytu i zapisu na poziomie bajtów lub znaków -
| Funkcjonować | Opis |
|---|---|
| fclose | Zamknij jeden lub wszystkie otwarte pliki |
| feof | Przetestuj pod kątem końca pliku |
| Ferror | Informacje o błędach we / wy pliku |
| fgetl | Czytaj linię z pliku, usuwając znaki nowej linii |
| fgets | Odczytaj wiersz z pliku, zachowując znaki nowego wiersza |
| fopen | Otwórz plik lub uzyskaj informacje o otwartych plikach |
| fprintf | Zapisz dane do pliku tekstowego |
| fread | Odczytaj dane z pliku binarnego |
| Frewind | Przenieś wskaźnik pozycji pliku na początek otwartego pliku |
| fscanf | Odczytaj dane z pliku tekstowego |
| fseek | Przejdź do określonej pozycji w pliku |
| ftell | Pozycja w otwartym pliku |
| fwrite | Zapisz dane do pliku binarnego |
Importuj pliki danych tekstowych z niskopoziomowymi we / wy
MATLAB zapewnia następujące funkcje do niskopoziomowego importu plików danych tekstowych -
Plik fscanf funkcja odczytuje sformatowane dane w pliku tekstowym lub ASCII.
Plik fgetl i fgets funkcje odczytują jeden wiersz pliku na raz, gdzie znak nowego wiersza oddziela każdy wiersz.
Plik fread funkcja odczytuje strumień danych na poziomie bajtów lub bitów.
Przykład
Mamy plik danych tekstowych „myfile.txt” zapisany w naszym katalogu roboczym. Plik przechowuje dane dotyczące opadów przez trzy miesiące; Czerwiec, lipiec i sierpień za rok 2012.
Dane w myfile.txt zawierają powtarzające się zestawy pomiarów czasu, miesiąca i opadów w pięciu miejscach. Dane nagłówka przechowują liczbę miesięcy M; więc mamy M zestawów pomiarów.
Plik wygląda następująco -
Rainfall Data
Months: June, July, August
M = 3
12:00:00
June-2012
17.21 28.52 39.78 16.55 23.67
19.15 0.35 17.57 NaN 12.01
17.92 28.49 17.40 17.06 11.09
9.59 9.33 NaN 0.31 0.23
10.46 13.17 NaN 14.89 19.33
20.97 19.50 17.65 14.45 14.00
18.23 10.34 17.95 16.46 19.34
09:10:02
July-2012
12.76 16.94 14.38 11.86 16.89
20.46 23.17 NaN 24.89 19.33
30.97 49.50 47.65 24.45 34.00
18.23 30.34 27.95 16.46 19.34
30.46 33.17 NaN 34.89 29.33
30.97 49.50 47.65 24.45 34.00
28.67 30.34 27.95 36.46 29.34
15:03:40
August-2012
17.09 16.55 19.59 17.25 19.22
17.54 11.45 13.48 22.55 24.01
NaN 21.19 25.85 25.05 27.21
26.79 24.98 12.23 16.99 18.67
17.54 11.45 13.48 22.55 24.01
NaN 21.19 25.85 25.05 27.21
26.79 24.98 12.23 16.99 18.67Zaimportujemy dane z tego pliku i wyświetlimy te dane. Wykonaj następujące kroki -
Otwórz plik za pomocą fopen funkcji i pobierz identyfikator pliku.
Opisz dane w pliku za pomocą format specifiers, Jak na przykład '%s'na string',%d'dla liczby całkowitej lub'%f'dla liczby zmiennoprzecinkowej.
Aby pominąć znaki literału w pliku, umieść je w opisie formatu. Aby pominąć pole danych, użyj gwiazdki („*”) w specyfikatorze.
Na przykład, aby odczytać nagłówki i zwrócić pojedynczą wartość dla M, piszemy -
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);Domyślnie, fscanfczyta dane zgodnie z naszym opisem formatu, dopóki nie znajdzie żadnego dopasowania dla danych lub nie osiągnie końca pliku. Tutaj użyjemy pętli for do odczytu 3 zestawów danych i za każdym razem odczyta 7 wierszy i 5 kolumn.
W obszarze roboczym utworzymy strukturę o nazwie mydata do przechowywania danych odczytanych z pliku. Ta struktura ma trzy pola - tablicę czasu , miesiąca i danych deszczowych .
Utwórz plik skryptu i wpisz w nim następujący kod -
filename = '/data/myfile.txt';
rows = 7;
cols = 5;
% open the file
fid = fopen(filename);
% read the file headers, find M (number of months)
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);
% read each set of measurements
for n = 1:M
mydata(n).time = fscanf(fid, '%s', 1);
mydata(n).month = fscanf(fid, '%s', 1);
% fscanf fills the array in column order,
% so transpose the results
mydata(n).raindata = ...
fscanf(fid, '%f', [rows, cols]);
end
for n = 1:M
disp(mydata(n).time), disp(mydata(n).month)
disp(mydata(n).raindata)
end
% close the file
fclose(fid);Po uruchomieniu pliku wyświetla następujący wynik -
12:00:00
June-2012
17.2100 17.5700 11.0900 13.1700 14.4500
28.5200 NaN 9.5900 NaN 14.0000
39.7800 12.0100 9.3300 14.8900 18.2300
16.5500 17.9200 NaN 19.3300 10.3400
23.6700 28.4900 0.3100 20.9700 17.9500
19.1500 17.4000 0.2300 19.5000 16.4600
0.3500 17.0600 10.4600 17.6500 19.3400
09:10:02
July-2012
12.7600 NaN 34.0000 33.1700 24.4500
16.9400 24.8900 18.2300 NaN 34.0000
14.3800 19.3300 30.3400 34.8900 28.6700
11.8600 30.9700 27.9500 29.3300 30.3400
16.8900 49.5000 16.4600 30.9700 27.9500
20.4600 47.6500 19.3400 49.5000 36.4600
23.1700 24.4500 30.4600 47.6500 29.3400
15:03:40
August-2012
17.0900 13.4800 27.2100 11.4500 25.0500
16.5500 22.5500 26.7900 13.4800 27.2100
19.5900 24.0100 24.9800 22.5500 26.7900
17.2500 NaN 12.2300 24.0100 24.9800
19.2200 21.1900 16.9900 NaN 12.2300
17.5400 25.8500 18.6700 21.1900 16.9900
11.4500 25.0500 17.5400 25.8500 18.6700Eksport danych (lub wyjście) w MATLAB-ie oznacza zapis do plików. MATLAB pozwala na wykorzystanie Twoich danych w innej aplikacji, która czyta pliki ASCII. W tym celu MATLAB udostępnia kilka opcji eksportu danych.
Możesz tworzyć następujące typy plików -
Prostokątny, rozdzielany plik danych ASCII z tablicy.
Plik dziennika (lub dziennika) naciśnięć klawiszy i wynikowego tekstu wyjściowego.
Specjalistyczny plik ASCII wykorzystujący funkcje niskiego poziomu, takie jak fprintf.
Plik MEX, aby uzyskać dostęp do procedury C / C ++ lub Fortran, która zapisuje w określonym formacie pliku tekstowego.
Oprócz tego możesz również eksportować dane do arkuszy kalkulacyjnych.
Istnieją dwa sposoby wyeksportowania tablicy liczbowej jako pliku danych ASCII z separatorami -
Używając save funkcji i określając -ascii kwalifikator
Używając dlmwrite funkcjonować
Składnia użycia funkcji zapisywania to -
save my_data.out num_array -asciigdzie my_data.out to utworzony plik danych ASCII z wartościami rozdzielanymi, num_array to tablica numeryczna, a−ascii jest specyfikatorem.
Składnia korzystania z dlmwrite funkcja jest -
dlmwrite('my_data.out', num_array, 'dlm_char')gdzie my_data.out to utworzony plik danych ASCII z wartościami rozdzielanymi, num_array to tablica numeryczna, a dlm_char to znak separatora.
Przykład
Poniższy przykład ilustruje koncepcję. Utwórz plik skryptu i wpisz następujący kod -
num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ascii;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.outPo uruchomieniu pliku wyświetla następujący wynik -
1.0000000e+00 2.0000000e+00 3.0000000e+00 4.0000000e+00
4.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00
7.0000000e+00 8.0000000e+00 9.0000000e+00 0.0000000e+00
1 2 3 4
4 5 6 7
7 8 9 0Należy pamiętać, że polecenie save -ascii i funkcja dlmwrite nie działają z tablicami komórek jako danymi wejściowymi. Aby utworzyć rozdzielany plik ASCII z zawartości tablicy komórek, możesz
Albo przekonwertuj tablicę komórek na macierz przy użyciu cell2mat funkcjonować
Lub wyeksportuj tablicę komórek przy użyciu niskopoziomowych funkcji wejścia / wyjścia pliku.
Jeśli używasz save funkcja zapisująca tablicę znaków do pliku ASCII, zapisuje odpowiednik znaków ASCII w pliku.
Na przykład napiszmy słowo „cześć” do pliku -
h = 'hello';
save textdata.out h -ascii
type textdata.outMATLAB wykonuje powyższe instrukcje i wyświetla następujący wynik. czyli znaki łańcucha „cześć” w 8-cyfrowym formacie ASCII.
1.0400000e+02 1.0100000e+02 1.0800000e+02 1.0800000e+02 1.1100000e+02Pisanie do plików dziennika
Pliki dziennika to dzienniki aktywności Twojej sesji MATLAB. Funkcja dziennika tworzy dokładną kopię sesji w pliku dyskowym, z wyłączeniem grafiki.
Aby włączyć funkcję dziennika, wpisz -
diaryOpcjonalnie możesz podać nazwę pliku dziennika, powiedzmy -
diary logdata.outAby wyłączyć funkcję dziennika -
diary offMożesz otworzyć plik dziennika w edytorze tekstu.
Eksportowanie danych do plików danych tekstowych z niskopoziomowymi wejściami / wyjściami
Do tej pory wyeksportowaliśmy tablice numeryczne. Jednak może być konieczne utworzenie innych plików tekstowych, w tym kombinacji danych liczbowych i znakowych, nieprostokątnych plików wyjściowych lub plików z kodowaniem innym niż ASCII. W tym celu MATLAB zapewnia niski poziomfprintf funkcjonować.
Podobnie jak w przypadku niskopoziomowych działań związanych z plikami we / wy, przed eksportowaniem należy otworzyć lub utworzyć plik z rozszerzeniem fopenfunkcji i pobierz identyfikator pliku. Domyślnie fopen otwiera plik w trybie tylko do odczytu. Powinieneś określić uprawnienia do zapisu lub dołączania, takie jak „w” lub „a”.
Po przetworzeniu pliku musisz go zamknąć za pomocą fclose(fid) funkcjonować.
Poniższy przykład ilustruje koncepcję -
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
% create a matrix y, with two rows
x = 0:10:100;
y = [x; log(x)];
% open a file for writing
fid = fopen('logtable.txt', 'w');
% Table Header
fprintf(fid, 'Log Function\n\n');
% print values in column order
% two values appear on each row of the file
fprintf(fid, '%f %f\n', y);
fclose(fid);
% display the file created
type logtable.txtPo uruchomieniu pliku wyświetla następujący wynik -
Log Function
0.000000 -Inf
10.000000 2.302585
20.000000 2.995732
30.000000 3.401197
40.000000 3.688879
50.000000 3.912023
60.000000 4.094345
70.000000 4.248495
80.000000 4.382027
90.000000 4.499810
100.000000 4.605170Aby wykreślić wykres funkcji, musisz wykonać następujące czynności -
Definiować x, określając range of values dla zmiennej x, dla którego ma zostać naniesiona funkcja
Zdefiniuj funkcję, y = f(x)
Zadzwoń do plot polecenie, jak plot(x, y)
Poniższy przykład zademonstruje koncepcję. Wykreślmy prostą funkcjęy = x dla zakresu wartości x od 0 do 100, z przyrostem o 5.
Utwórz plik skryptu i wpisz następujący kod -
x = [0:5:100];
y = x;
plot(x, y)Po uruchomieniu pliku MATLAB wyświetla następujący wykres -

Weźmy jeszcze jeden przykład, aby wykreślić funkcję y = x 2 . W tym przykładzie narysujemy dwa wykresy z tą samą funkcją, ale za drugim razem zmniejszymy wartość przyrostu. Zwróć uwagę, że gdy zmniejszamy przyrost, wykres staje się gładszy.
Utwórz plik skryptu i wpisz następujący kod -
x = [1 2 3 4 5 6 7 8 9 10];
x = [-100:20:100];
y = x.^2;
plot(x, y)Po uruchomieniu pliku MATLAB wyświetla następujący wykres -
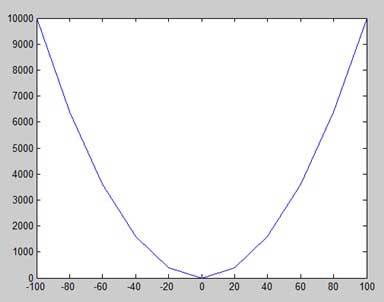
Zmień trochę plik kodu, zmniejsz przyrost do 5 -
x = [-100:5:100];
y = x.^2;
plot(x, y)MATLAB rysuje płynniejszy wykres -
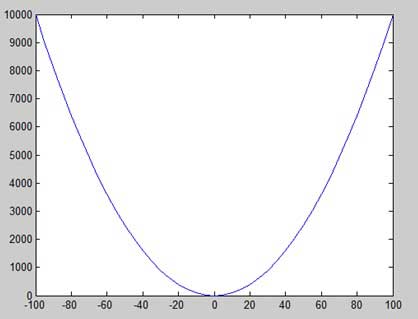
Dodawanie tytułu, etykiet, linii siatki i skalowania na wykresie
MATLAB pozwala na dodawanie tytułów, etykiet wzdłuż osi X i Y, linii siatki, a także dostosowywanie osi, aby uwydatnić wykres.
Plik xlabel i ylabel polecenia generują etykiety wzdłuż osi X i Y.
Plik title Polecenie pozwala na umieszczenie tytułu na wykresie.
Plik grid on Polecenie pozwala na umieszczenie linii siatki na wykresie.
Plik axis equal Polecenie pozwala na wygenerowanie wykresu z tymi samymi współczynnikami skali i przestrzeniami na obu osiach.
Plik axis square polecenie generuje kwadratowy wykres.
Przykład
Utwórz plik skryptu i wpisz następujący kod -
x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'),
grid on, axis equalMATLAB generuje następujący wykres -
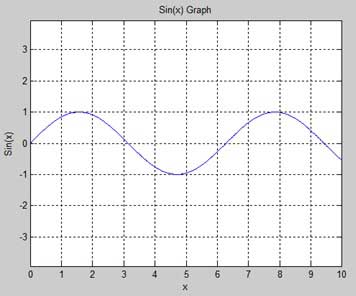
Rysowanie wielu funkcji na tym samym wykresie
Możesz narysować wiele wykresów na tym samym wykresie. Poniższy przykład ilustruje koncepcję -
Przykład
Utwórz plik skryptu i wpisz następujący kod -
x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')MATLAB generuje następujący wykres -
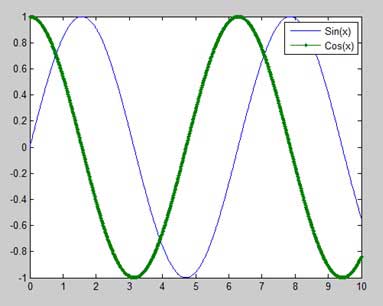
Ustawianie kolorów na wykresie
MATLAB zapewnia osiem podstawowych opcji kolorów do rysowania wykresów. Poniższa tabela przedstawia kolory i ich kody -
| Kod | Kolor |
|---|---|
| w | Biały |
| k | czarny |
| b | niebieski |
| r | Czerwony |
| do | Cyjan |
| sol | Zielony |
| m | Magenta |
| y | Żółty |
Przykład
Narysujmy wykres dwóch wielomianów
f (x) = 3x 4 + 2x 3 + 7x 2 + 2x + 9 i
g (x) = 5x 3 + 9x + 2
Utwórz plik skryptu i wpisz następujący kod -
x = [-10 : 0.01: 10];
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
plot(x, y, 'r', x, g, 'g')Po uruchomieniu pliku MATLAB generuje następujący wykres -
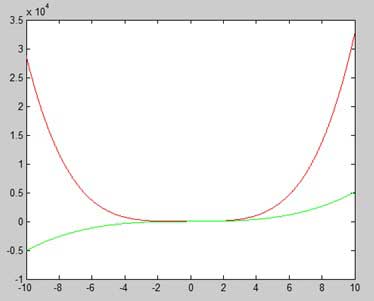
Ustawianie skali osi
Plik axisPolecenie pozwala ustawić skale osi. Możesz podać minimalne i maksymalne wartości dla osi X i Y za pomocą polecenia osi w następujący sposób -
axis ( [xmin xmax ymin ymax] )Poniższy przykład pokazuje to -
Przykład
Utwórz plik skryptu i wpisz następujący kod -
x = [0 : 0.01: 10];
y = exp(-x).* sin(2*x + 3);
plot(x, y), axis([0 10 -1 1])Po uruchomieniu pliku MATLAB generuje następujący wykres -
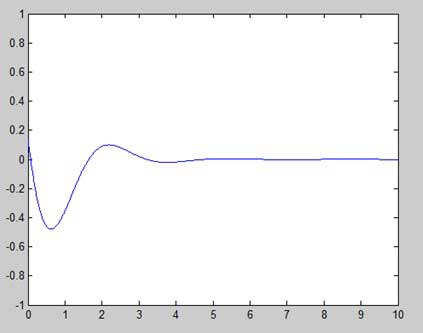
Generowanie działek podrzędnych
Kiedy tworzysz tablicę wykresów na tej samej figurze, każdy z tych wykresów nazywany jest wykresem podrzędnym. Pliksubplot polecenie służy do tworzenia wykresów podrzędnych.
Składnia polecenia to -
subplot(m, n, p)gdzie, m i n to liczba wierszy i kolumn tablicy plot, a p określa, gdzie umieścić dany wykres.
Każdy wykres utworzony za pomocą polecenia Subplot może mieć swoją własną charakterystykę. Poniższy przykład ilustruje koncepcję -
Przykład
Wygenerujmy dwa wykresy -
y = e −1,5x sin (10x)
y = e −2x sin (10x)
Utwórz plik skryptu i wpisz następujący kod -
x = [0:0.01:5];
y = exp(-1.5*x).*sin(10*x);
subplot(1,2,1)
plot(x,y), xlabel('x'),ylabel('exp(–1.5x)*sin(10x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(10*x);
subplot(1,2,2)
plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(10x)'),axis([0 5 -1 1])Po uruchomieniu pliku MATLAB generuje następujący wykres -
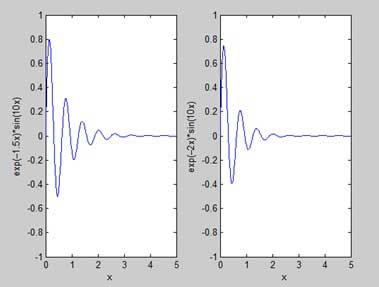
W tym rozdziale będziemy kontynuować badanie możliwości kreślenia i grafiki MATLAB-a. Omówimy -
- Rysowanie wykresów słupkowych
- Rysowanie konturów
- Działki trójwymiarowe
Rysowanie wykresów słupkowych
Plik barpolecenie rysuje dwuwymiarowy wykres słupkowy. Podajmy przykład, aby zademonstrować pomysł.
Przykład
Stwórzmy wyimaginowaną klasę z 10 studentami. Wiemy, że procent ocen uzyskanych przez tych uczniów to 75, 58, 90, 87, 50, 85, 92, 75, 60 i 95. Narysujemy wykres słupkowy dla tych danych.
Utwórz plik skryptu i wpisz następujący kod -
x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.epsPo uruchomieniu pliku MATLAB wyświetla następujący wykres słupkowy -

Rysowanie konturów
Warstwica funkcji dwóch zmiennych jest krzywą, wzdłuż której funkcja ma stałą wartość. Warstwice służą do tworzenia map konturowych poprzez łączenie punktów o równej wysokości nad określonym poziomem, np. Średnim poziomem morza.
MATLAB zapewnia contour funkcja do rysowania map konturowych.
Przykład
Wygenerujmy mapę konturową pokazującą warstwice dla danej funkcji g = f (x, y). Ta funkcja ma dwie zmienne. Będziemy więc musieli wygenerować dwie zmienne niezależne, tj. Dwa zbiory danych x i y. Odbywa się to przez wywołaniemeshgrid Komenda.
Plik meshgrid Polecenie służy do generowania macierzy elementów podających zakres po x i y wraz z określeniem przyrostu w każdym przypadku.
Wykreślmy naszą funkcję g = f (x, y), gdzie −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Przyjmijmy przyrost o 0,1 dla obu wartości. Zmienne są ustawione jako -
[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);Na koniec musimy przypisać funkcję. Niech naszą funkcją będzie: x 2 + y 2
Utwórz plik skryptu i wpisz następujący kod -
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables
g = x.^2 + y.^2; % our function
contour(x,y,g) % call the contour function
print -deps graph.epsPo uruchomieniu pliku MATLAB wyświetla następującą mapę konturową -
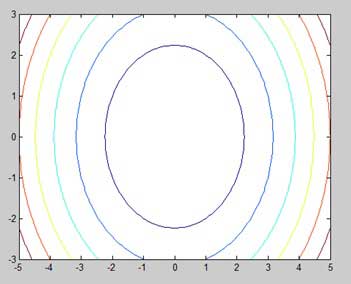
Zmodyfikujmy trochę kod, aby uatrakcyjnić mapę
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables
g = x.^2 + y.^2; % our function
[C, h] = contour(x,y,g); % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.epsPo uruchomieniu pliku MATLAB wyświetla następującą mapę konturową -
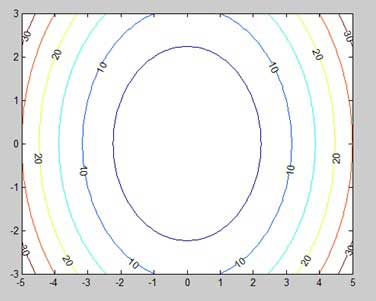
Działki trójwymiarowe
Wykresy trójwymiarowe zasadniczo przedstawiają powierzchnię zdefiniowaną przez funkcję w dwóch zmiennych, g = f (x, y).
Jak poprzednio, aby zdefiniować g, najpierw tworzymy zbiór (x, y) punktów w dziedzinie funkcji za pomocą meshgridKomenda. Następnie przypisujemy samą funkcję. Na koniec używamysurf polecenie, aby utworzyć wykres powierzchni.
Poniższy przykład ilustruje koncepcję -
Przykład
Stwórzmy trójwymiarową mapę powierzchni dla funkcji g = xe - (x 2 + y 2 )
Utwórz plik skryptu i wpisz następujący kod -
[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.epsPo uruchomieniu pliku MATLAB wyświetla następującą mapę 3-W -

Możesz także użyć meshpolecenie, aby wygenerować trójwymiarową powierzchnię. Jednakżesurf polecenie wyświetla zarówno linie łączące, jak i ściany powierzchni w kolorze, podczas gdy mesh polecenie tworzy powierzchnię szkieletową z kolorowymi liniami łączącymi definiujące punkty.
Jak dotąd widzieliśmy, że wszystkie przykłady działają w MATLAB-ie, a także w GNU, alternatywnie nazywanym Octave. Ale jeśli chodzi o rozwiązywanie podstawowych równań algebraicznych, zarówno MATLAB, jak i Octave są trochę inne, więc spróbujemy omówić MATLAB i Octave w osobnych sekcjach.
Omówimy także faktoryzację i upraszczanie wyrażeń algebraicznych.
Rozwiązywanie podstawowych równań algebraicznych w MATLAB
Plik solveFunkcja służy do rozwiązywania równań algebraicznych. W najprostszej postaci funkcja rozwiązywania przyjmuje jako argument równanie ujęte w cudzysłów.
Na przykład, rozwiążmy dla x w równaniu x-5 = 0
solve('x-5=0')MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
5Możesz również wywołać funkcję rozwiązywania jako -
y = solve('x-5 = 0')MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
y =
5Możesz nawet nie uwzględnić prawej strony równania -
solve('x-5')MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
5Jeśli równanie obejmuje wiele symboli, MATLAB domyślnie zakłada, że rozwiązujesz dla x, jednak funkcja rozwiązywania ma inną postać -
solve(equation, variable)gdzie możesz również wspomnieć o zmiennej.
Na przykład rozwiążmy równanie v - u - 3t 2 = 0, dla v.W takim przypadku powinniśmy napisać -
solve('v-u-3*t^2=0', 'v')MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
3*t^2 + uRozwiązywanie podstawowych równań algebraicznych w oktawie
Plik roots Funkcja służy do rozwiązywania równań algebraicznych w oktawie i możesz napisać powyższe przykłady w następujący sposób -
Na przykład, rozwiążmy dla x w równaniu x-5 = 0
roots([1, -5])Octave wykona powyższą instrukcję i zwróci następujący wynik -
ans = 5Możesz również wywołać funkcję rozwiązywania jako -
y = roots([1, -5])Octave wykona powyższą instrukcję i zwróci następujący wynik -
y = 5Rozwiązywanie równań kwadratowych w MATLAB
Plik solvefunkcja może również rozwiązywać równania wyższego rzędu. Jest często używany do rozwiązywania równań kwadratowych. Funkcja zwraca pierwiastki równania w tablicy.
Poniższy przykład rozwiązuje równanie kwadratowe x 2 -7x +12 = 0. Utwórz plik skryptu i wpisz następujący kod -
eq = 'x^2 -7*x + 12 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));Po uruchomieniu pliku wyświetla następujący wynik -
The first root is:
3
The second root is:
4Rozwiązywanie równań kwadratowych w oktawie
Poniższy przykład rozwiązuje równanie kwadratowe x 2 -7x +12 = 0 w oktawie. Utwórz plik skryptu i wpisz następujący kod -
s = roots([1, -7, 12]);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));Po uruchomieniu pliku wyświetla następujący wynik -
The first root is:
4
The second root is:
3Rozwiązywanie równań wyższego rzędu w MATLAB
Plik solvefunkcja może również rozwiązywać równania wyższego rzędu. Na przykład rozwiążmy równanie sześcienne jako (x-3) 2 (x-7) = 0
solve('(x-3)^2*(x-7)=0')MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
3
3
7W przypadku równań wyższego rzędu pierwiastki są długie i zawierają wiele terminów. Wartość liczbową takich pierwiastków można uzyskać, zamieniając je na podwójne. Poniższy przykład rozwiązuje równanie czwartego rzędu x 4 - 7x 3 + 3x 2 - 5x + 9 = 0.
Utwórz plik skryptu i wpisz następujący kod -
eq = 'x^4 - 7*x^3 + 3*x^2 - 5*x + 9 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
disp('The third root is: '), disp(s(3));
disp('The fourth root is: '), disp(s(4));
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));Po uruchomieniu pliku zwraca następujący wynik -
The first root is:
6.630396332390718431485053218985
The second root is:
1.0597804633025896291682772499885
The third root is:
- 0.34508839784665403032666523448675 - 1.0778362954630176596831109269793*i
The fourth root is:
- 0.34508839784665403032666523448675 + 1.0778362954630176596831109269793*i
Numeric value of first root
6.6304
Numeric value of second root
1.0598
Numeric value of third root
-0.3451 - 1.0778i
Numeric value of fourth root
-0.3451 + 1.0778iZwróć uwagę, że ostatnie dwa pierwiastki to liczby zespolone.
Rozwiązywanie równań wyższego rzędu w oktawach
Poniższy przykład rozwiązuje równanie czwartego rzędu x 4 - 7x 3 + 3x 2 - 5x + 9 = 0.
Utwórz plik skryptu i wpisz następujący kod -
v = [1, -7, 3, -5, 9];
s = roots(v);
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));Po uruchomieniu pliku zwraca następujący wynik -
Numeric value of first root
6.6304
Numeric value of second root
-0.34509 + 1.07784i
Numeric value of third root
-0.34509 - 1.07784i
Numeric value of fourth root
1.0598Rozwiązywanie układu równań w programie MATLAB
Plik solveFunkcja może również służyć do generowania rozwiązań układów równań zawierających więcej niż jedną zmienną. Podajmy prosty przykład, aby zademonstrować to zastosowanie.
Rozwiążmy równania -
5x + 9y = 5
3x - 6 lat = 4
Utwórz plik skryptu i wpisz następujący kod -
s = solve('5*x + 9*y = 5','3*x - 6*y = 4');
s.x
s.yPo uruchomieniu pliku wyświetla następujący wynik -
ans =
22/19
ans =
-5/57W ten sam sposób możesz rozwiązać większe układy liniowe. Rozważmy następujący zestaw równań -
x + 3y -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8
Rozwiązywanie układu równań w oktawie
Mamy trochę inne podejście do rozwiązania układu „n” równań liniowych w „n” niewiadomych. Podajmy prosty przykład, aby zademonstrować to zastosowanie.
Rozwiążmy równania -
5x + 9y = 5
3x - 6 lat = 4
Taki układ równań liniowych można zapisać jako pojedyncze równanie macierzowe Ax = b, gdzie A to macierz współczynników, b to wektor kolumnowy zawierający prawą stronę równań liniowych, a x to wektor kolumnowy reprezentujący rozwiązanie jako pokazane w poniższym programie -
Utwórz plik skryptu i wpisz następujący kod -
A = [5, 9; 3, -6];
b = [5;4];
A \ bPo uruchomieniu pliku wyświetla następujący wynik -
ans =
1.157895
-0.087719W ten sam sposób możesz rozwiązać większe układy liniowe, jak podano poniżej -
x + 3y -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8
Rozwijanie i zbieranie równań w MATLAB
Plik expand i collectfunkcja odpowiednio rozwija i zbiera równanie. Poniższy przykład ilustruje koncepcje -
Kiedy pracujesz z wieloma funkcjami symbolicznymi, powinieneś zadeklarować, że twoje zmienne są symboliczne.
Utwórz plik skryptu i wpisz następujący kod -
syms x %symbolic variable x
syms y %symbolic variable x
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(sin(2*x))
expand(cos(x+y))
% collecting equations
collect(x^3 *(x-7))
collect(x^4*(x-3)*(x-5))Po uruchomieniu pliku wyświetla następujący wynik -
ans =
x^2 + 4*x - 45
ans =
x^4 + x^3 - 43*x^2 + 23*x + 210
ans =
2*cos(x)*sin(x)
ans =
cos(x)*cos(y) - sin(x)*sin(y)
ans =
x^4 - 7*x^3
ans =
x^6 - 8*x^5 + 15*x^4Rozszerzanie i zbieranie równań w oktawie
Musisz mieć symbolic pakiet, który zapewnia expand i collectfunkcji, aby odpowiednio rozwinąć i zebrać równanie. Poniższy przykład ilustruje koncepcje -
Podczas pracy z wieloma funkcjami symbolicznymi należy zadeklarować, że zmienne są symboliczne, ale Octave ma inne podejście do definiowania zmiennych symbolicznych. Zwróć uwagę na użycieSin i Cos, które są również zdefiniowane w pakiecie symbolicznym.
Utwórz plik skryptu i wpisz następujący kod -
% first of all load the package, make sure its installed.
pkg load symbolic
% make symbols module available
symbols
% define symbolic variables
x = sym ('x');
y = sym ('y');
z = sym ('z');
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(Sin(2*x))
expand(Cos(x+y))
% collecting equations
collect(x^3 *(x-7), z)
collect(x^4*(x-3)*(x-5), z)Po uruchomieniu pliku wyświetla następujący wynik -
ans =
-45.0+x^2+(4.0)*x
ans =
210.0+x^4-(43.0)*x^2+x^3+(23.0)*x
ans =
sin((2.0)*x)
ans =
cos(y+x)
ans =
x^(3.0)*(-7.0+x)
ans =
(-3.0+x)*x^(4.0)*(-5.0+x)Faktoryzacja i upraszczanie wyrażeń algebraicznych
Plik factor funkcja rozkłada na czynniki wyrażenie, a simplifyfunkcja upraszcza wyrażenie. Poniższy przykład ilustruje koncepcję -
Przykład
Utwórz plik skryptu i wpisz następujący kod -
syms x
syms y
factor(x^3 - y^3)
factor([x^2-y^2,x^3+y^3])
simplify((x^4-16)/(x^2-4))Po uruchomieniu pliku wyświetla następujący wynik -
ans =
(x - y)*(x^2 + x*y + y^2)
ans =
[ (x - y)*(x + y), (x + y)*(x^2 - x*y + y^2)]
ans =
x^2 + 4MATLAB zapewnia różne sposoby rozwiązywania problemów rachunku różniczkowego i całkowego, rozwiązywania równań różniczkowych dowolnego stopnia oraz obliczania granic. Co najlepsze, możesz łatwo wykreślić wykresy złożonych funkcji i sprawdzić maksima, minima i inne punkty stacjonarne na wykresie, rozwiązując pierwotną funkcję, a także jej pochodną.
W tym rozdziale zajmiemy się zagadnieniami rachunku różniczkowego. W tym rozdziale omówimy koncepcje przed rachunkiem, czyli obliczanie granic funkcji i weryfikację własności granic.
W następnym rozdziale Różniczkowanie obliczymy pochodną wyrażenia i znajdziemy lokalne maksima i minima na wykresie. Omówimy również rozwiązywanie równań różniczkowych.
Na koniec w rozdziale Integracja omówimy rachunek całkowy.
Obliczanie limitów
MATLAB zapewnia limitfunkcja obliczania limitów. W swojej najbardziej podstawowej formielimit funkcja przyjmuje wyrażenie jako argument i znajduje granicę wyrażenia, gdy zmienna niezależna osiąga zero.
Na przykład obliczmy granicę funkcji f (x) = (x 3 + 5) / (x 4 + 7), ponieważ x dąży do zera.
syms x
limit((x^3 + 5)/(x^4 + 7))MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
5/7Funkcja graniczna należy do dziedziny obliczeń symbolicznych; musisz użyćsymsfunkcja, aby poinformować MATLAB, których zmiennych symbolicznych używasz. Możesz również obliczyć limit funkcji, ponieważ zmienna zmierza do pewnej liczby innej niż zero. Aby obliczyć lim x-> a (f (x)), używamy polecenia limit z argumentami. Pierwsza to wyrażenie, a druga to liczba, do której zbliża się x , tutaj jest to a .
Na przykład obliczmy granicę funkcji f (x) = (x-3) / (x-1), ponieważ x dąży do 1.
limit((x - 3)/(x-1),1)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
NaNWeźmy inny przykład,
limit(x^2 + 5, 3)MATLAB wykona powyższą instrukcję i zwróci następujący wynik -
ans =
14Obliczanie granic za pomocą oktawy
Poniżej znajduje się wersja Octave powyższego przykładu wykorzystująca symbolic pakiet, spróbuj wykonać i porównać wynik -
pkg load symbolic
symbols
x = sym("x");
subs((x^3+5)/(x^4+7),x,0)Octave wykona powyższą instrukcję i zwróci następujący wynik -
ans =
0.7142857142857142857Weryfikacja podstawowych właściwości granic
Algebraiczne twierdzenie o granicach dostarcza podstawowych własności granic. Są to następujące -
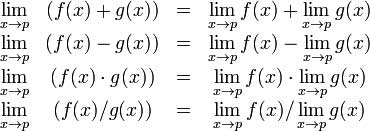
Rozważmy dwie funkcje -
- f (x) = (3x + 5) / (x - 3)
- g (x) = x 2 + 1.
Obliczmy granice funkcji, jak x dąży do 5, obu funkcji i zweryfikujmy podstawowe właściwości granic przy użyciu tych dwóch funkcji i MATLABA.
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)Po uruchomieniu pliku wyświetla się -
l1 =
17
l2 =
17
lAdd =
34
lSub =
0
lMult =
289
lDiv =
1Weryfikacja podstawowych właściwości granic za pomocą oktawy
Poniżej znajduje się wersja Octave powyższego przykładu wykorzystująca symbolic pakiet, spróbuj wykonać i porównać wynik -
pkg load symbolic
symbols
x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)Octave wykona powyższą instrukcję i zwróci następujący wynik -
l1 =
17.0
l2 =
17.0
lAdd =
34.0
lSub =
0.0
lMult =
289.0
lDiv =
1.0Limity lewostronne i prawostronne
Gdy funkcja ma nieciągłość dla jakiejś określonej wartości zmiennej, granica nie istnieje w tym punkcie. Innymi słowy, granice funkcji f (x) mają nieciągłość przy x = a, gdy wartość granicy, gdy x zbliża się do x z lewej strony, nie jest równa wartości granicy, gdy x zbliża się z prawej strony.
Prowadzi to do koncepcji granic leworęcznych i praworęcznych. Granica leworęczna jest definiowana jako granica jako x -> a, od lewej, tj. X zbliża się do a, dla wartości x <a. Granica prawostronna jest definiowana jako granica jako x -> a, od prawej strony, tj. X zbliża się do a, dla wartości x> a. Kiedy limit dla leworęcznych i praworęcznych nie są równe, limit nie istnieje.
Rozważmy funkcję -
f(x) = (x - 3)/|x - 3|
Pokażemy, że lim x-> 3 f (x) nie istnieje. MATLAB pomaga nam ustalić ten fakt na dwa sposoby -
- Poprzez wykreślenie wykresu funkcji i pokazanie nieciągłości.
- Obliczając granice i pokazując, że oba są różne.
Limity dla leworęcznych i praworęcznych są obliczane przez przekazanie ciągów znaków „lewo” i „prawo” do polecenia limitu jako ostatniego argumentu.
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')Po uruchomieniu pliku MATLAB rysuje następujący wykres
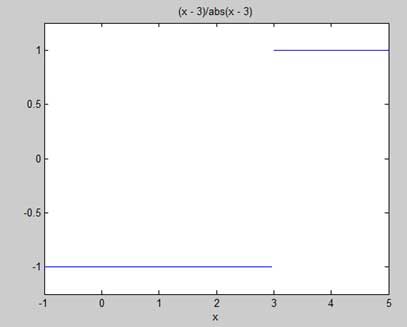
Po wyświetleniu tego wyjścia -
l =
-1
r =
1MATLAB zapewnia diffpolecenie do obliczania pochodnych symbolicznych. W najprostszej formie jako argument przekazujesz funkcję, którą chcesz odróżnić, do polecenia diff.
Na przykład obliczmy pochodną funkcji f (t) = 3t 2 + 2t -2
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
syms t
f = 3*t^2 + 2*t^(-2);
diff(f)Kiedy powyższy kod jest kompilowany i wykonywany, daje następujący wynik -
ans =
6*t - 4/t^3Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)Octave wykonuje kod i zwraca następujący wynik -
ans =
-(4.0)*t^(-3.0)+(6.0)*tWeryfikacja elementarnych reguł różnicowania
Przedstawmy pokrótce różne równania lub reguły różniczkowania funkcji i zweryfikujmy te zasady. W tym celu zapiszemy f '(x) dla pochodnej pierwszego rzędu, a f "(x) dla pochodnej drugiego rzędu.
Oto zasady różnicowania -
Zasada nr 1
Dla dowolnych funkcji f i g oraz dowolnych liczb rzeczywistych a i b są pochodną funkcji -
h(x) = af(x) + bg(x) w odniesieniu do x jest dane przez -
h'(x) = af'(x) + bg'(x)
Zasada 2
Plik sum i subtraction reguły mówią, że jeśli f i g są dwiema funkcjami, to odpowiednio f 'i g' są ich pochodnymi, to
(f + g)' = f' + g'
(f - g)' = f' - g'
Zasada 3
Plik product reguła mówi, że jeśli f i g są dwiema funkcjami, to odpowiednio f 'i g' są ich pochodnymi, to
(f.g)' = f'.g + g'.f
Zasada 4
Plik quotient reguła mówi, że jeśli f i g są dwiema funkcjami, to odpowiednio f 'i g' są ich pochodnymi, to
(f/g)' = (f'.g - g'.f)/g2
Zasada 5
Plik polynomial lub elementarna reguła władzy mówi, że jeśli y = f(x) = xn, następnie f' = n. x(n-1)
Bezpośrednim skutkiem tej reguły jest to, że pochodna dowolnej stałej wynosi zero, tj. Jeśli y = k, więc jakakolwiek stała
f' = 0
Zasada 6
Plik chain reguła stwierdza, że pochodna funkcji funkcji h(x) = f(g(x)) w odniesieniu do x jest,
h'(x)= f'(g(x)).g'(x)
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
syms x
syms t
f = (x + 2)*(x^2 + 3)
der1 = diff(f)
f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)
f = (x^2 + 1)^17
der5 = diff(f)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)Po uruchomieniu pliku MATLAB wyświetla następujący wynik -
f =
(x^2 + 3)*(x + 2)
der1 =
2*x*(x + 2) + x^2 + 3
f =
(t^(1/2) + t^3)*(t^2 + 3)
der2 =
(t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
f =
(x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 =
(2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
f =
(2*x^2 + 3*x)/(x^3 + 1)
der4 =
(4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
f =
(x^2 + 1)^17
der5 =
34*x*(x^2 + 1)^16
f =
1/(t^3 + 3*t^2 + 5*t - 9)^6
der6 =
-(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)Octave wykonuje kod i zwraca następujący wynik -
f =
(2.0+x)*(3.0+x^(2.0))
der1 =
3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =
(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =
(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =
(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =
(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =
(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =
(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =
(1.0+x^(2.0))^(17.0)
der5 =
(34.0)*(1.0+x^(2.0))^(16.0)*x
f =
(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =
-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)Pochodne funkcji wykładniczej, logarytmicznej i trygonometrycznej
Poniższa tabela przedstawia pochodne powszechnie używanych funkcji wykładniczych, logarytmicznych i trygonometrycznych -
| Funkcjonować | Pochodna |
|---|---|
| ca.x | c a.x .ln ca (ln to logarytm naturalny) |
| ex | e x |
| ln x | 1 / x |
| lncx | 1 / x.ln c |
| xx | x x . (1 + ln x) |
| sin(x) | cos (x) |
| cos(x) | -sin (x) |
| tan(x) | sec 2 (x) lub 1 / cos 2 (x) lub 1 + tan 2 (x) |
| cot(x) | -csc 2 (x) lub -1 / sin 2 (x) lub - (1 + cot 2 (x)) |
| sec(x) | sec (x). tan (x) |
| csc(x) | -csc (x) .cot (x) |
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
syms x
y = exp(x)
diff(y)
y = x^9
diff(y)
y = sin(x)
diff(y)
y = tan(x)
diff(y)
y = cos(x)
diff(y)
y = log(x)
diff(y)
y = log10(x)
diff(y)
y = sin(x)^2
diff(y)
y = cos(3*x^2 + 2*x + 1)
diff(y)
y = exp(x)/sin(x)
diff(y)Po uruchomieniu pliku MATLAB wyświetla następujący wynik -
y =
exp(x)
ans =
exp(x)
y =
x^9
ans =
9*x^8
y =
sin(x)
ans =
cos(x)
y =
tan(x)
ans =
tan(x)^2 + 1
y =
cos(x)
ans =
-sin(x)
y =
log(x)
ans =
1/x
y =
log(x)/log(10)
ans =
1/(x*log(10))
y =
sin(x)^2
ans =
2*cos(x)*sin(x)
y =
cos(3*x^2 + 2*x + 1)
ans =
-sin(3*x^2 + 2*x + 1)*(6*x + 2)
y =
exp(x)/sin(x)
ans =
exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)Octave wykonuje kod i zwraca następujący wynik -
y =
exp(x)
ans =
exp(x)
y =
x^(9.0)
ans =
(9.0)*x^(8.0)
y =
sin(x)
ans =
cos(x)
y =
tan(x)
ans =
1+tan(x)^2
y =
cos(x)
ans =
-sin(x)
y =
log(x)
ans =
x^(-1)
y =
sin(x)^(2.0)
ans =
(2.0)*sin(x)*cos(x)
y =
cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =
-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =
sin(x)^(-1)*exp(x)
ans =
sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)Obliczanie pochodnych wyższego rzędu
Aby obliczyć wyższe pochodne funkcji f, używamy składni diff(f,n).
Obliczmy drugą pochodną funkcji y = f (x) = x. E -3x
f = x*exp(-3*x);
diff(f, 2)MATLAB wykonuje kod i zwraca następujący wynik -
ans =
9*x*exp(-3*x) - 6*exp(-3*x)Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)Octave wykonuje kod i zwraca następujący wynik -
ans =
(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)Przykład
W tym przykładzie rozwiążmy problem. Biorąc pod uwagę, że funkcjay = f(x) = 3 sin(x) + 7 cos(5x). Będziemy musieli dowiedzieć się, czy równanief" + f = -5cos(2x) trzyma się prawdy.
Utwórz plik skryptu i wpisz w nim następujący kod -
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);Po uruchomieniu pliku wyświetla następujący wynik -
No, the equation does not hold true
Value of LHS is:
-168*cos(5*x)Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);Octave wykonuje kod i zwraca następujący wynik -
No, the equation does not hold true
Value of LHS is:
-(168.0)*cos((5.0)*x)Znajdowanie maksimów i minimów krzywej
Jeśli szukamy lokalnych maksimów i minimów dla wykresu, w zasadzie szukamy najwyższych lub najniższych punktów na wykresie funkcji w określonej miejscowości lub określonego zakresu wartości zmiennej symbolicznej.
Dla funkcji y = f (x) nazywane są punkty na wykresie, w których wykres ma nachylenie zerowe stationary points. Innymi słowy, punkty stacjonarne to punkty, w których f '(x) = 0.
Aby znaleźć punkty stacjonarne funkcji, którą rozróżniamy, musimy ustawić pochodną równą zero i rozwiązać równanie.
Przykład
Znajdźmy punkty stacjonarne funkcji f (x) = 2x 3 + 3x 2 - 12x + 17
Wykonaj następujące kroki -
First let us enter the function and plot its graph.
syms x
y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function
ezplot(y)MATLAB wykonuje kod i zwraca następujący wykres -
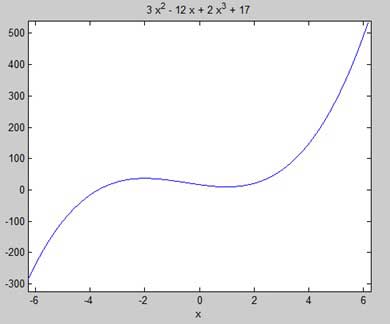
Oto odpowiednik oktawy dla powyższego przykładu -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.epsOur aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.
syms x
y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function
ezplot(y, [-2, 2])MATLAB wykonuje kod i zwraca następujący wykres -
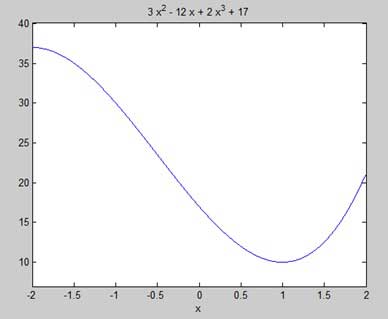
Oto odpowiednik oktawy dla powyższego przykładu -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.epsNext, let us compute the derivative.
g = diff(y)MATLAB wykonuje kod i zwraca następujący wynik -
g =
6*x^2 + 6*x - 12Oto odpowiednik oktawy powyższego obliczenia -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)Octave wykonuje kod i zwraca następujący wynik -
g =
-12.0+(6.0)*x+(6.0)*x^(2.0)Let us solve the derivative function, g, to get the values where it becomes zero.
s = solve(g)MATLAB wykonuje kod i zwraca następujący wynik -
s =
1
-2Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])Octave wykonuje kod i zwraca następujący wynik -
g =
-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =
-2
1This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. Możemy zastąpić wartość w funkcji symbolicznej za pomocą subs Komenda.
subs(y, 1), subs(y, -2)MATLAB wykonuje kod i zwraca następujący wynik -
ans =
10
ans =
37Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)ans =
10.0
ans =
37.0-4.6734207789940138748E-18*IDlatego wartości minimalne i maksymalne funkcji f (x) = 2x 3 + 3x 2 - 12x + 17, w przedziale [-2,2] wynoszą 10 i 37.
Rozwiązywanie równań różniczkowych
MATLAB zapewnia dsolve polecenie do symbolicznego rozwiązywania równań różniczkowych.
Najbardziej podstawowa forma dsolve polecenie znalezienia rozwiązania pojedynczego równania to
dsolve('eqn')gdzie eqn to ciąg tekstowy używany do wprowadzania równania.
Zwraca symboliczne rozwiązanie z zestawem dowolnych stałych, które MATLAB oznacza C1, C2 i tak dalej.
Możesz również określić warunki początkowe i brzegowe dla problemu, jako listę rozdzielaną przecinkami po równaniu jako -
dsolve('eqn','cond1', 'cond2',…)W celu użycia polecenia dsolve, derivatives are indicated with a D. Na przykład równanie takie jak f '(t) = -2 * f + koszt (t) jest wprowadzane jako -
'Df = -2*f + cos(t)'
Wyższe pochodne są wskazywane za pomocą następującego po D kolejności pochodnej.
Na przykład równanie f "(x) + 2f '(x) = 5sin3x należy wpisać jako -
'D2y + 2Dy = 5*sin(3*x)'
Weźmy prosty przykład równania różniczkowego pierwszego rzędu: y '= 5y.
s = dsolve('Dy = 5*y')MATLAB wykonuje kod i zwraca następujący wynik -
s =
C2*exp(5*t)Weźmy inny przykład równania różniczkowego drugiego rzędu jako: y "- y = 0, y (0) = -1, y '(0) = 2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')MATLAB wykonuje kod i zwraca następujący wynik -
ans =
exp(t)/2 - (3*exp(-t))/2Integracja dotyczy dwóch zasadniczo różnych typów problemów.
W pierwszym typie dana jest pochodna funkcji i chcemy znaleźć funkcję. Dlatego w zasadzie odwracamy proces różnicowania. Ten odwrotny proces jest znany jako anty-różnicowanie lub znajdowanie funkcji pierwotnej lub znajdowanieindefinite integral.
Drugi rodzaj problemów polega na dodaniu bardzo dużej liczby bardzo małych wielkości, a następnie przyjęciu granicy, gdy wielkość wielkości zbliża się do zera, podczas gdy liczba składników ma tendencję do nieskończoności. Ten proces prowadzi do zdefiniowania plikudefinite integral.
Całki oznaczone są używane do wyznaczania pola powierzchni, objętości, środka ciężkości, momentu bezwładności, pracy wykonanej przez siłę oraz w wielu innych zastosowaniach.
Znajdowanie całki nieokreślonej za pomocą MATLAB
Z definicji, jeśli pochodną funkcji f (x) jest f '(x), to mówimy, że całka nieoznaczona f' (x) względem x jest f (x). Na przykład, ponieważ pochodna (względem x) x 2 wynosi 2x, możemy powiedzieć, że całka nieoznaczona z 2x wynosi x 2 .
W symbolach -
f'(x2) = 2x, w związku z tym,
∫ 2xdx = x2.
Całka nieoznaczona nie jest unikatowa, ponieważ pochodna x 2 + c dla dowolnej wartości stałej c będzie również 2x.
Jest to wyrażone za pomocą symboli jako -
∫ 2xdx = x2 + c.
Gdzie c nazywa się „dowolną stałą”.
MATLAB zapewnia intpolecenie do obliczania całki wyrażenia. Aby wyprowadzić wyrażenie na całkę nieoznaczoną funkcji, piszemy -
int(f);Na przykład z naszego poprzedniego przykładu -
syms x
int(2*x)MATLAB wykonuje powyższą instrukcję i zwraca następujący wynik -
ans =
x^2Przykład 1
W tym przykładzie znajdźmy całkę z niektórych powszechnie używanych wyrażeń. Utwórz plik skryptu i wpisz w nim następujący kod -
syms x n
int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)Po uruchomieniu pliku wyświetla następujący wynik -
ans =
piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
-cos(n*t)/n
ans =
(a*sin(pi*t))/pi
ans =
a^x/log(a)Przykład 2
Utwórz plik skryptu i wpisz w nim następujący kod -
syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))Zwróć uwagę, że pretty funkcja zwraca wyrażenie w bardziej czytelnym formacie.
Po uruchomieniu pliku wyświetla następujący wynik -
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2Znajdowanie całki oznaczonej za pomocą MATLAB
Z definicji całka oznaczona jest w zasadzie granicą sumy. Używamy całek oznaczonych, aby znaleźć obszary, takie jak pole między krzywą a osią x oraz pole między dwiema krzywymi. Całki oznaczone można również stosować w innych sytuacjach, w których wymaganą ilość można wyrazić jako granicę sumy.
Plik int funkcja może być używana do całkowania określonego przez przekazanie granic, powyżej których chcesz obliczyć całkę.
Liczyć
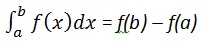
piszemy,
int(x, a, b)Na przykład, aby obliczyć wartość

int(x, 4, 9)MATLAB wykonuje powyższą instrukcję i zwraca następujący wynik -
ans =
65/2Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));Octave wykonuje kod i zwraca następujący wynik -
Area:
32.500Alternatywne rozwiązanie można podać za pomocą funkcji quad () udostępnianej przez Octave w następujący sposób -
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));Octave wykonuje kod i zwraca następujący wynik -
Area:
32.500Przykład 1
Obliczmy obszar zawarty między osią x, krzywą y = x 3 −2x + 5 oraz rzędnymi x = 1 i x = 2.
Wymagany obszar określa -
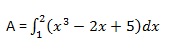
Utwórz plik skryptu i wpisz następujący kod -
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));Po uruchomieniu pliku wyświetla następujący wynik -
a =
23/4
Area:
5.7500Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));Octave wykonuje kod i zwraca następujący wynik -
Area:
5.7500Alternatywne rozwiązanie można podać za pomocą funkcji quad () udostępnianej przez Octave w następujący sposób -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));Octave wykonuje kod i zwraca następujący wynik -
Area:
5.7500Przykład 2
Znajdź pole pod krzywą: f (x) = x 2 cos (x) dla −4 ≤ x ≤ 9.
Utwórz plik skryptu i napisz następujący kod -
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));Po uruchomieniu pliku MATLAB wykreśla wykres -
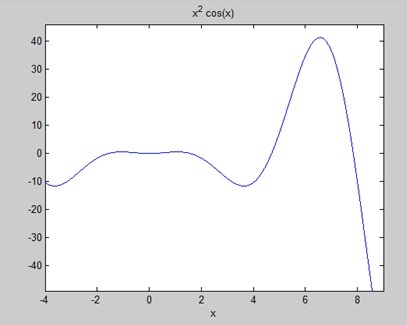
Dane wyjściowe podano poniżej -
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));MATLAB reprezentuje wielomiany jako wektory wierszowe zawierające współczynniki uporządkowane według malejących potęg. Na przykład równanie P (x) = x 4 + 7x 3 - 5x + 9 można przedstawić jako -
p = [1 7 0–5 9];
Ocenianie wielomianów
Plik polyvalfunkcja służy do obliczania wielomianu o określonej wartości. Na przykład, aby ocenić nasz poprzedni wielomianp, przy x = 4, wpisz -
p = [1 7 0 -5 9];
polyval(p,4)MATLAB wykonuje powyższe instrukcje i zwraca następujący wynik -
ans = 693MATLAB zapewnia również polyvalmfunkcja do obliczania wielomianu macierzy. Wielomian macierzowy topolynomial z macierzami jako zmiennymi.
Na przykład, stwórzmy kwadratową macierz X i obliczmy wielomian p przy X -
p = [1 7 0 -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)MATLAB wykonuje powyższe instrukcje i zwraca następujący wynik -
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269Znajdowanie korzeni wielomianów
Plik rootsfunkcja oblicza pierwiastki wielomianu. Na przykład, aby obliczyć pierwiastki naszego wielomianu p, wpisz -
p = [1 7 0 -5 9];
r = roots(p)MATLAB wykonuje powyższe instrukcje i zwraca następujący wynik -
r =
-6.8661 + 0.0000i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095iFunkcja polyjest odwrotnością funkcji pierwiastków i wraca do współczynników wielomianu. Na przykład -
p2 = poly(r)MATLAB wykonuje powyższe instrukcje i zwraca następujący wynik -
p2 =
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000iDopasowanie krzywej wielomianowej
Plik polyfitfunkcja znajduje współczynniki wielomianu, który pasuje do zbioru danych w sensie najmniejszych kwadratów. Jeśli x i y są dwoma wektorami zawierającymi dane xiy, które mają zostać dopasowane do wielomianu n-stopniowego, to otrzymujemy wielomian pasujący do danych, pisząc -
p = polyfit(x,y,n)Przykład
Utwórz plik skryptu i wpisz następujący kod -
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid onPo uruchomieniu pliku MATLAB wyświetla następujący wynik -
p =
4.1056 -47.9607 222.2598 -362.7453 191.1250I wykreśla następujący wykres -
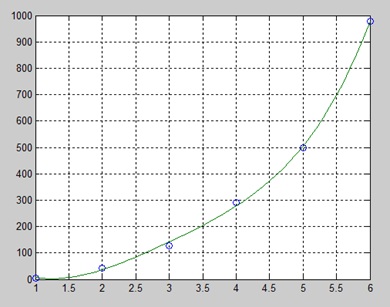
MATLAB udostępnia polecenia do pracy z transformacjami, takimi jak transformaty Laplace'a i Fouriera. Transformacje są wykorzystywane w nauce i inżynierii jako narzędzie upraszczające analizę i spoglądanie na dane z innej perspektywy.
Na przykład transformata Fouriera pozwala nam przekształcić sygnał przedstawiony jako funkcja czasu na funkcję częstotliwości. Przekształcenie Laplace'a pozwala nam przekształcić równanie różniczkowe w równanie algebraiczne.
MATLAB zapewnia laplace, fourier i fft polecenia do pracy z transformatami Laplace'a, Fouriera i Fast Fouriera.
Transformata Laplace'a
Transformata Laplace'a funkcji czasu f (t) jest dana następującą całką -
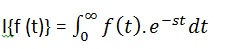
Transformata Laplace'a jest również oznaczana jako transformacja f (t) do F (s). Możesz zobaczyć, jak ten proces transformacji lub integracji przekształca f (t), funkcję zmiennej symbolicznej t, na inną funkcję F (s) z inną zmienną s.
Transformata Laplace'a przekształca równania różniczkowe w algebraiczne. Aby obliczyć transformację Laplace'a funkcji f (t), napisz -
laplace(f(t))Przykład
W tym przykładzie obliczymy transformację Laplace'a niektórych powszechnie używanych funkcji.
Utwórz plik skryptu i wpisz następujący kod -
syms s t a b w
laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))Po uruchomieniu pliku wyświetla następujący wynik -
ans =
1/s^2
ans =
2/s^3
ans =
362880/s^10
ans =
1/(b + s)
ans =
w/(s^2 + w^2)
ans =
s/(s^2 + w^2)Odwrotna transformata Laplace'a
MATLAB pozwala nam obliczyć odwrotną transformatę Laplace'a za pomocą polecenia ilaplace.
Na przykład,
ilaplace(1/s^3)MATLAB wykona powyższą instrukcję i wyświetli wynik -
ans =
t^2/2Przykład
Utwórz plik skryptu i wpisz następujący kod -
syms s t a b w
ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))Po uruchomieniu pliku wyświetla następujący wynik -
ans =
t^6/720
ans =
2*exp(-t*w)
ans =
cos(2*t)
ans =
ilaplace(exp(-b*t), t, x)
ans =
sin(t*w)
ans =
cos(t*w)Transformacje Fouriera
Transformaty Fouriera zwykle przekształcają matematyczną funkcję czasu, f (t), w nową funkcję, czasami oznaczaną przez lub F, której argumentem jest częstotliwość z jednostkami cykli / s (herc) lub radianami na sekundę. Nowa funkcja jest wtedy znana jako transformata Fouriera i / lub widmo częstotliwości funkcji f.
Przykład
Utwórz plik skryptu i wpisz w nim następujący kod -
syms x
f = exp(-2*x^2); %our function
ezplot(f,[-2,2]) % plot of our function
FT = fourier(f) % Fourier transformPo uruchomieniu pliku MATLAB wykreśla następujący wykres -
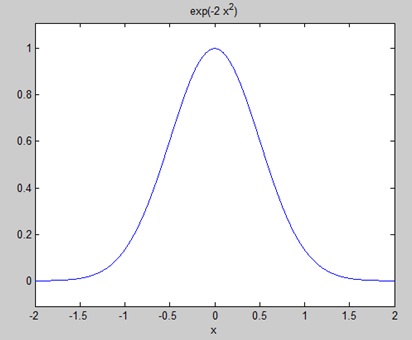
Wyświetlany jest następujący wynik -
FT =
(2^(1/2)*pi^(1/2)*exp(-w^2/8))/2Wykreślanie transformaty Fouriera jako -
ezplot(FT)Daje następujący wykres -

Odwrotne transformaty Fouriera
MATLAB zapewnia ifourierpolecenie do obliczenia odwrotnej transformaty Fouriera funkcji. Na przykład,
f = ifourier(-2*exp(-abs(w)))MATLAB wykona powyższą instrukcję i wyświetli wynik -
f =
-2/(pi*(x^2 + 1))GNU Octave jest językiem programowania wysokiego poziomu, takim jak MATLAB i jest w większości kompatybilny z MATLAB. Jest również używany do obliczeń numerycznych.
Octave ma następujące wspólne cechy z MATLAB -
- macierze to podstawowy typ danych
- ma wbudowaną obsługę liczb zespolonych
- ma wbudowane funkcje matematyczne i biblioteki
- obsługuje funkcje zdefiniowane przez użytkownika
GNU Octave jest również oprogramowaniem, które można dowolnie rozpowszechniać. Możesz go rozpowszechniać i / lub modyfikować zgodnie z warunkami Powszechnej Licencji Publicznej GNU (GPL) opublikowanej przez Free Software Foundation.
MATLAB vs Octave
Większość programów MATLAB działa w Octave, ale niektóre programy Octave mogą nie działać w MATLAB-ie, ponieważ Octave pozwala na składnię, której MATLAB nie obsługuje.
Na przykład MATLAB obsługuje tylko pojedyncze cudzysłowy, ale Octave obsługuje zarówno pojedyncze, jak i podwójne cudzysłowy do definiowania ciągów. Jeśli szukasz samouczka na temat Octave, przejrzyj ten samouczek od początku, który obejmuje zarówno MATLAB, jak i Octave.
Zgodne przykłady
Prawie wszystkie przykłady omówione w tym samouczku są kompatybilne zarówno z MATLAB, jak iz Octave. Wypróbujmy następujący przykład w MATLAB i Octave, który daje ten sam wynik bez żadnych zmian składni -
Ten przykład tworzy trójwymiarową mapę powierzchni dla funkcji g = xe - (x 2 + y 2 ) . Utwórz plik skryptu i wpisz następujący kod -
[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.epsPo uruchomieniu pliku MATLAB wyświetla następującą mapę 3-W -

Niezgodne przykłady
Chociaż cała podstawowa funkcjonalność MATLAB-a jest dostępna w Octave, istnieją pewne funkcje, na przykład rachunek różniczkowy i całkowy, który nie pasuje dokładnie w obu językach. W tym samouczku próbowano podać przykłady obu typów, w których różniły się one składnią.
Rozważmy następujący przykład, w którym MATLAB i Octave używają różnych funkcji, aby uzyskać pole krzywej: f (x) = x 2 cos (x) dla −4 ≤ x ≤ 9. Poniżej znajduje się wersja kodu MATLAB -
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));Po uruchomieniu pliku MATLAB wykreśla wykres -

Wyświetlany jest następujący wynik
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326Ale aby podać obszar tej samej krzywej w oktawie, będziesz musiał wykorzystać symbolic pakiet w następujący sposób -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));Simulink to środowisko projektowania oparte na symulacji i modelach dla systemów dynamicznych i wbudowanych, zintegrowane z MATLAB. Simulink, również opracowany przez MathWorks, jest graficznym językiem programowania przepływu danych do modelowania, symulacji i analizy wielodomenowych systemów dynamicznych. Jest to w zasadzie graficzne narzędzie do tworzenia diagramów blokowych z konfigurowalnym zestawem bibliotek bloków.
Umożliwia włączenie algorytmów MATLAB do modeli, a także eksport wyników symulacji do MATLAB w celu dalszej analizy.
Simulink obsługuje -
- projekt na poziomie systemu
- simulation
- automatyczne generowanie kodu
- testowanie i weryfikacja systemów wbudowanych
Istnieje kilka innych produktów dodatkowych dostarczanych przez MathWorks oraz sprzęt i oprogramowanie innych firm, które są dostępne do użytku z Simulink.
Poniższa lista zawiera krótki opis niektórych z nich -
Stateflow umożliwia tworzenie maszyn stanu i schematów blokowych.
Simulink Coder umożliwia automatyczne generowanie kodu źródłowego w języku C do automatycznego wdrażania systemów w czasie rzeczywistym.
xPC Target razem z x86-based real-time systems zapewniają środowisko do symulacji i testowania modeli Simulink i Stateflow w czasie rzeczywistym w systemie fizycznym.
Embedded Coder obsługuje określone osadzone cele.
HDL Coder pozwala na automatyczne generowanie syntezowalnych VHDL i Verilog.
SimEvents udostępnia bibliotekę graficznych bloków konstrukcyjnych do modelowania systemów kolejkowania.
Simulink umożliwia systematyczną weryfikację i walidację modeli poprzez sprawdzanie stylu modelowania, śledzenie wymagań i analizę pokrycia modelu.
Simulink Design Verifier umożliwia identyfikację błędów projektowych i generowanie scenariuszy testowych do sprawdzania modeli.
Korzystanie z Simulink
Aby otworzyć Simulink, wpisz obszar roboczy MATLAB -
simulinkSimulink otwiera Library Browser. Przeglądarka biblioteki służy do tworzenia modeli symulacyjnych.

W lewym panelu okna znajduje się kilka bibliotek podzielonych na kategorie na podstawie różnych systemów, kliknięcie każdego z nich spowoduje wyświetlenie bloków projektowych w prawym panelu.
Budowanie modeli
Aby utworzyć nowy model, kliknij Newna pasku narzędzi przeglądarki biblioteki. Otworzy się nowe okno modelu bez tytułu.
Model Simulink to schemat blokowy.
Elementy modelu dodaje się, wybierając odpowiednie elementy z przeglądarki biblioteki i przeciągając je do okna modelu.
Alternatywnie możesz skopiować elementy modelu i wkleić je do okna modelu.
Przykłady
Przeciągnij i upuść elementy z biblioteki Simulink, aby stworzyć swój projekt.
Na potrzeby tego przykładu do symulacji zostaną wykorzystane dwa bloki - A Source (sygnał) i a Sink(zakres). Generator sygnału (źródło) generuje sygnał analogowy, który jest następnie wizualizowany graficznie przez oscyloskop (ujście).
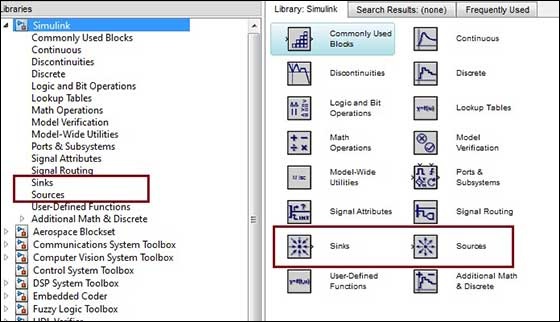
Rozpocznij od przeciągnięcia wymaganych bloków z biblioteki do okna projektu. Następnie połącz bloki ze sobą, co można zrobić, przeciągając złącza z punktów połączeń w jednym bloku do punktów w drugim.
Przeciągnijmy do modelu blok „Sine Wave”.
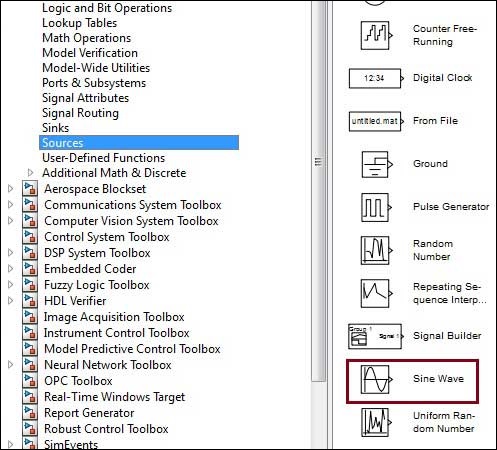
Wybierz „Zlewy” z biblioteki i przeciągnij blok „Zakres” do modelu.
Przeciągnij linię sygnału z wyjścia bloku sinusoidalnego do wejścia bloku oscyloskopu.
Uruchom symulację naciskając 'Runprzycisk ', zachowując wszystkie parametry domyślne (możesz je zmienić w menu Symulacja)
Z lunety powinieneś otrzymać poniższy wykres.