Systemy radarowe - niwelatory linii opóźniającej
W tym rozdziale dowiemy się o eliminatorach linii opóźniającej w systemach radarowych. Jak sama nazwa wskazuje, linia opóźniająca wprowadza pewne opóźnienie. Tak więc linia opóźniająca jest używana głównie w kasowaniu linii opóźniającej w celu wprowadzeniadelay czasu powtarzania impulsu.
Delay line cancellerjest filtrem, który eliminuje składowe DC sygnałów echa odbieranych od nieruchomych celów. Oznacza to, że dopuszcza składowe AC sygnałów echa odbieranych od celów niestacjonarnych, tj. Celów ruchomych.
Rodzaje kasowników opóźniających
Kasowniki linii opóźniającej można podzielić na następujące two types na podstawie liczby znajdujących się w nim linii opóźniających.
- Pojedyncza linia opóźniająca
- Double Delay Line Canceller
W kolejnych sekcjach omówimy więcej na temat tych dwóch przerywaczy linii opóźnienia.
Pojedyncza linia opóźniająca
Połączenie linii opóźniającej i odejmowania jest znane jako kasownik linii opóźniającej. Nazywa się to również kasowaniem pojedynczej linii opóźnienia. Plikblock diagram odbiornika MTI z pojedynczym kasownikiem linii opóźniającej pokazano na poniższym rysunku.
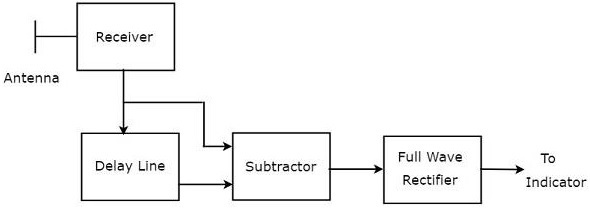
Możemy napisać mathematical equation odebranego sygnału echa po efekcie Dopplera jako -
$$ V_1 = A \ sin \ left [2 \ pi f_dt- \ phi_0 \ right] \: \: \: \: \: Równanie \: 1 $$
Gdzie,
A to amplituda sygnału wideo
$ f_d $ to częstotliwość Dopplera
$ \ phi_o $ to przesunięcie fazowe i jest równe $ 4 \ pi f_tR_o / C $
Otrzymamy output of Delay line canceller, zastępując $ t $ przez $ t-T_P $ w równaniu 1.
$$ V_2 = A \ sin \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right] \: \: \: \: \: Równanie \: 2 $$
Gdzie,
$ T_P $ to czas powtarzania impulsu
Otrzymamy subtractor output odejmując równanie 2 od równania 1.
$$ V_1-V_2 = A \ sin \ left [2 \ pi f_dt- \ phi_0 \ right] -A \ sin \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right] $$
$$ \ Rightarrow V_1-V_2 = 2A \ sin \ left [\ frac {2 \ pi f_dt- \ phi_0- \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right]} {2 } \ right] \ cos \ left [\ frac {2 \ pi f_dt- \ phi_o + 2 \ pi f_d \ left (t-T_P \ right) - \ phi_0} {2} \ right] $$
$$ V_1-V_2 = 2A \ sin \ left [\ frac {2 \ pi f_dT_P} {2} \ right] \ cos \ left [\ frac {2 \ pi f_d \ left (2t-T_P \ right) -2 \ phi_0} {2} \ right] $$
$$ \ Rightarrow V_1-V_2 = 2A \ sin \ left [\ pi f_dT_p \ right] \ cos \ left [2 \ pi f_d \ left (t- \ frac {T_P} {2} \ right) - \ phi_0 \ right ] \: \: \: \: \: Równanie \: 3 $$
Wyjście odejmowania jest stosowane jako wejście do prostownika pełnookresowego. Dlatego wyjście prostownika pełnookresowego wygląda tak, jak pokazano na poniższym rysunku. To nic innego jakfrequency response pojedynczej linii opóźniającej.

Z równania 3 możemy zauważyć, że odpowiedź częstotliwościowa kasety pojedynczej linii opóźniającej wynosi zero, gdy $ \ pi f_dT_P $ jest równe integer multiples of $ \ pi $ Oznacza to, że $ \ pi f_dT_P $ jest równe $ n \ pi $ Matematycznie można to zapisać jako
$$ \ pi f_dT_P = n \ pi $$
$$ \ Rightarrow f_dT_P = n $$
$$ \ Rightarrow f_d = \ frac {n} {T_P} \: \: \: \: \: Równanie \: 4 $$
Z równania 4 możemy wywnioskować, że odpowiedź częstotliwościowa tłumika pojedynczej linii opóźniającej osiąga zero, gdy częstotliwość Dopplera $ f_d $ jest równa całkowitej wielokrotności odwrotności czasu powtarzania impulsu $ T_P $.
Znamy następującą zależność między czasem powtarzania impulsów a częstotliwością powtarzania impulsów.
$$ f_d = \ frac {1} {T_P} $$
$$ \ Rightarrow \ frac {1} {T_P} = f_P \: \: \: \: \: Równanie \: 5 $$
Otrzymamy następujące równanie, zastępując równanie 5 w równaniu 4.
$$ \ Rightarrow f_d = nf_P \: \: \: \: \: Równanie \: 6 $$
Z Równania 6 możemy wywnioskować, że odpowiedź częstotliwościowa tłumika pojedynczej linii opóźniającej wynosi zero, gdy częstotliwość Dopplera $ f_d $ jest równa całkowitej wielokrotności częstotliwości powtarzania impulsów $ f_P $.
Blind Speeds
Z tego, czego się do tej pory dowiedzieliśmy, pojedyncza linia opóźniająca eliminuje składowe DC sygnałów echa odbieranych od nieruchomych celów, gdy $ n $ jest równe zero. Oprócz tego eliminuje również składowe AC sygnałów echa odbieranych od celów niestacjonarnych, gdy częstotliwość Dopplera $ f_d $ jest równa liczbie całkowitej(other than zero) wielokrotności częstotliwości powtarzania impulsów $ f_P $.
Tak więc, nazywane są prędkości względne, dla których odpowiedź częstotliwościowa tłumika pojedynczej linii opóźniającej osiąga zero blind speeds. Matematycznie możemy zapisać wyrażenie określające prędkość ślepą $ v_n $ jako -
$$ v_n = \ frac {n \ lambda} {2T_P} \: \: \: \: \: Równanie \: 7 $$
$$ \ Rightarrow v_n = \ frac {n \ lambda f_P} {2} \: \: \: \: \: Równanie \: 8 $$
Gdzie,
$ n $ jest liczbą całkowitą równą 1, 2, 3 i tak dalej
$ \ lambda $ to operacyjna długość fali
Przykładowy problem
Radar MTI działa z częstotliwością 6 $ GHZ $ z częstotliwością powtarzania impulsów 1 $ KHZ $. Znajdź pierwszą, drugą i trzeciąblind speeds tego radaru.
Rozwiązanie
Dany,
Częstotliwość robocza radaru MTI, $ f = 6GHZ $
Częstotliwość powtarzania impulsów, $ f_P = 1KHZ $.
Poniżej znajduje się wzór na operating wavelength $ \ lambda $ w zakresie częstotliwości roboczej, f.
$$ \ lambda = \ frac {C} {f} $$
Podstawmy, $ C = 3 \ times10 ^ 8m / sec $ i $ f = 6GHZ $ w powyższym równaniu.
$$ \ lambda = \ frac {3 \ times10 ^ 8} {6 \ times10 ^ 9} $$
$$ \ Rightarrow \ lambda = 0,05 mln $$
Tak więc operating wavelength $ \ lambda $ jest równe 0,05 mln $, gdy częstotliwość robocza f wynosi 6GHZ $.
Wiemy, co następuje formula for blind speed.
$$ v_n = \ frac {n \ lambda f_p} {2} $$
Podstawiając $ n $ = 1,2 i 3 w powyższym równaniu, otrzymamy następujące równania odpowiednio dla prędkości pierwszej, drugiej i trzeciej ślepej.
$$ v_1 = \ frac {1 \ times \ lambda f_p} {2} = \ frac {\ lambda f_p} {2} $$
$$ v_2 = \ frac {2 \ times \ lambda f_p} {2} = 2 \ left (\ frac {\ lambda f_p} {2} \ right) = 2v_1 $$
$$ v_3 = \ frac {3 \ times \ lambda f_p} {2} = 3 \ left (\ frac {\ lambda f_p} {2} \ right) = 3v_1 $$
Substitute wartości $ \ lambda $ i $ f_P $ w równaniu pierwszej prędkości ślepej.
$$ v_1 = \ frac {0.05 \ times 10 ^ 3} {2} $$
$$ \ Rightarrow v_1 = 25 m / s $$
Dlatego też first blind speed $ v_1 $ jest równe 25 mln USD / s $ dla podanych specyfikacji.
Otrzymamy wartości second & third blind speeds odpowiednio 50 mln $ / sek. i 75 mln $ / sek. $, zastępując wartość 1 w równaniach prędkości drugiej i trzeciej ciemnej.
Double Delay Line Canceller
Wiemy, że pojedynczy kasownik linii opóźniającej składa się z linii opóźniającej i odejmowania. Jeśli dwa takie separatory linii opóźniającej są połączone kaskadowo, wówczas ta kombinacja nazywana jest kasownikiem podwójnej linii opóźniającej. Plikblock diagram na poniższym rysunku pokazano kasownik z podwójną linią opóźniającą.

Niech $ p \ left (t \ right) $ i $ q \ left (t \ right) $ będą wejściem i wyjściem pierwszego kasowania linii opóźnienia. Otrzymamy następującą zależność matematyczną zfirst delay line canceller.
$$ q \ left (t \ right) = p \ left (t \ right) -p \ left (t-T_P \ right) \: \: \: \: \: Równanie \: 9 $$
Wyjście pierwszego kasownika linii opóźniającej jest stosowane jako wejście do drugiego kasownika linii opóźniającej. Stąd $ q \ left (t \ right) $ będzie wejściem kasownika drugiej linii opóźnienia. Niech $ r \ left (t \ right) $ będzie wyjściem kasety drugiej linii opóźnienia. Otrzymamy następującą relację matematyczną zsecond delay line canceller.
$$ r \ left (t \ right) = q \ left (t \ right) -q \ left (t-T_P \ right) \: \: \: \: \: Równanie \: 10 $$
Zastąp $ t $ przez $ t-T_P $ w równaniu 9.
$$ q \ left (t-T_P \ right) = p \ left (t-T_P \ right) -p \ left (t-T_P-T_P \ right) $$
$$ q \ left (t-T_P \ right) = p \ left (t-T_P \ right) -p \ left (t-2T_P \ right) \: \: \: \: \: Równanie \: 11 $$
Substitute, Równanie 9 i Równanie 11 w równaniu 10.
$$ r \ left (t \ right) = p \ left (t \ right) -p \ left (t-T_P \ right) - \ left [p \ left (t-T_P \ right) -p \ left (t -2T_P \ right) \ right] $$
$$ \ Rightarrow r \ left (t \ right) = p \ left (t \ right) -2p \ left (t-T_P \ right) + p \ left (t-2T_P \ right) \: \: \: \ : \: Równanie \: 12 $$
Plik advantagePodwójny tłumik linii opóźniających polega na tym, że szeroko odrzuca bałagan. Sygnał wyjściowy dwóch przerywaczy linii opóźniającej, które są połączone kaskadowo, będzie równy kwadratowi wyjścia kasownika pojedynczej linii opóźniającej.
Zatem wielkość sygnału wyjściowego tłumika podwójnej linii opóźniającej, która jest obecna w odbiorniku radarowym MTI, będzie równa 4 $ A ^ 2 \ left (\ sin \ left [\ pi f_dT_P \ right] \ right) ^ 2 $.

Charakterystyka odpowiedzi częstotliwościowej zarówno tłumika z podwójną linią opóźniającą, jak i kaskadowej kombinacji dwóch tłumików linii opóźniającej jest taka sama. Plikadvantage tłumika linii opóźnienia w dziedzinie czasu polega na tym, że może on działać we wszystkich zakresach częstotliwości.