SymPy - Szybki przewodnik

SymPy to biblioteka Pythona do wykonywania obliczeń symbolicznych. To jestcomputer algebra system(CAS), która może być używana jako samodzielna aplikacja lub jako biblioteka dla innych aplikacji. Jego sesja na żywo jest również dostępna pod adresemhttps://live.sympy.org/. Ponieważ jest to czysta biblioteka Pythona, może być używana jako tryb interaktywny i jako aplikacja programowa. SymPy stało się obecnie popularną biblioteką symboli dla naukowego ekosystemu Pythona.

SymPy posiada szeroką gamę funkcji mających zastosowanie w zakresie podstawowych arytmetyki symbolicznej, rachunku różniczkowego, algebry, matematyki dyskretnej, fizyki kwantowej itp. SymPy jest w stanie formatować wyniki w różnych formatach, w tym LaTeX, MathML itp. SymPy jest dystrybuowany pod Nowa licencja BSD. Zespół programistów pod kierownictwemOndřej Čertík i Aaron Meurer opublikował pierwszą wersję SymPy w 2007 roku. Obecna wersja to 1.5.1.

Niektóre obszary zastosowań SymPy to -

Polynomials
Calculus
Dyskretne matematyki
Matrices
Geometry
Plotting
Physics
Statistics
Combinatorics

SymPy ma jedną ważną bibliotekę wymagań wstępnych o nazwie mpmath. Jest to biblioteka Pythona do rzeczywistej i złożonej arytmetyki zmiennoprzecinkowej z dowolną precyzją. Jednak PIP instalator pakietów Pythona instaluje go automatycznie po zainstalowaniu SymPy w następujący sposób -

pip install sympy

Inne dystrybucje Pythona, takie jak Anaconda, Enthought Canopy itp., Mogą mieć już dołączone oprogramowanie SymPy. Aby zweryfikować, możesz wpisać następujące polecenie w zachęcie Pythona -

>>> import sympy
>>> sympy.__version__

Otrzymasz poniższe dane wyjściowe jako aktualną wersję sympy -

'1.5.1'

Kod źródłowy pakietu SymPy jest dostępny pod adresem https://github.com/sympy/sympy.

Obliczenia symboliczne odnoszą się do opracowywania algorytmów manipulowania wyrażeniami matematycznymi i innymi obiektami matematycznymi. Obliczenia symboliczne integrują matematykę z informatyką, aby rozwiązywać wyrażenia matematyczne za pomocą symboli matematycznych. System algebry komputerowej (CAS), taki jak SymPy, oblicza wyrażenia algebraiczne dokładnie (nie w przybliżeniu) przy użyciu tych samych symboli, które są używane w tradycyjnej metodzie ręcznej. Na przykład obliczamy pierwiastek kwadratowy z liczby za pomocą modułu matematycznego Pythona, jak podano poniżej -

>>> import math 
>>> print (math.sqrt(25), math.sqrt(7))

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

5.0 2.6457513110645907

Jak widać, w przybliżeniu obliczany jest pierwiastek kwadratowy z 7. Ale w SymPy pierwiastki kwadratowe liczb, które nie są idealnymi kwadratami, są domyślnie nieocenione, jak podano poniżej -

>>> import sympy 
>>> print (sympy.sqrt(7))

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

sqrt(7)

Możliwe jest uproszczenie i symboliczne przedstawienie wyniku wyrażenia za pomocą poniższego fragmentu kodu -

>>> import math
>>> print (math.sqrt(12))

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

3.4641016151377544

Musisz użyć poniższego fragmentu kodu, aby wykonać to samo za pomocą sympy -

##sympy output 
>>> print (sympy.sqrt(12))

Wynik tego jest następujący -

2*sqrt(3)

Kod SymPy, po uruchomieniu w notatniku Jupyter, wykorzystuje bibliotekę MathJax do renderowania symboli matematycznych w postaci LatEx. Jest to pokazane w poniższym fragmencie kodu -

>>> from sympy import * 
>>> x=Symbol ('x') 
>>> expr = integrate(x**x, x) 
>>> expr

Po wykonaniu powyższego polecenia w powłoce Pythona wygenerowane zostaną następujące dane wyjściowe -

Integral(x**x, x)

Co jest równoważne

$\int \mathrm{x}^{x}\,\mathrm{d}x$

Pierwiastek kwadratowy z niedoskonałego kwadratu można przedstawić za pomocą lateksu w następujący sposób za pomocą tradycyjnego symbolu -

>>> from sympy import * 
>>> x=7 
>>> sqrt(x)

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

$\sqrt7$

Symboliczny system obliczeniowy, taki jak SymPy, wykonuje wszystkie rodzaje obliczeń (takich jak pochodne, całki i granice, rozwiązuje równania, pracuje z macierzami). Pakiet SymPy posiada różne moduły obsługujące kreślenie, drukowanie (jak LATEX), fizykę, statystykę, kombinatorykę, teorię liczb, geometrię, logikę itp.

Podstawowy moduł pakietu SymPy zawiera klasę Number, która reprezentuje liczby atomowe. Ta klasa ma dwie podklasy: Float i Rational. Klasa wymierna jest dodatkowo rozszerzona o klasę Integer.

Klasa zmiennoprzecinkowa reprezentuje liczbę zmiennoprzecinkową o dowolnej precyzji.

>>> from sympy import Float 
>>> Float(6.32)

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

6.32

SymPy może konwertować liczbę całkowitą lub ciąg znaków na zmiennoprzecinkowe.

>>> Float(10)

10.0

Float('1.33E5')# scientific notation

133000.0

Podczas konwersji na zmiennoprzecinkowe można również określić liczbę cyfr dla dokładności, jak podano poniżej -

>>> Float(1.33333,2)

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

1.3

Reprezentacja liczby (p / q) jest reprezentowana jako obiekt klasy Rational, gdzie q jest liczbą niezerową.

>>> Rational(3/4)

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

$\frac{3}{4}$

Jeśli liczba zmiennoprzecinkowa zostanie przekazana do konstruktora Rational (), zwraca podstawową wartość swojej reprezentacji binarnej

>>> Rational(0.2)

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

$\frac{3602879701896397}{18014398509481984}$

Aby uzyskać prostszą reprezentację, określ ograniczenie mianownika.

>>> Rational(0.2).limit_denominator(100)

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

$\frac{1}{5}$

Gdy łańcuch jest przekazywany do konstruktora Rational (), zwracana jest wymierna liczba o dowolnej precyzji.

>>> Rational("3.65")

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

$\frac{73}{20}$

Obiekt wymierny można również uzyskać, przekazując dwa argumenty liczbowe. Części licznika i mianownika są dostępne jako właściwości.

>>> a=Rational(3,5) 
>>> print (a) 
>>> print ("numerator:{}, denominator:{}".format(a.p, a.q))

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

3/5

numerator:3, denominator:5

>>> a

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

$\frac{3}{5}$

Klasa Integer w SymPy reprezentuje liczbę całkowitą o dowolnej wielkości. Konstruktor może akceptować liczbę zmiennoprzecinkową lub wymierną, ale część ułamkowa jest odrzucana

>>> Integer(10)

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

>>> Integer(3.4)

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

>>> Integer(2/7)

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

SymPy ma RealNumberklasa, która działa jako alias dla Float. SymPy definiuje również Zero i One jako klasy pojedyncze dostępne odpowiednio z S.Zero i S.One, jak pokazano poniżej -

>>> S.Zero

Dane wyjściowe są następujące -

>>> S.One

Dane wyjściowe są następujące -

Inne predefiniowane obiekty liczb singletonów to Half, NaN, Infinity i ImaginaryUnit

>>> from sympy import S 
>>> print (S.Half)

Dane wyjściowe są następujące -

>>> print (S.NaN)

Dane wyjściowe są następujące -

nan

Infinity jest dostępne jako obiekt symbolu oo lub S.Infinity

>>> from sympy import oo 
>>> oo

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

$\infty$

>>> S.Infinity

Dane wyjściowe dla powyższego fragmentu kodu są następujące -

$\infty$

Liczba ImaginaryUnit może być importowana jako symbol I lub dostępna jako S.ImaginaryUnit i reprezentuje pierwiastek kwadratowy z -1

>>> from sympy import I 
>>> I

Po wykonaniu powyższego fragmentu kodu otrzymasz następujące dane wyjściowe -

>>> S.ImaginaryUnit

Wynik powyższego fragmentu kodu jest następujący -

>>> from sympy import sqrt 
>>> i=sqrt(-1) 
>>> i*i

Po wykonaniu powyższego fragmentu kodu otrzymasz następujące dane wyjściowe -

-1

Symboljest najważniejszą klasą w bibliotece symPy. Jak wspomniano wcześniej, obliczenia symboliczne są wykonywane za pomocą symboli. Zmienne SymPy są obiektami klasy Symbols.

Argumentem funkcji Symbol () jest łańcuch zawierający symbol, który można przypisać do zmiennej.

>>> from sympy import Symbol 
>>> x=Symbol('x') 
>>> y=Symbol('y') 
>>> expr=x**2+y**2 
>>> expr

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x^2 + y^2$

Symbol może składać się z więcej niż jednego alfabetu.

>>> s=Symbol('side') 
>>> s**3

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$side^3$

SymPy ma również plik Symbols()funkcja, która może definiować wiele symboli jednocześnie. Ciąg zawiera nazwy zmiennych oddzielone przecinkiem lub spacją.

>>> from sympy import symbols 
>>> x,y,z=symbols("x,y,z")

W module abc SymPy wszystkie alfabety łacińskie i greckie są zdefiniowane jako symbole. Dlatego zamiast tworzenia wystąpienia obiektu Symbol ta metoda jest wygodna.

>>> from sympy.abc import x,y,z

Jednak nazwy C, O, S, I, N, E i Qto predefiniowane symbole. Ponadto symbole z więcej niż jednym alfabetem nie są zdefiniowane w module abc, dla którego należy używać obiektu Symbol jak powyżej. Moduł abc definiuje specjalne nazwy, które mogą wykrywać definicje w domyślnej przestrzeni nazw SymPy. clash1 zawiera pojedyncze litery, a clash2 ma wieloliterowe symbole kolizji

>>> from sympy.abc import _clash1, _clash2 
>>> _clash1

Wynik powyższego fragmentu kodu jest następujący -

{'C': C, 'O': O, 'Q': Q, 'N': N, 'I': I, 'E': E, 'S': S}

>>> _clash2

Wynik powyższego fragmentu kodu jest następujący -

{'beta': beta, 'zeta': zeta, 'gamma': gamma, 'pi': pi}

Symbole indeksowane można zdefiniować za pomocą składni podobnej do funkcji range (). Zakresy są oznaczone dwukropkiem. Typ zakresu jest określany przez znak po prawej stronie dwukropka. Jeśli itr jest cyfrą, wszystkie ciągłe cyfry po lewej stronie są traktowane jako nieujemna wartość początkowa. Wszystkie ciągłe cyfry po prawej stronie są traktowane jako o 1 większe od wartości końcowej.

>>> from sympy import symbols 
>>> symbols('a:5')

Wynik powyższego fragmentu kodu jest następujący -

(a0, a1, a2, a3, a4)

>>> symbols('mark(1:4)')

Wynik powyższego fragmentu kodu jest następujący -

(mark1, mark2, mark3)

Jedną z najbardziej podstawowych operacji wykonywanych na wyrażeniu matematycznym jest podstawianie. Funkcja subs () w SymPy zastępuje wszystkie wystąpienia pierwszego parametru drugim.

>>> from sympy.abc import x,a 
>>> expr=sin(x)*sin(x)+cos(x)*cos(x) 
>>> expr

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\sin^2(x)+\cos^2(x)$

>>> expr.subs(x,a)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\sin^2(a)+\cos^2(a)$

Ta funkcja jest przydatna, jeśli chcemy ocenić określone wyrażenie. Na przykład chcemy obliczyć wartości następującego wyrażenia, zastępując a przez 5.

>>> expr=a*a+2*a+5 
>>> expr

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$a^2 + 2a + 5$

expr.subs(a,5)

Powyższy fragment kodu daje następujące dane wyjściowe -

>>> from sympy.abc import x 
>>> from sympy import sin, pi 
>>> expr=sin(x) 
>>> expr1=expr.subs(x,pi) 
>>> expr1

Powyższy fragment kodu daje następujące dane wyjściowe -

Ta funkcja służy również do zastępowania wyrażenia podrzędnego innym wyrażeniem podrzędnym. W poniższym przykładzie b jest zastąpione przez a + b.

>>> from sympy.abc import a,b 
>>> expr=(a+b)**2 
>>> expr1=expr.subs(b,a+b) 
>>> expr1

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$(2a + b)^2$

Funkcja sympify () służy do konwersji dowolnego dowolnego wyrażenia, tak aby można go było używać jako wyrażenia SymPy. Normalne obiekty Pythona, takie jak obiekty typu integer, są konwertowane w SymPy. Ciągi liczb całkowitych itp. Są również konwertowane na wyrażenia SymPy.

>>> expr="x**2+3*x+2" 
>>> expr1=sympify(expr) 
>>> expr1 
>>> expr1.subs(x,2)

Powyższy fragment kodu daje następujące dane wyjściowe -

Każdy obiekt Pythona można przekonwertować w obiekcie SymPy. Jednakże, ponieważ konwersja wewnętrznie wykorzystuje funkcję eval (), nie powinno się używać wyrażenia nonanitized, w przeciwnym razie zostanie zgłoszony SympifyError.

>>> sympify("x***2")
---------------------------------------------------------------------------

SympifyError: Sympify wyrażenia „nie można przeanalizować” x *** 2 ”nie powiodło się z powodu zgłaszania wyjątku.

Funkcja sympify () przyjmuje następujące argumenty: * strict: domyślnie False. W przypadku ustawienia wartości True konwertowane są tylko typy, dla których zdefiniowano jawną konwersję. W przeciwnym razie zostanie zgłoszony SympifyError. * ewaluacja: Jeśli ustawiona na False, arytmetyka i operatory zostaną przekonwertowane na ich odpowiedniki SymPy bez oceny wyrażenia.

>>> sympify("10/5+4/2")

Powyższy fragment kodu daje następujące dane wyjściowe -

>>> sympify("10/5+4/2", evaluate=False)

Powyższy fragment kodu daje następujące dane wyjściowe -

$\frac{10}{5}+\frac{4}{2}$

Ta funkcja oblicza dane wyrażenie liczbowe do określonej dokładności zmiennoprzecinkowej do 100 cyfr. Funkcja pobiera również parametr subs jako obiekt słownikowy wartości liczbowych dla symboli. Rozważ następujące wyrażenie

>>> from sympy.abc import r 
>>> expr=pi*r**2 
>>> expr

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\Pi{r^2}$

Aby ocenić powyższe wyrażenie za pomocą funkcji evalf (), zastępując r przez 5

>>> expr.evalf(subs={r:5})

Powyższy fragment kodu daje następujące dane wyjściowe -

78.5398163397448

Domyślnie precyzja zmiennoprzecinkowa wynosi maksymalnie 15 cyfr, które mogą być nadpisane dowolną liczbą do 100. Następujące wyrażenie jest szacowane z dokładnością do 20 cyfr.

>>> expr=a/b 
>>> expr.evalf(20, subs={a:100, b:3})

Powyższy fragment kodu daje następujące dane wyjściowe -

33.333333333333333333

Funkcja lambdify tłumaczy wyrażenia SymPy na funkcje Pythona. Jeśli wyrażenie ma być oceniane w szerokim zakresie wartości, funkcja evalf () nie jest wydajna. lambdify działa jak funkcja lambda, z tą różnicą, że konwertuje nazwy SymPy na nazwy podanej biblioteki numerycznej, zwykle NumPy. Domyślnie lambdify na implementacjach w standardowej bibliotece matematycznej.

>>> expr=1/sin(x) 
>>> f=lambdify(x, expr) 
>>> f(3.14)

Powyższy fragment kodu daje następujące dane wyjściowe -

627.8831939138764

Wyrażenie może mieć więcej niż jedną zmienną. W takim przypadku pierwszym argumentem funkcji lambdify () jest lista zmiennych, po której następuje wyrażenie, które ma zostać ocenione.

>>> expr=a**2+b**2 
>>> f=lambdify([a,b],expr) 
>>> f(2,3)

Powyższy fragment kodu daje następujące dane wyjściowe -

Jednak aby wykorzystać bibliotekę numpy jako zaplecze numeryczne, musimy zdefiniować to samo jako argument funkcji lambdify ().

>>> f=lambdify([a,b],expr, "numpy")

Używamy dwóch tablic numpy dla dwóch argumentów a i b w powyższej funkcji. Czas wykonania jest znacznie szybki w przypadku tablic numpy.

>>> import numpy 
>>> l1=numpy.arange(1,6) 
>>> l2=numpy.arange(6,11) 
>>> f(l1,l2)

Powyższy fragment kodu daje następujące dane wyjściowe -

array([ 37, 53, 73, 97, 125], dtype=int32)

Funkcje boolowskie są zdefiniowane w sympy.basic.booleanarg module. Możliwe jest budowanie wyrażeń boolowskich za pomocą standardowych operatorów Pythona & (And), | (Lub), ~ (Nie), a także z >> i <<. Wyrażenia logiczne dziedziczą z klasy Basic zdefiniowanej w podstawowym module SymPy.

Funkcja BooleanTrue

Ta funkcja jest odpowiednikiem True, tak jak w rdzeniu Pythona. Zwraca singleton, który może pobrać S.true.

>>> from sympy import * 
>>> x=sympify(true) 
>>> x, S.true

Powyższy fragment kodu daje następujące dane wyjściowe -

(Prawda, prawda)

Funkcja BooleanFalse

Podobnie, ta funkcja jest odpowiednikiem Boolean False w Pythonie i może być dostępna przez S.false

>>> from sympy import * 
>>> x=sympify(false) 
>>> x, S.false

Powyższy fragment kodu daje następujące dane wyjściowe -

(Fałsz, Fałsz)

I funkcjonować

Funkcja logiczna AND oblicza swoje dwa argumenty i zwraca wartość False, jeśli którykolwiek z nich jest false. Funkcja emuluje & operator.

>>> from sympy import * 
>>> from sympy.logic.boolalg import And 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=True 
>>> And(x,y), x"&"y

Powyższy fragment kodu daje następujące dane wyjściowe -

(Prawda, prawda)

>>> y=False 
>>> And(x,y), x"&"y

Powyższy fragment kodu daje następujące dane wyjściowe -

(Fałsz, Fałsz)

Albo funkcjonować

Ta funkcja oblicza dwa argumenty logiczne i zwraca wartość True, jeśli którykolwiek z nich ma wartość True. | operator wygodnie naśladuje jego zachowanie.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Or 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False 
>>> Or(x,y), x|y

Powyższy fragment kodu daje następujące dane wyjściowe -

(Prawda, prawda)

>>> x=False 
>>> y=False 
>>> Or(x,y), x|y

Powyższy fragment kodu daje następujące dane wyjściowe -

(Fałsz, Fałsz)

Nie działa

Funkcja Logical Not powoduje negację argumentu boolowskiego. Zwraca True, jeśli jego argument jest False i zwraca False, jeśli True. Operator ~ wykonuje operację podobną do funkcji Not. Pokazuje to poniższy przykład -

>>> from sympy import * 
>>> from sympy.logic.boolalg import Or, And, Not 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False 
>>> Not(x), Not(y)

Powyższy fragment kodu daje następujące dane wyjściowe -

(Fałsz PRAWDA)

>>> Not(And(x,y)), Not(Or(x,y))

Powyższy fragment kodu daje następujące dane wyjściowe -

(Prawda fałsz)

Funkcja Xor

Funkcja Logical XOR (wyłączne LUB) zwraca wartość True, jeśli nieparzysta liczba argumentów to True, a reszta to False, i zwraca False, jeśli parzysta liczba argumentów to True, a reszta to False. Podobną operację wykonuje operator ^.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Xor 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False

>>> Xor(x,y), x^y

Powyższy fragment kodu daje następujące dane wyjściowe -

(Prawda, prawda)

>>> a,b,c,d,e=symbols('a b c d e') 
>>> a,b,c,d,e=(True, False, True, True, False) 
>>> Xor(a,b,c,d,e)

Powyższy fragment kodu daje następujące dane wyjściowe -

Prawdziwe

W powyższym przypadku trzy (nieparzyste) argumenty mają wartość True, dlatego Xor zwraca wartość true. Jeśli jednak liczba argumentów True jest parzysta, skutkuje to False, jak pokazano poniżej -

>>> a,b,c,d,e=(True, False, False, True, False) 
>>> Xor(a,b,c,d,e)

Powyższy fragment kodu daje następujące dane wyjściowe -

Fałszywy

Funkcja Nand

Ta funkcja wykonuje operację logiczną NAND. Ocenia swoje argumenty i zwraca True, jeśli którykolwiek z nich jest False, i False, jeśli wszystkie są True.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Nand 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Nand(a,b,c), Nand(a,c)

Powyższy fragment kodu daje następujące dane wyjściowe -

(Prawda fałsz)

Ani funkcja

Ta funkcja wykonuje operację logiczną NOR. Ocenia swoje argumenty i zwraca False, jeśli którykolwiek z nich jest True, i True, jeśli wszystkie są False.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Nor 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Nor(a,b,c), Nor(a,c)

Powyższy fragment kodu daje następujące dane wyjściowe -

(Fałsz, Fałsz)

Zauważ, że chociaż SymPy zapewnia operator ^ dla Xor, ~ dla Not, | dla funkcji Or i & dla I jako wygody, ich normalne użycie w Pythonie to operatory bitowe. Stąd, jeśli operandy są liczbami całkowitymi, wyniki byłyby inne.

Funkcja równoważna

Ta funkcja zwraca relację równoważności. Równoważnik (A, B) jest Prawdą wtedy i tylko wtedy, gdy A i B są zarówno Prawdą, jak i Fałszem. Funkcja zwraca True, jeśli wszystkie argumenty są logicznie równoważne. W przeciwnym razie zwraca wartość False.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Equivalent 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Equivalent(a,b), Equivalent(a,c)

Powyższy fragment kodu daje następujące dane wyjściowe -

(Fałsz PRAWDA)

Funkcja ITE

Ta funkcja działa jak klauzula If then else w języku programowania .ITE (A, B, C) oblicza i zwraca wynik B, jeśli A jest prawdziwe, w przeciwnym razie zwraca wynik C. Wszystkie argumenty muszą być wartościami logicznymi.

>>> from sympy import * >>> from sympy.logic.boolalg import ITE >>> a,b,c=symbols('a b c') >>> a,b,c=(True, False, True) 
>>> ITE(a,b,c), ITE(a,c,b)

Powyższy fragment kodu daje następujące dane wyjściowe -

(Fałsz PRAWDA)

Moduł założeń w pakiecie SymPy zawiera narzędzia do wydobywania informacji o wyrażeniach. W tym celu moduł definiuje funkcję ask ().

sympy.assumptions.ask(property)

Poniższe właściwości zawierają przydatne informacje o wyrażeniu -

algebraic(x)

Aby liczba była algebraiczna, musi być pierwiastkiem niezerowego równania wielomianowego z wymiernymi współczynnikami. √2, ponieważ √2 jest rozwiązaniem x2 - 2 = 0, więc jest algebraiczne.

complex(x)

Predykat liczb zespolonych. Jest prawdą wtedy i tylko wtedy, gdy x należy do zbioru liczb zespolonych.

composite(x)

Predykat liczby złożonej zwracany przez ask (Q.composite (x)) jest prawdziwy wtedy i tylko wtedy, gdy x jest dodatnią liczbą całkowitą i ma co najmniej jeden dodatni dzielnik inny niż 1 i samą liczbę.

even, odd

Funkcja ask () zwraca prawdę z x znajduje się odpowiednio w zbiorze liczb parzystych i zbiorze liczb nieparzystych.

imaginary

Ta właściwość reprezentuje predykat liczby urojonej. Prawdą jest, że x można zapisać jako liczbę rzeczywistą pomnożoną przez urojoną jednostkę I.

integer

Ta właściwość zwrócona przez Q.integer (x) zwraca true z x należy do zbioru liczb parzystych.

rational, irrational

Q.irrational (x) jest prawdą wtedy i tylko wtedy, gdy x jest dowolną liczbą rzeczywistą, której nie można wyrazić jako stosunek liczb całkowitych. Na przykład liczba pi jest liczbą niewymierną.

positive, negative

Predykaty sprawdzające, czy liczba jest dodatnia czy ujemna

zero, nonzero

Predykaty do cholery, czy liczba jest równa zero, czy nie

>>> from sympy import * 
>>> x=Symbol('x') 
>>> x=10 
>>> ask(Q.algebraic(pi))
False
>>> ask(Q.complex(5-4*I)), ask( Q.complex(100))
(True, True)
>>> x,y=symbols("x y") 
>>> x,y=5,10 
>>> ask(Q.composite(x)), ask(Q.composite(y))
(False, True)
>>> ask(Q.even(x)), ask(Q.even(y))
(False, True)
>>> x,y= 2*I, 4+5*I 
>>> ask(Q.imaginary(x)), ask(Q.imaginary(y))
(True, False)
>>> x,y=5,10 
>>> ask(Q.even(x)), ask(Q.even(y)), ask(Q.odd(x)), ask(Q.odd(y))
(False, True, True, False)
>>> x,y=5,-5 
>>> ask(Q.positive(x)), ask(Q.negative(y)), ask(Q.positive(x)), ask(Q.negative(y))
(True, True, True, True)
>>> ask(Q.rational(pi)), ask(Q.irrational(S(2)/3))
(False, False)
>>> ask(Q.zero(oo)), ask(Q.nonzero(I))
(False, False)

Sympy ma potężną zdolność upraszczania wyrażeń matematycznych. W SymPy jest wiele funkcji służących do różnych uproszczeń. Istnieje ogólna funkcja o nazwie simplify (), która próbuje dojść do najprostszej formy wyrażenia.

uproszczać

Ta funkcja jest zdefiniowana w module sympy.simplify. simplify () próbuje zastosować inteligentną heurystykę, aby wyrażenie wejściowe było „prostsze”. Poniższy kod przedstawia upraszcza wyrażenie$sin^2(x)+cos^2(x)$.

>>> from sympy import * 
>>> x=Symbol('x')
>>> expr=sin(x)**2 + cos(x)**2 
>>> simplify(expr)

Powyższy fragment kodu daje następujące dane wyjściowe -

rozszerzać

Expand () jest jedną z najczęściej używanych funkcji upraszczających w SymPy, używaną do rozwijania wyrażeń wielomianowych. Na przykład -

>>> a,b=symbols('a b') 
>>> expand((a+b)**2)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$a^2 + 2ab + b^2$

>>> expand((a+b)*(a-b))

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$a^2 - b^2$

Funkcja expand () sprawia, że wyrażenia są większe, a nie mniejsze. Zwykle tak jest, ale często wyrażenie staje się mniejsze po wywołaniu na nim funkcji expand ().

>>> expand((x + 1)*(x - 2) - (x - 1)*x)

Powyższy fragment kodu daje następujące dane wyjściowe -

-2

czynnik

Ta funkcja przyjmuje wielomian i rozkłada go na czynniki nieredukowalne w liczbach wymiernych.

>>> x,y,z=symbols('x y z') 
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
>>> factor(expr)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$z(x + 2y)^2$

>>> factor(x**2+2*x+1)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$(x + 1)^2$

Funkcja factor () jest przeciwieństwem funkcji expand (). Każdy z czynników zwracanych przez factor () jest gwarantowany jako nieredukowalny. Funkcja factor_list () zwraca bardziej ustrukturyzowane dane wyjściowe.

>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
>>> factor_list(expr)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

(1, [(z, 1), (x + 2*y, 2)])

zbierać

Ta funkcja zbiera dodatkowe warunki wyrażenia w odniesieniu do listy wyrażeń aż do potęg z wymiernymi wykładnikami.

>>> expr=x*y + x - 3 + 2*x**2 - z*x**2 + x**3 
>>> expr

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x^3 + x^2z + 2x^2 + xy + x - 3$

Funkcja collect () w tym wyrażeniu daje następujące wyniki -

>>> collect(expr,x)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x^3 + x^2(2 - z) + x(y + 1) - 3$

>>> expr=y**2*x + 4*x*y*z + 4*y**2*z+y**3+2*x*y 
>>> collect(expr,y)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$Y^3+Y^2(x+4z)+y(4xz+2x)$

Anuluj

Funkcja cancel () przyjmie dowolną funkcję wymierną i umieści ją w standardowej formie kanonicznej p / q, gdzie p i q są rozszerzonymi wielomianami bez wspólnych czynników. Wiodące współczynniki p i q nie mają mianowników, tj. Są liczbami całkowitymi.

>>> expr1=x**2+2*x+1 
>>> expr2=x+1 
>>> cancel(expr1/expr2)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x+1$

>>> expr = 1/x + (3*x/2 - 2)/(x - 4) 
>>> expr

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{\frac{3x}{2} - 2}{x - 4} + \frac{1}{x}$

>>> cancel(expr)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{3x^2 - 2x - 8}{2x^2 - 8}$

>>> expr=1/sin(x)**2 
>>> expr1=sin(x) 
>>> cancel(expr1*expr)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{1}{\sin(x)}$

trigsimp

Ta funkcja służy do uproszczenia tożsamości trygonometrycznych. Można zauważyć, że konwencją nazewnictwa dla odwrotnych funkcji trygonometrycznych jest dodanie litery a na początku nazwy funkcji. Na przykład odwrotny cosinus lub łuk cosinus nazywa się acos ().

>>> from sympy import trigsimp, sin, cos 
>>> from sympy.abc import x, y
>>> expr = 2*sin(x)**2 + 2*cos(x)**2 
>>> trigsimp(expr)

Funkcja trigsimp wykorzystuje heurystykę do zastosowania najlepiej dopasowanej tożsamości trygonometrycznej.

powersimp

Ta funkcja redukuje dane wyrażenie, łącząc potęgi o podobnych podstawach i wykładnikach.

>>> expr=x**y*x**z*y**z 
>>> expr

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x^y x^z y^z$

>>> powsimp(expr)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x^{y+z} y^z$

Możesz sprawić, że funkcja powsimp () będzie tylko łączyć zasady lub tylko łączyć wykładniki, zmieniając kombinację = 'podstawa' lub łączenie = 'exp'. Domyślnie, connect = 'all', co robi oba. Jeśli force ma wartość True, wtedy bazy zostaną połączone bez sprawdzania założeń.

>>> powsimp(expr, combine='base', force=True)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x^y(xy)^z$

grzebień

Wyrażenia kombinatoryczne obejmujące silnię i dwumiany można uprościć za pomocą funkcji combsimp (). SymPy udostępnia funkcję silnia ()

>>> expr=factorial(x)/factorial(x - 3) 
>>> expr

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{x!}{(x - 3)!}$

Aby uprościć powyższe wyrażenie kombinatoryczne, używamy funkcji combsimp () w następujący sposób -

>>> combsimp(expr)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x(x-2)(x-1)$

Dwumian (x, y) to liczba sposobów wyboru y elementów z zestawu x różnych elementów. Często jest również zapisywany jako xCy.

>>> binomial(x,y)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$(\frac{x}{y})$

>>> combsimp(binomial(x+1, y+1)/binomial(x, y))

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{x + 1}{y + 1}$

logcombine

Ta funkcja bierze logarytmy i łączy je, stosując następujące zasady -

log (x) + log (y) == log (x * y), jeśli oba są dodatnie
a * log (x) == log (x ** a) jeśli x jest dodatnie, a a jest rzeczywiste

>>> logcombine(a*log(x) + log(y) - log(z))

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$a\log(x) + \log(y) - \log(z)$

Jeśli parametr siły tej funkcji jest ustawiony na True, to powyższe założenia zostaną przyjęte, jeśli nie ma już założeń dotyczących ilości.

>>> logcombine(a*log(x) + log(y) - log(z), force=True)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\log\frac{x^a y}{z}$

Pochodna funkcji to chwilowa szybkość zmian jednej z jej zmiennych. Jest to równoznaczne ze znalezieniem nachylenia stycznej do funkcji w punkcie. Zróżnicowanie wyrażeń matematycznych w postaci zmiennych możemy znaleźć za pomocą funkcji diff () w pakiecie SymPy.

diff(expr, variable)
>>> from sympy import diff, sin, exp 
>>> from sympy.abc import x,y 
>>> expr=x*sin(x*x)+1 >>> expr

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x\sin(x^2) + 1$

>>> diff(expr,x)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$2x^2\cos(x^2) + \sin(x^2)$

>>> diff(exp(x**2),x)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

2xe^x²

Aby wziąć wiele pochodnych, podaj zmienną tyle razy, ile chcesz różnicować, lub podaj liczbę po zmiennej.

>>> diff(x**4,x,3)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$24x$

>>> for i in range(1,4): print (diff(x**4,x,i))

Powyższy fragment kodu zawiera poniższe wyrażenie -

4*x**3

12*x**2

24*x

Możliwe jest również wywołanie metody diff () wyrażenia. Działa podobnie jak funkcja diff ().

>>> expr=x*sin(x*x)+1 
>>> expr.diff(x)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$2x^2\cos(x^2) + \sin(x^2)$

Niedoszacowany instrument pochodny jest tworzony za pomocą klasy Instrument pochodny. Ma taką samą składnię jak funkcja diff (). Aby ocenić niedoszacowaną pochodną, użyj metody doit.

>>> from sympy import Derivative 
>>> d=Derivative(expr) 
>>> d

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{d}{dx}(x\sin(x^2)+1)$

>>> d.doit()

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$2x^2\cos(x^2) + \sin(x^2)$

Pakiet SymPy zawiera moduł całek. Implementuje metody obliczania całek oznaczonych i nieoznaczonych wyrażeń. Metoda integrate () służy do obliczania całek oznaczonych i nieoznaczonych. Aby obliczyć całkę nieokreśloną lub pierwotną, po prostu przekaż zmienną po wyrażeniu.

Na przykład -

integrate(f, x)

Aby obliczyć określoną całkę, przekaż argument w następujący sposób -

(integration_variable, lower_limit, upper_limit)

>>> from sympy import * 
>>> x,y = symbols('x y') 
>>> expr=x**2 + x + 1 
>>> integrate(expr, x)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{x^3}{3} + \frac{x^2}{2} + x$

>>> expr=sin(x)*tan(x) 
>>> expr 
>>> integrate(expr,x)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$-\frac{\log(\sin(x) - 1)}{2} + \frac{\log(\sin(x) + 1)}{2} - \sin(x)$

Przykład całki oznaczonej podano poniżej -

>>> expr=exp(-x**2) 
>>> integrate(expr,(x,0,oo) )

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{\sqrt\pi}{2}$

Możesz przekazać wiele krotek limitów, aby wykonać całkę wielokrotną. Przykład podano poniżej -

>>> expr=exp(-x**2 - y**2)
>>> integrate(expr,(x,0,oo),(y,0,oo))

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{\pi}{4}$

Możesz utworzyć całkę nieocenioną za pomocą obiektu Integral, który można obliczyć, wywołując metodę doit ().

>>> expr = Integral(log(x)**2, x) 
>>> expr

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\int \mathrm\log(x)^2 \mathrm{d}x$

>>> expr.doit()

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x\log(x)^2 - 2xlog(x) + 2x$

Transformacje całkowe

SymPy obsługuje różne typy przekształceń całkowitych w następujący sposób -

laplace_transform
fourier_transform
sine_transform
cosine_transform
hankel_transform

Funkcje te są zdefiniowane w module sympy.integrals.transforms. Poniższe przykłady obliczają odpowiednio transformatę Fouriera i transformatę Laplace'a.

Example 1

>>> from sympy import fourier_transform, exp 
>>> from sympy.abc import x, k 
>>> expr=exp(-x**2) 
>>> fourier_transform(expr, x, k)

Po wykonaniu powyższego polecenia w powłoce Pythona wygenerowane zostaną następujące dane wyjściowe -

sqrt(pi)*exp(-pi**2*k**2)

Co jest równoważne -

$\sqrt\pi * e^{\pi^2k^2}$

Example 2

>>> from sympy.integrals import laplace_transform 
>>> from sympy.abc import t, s, a 
>>> laplace_transform(t**a, t, s)

Po wykonaniu powyższego polecenia w powłoce Pythona wygenerowane zostaną następujące dane wyjściowe -

(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)

W matematyce macierz to dwuwymiarowa tablica liczb, symboli lub wyrażeń. Teoria manipulacji macierzami zajmuje się wykonywaniem operacji arytmetycznych na obiektach macierzowych, podlegających pewnym regułom.

Transformacja liniowa jest jednym z ważnych zastosowań macierzy. Wiele dziedzin naukowych, szczególnie związanych z fizyką, wykorzystuje aplikacje związane z macierzami.

Pakiet SymPy posiada moduł macierzy zajmujący się obsługą macierzy. Zawiera klasę Matrix, której obiekt reprezentuje macierz.

Note: If you want to execute all the snippets in this chapter individually, you need to import the matrix module as shown below −

>>> from sympy.matrices import Matrix

Example

>>> from sympy.matrices import Matrix 
>>> m=Matrix([[1,2,3],[2,3,1]]) 
>>> m
$\displaystyle \left[\begin{matrix}1 & 2 & 3\\2 & 3 & 1\end{matrix}\right]$

Po wykonaniu powyższego polecenia w powłoce Pythona wygenerowane zostaną następujące dane wyjściowe -

[1 2 3 2 3 1]

Macierz jest tworzona z obiektów List o odpowiednim rozmiarze. Macierz można również uzyskać, rozdzielając elementy listy w określonej liczbie wierszy i kolumn.

>>> M=Matrix(2,3,[10,40,30,2,6,9]) 
>>> M
$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$

Po wykonaniu powyższego polecenia w powłoce Pythona wygenerowane zostaną następujące dane wyjściowe -

[10 40 30 2 6 9]

Matryca to obiekt zmienny. Moduł macierzy udostępnia również klasę ImmutableMatrix do uzyskiwania niezmiennej macierzy.

Podstawowa manipulacja

Plik shape właściwość obiektu Matrix zwraca jego rozmiar.

>>> M.shape

Dane wyjściowe dla powyższego kodu są następujące -

(2,3)

Metody row () i col () odpowiednio zwracają wiersz lub kolumnę o określonej liczbie.

>>> M.row(0)
$\displaystyle \left[\begin{matrix}10 & 40 & 30\end{matrix}\right]$

Dane wyjściowe dla powyższego kodu są następujące -

[10 40 30]

>>> M.col(1)
$\displaystyle \left[\begin{matrix}40\\6\end{matrix}\right]$

Dane wyjściowe dla powyższego kodu są następujące -

[40 6]

Użyj operatora plasterka Pythona, aby pobrać jeden lub więcej elementów należących do wiersza lub kolumny.

>>> M.row(1)[1:3]
[6, 9]

Klasa Matrix ma metody row_del () i col_del (), które usuwają określony wiersz / kolumnę z danej macierzy -

>>> M=Matrix(2,3,[10,40,30,2,6,9]) 
>>> M.col_del(1) 
>>> M

Po wykonaniu powyższego polecenia w powłoce Pythona wygenerowane zostaną następujące dane wyjściowe -

Matrix([[10, 30],[ 2, 9]])

Możesz zastosować styl do wyjścia za pomocą następującego polecenia -

$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$

Po wykonaniu powyższego fragmentu kodu otrzymasz następujące dane wyjściowe -

[10 30 2 9]

>>> M.row_del(0) 
>>> M

$\displaystyle \left[\begin{matrix}2 & 9\end{matrix}\right]$

Po wykonaniu powyższego fragmentu kodu otrzymasz następujące dane wyjściowe -

[2 9]

Podobnie metody row_insert () i col_insert () dodają wiersze lub kolumny o określonym indeksie wiersza lub kolumny

>>> M1=Matrix([[10,30]]) 
>>> M=M.row_insert(0,M1)
>>> M

$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$

Po wykonaniu powyższego fragmentu kodu otrzymasz następujące dane wyjściowe -

[10 40 30 2 9]

>>> M2=Matrix([40,6]) 
>>> M=M.col_insert(1,M2) 
>>> M

$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$

Po wykonaniu powyższego fragmentu kodu otrzymasz następujące dane wyjściowe -

[10 40 30 6 9]

Działania arytmetyczne

Zwykłe operatory +, - i * są zdefiniowane do wykonywania dodawania, odejmowania i mnożenia.

>>> M1=Matrix([[1,2,3],[3,2,1]]) 
>>> M2=Matrix([[4,5,6],[6,5,4]]) 
>>> M1+M2

$\displaystyle \left[\begin{matrix}5 & 7 & 9\\9 & 7 & 5\end{matrix}\right]$

Po wykonaniu powyższego fragmentu kodu otrzymasz następujące dane wyjściowe -

[5 7 9 9 7 5]

>>> M1-M2
$\displaystyle \left[\begin{matrix}-3 & -3 & -3\\-3 & -3 & -3\end{matrix}\right]$

Po wykonaniu powyższego fragmentu kodu otrzymasz następujące dane wyjściowe -

[- 3 -3 -3 -3 -3 -3]

Mnożenie macierzy jest możliwe tylko wtedy, gdy - Liczba kolumn pierwszej macierzy musi być równa liczbie wierszy drugiej macierzy. - Wynik będzie miał taką samą liczbę wierszy jak pierwsza macierz i taką samą liczbę kolumn jak druga macierz.

>>> M1=Matrix([[1,2,3],[3,2,1]]) 
>>> M2=Matrix([[4,5],[6,6],[5,4]]) 
>>> M1*M2
$\displaystyle \left[\begin{matrix}31 & 29\\29 & 31\end{matrix}\right]$

Dane wyjściowe dla powyższego kodu są następujące -

[31 29 29 31]

>>> M1.T
$\displaystyle \left[\begin{matrix}1 & 3\\2 & 2\\3 & 1\end{matrix}\right]$

Po wykonaniu kodu otrzymujemy następujące dane wyjściowe -

[1 3 2 2 3 1]

Aby obliczyć wyznacznik macierzy, użyj metody det (). Wyznacznik to wartość skalarna, którą można obliczyć z elementów macierzy kwadratowej. 0

>>> M=Matrix(3,3,[10,20,30,5,8,12,9,6,15])
>>> M
$\displaystyle \left[\begin{matrix}10 & 20 & 30\\5 & 8 & 12\\9 & 6 & 15\end{matrix}\right]$

Dane wyjściowe dla powyższego kodu są następujące -

[10 20 30 5 8 12 9 6 15]

>>> M.det()

Dane wyjściowe dla powyższego kodu są następujące -

-120

Konstruktorzy macierzy

SymPy udostępnia wiele specjalnych typów klas macierzy. Na przykład macierz tożsamości, macierz wszystkich zer i jedynek itp. Klasy te nazywane są odpowiednio jako oko, zera i jedynki. Macierz tożsamości to macierz kwadratowa, w której elementy leżące na przekątnej są ustawione na 1, pozostałe elementy mają wartość 0.

Example

from sympy.matrices import eye eye(3)

Output

Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])

$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]$

Dane wyjściowe dla powyższego kodu są następujące -

[1 0 0 0 1 0 0 0 1]

W macierzy diag elementy na przekątnej są inicjalizowane zgodnie z podanymi argumentami.

>>> from sympy.matrices import diag 
>>> diag(1,2,3)

$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 2 & 0\\0 & 0 & 3\end{matrix}\right]$

Dane wyjściowe dla powyższego kodu są następujące -

[1 0 0 0 2 0 0 0 3]

Wszystkie elementy w macierzy zer są inicjalizowane na 0.

>>> from sympy.matrices import zeros 
>>> zeros(2,3)

$\displaystyle \left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\end{matrix}\right]$

Dane wyjściowe dla powyższego kodu są następujące -

[0 0 0 0 0 0]

Podobnie, jedynki to macierz ze wszystkimi elementami ustawionymi na 1.

>>> from sympy.matrices import ones
>>> ones(2,3)

$\displaystyle \left[\begin{matrix}1 & 1 & 1\\1 & 1 & 1\end{matrix}\right]$

Dane wyjściowe dla powyższego kodu są następujące -

[1 1 1 1 1 1]

Pakiet Sympy ma klasę Function, która jest zdefiniowana w module sympy.core.function. Jest to klasa bazowa dla wszystkich stosowanych funkcji matematycznych, a także konstruktor dla niezdefiniowanych klas funkcji.

Następujące kategorie funkcji są dziedziczone z klasy funkcji -

Funkcje na liczbach zespolonych
Funkcje trygonometryczne
Funkcje dla liczby całkowitej
Funkcje kombinatoryczne
Inne różne funkcje

Funkcje na liczbach zespolonych

Ten zestaw funkcji jest zdefiniowany w sympy.functions.elementary.complexes moduł.

Ta funkcja zwraca rzeczywistą część wyrażenia -

>>> from sympy import * 
>>> re(5+3*I)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

>>> re(I)

Dane wyjściowe dla powyższego fragmentu kodu to -

Ta funkcja zwraca urojoną część wyrażenia -

>>> im(5+3*I)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

>>> im(I)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

sign

Ta funkcja zwraca złożony znak wyrażenia.

Dla prawdziwego wyrazu znak będzie -

1, jeśli wyrażenie jest pozytywne
0, jeśli wyrażenie jest równe zero
-1, jeśli wyrażenie jest ujemne

Jeśli wyrażenie jest urojone, zwracany znak to -

I jeśli im (wyrażenie) jest pozytywne
-I jeśli im (wyrażenie) jest ujemne

>>> sign(1.55), sign(-1), sign(S.Zero)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

(1, -1, 0)

>>> sign (-3*I), sign(I*2)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

(-I, I)

Abs

Ta funkcja zwraca wartość bezwzględną liczby zespolonej. Jest definiowana jako odległość między początkiem (0,0) a punktem (a, b) w płaszczyźnie zespolonej. Ta funkcja jest rozszerzeniem wbudowanej funkcji abs (), która akceptuje wartości symboliczne.

>>> Abs(2+3*I)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

$\sqrt13$

conjugate

Ta funkcja zwraca koniugat liczby zespolonej. Aby znaleźć sprzężenie złożone, zmieniamy znak części urojonej.

>>> conjugate(4+7*I)

Po wykonaniu powyższego fragmentu kodu otrzymasz następujące dane wyjściowe -

4 - 7i

Funkcje trygonometryczne

SymPy ma definicje wszystkich stosunków trygonometrycznych - sin cos, tan itp., A także ich odwrotne odpowiedniki, takie jak asin, acos, atan itp. Funkcje te obliczają odpowiednią wartość dla danego kąta wyrażoną w radianach.

>>> sin(pi/2), cos(pi/4), tan(pi/6)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

(1, sqrt(2)/2, sqrt(3)/3)

>>> asin(1), acos(sqrt(2)/2), atan(sqrt(3)/3)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

(pi/2, pi/4, pi/6)

Funkcje na liczbie całkowitej

Jest to zestaw funkcji do wykonywania różnych operacji na liczbie całkowitej.

ceiling

Jest to funkcja jednowymiarowa, która zwraca najmniejszą wartość całkowitą nie mniejszą niż jej argument. W przypadku liczb zespolonych, osobno sufit części rzeczywistej i urojonej.

>>> ceiling(pi), ceiling(Rational(20,3)), ceiling(2.6+3.3*I)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

(4, 7, 3 + 4*I)

floor

Ta funkcja zwraca największą wartość całkowitą nie większą niż jej argument. W przypadku liczb zespolonych ta funkcja również osobno obejmuje część rzeczywistą i urojoną.

>>> floor(pi), floor(Rational(100,6)), floor(6.3-5.9*I)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

(3, 16, 6 - 6*I)

frac

Ta funkcja reprezentuje ułamkową część x.

>>> frac(3.99), frac(Rational(10,3)), frac(10)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

(0.990000000000000, 1/3, 0)

Funkcje kombinatoryczne

Kombinatoryka to dziedzina matematyki zajmująca się problemami selekcji, uporządkowania i działania w systemie skończonym lub dyskretnym.

factorial

Silnia jest bardzo ważna w kombinatoryce, gdzie podaje liczbę sposobów permutacji n obiektów. Jest symbolicznie przedstawiony jako ð ?? '¥! Ta funkcja jest implementacją funkcji silni na nieujemnych liczbach całkowitych, silnia ujemnej liczby całkowitej to zespolona nieskończoność.

>>> x=Symbol('x') 
>>> factorial(x)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

>>> factorial(5)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

120

>>> factorial(-1)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

$\infty\backsim$

dwumianowy

Ta funkcja określa liczbę sposobów, w jakie możemy wybrać k elementów ze zbioru n elementów.

>>> x,y=symbols('x y') 
>>> binomial(x,y)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

$(\frac{x}{y})$

>>> binomial(4,2)

Dane wyjściowe dla powyższego fragmentu kodu są podane poniżej -

Rzędy trójkąta Pascala można generować za pomocą funkcji dwumianowej.

>>> for i in range(5): print ([binomial(i,j) for j in range(i+1)])

Po wykonaniu powyższego fragmentu kodu otrzymasz następujące dane wyjściowe -

[1]

[1, 1]

[1, 2, 1]

[1, 3, 3, 1]

[1, 4, 6, 4, 1]

fibonacci

Liczby Fibonacciego to sekwencja liczb całkowitych określona przez początkowe wyrażenia F0 = 0, F1 = 1 i dwustopniowa relacja powtarzania Fn = Fnâˆ'1 + Fnâˆ'2.

>>> [fibonacci(x) for x in range(10)]

Poniższe dane wyjściowe są uzyskiwane po wykonaniu powyższego fragmentu kodu -

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

tribonacci

Liczby Tribonacciego to sekwencja liczb całkowitych zdefiniowana przez początkowe wyrażenia F0 = 0, F1 = 1, F2 = 1 i trzyokresowa relacja powtarzania Fn = Fn-1 + Fn-2 + Fn-3.

>>> tribonacci(5, Symbol('x'))

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x^8 + 3x^5 + 3x^2$

>>> [tribonacci(x) for x in range(10)]

Poniższe dane wyjściowe są uzyskiwane po wykonaniu powyższego fragmentu kodu -

[0, 1, 1, 2, 4, 7, 13, 24, 44, 81]

Różne funkcje

Poniżej znajduje się lista niektórych często używanych funkcji -

Min- Zwraca minimalną wartość listy. Nazywa się Min, aby uniknąć konfliktów z wbudowaną funkcją min.

Max- Zwraca maksymalną wartość listy. Nazywa się Max, aby uniknąć konfliktów z wbudowaną funkcją max.

root - Zwraca n-ty pierwiastek z x.

sqrt - Zwraca główny pierwiastek kwadratowy z x.

cbrt - Ta funkcja oblicza główny pierwiastek sześcienny z x, (skrót do x ++ Rational (1,3)).

Poniżej znajdują się przykłady powyższych funkcji dodatkowych i ich odpowiednich wyjść -

>>> Min(pi,E)

>>> Max(5, Rational(11,2))

$\frac{11}{2}$

>>> root(7,Rational(1,2))

>>> sqrt(2)

$\sqrt2$

>>> cbrt(1000)

W matematyce system liczb Quaternion jest rozszerzeniem liczb zespolonych. Każdy obiekt Quaternion zawiera cztery zmienne skalarne i cztery wymiary, jeden wymiar rzeczywisty i trzy wymiary urojone.

Quaternion jest reprezentowany przez następujące wyrażenie -

q = a + bi + cj + dk

gdzie a, b, c id są liczbami rzeczywistymi i i, j, k są jednostkami kwaternionów takimi, że i2 == j2 == k2 == ijk

Plik sympy.algebras.quaternion moduł ma klasę Quaternion.

>>> from sympy.algebras.quaternion import Quaternion 
>>> q=Quaternion(2,3,1,4) 
>>> q

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$2 + 3i + 1j + 4k$

Quaternions są używane w czystej matematyce, a także w matematyce stosowanej, grafice komputerowej, wizji komputerowej itp.

>>> from sympy import * 
>>> x=Symbol('x') 
>>> q1=Quaternion(x**2, x**3, x) >>> q1

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$x^2 + x^3i + xj + 0k$

Obiekt Quaternion może również mieć wyimaginowane współczynniki

>>> q2=Quaternion(2,(3+2*I), x**2, 3.5*I) 
>>> q2

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$2 + (3 + 2i)i + x2j + 3.5ik$

Dodaj()

Ta metoda dostępna w klasie Quaternion umożliwia dodanie dwóch obiektów Quaternion.

>>> q1=Quaternion(1,2,3,4) 
>>> q2=Quaternion(4,3,2,1) 
>>> q1.add(q2)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$5 + 5i + 5j + 5k$

W obiekcie Quaternion można dodać liczbę lub symbol.

>>> q1+2

Poniższe dane wyjściowe są uzyskiwane po wykonaniu powyższego fragmentu kodu -

$3 + 2i + 3j + 4k$

>>> q1+x

Poniższe dane wyjściowe są uzyskiwane po wykonaniu powyższego fragmentu kodu -

$(x + 1) + 2i + 3j + 4k$

mul ()

Ta metoda wykonuje mnożenie dwóch obiektów kwaternionów.

>>> q1=Quaternion(1,2,1,2) 
>>> q2=Quaternion(2,4,3,1) 
>>> q1.mul(q2)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$(-11) + 3i + 11j + 7k$

odwrotność()

Ta metoda zwraca odwrotność obiektu quaternion.

>>> q1.inverse()

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{1}{10} + (-\frac{1}{5})i + (-\frac{1}{10})j + (-\frac{1}{5})k$

pow ()

Ta metoda zwraca moc obiektu quaternion.

>>> q1.pow(2)

Poniższe dane wyjściowe są uzyskiwane po wykonaniu powyższego fragmentu kodu -

$(-8) + 4i + 2j + 4k$

exp ()

Ta metoda oblicza wykładniczy obiekt Quaternion, tj. Eq

>>> q=Quaternion(1,2,4,3) 
>>> q.exp()

Poniższe dane wyjściowe są uzyskiwane po wykonaniu powyższego fragmentu kodu -

$e\cos(\sqrt29) + \frac{2\sqrt29e\sin(\sqrt29)}{29}i + \frac{4\sqrt29e\sin(\sqrt29)}{29}j + \frac{3\sqrt29e\sin}{29}k$

Ponieważ symbole = i == są zdefiniowane jako operatory przypisania i równości w Pythonie, nie można ich używać do formułowania równań symbolicznych. SymPy udostępnia funkcję Eq () do tworzenia równania.

>>> from sympy import * 
>>> x,y=symbols('x y') 
>>> Eq(x,y)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

x = y

Ponieważ x = y jest możliwe wtedy i tylko wtedy, gdy xy = 0, powyższe równanie można zapisać jako -

>>> Eq(x-y,0)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

x − y = 0

Moduł solvera w SymPy udostępnia funkcję soveset (), której prototyp wygląda następująco -

solveset(equation, variable, domain)

Domena to domyślnie S.Complexes. Korzystając z funkcji solveset (), możemy rozwiązać równanie algebraiczne w następujący sposób -

>>> solveset(Eq(x**2-9,0), x)

Uzyskuje się następujący wynik -

{−3, 3}

>>> solveset(Eq(x**2-3*x, -2),x)

Poniższe dane wyjściowe są uzyskiwane po wykonaniu powyższego fragmentu kodu -

{1,2}

Dane wyjściowe zestawu solveset to zestaw skończony rozwiązań. Jeśli nie ma rozwiązań, zwracany jest EmptySet

>>> solveset(exp(x),x)

Poniższe dane wyjściowe są uzyskiwane po wykonaniu powyższego fragmentu kodu -

$\varnothing$

Równanie liniowe

Aby rozwiązać równania liniowe, musimy użyć funkcji linsolve ().

Na przykład równania są następujące -

xy = 4

x + y = 1

>>> from sympy import * 
>>> x,y=symbols('x y') 
>>> linsolve([Eq(x-y,4),Eq( x + y ,1) ], (x, y))

Poniższe dane wyjściowe są uzyskiwane po wykonaniu powyższego fragmentu kodu -

$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$

Funkcja linsolve () może również rozwiązywać równania liniowe wyrażone w postaci macierzy.

>>> a,b=symbols('a b') 
>>> a=Matrix([[1,-1],[1,1]]) 
>>> b=Matrix([4,1]) 
>>> linsolve([a,b], (x,y))

Otrzymamy następujące dane wyjściowe, jeśli wykonamy powyższy fragment kodu -

$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$

Równanie nieliniowe

W tym celu używamy funkcji nonlinsolve (). Równania dla tego przykładu -

a ² + a = 0 ab = 0

>>> a,b=symbols('a b') 
>>> nonlinsolve([a**2 + a, a - b], [a, b])

Otrzymamy następujące dane wyjściowe, jeśli wykonamy powyższy fragment kodu -

$\lbrace(-1, -1),(0,0)\rbrace$

równanie różniczkowe

Najpierw utwórz niezdefiniowaną funkcję, przekazując cls = Function do funkcji symbols. Aby rozwiązać równania różniczkowe, użyj funkcji dsolve.

>>> x=Symbol('x') 
>>> f=symbols('f', cls=Function) 
>>> f(x)

Poniższe dane wyjściowe są uzyskiwane po wykonaniu powyższego fragmentu kodu -

f(x)

Tutaj f (x) jest niedocenianą funkcją. Jego pochodna jest następująca -

>>> f(x).diff(x)

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$\frac{d}{dx}f(x)$

Najpierw tworzymy obiekt Eq odpowiadający następującemu równaniu różniczkowemu

>>> eqn=Eq(f(x).diff(x)-f(x), sin(x)) 
>>> eqn

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$-f(x) + \frac{d}{dx}f(x)= \sin(x)$

>>> dsolve(eqn, f(x))

Powyższy fragment kodu daje wynik odpowiadający poniższemu wyrażeniu -

$f(x)=(c^1-\frac{e^-xsin(x)}{2}-\frac{e^-xcos(x)}{2})e^x$

SymPy używa biblioteki Matplotlib jako zaplecza do renderowania dwuwymiarowych i trójwymiarowych wykresów funkcji matematycznych. Upewnij się, że Matplotlib jest dostępny w bieżącej instalacji Pythona. Jeśli nie, zainstaluj to samo za pomocą następującego polecenia -

pip install matplotlib

Obsługa drukowania jest zdefiniowana w module sympy.plotting. W module kreślącym dostępne są następujące funkcje -

plot - wykresy liniowe 2D
plot3d - wykresy liniowe 3D
plot_parametric - wykresy parametryczne 2D
plot3d_parametric - wykresy parametryczne 3D

Funkcja plot () zwraca instancję klasy Plot. Rysunek wykresu może mieć jedno lub więcej wyrażeń SymPy. Chociaż może używać Matplotlib jako zaplecza, można również używać innych backendów, takich jak texplot, pyglet lub Google charts API.

plot(expr, range, kwargs)

gdzie wyrażenie jest dowolnym prawidłowym wyrażeniem symPy. Jeśli nie wspomniano, zakres używa wartości domyślnej (-10, 10).

Poniższy przykład przedstawia wartości x2 dla każdej wartości w zakresie (-10,10) -

>>> from sympy.plotting import plot 
>>> from sympy import * 
>>> x=Symbol('x') 
>>> plot(x**2, line_color='red')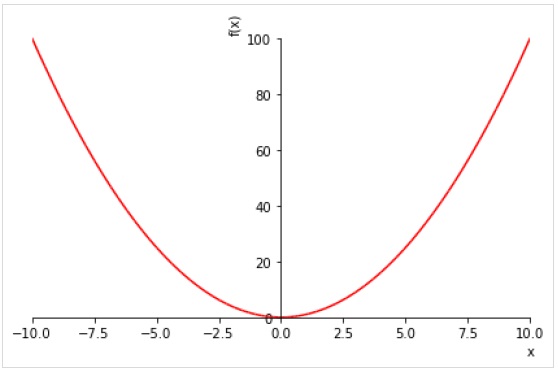

Aby narysować wiele wykresów dla tego samego zakresu, podaj wiele wyrażeń przed krotką zakresu.

>>> plot( sin(x),cos(x), (x, -pi, pi))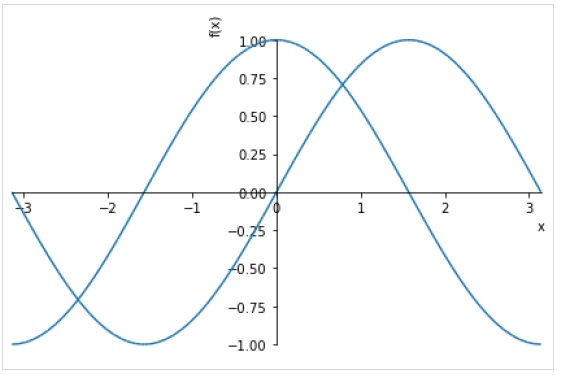

Możesz również określić oddzielny zakres dla każdego wyrażenia.

plot((expr1, range1), (expr2, range2))

Poniższy rysunek przedstawia sin (x) i cos (x) w różnych zakresach.

>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)))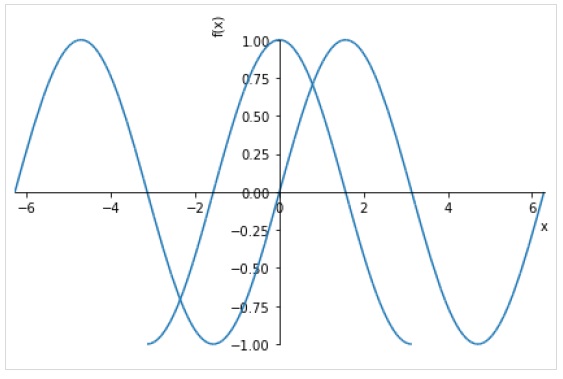

W funkcji plot () można podać następujące opcjonalne argumenty słów kluczowych.

line_color - określa kolor linii działki.
title - ciąg znaków do wyświetlenia jako tytuł
xlabel - ciąg do wyświetlenia jako etykieta dla osi X.
ylabel - ciąg do wyświetlenia jako etykieta dla osi y

>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)), line_color='red', title='SymPy plot example')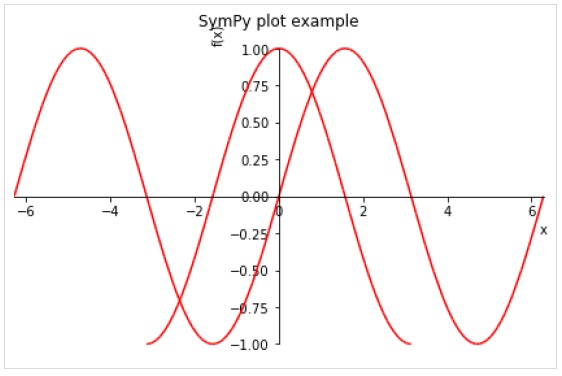

Funkcja plot3d () renderuje trójwymiarowy wykres.

plot3d(expr, xrange, yrange, kwargs)

Poniższy przykład rysuje wykres powierzchni 3D -

>>> from sympy.plotting import plot3d 
>>> x,y=symbols('x y') 
>>> plot3d(x*y, (x, -10,10), (y, -10,10))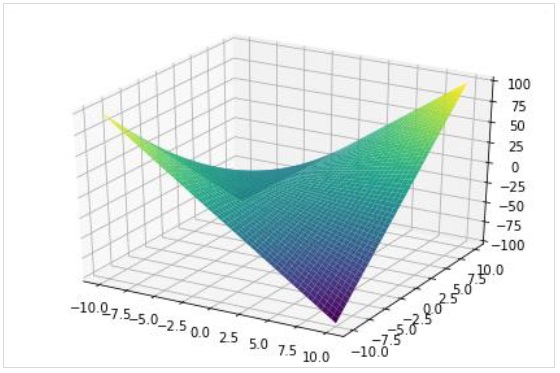

Podobnie jak w przypadku wykresu 2D, wykres trójwymiarowy może mieć wiele wykresów, z których każdy ma inny zakres.

>>> plot3d(x*y, x/y, (x, -5, 5), (y, -5, 5))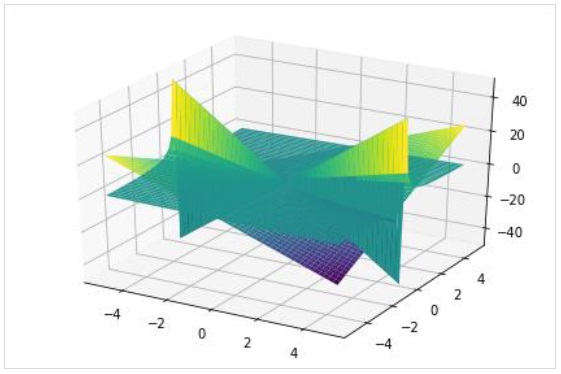

Funkcja plot3d_parametric_line () renderuje trójwymiarowy parametryczny wykres liniowy.

>>> from sympy.plotting import plot3d_parametric_line 
>>> plot3d_parametric_line(cos(x), sin(x), x, (x, -5, 5))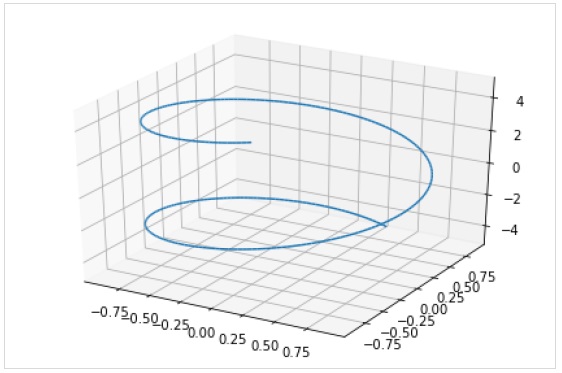

Aby narysować parametryczny wykres powierzchni, użyj funkcji plot3d_parametric_surface ().

plot3d_parametric_surface(xexpr, yexpr, zexpr, rangex, rangey, kwargs)

>>> from sympy.plotting import plot3d_parametric_surface 
>>> plot3d_parametric_surface(cos(x+y), sin(x-y), x-y, (x, -5, 5), (y, -5, 5))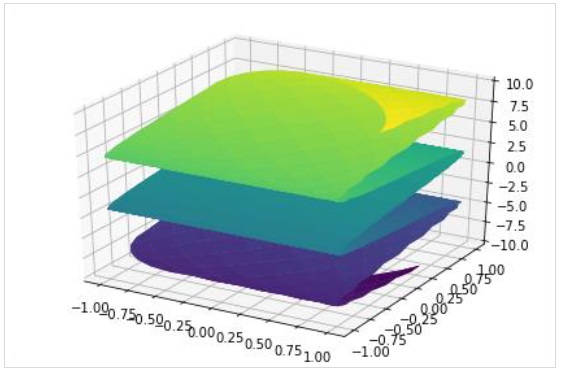

Moduł geometrii w SymPy pozwala na tworzenie dwuwymiarowych obiektów, takich jak linia, okrąg itp. Możemy wtedy uzyskać o nich informacje, takie jak sprawdzenie współliniowości czy znalezienie przecięcia.

Punkt

Klasa Point reprezentuje punkt w przestrzeni euklidesowej. Poniższy przykład sprawdza kolinearność punktów -

>>> from sympy.geometry import Point 
>>> from sympy import * 
>>> x=Point(0,0) 
>>> y=Point(2,2) 
>>> z=Point(4,4) 
>>> Point.is_collinear(x,y,z)

Output

True

>>> a=Point(2,3) 
>>> Point.is_collinear(x,y,a)

Output

False

Metoda distance () klasy Point oblicza odległość między dwoma punktami

>>> x.distance(y)

Output

$2\sqrt2$

Odległość można również przedstawić za pomocą symboli.

Linia

Element linii jest uzyskiwany z dwóch obiektów Point. Metoda intersection () zwraca punkt przecięcia, jeśli dwie linie się przecinają.

>>> from sympy.geometry import Point, Line 
>>> p1, p2=Point(0,5), Point(5,0) 
>>> l1=Line(p1,p2)
>>> l2=Line(Point(0,0), Point(5,5)) 
>>> l1.intersection(l2)

Output

[Point2D(5/2, 5/2)]

>>> l1.intersection(Line(Point(0,0), Point(2,2)))

Output

[Point2D(5/2, 5/2)]

>>> x,y=symbols('x y') 
>>> p=Point(x,y) 
>>> p.distance(Point(0,0))

Output

$\sqrt{x^2 + y^2}$

Trójkąt

Ta funkcja buduje trójkąt z trzech obiektów punktowych.

Triangle(a,b,c)

>>> t=Triangle(Point(0,0),Point(0,5), Point(5,0)) 
>>> t.area

Output

$-\frac{25}{2}$

Elipsa

Element geometrii eliptycznej jest konstruowany przez przekazanie obiektu Point odpowiadającego środkowi i po dwie liczby określające promień poziomy i pionowy.

ellipse(center, hradius, vradius)

>>> from sympy.geometry import Ellipse, Line 
>>> e=Ellipse(Point(0,0),8,3) 
>>> e.area

Output

$24\pi$

Promień vradius można uzyskać pośrednio za pomocą parametru mimośrodowości.

>>> e1=Ellipse(Point(2,2), hradius=5, eccentricity=Rational(3,4)) 
>>> e1.vradius

Output

$\frac{5\sqrt7}{4}$

Plik apoapsis elipsy to największa odległość między ogniskiem a konturem.

>>> e1.apoapsis

Output

$\frac{35}{4}$

Poniższa instrukcja oblicza obwód elipsy -

>>> e1.circumference

Output

$20E(\frac{9}{16})$

Plik equation metoda elipsy zwraca równanie elipsy.

>>> e1.equation(x,y)

Output

$(\frac{x}{5}-\frac{2}{5})^2 + \frac{16(y-2)2}{175} - 1$

W matematyce zbiór to dobrze zdefiniowany zbiór odrębnych obiektów, którymi mogą być liczby, ludzie, litery alfabetu lub nawet inne zbiory. Set jest również jednym z typów wbudowanych w Pythonie. SymPy udostępnia moduł zestawów. Zawiera definicje różnych typów zestawów i ma funkcje do wykonywania operacji na zbiorach, takich jak przecięcie, suma itp.

Zestaw jest klasą bazową dla dowolnego innego typu zestawu w SymPy. Zauważ, że różni się on od wbudowanego zestawu danych typu Python. Klasa Interval reprezentuje rzeczywiste interwały, a jej właściwość boundary zwraca aFiniteSet obiekt.

>>> from sympy import Interval 
>>> s=Interval(1,10).boundary 
>>> type(s)

sympy.sets.sets.FiniteSet

FiniteSet to zbiór liczb dyskretnych. Można go uzyskać z dowolnego obiektu sekwencji, takiego jak lista lub łańcuch.

>>> from sympy import FiniteSet 
>>> FiniteSet(range(5))

Output

$\lbrace\lbrace0,1,...,4\rbrace\rbrace$

>>> numbers=[1,3,5,2,8] 
>>> FiniteSet(*numbers)

Output

$\lbrace1,2,3,5,8\rbrace$

>>> s="HelloWorld" 
>>> FiniteSet(*s)

Output

{H,W,d,e,l,o,r}

Zwróć uwagę, że podobnie jak w zestawie wbudowanym, SymPy's Set jest również zbiorem odrębnych obiektów.

ConditionSet to zbiór elementów spełniających określony warunek

>>> from sympy import ConditionSet, Eq, Symbol 
>>> x=Symbol('x') 
>>> s=ConditionSet(x, Eq(x**2-2*x,0), Interval(1,10)) >>> s

Output

$\lbrace x\mid x\in[1,10]∧x^2 - 2x =0\rbrace$

Unionjest zbiorem złożonym. Zawiera wszystkie elementy w dwóch zestawach. Zwróć uwagę, że elementy, które znajdują się w obu, pojawią się tylko raz w Unii.

>>> from sympy import Union 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> Union(a,b)

Intersection z drugiej strony zawiera tylko te elementy, które są obecne w obu.

>>> from sympy import Intersection 
>>> Intersection(a,b)

ProductSet obiekt reprezentuje iloczyn kartezjański elementów w obu zbiorach.

>>> from sympy import ProductSet 
>>> l1=[1,2] 
>>> l2=[2,3] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> set(ProductSet(a,b))

Complement(a,b) zachowuje elementy z elementów wykluczających, które są wspólne z zestawem b.

>>> from sympy import Complement 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> Complement(a,b), Complement(b,a)

SymmetricDifference zestaw zawiera tylko nietypowe elementy w obu zestawach.

>>> from sympy import SymmetricDifference 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> SymmetricDifference(a,b)

Output

{2,3,5,9}

W SymPy dostępnych jest kilka drukarek. Poniżej znajduje się częściowa lista -

str
srepr
Ładna drukarka ASCII
Ładna drukarka Unicode
LaTeX
MathML
Dot

Obiekty SymPy mogą być również wysyłane jako dane wyjściowe do kodu różnych języków, takich jak C, Fortran, Javascript, Theano i Python.

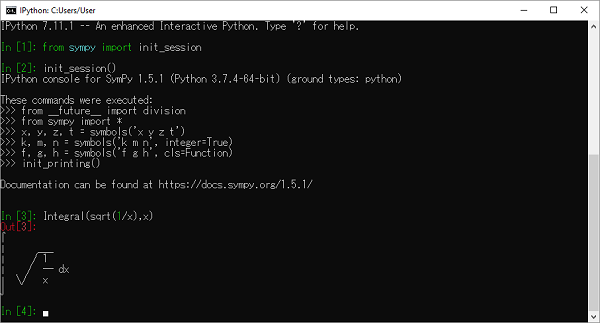
SymPy używa znaków Unicode do renderowania danych wyjściowych w postaci ładnego wydruku. Jeśli używasz konsoli Pythona do wykonywania sesji SymPy, najlepsze ładne środowisko drukowania jest aktywowane przez wywołanie funkcji init_session ().

>>> from sympy import init_session 
>>> init_session()

Konsola IPython dla SymPy 1.5.1 (Python 3.7.4-64-bit) (typy naziemne: python).

Te polecenia zostały wykonane -

>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()

Dokumentację można znaleźć pod adresem https://docs.sympy.org/1.5.1/.

>>> Integral(sqrt(1/x),x)

$\int \sqrt\frac{1}{x} dx$

Jeśli LATEX nie jest zainstalowany, ale jest zainstalowany Matplotlib, użyje silnika renderującego Matplotlib. Jeśli Matplotlib nie jest zainstalowany, używa ładnej drukarki Unicode. Jednak notatnik Jupyter używa MathJax do renderowania LATEX-a.

W terminalu, który nie obsługuje Unicode, używana jest ładna drukarka ASCII.

Aby użyć drukarki ASCII, użyj funkcji pprint () z właściwością use_unicode ustawioną na False

>>> pprint(Integral(sqrt(1/x),x),use_unicode=False)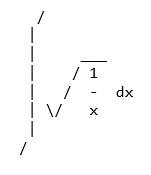

Dostęp do drukarki pretty Unicode można również uzyskać z pprint () i pretty (). Jeśli terminal obsługuje Unicode, jest używany automatycznie. Jeśli pprint () nie jest w stanie wykryć, że terminal obsługuje Unicode, możesz przekazać use_unicode = True, aby zmusić go do używania Unicode.

Aby otrzymać wyrażenie LATEX, użyj funkcji latex ().

>>> print(latex(Integral(sqrt(1/x),x)))

\int \sqrt{\frac{1}{x}}\, dx

Możesz także użyć drukarki mathml. w tym celu zaimportuj funkcję print_mathml. Wersja tekstowa jest uzyskiwana przez funkcję mathml ().

>>> from sympy.printing.mathml import print_mathml 
>>> print_mathml(Integral(sqrt(1/x),x))

<apply>

<int/>

<bvar>

<ci>x</ci>

</bvar>

<apply>

<root/>

<apply>

<power/>

<ci>x</ci>

<cn>-1</cn>

</apply>

>>>mathml(Integral(sqrt(1/x),x))

'<apply><int/><bvar><ci>x</ci></bvar><apply><root/><apply><power/><ci>x</ci><cn>-1</cn></apply></apply></apply>'