Análise de Big Data - Tabelas e gráficos

A primeira abordagem para analisar dados é analisá-los visualmente. Os objetivos de fazer isso normalmente são encontrar relações entre variáveis e descrições univariadas das variáveis. Podemos dividir essas estratégias como -

Análise univariada
Análise multivariada

Métodos Gráficos Univariados

Univariateé um termo estatístico. Na prática, significa que queremos analisar uma variável independentemente do resto dos dados. Os gráficos que permitem fazer isso de forma eficiente são -

Box-Plots

Box-Plots são normalmente usados para comparar distribuições. É uma ótima maneira de inspecionar visualmente se há diferenças entre as distribuições. Podemos ver se existem diferenças entre o preço dos diamantes para cortes diferentes.

# We will be using the ggplot2 library for plotting
library(ggplot2)  
data("diamonds")  

# We will be using the diamonds dataset to analyze distributions of numeric variables 
head(diamonds) 

#    carat   cut       color  clarity  depth  table   price    x     y     z 
# 1  0.23    Ideal       E      SI2    61.5    55     326     3.95  3.98  2.43 
# 2  0.21    Premium     E      SI1    59.8    61     326     3.89  3.84  2.31 
# 3  0.23    Good        E      VS1    56.9    65     327     4.05  4.07  2.31 
# 4  0.29    Premium     I      VS2    62.4    58     334     4.20  4.23  2.63 
# 5  0.31    Good        J      SI2    63.3    58     335     4.34  4.35  2.75 
# 6  0.24    Very Good   J      VVS2   62.8    57     336     3.94  3.96  2.48 

### Box-Plots
p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) + 
   geom_box-plot() + 
   theme_bw() 
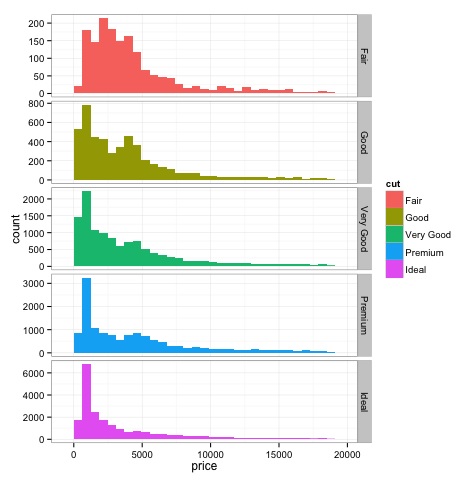
print(p)

Podemos observar no gráfico que existem diferenças na distribuição do preço dos diamantes nos diferentes tipos de corte.

Histogramas

source('01_box_plots.R')

# We can plot histograms for each level of the cut factor variable using 
facet_grid 
p = ggplot(diamonds, aes(x = price, fill = cut)) + 
   geom_histogram() + 
   facet_grid(cut ~ .) + 
   theme_bw() 

p  
# the previous plot doesn’t allow to visuallize correctly the data because of 
the differences in scale 
# we can turn this off using the scales argument of facet_grid  

p = ggplot(diamonds, aes(x = price, fill = cut)) + 
   geom_histogram() + 
   facet_grid(cut ~ ., scales = 'free') + 
   theme_bw() 
p  

png('02_histogram_diamonds_cut.png') 
print(p) 
dev.off()

A saída do código acima será a seguinte -

Métodos gráficos multivariados

Métodos gráficos multivariados na análise exploratória de dados têm o objetivo de encontrar relações entre diferentes variáveis. Existem duas maneiras de fazer isso que são comumente usadas: traçar uma matriz de correlação de variáveis numéricas ou simplesmente traçar os dados brutos como uma matriz de gráficos de dispersão.

Para demonstrar isso, usaremos o conjunto de dados de diamantes. Para seguir o código, abra o scriptbda/part2/charts/03_multivariate_analysis.R.

library(ggplot2)
data(diamonds) 

# Correlation matrix plots  
keep_vars = c('carat', 'depth', 'price', 'table') 
df = diamonds[, keep_vars]  
# compute the correlation matrix 
M_cor = cor(df) 

#          carat       depth      price      table 
# carat 1.00000000  0.02822431  0.9215913  0.1816175 
# depth 0.02822431  1.00000000 -0.0106474 -0.2957785 
# price 0.92159130 -0.01064740  1.0000000  0.1271339 
# table 0.18161755 -0.29577852  0.1271339  1.0000000  

# plots 
heat-map(M_cor)

O código produzirá a seguinte saída -

Este é um resumo, nos diz que existe uma forte correlação entre o preço e o acento circunflexo, e não muito entre as outras variáveis.

Uma matriz de correlação pode ser útil quando temos um grande número de variáveis, caso em que traçar os dados brutos não seria prático. Como mencionado, é possível mostrar os dados brutos também -

library(GGally)
ggpairs(df)

Podemos ver no gráfico que os resultados exibidos no mapa de calor são confirmados, há uma correlação de 0,922 entre as variáveis de preço e quilate.

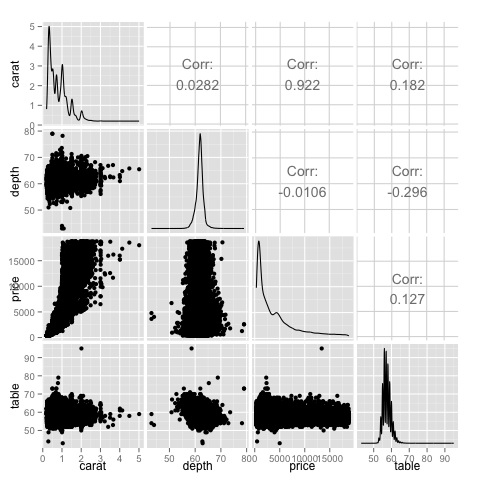
É possível visualizar essa relação no gráfico de dispersão preço-quilate localizado no índice (3, 1) da matriz do gráfico de dispersão.