Análise de Big Data - Análise de série temporal
A série temporal é uma sequência de observações de variáveis categóricas ou numéricas indexadas por uma data ou registro de data e hora. Um exemplo claro de dados de série temporal é a série temporal do preço de uma ação. Na tabela a seguir, podemos ver a estrutura básica dos dados da série temporal. Neste caso, as observações são registradas a cada hora.
| Timestamp | Estoque - Preço |
|---|---|
| 11/10/2015 09:00:00 | 100 |
| 11/10/2015 10:00:00 | 110 |
| 11/10/2015 11:00:00 | 105 |
| 11/10/2015 12:00:00 | 90 |
| 11/10/2015 13:00:00 | 120 |
Normalmente, a primeira etapa na análise de série temporal é plotar a série; isso normalmente é feito com um gráfico de linha.
A aplicação mais comum da análise de série temporal é prever valores futuros de um valor numérico usando a estrutura temporal dos dados. Isso significa que as observações disponíveis são usadas para prever valores do futuro.
A ordenação temporal dos dados implica que os métodos tradicionais de regressão não são úteis. Para construir uma previsão robusta, precisamos de modelos que levem em consideração a ordenação temporal dos dados.
O modelo mais usado para Análise de Séries Temporais é chamado Autoregressive Moving Average(ARMA). O modelo consiste em duas partes, umautoregressive (AR) parte e um moving average(MA) parte. O modelo é geralmente referido como modelo ARMA (p, q) , onde p é a ordem da parte autorregressiva eq é a ordem da parte média móvel.
Modelo Autoregressivo
O AR (p) é lido como um modelo autoregressivo de ordem p. Matematicamente, é escrito como -
$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$
onde {φ 1 ,…, φ p } são parâmetros a serem estimados, c é uma constante e a variável aleatória ε t representa o ruído branco. Algumas restrições são necessárias nos valores dos parâmetros para que o modelo permaneça estacionário.
Média Móvel
A notação MA (q) refere-se ao modelo de média móvel de ordem q -
$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$
onde θ 1 , ..., θ q são os parâmetros do modelo, μ é a expectativa de X t , e ε t , ε t - 1 , ... são, termos de erro de ruído branco.
Média Móvel Autoregressiva
O modelo ARMA (p, q) combina p termos autorregressivos e q termos de média móvel. Matematicamente, o modelo é expresso com a seguinte fórmula -
$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varejpsilon_ {ti} $$
Podemos ver que o modelo ARMA (p, q) é uma combinação dos modelos AR (p) e MA (q) .
Para dar alguma intuição do modelo, considere que a parte AR da equação busca estimar parâmetros para X t - i observações de a fim de prever o valor da variável em X t . É no final uma média ponderada dos valores anteriores. A seção MA usa a mesma abordagem, mas com o erro das observações anteriores, ε t - i . Portanto, no final, o resultado do modelo é uma média ponderada.
O seguinte trecho de código demonstra como implementar uma ARMA (p, q) em R .
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)Traçar os dados normalmente é a primeira etapa para descobrir se há uma estrutura temporal nos dados. Podemos ver no gráfico que há fortes picos no final de cada ano.
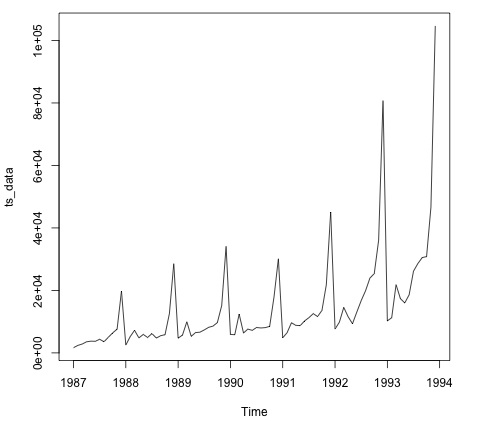
O código a seguir ajusta um modelo ARMA aos dados. Executa várias combinações de modelos e seleciona aquele que apresenta menos erro.
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172