Análise de Big Data - Métodos Estatísticos

Ao analisar os dados, é possível ter uma abordagem estatística. As ferramentas básicas necessárias para realizar a análise básica são -

• Análise de correlação
• Análise de variação
• Testando hipóteses

Ao trabalhar com grandes conjuntos de dados, isso não envolve um problema, pois esses métodos não são computacionalmente intensivos, com exceção da análise de correlação. Nesse caso, sempre é possível tirar uma amostra e os resultados devem ser robustos.

Análise de correlação

A Análise de Correlação procura encontrar relações lineares entre variáveis ​​numéricas. Isso pode ser útil em diferentes circunstâncias. Um uso comum é a análise exploratória de dados, na seção 16.0.2 do livro há um exemplo básico dessa abordagem. Em primeiro lugar, a métrica de correlação usada no exemplo mencionado é baseada naPearson coefficient. No entanto, há outra métrica interessante de correlação que não é afetada por outliers. Essa métrica é chamada de correlação spearman.

o spearman correlation métrica é mais robusta à presença de outliers do que o método de Pearson e fornece melhores estimativas das relações lineares entre as variáveis ​​numéricas quando os dados não são normalmente distribuídos.

library(ggplot2)

# Select variables that are interesting to compare pearson and spearman 
correlation methods. 
x = diamonds[, c('x', 'y', 'z', 'price')]  

# From the histograms we can expect differences in the correlations of both 
metrics.  
# In this case as the variables are clearly not normally distributed, the 
spearman correlation 

# is a better estimate of the linear relation among numeric variables. 
par(mfrow = c(2,2)) 
colnm = names(x) 
for(i in 1:4) { 
   hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i])) 
} 
par(mfrow = c(1,1))

A partir dos histogramas da figura a seguir, podemos esperar diferenças nas correlações de ambas as métricas. Nesse caso, como as variáveis ​​claramente não têm distribuição normal, a correlação de Spearman é uma estimativa melhor da relação linear entre as variáveis ​​numéricas.

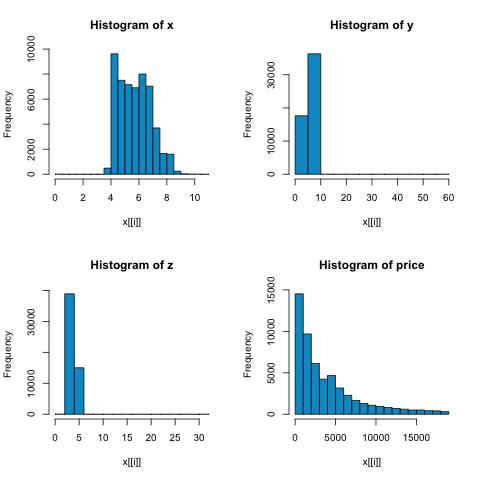
Para calcular a correlação em R, abra o arquivo bda/part2/statistical_methods/correlation/correlation.R que tem esta seção de código.

## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson') 
cor_spearman <- cor(x, method = 'spearman')  

### Pearson Correlation 
print(cor_pearson) 
#            x          y          z        price 
# x      1.0000000  0.9747015  0.9707718  0.8844352 
# y      0.9747015  1.0000000  0.9520057  0.8654209 
# z      0.9707718  0.9520057  1.0000000  0.8612494 
# price  0.8844352  0.8654209  0.8612494  1.0000000  

### Spearman Correlation 
print(cor_spearman) 
#              x          y          z      price 
# x      1.0000000  0.9978949  0.9873553  0.9631961 
# y      0.9978949  1.0000000  0.9870675  0.9627188 
# z      0.9873553  0.9870675  1.0000000  0.9572323 
# price  0.9631961  0.9627188  0.9572323  1.0000000

Teste Qui-quadrado

O teste qui-quadrado nos permite testar se duas variáveis ​​aleatórias são independentes. Isso significa que a distribuição de probabilidade de cada variável não influencia a outra. Para avaliar o teste em R, precisamos primeiro criar uma tabela de contingência e, em seguida, passá-la para ochisq.test R função.

Por exemplo, vamos verificar se existe uma associação entre as variáveis: corte e cor do conjunto de dados de diamantes. O teste é formalmente definido como -

• H0: O corte variável e o diamante são independentes
• H1: O corte variável e o diamante não são independentes

Suporíamos que existe uma relação entre essas duas variáveis ​​por seus nomes, mas o teste pode fornecer uma "regra" objetiva dizendo o quão significativo é esse resultado ou não.

No fragmento de código a seguir, descobrimos que o valor p do teste é 2,2e-16, isso é quase zero em termos práticos. Então, depois de executar o teste, fazer umMonte Carlo simulation, descobrimos que o valor p é 0,0004998, que ainda é bastante inferior ao limite 0,05. Este resultado significa que rejeitamos a hipótese nula (H0), então acreditamos nas variáveiscut e color não são independentes.

library(ggplot2)

# Use the table function to compute the contingency table 
tbl = table(diamonds$cut, diamonds$color) 
tbl  

#              D    E    F    G    H    I    J 
# Fair       163  224  312  314  303  175  119 
# Good       662  933  909  871  702  522  307 
# Very Good 1513 2400 2164 2299 1824 1204  678 
# Premium   1603 2337 2331 2924 2360 1428  808 
# Ideal     2834 3903 3826 4884 3115 2093  896  

# In order to run the test we just use the chisq.test function. 
chisq.test(tbl)  

# Pearson’s Chi-squared test 
# data:  tbl 
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation 
# It's needed to add the simulate.p.value = TRUE flag and the amount of 
simulations 
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)  

# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates) 
# data:  tbl 
# X-squared = 310.32, df = NA, p-value = 0.0004998

Teste t

A ideia de t-testé avaliar se existem diferenças na distribuição de uma variável numérica # entre diferentes grupos de uma variável nominal. Para demonstrar isso, selecionarei os níveis dos níveis Justo e Ideal do fator de corte variável, em seguida, compararemos os valores de uma variável numérica entre esses dois grupos.

data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]

data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the 
cut variable 
df1 = data[, c('cut', 'price')]  

# We can see the price means are different for each group 
tapply(df1$price, df1$cut, mean) 
# Fair    Ideal  
# 4358.758 3457.542

Os testes t são implementados em R com o t.testfunção. A interface da fórmula para t.test é a maneira mais simples de usá-la, a ideia é que uma variável numérica é explicada por uma variável de grupo.

Por exemplo: t.test(numeric_variable ~ group_variable, data = data). No exemplo anterior, onumeric_variable é price e a group_variable é cut.

Do ponto de vista estatístico, estamos testando se há diferenças nas distribuições da variável numérica entre dois grupos. Formalmente, o teste de hipótese é descrito com uma hipótese nula (H0) e uma hipótese alternativa (H1).

• H0: Não há diferenças nas distribuições da variável de preço entre os grupos Justo e Ideal

• H1 Existem diferenças nas distribuições da variável preço entre os grupos Justo e Ideal

O seguinte pode ser implementado em R com o seguinte código -

t.test(price ~ cut, data = data)

# Welch Two Sample t-test 
#  
# data:  price by cut 
# t = 9.7484, df = 1894.8, p-value < 2.2e-16 
# alternative hypothesis: true difference in means is not equal to 0 
# 95 percent confidence interval: 
#   719.9065 1082.5251 
# sample estimates: 
#   mean in group Fair mean in group Ideal  
#   4358.758            3457.542   

# Another way to validate the previous results is to just plot the 
distributions using a box-plot 
plot(price ~ cut, data = data, ylim = c(0,12000),  
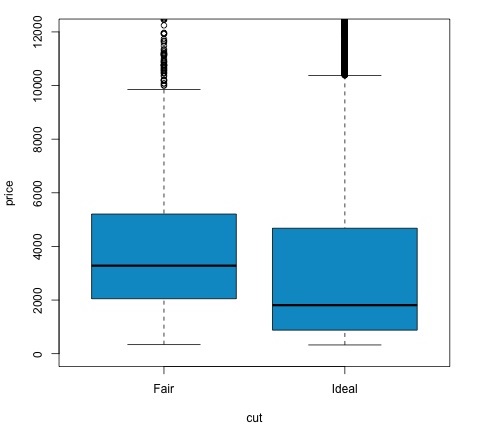
   col = 'deepskyblue3')

Podemos analisar o resultado do teste verificando se o valor p é menor que 0,05. Se for esse o caso, mantemos a hipótese alternativa. Isso significa que encontramos diferenças de preço entre os dois níveis do fator de corte. Pelos nomes dos níveis, esperaríamos esse resultado, mas não esperaríamos que o preço médio no grupo Fail fosse maior do que no grupo Ideal. Podemos ver isso comparando as médias de cada fator.

o plotcomando produz um gráfico que mostra a relação entre o preço e a variável de corte. É um enredo de caixa; cobrimos esse gráfico na seção 16.0.1, mas basicamente mostra a distribuição da variável de preço para os dois níveis de corte que estamos analisando.

Análise de variação

A Análise de Variância (ANOVA) é um modelo estatístico utilizado para analisar as diferenças entre a distribuição dos grupos, comparando a média e a variância de cada grupo, o modelo foi desenvolvido por Ronald Fisher. A ANOVA fornece um teste estatístico para determinar se as médias de vários grupos são iguais ou não e, portanto, generaliza o teste t para mais de dois grupos.

ANOVAs são úteis para comparar três ou mais grupos para significância estatística porque fazer vários testes t de duas amostras resultaria em uma chance maior de cometer um erro estatístico tipo I.

Em termos de fornecer uma explicação matemática, o seguinte é necessário para entender o teste.

x _ij = x + (x _i - x) + (x _ij - x)

Isso leva ao seguinte modelo -

x _ij = μ + α _i + ∈ _ij

onde μ é a grande média e α _i é a i-ésima média do grupo. O termo de erro ∈ _ij é assumido como sendo iid de uma distribuição normal. A hipótese nula do teste é que -

α ₁ = α ₂ =… = α _k

Em termos de cálculo da estatística de teste, precisamos calcular dois valores -

• Soma dos quadrados para diferença entre os grupos -

$$ SSD_B = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {i}}} - \ bar {x}) ^ 2 $$

• Soma dos quadrados dentro dos grupos

$$ SSD_W = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {ij}}} - \ bar {x _ {\ bar {i}}}) ^ 2 $$

onde SSD _B tem um grau de liberdade de k − 1 e SSD _W tem um grau de liberdade de N − k. Em seguida, podemos definir as diferenças médias quadradas para cada métrica.

MS _B = SSD _B / (k - 1)

MS _w = SSD _w / (N - k)

Finalmente, a estatística de teste em ANOVA é definida como a razão das duas quantidades acima

F = MS _B / MS _w

que segue uma distribuição F com k − 1 e N − k graus de liberdade. Se a hipótese nula for verdadeira, F provavelmente seria próximo de 1. Caso contrário, o MSB do quadrado médio entre os grupos provavelmente será grande, o que resulta em um grande valor de F.

Basicamente, ANOVA examina as duas fontes da variância total e vê qual parte contribui mais. É por isso que é chamada de análise de variância, embora a intenção seja comparar as médias dos grupos.

Em termos de cálculo da estatística, é realmente bastante simples de fazer em R. O exemplo a seguir demonstrará como isso é feito e representará graficamente os resultados.

library(ggplot2)
# We will be using the mtcars dataset 

head(mtcars) 
#                    mpg  cyl disp  hp drat  wt  qsec   vs am  gear carb 
# Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4 
# Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4 
# Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1 
# Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1 
# Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2 
# Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1  

# Let's see if there are differences between the groups of cyl in the mpg variable. 
data = mtcars[, c('mpg', 'cyl')]  
fit = lm(mpg ~ cyl, data = mtcars) 
anova(fit)  

# Analysis of Variance Table 
# Response: mpg 
#           Df Sum Sq Mean Sq F value    Pr(>F)     
# cyl        1 817.71  817.71  79.561 6.113e-10 *** 
# Residuals 30 308.33   10.28 
# Signif. codes:  0 *** 0.001 ** 0.01 * 0.05 . 
# Plot the distribution 
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')

O código produzirá a seguinte saída -

O valor de p obtido no exemplo é significativamente menor do que 0,05, então R retorna o símbolo '***' para denotar isso. Isso significa que rejeitamos a hipótese nula e que encontramos diferenças entre as médias de mpg entre os diferentes grupos docyl variável.