Цифровая связь - дельта-модуляция
Частота дискретизации сигнала должна быть выше, чем частота Найквиста, чтобы добиться лучшей дискретизации. Если этот интервал выборки в дифференциальной ИКМ значительно уменьшается, разница амплитуд между выборками очень мала, как если бы разница1-bit quantization, то размер шага будет очень маленьким, т.е. Δ (дельта).
Дельта-модуляция
Тип модуляции, при котором частота дискретизации намного выше, а размер шага после квантования имеет меньшее значение. Δ, такая модуляция называется delta modulation.
Особенности дельта-модуляции
Ниже приведены некоторые особенности дельта-модуляции.
Входной сигнал с избыточной дискретизацией используется для полного использования корреляции сигнала.
Дизайн квантования прост.
Входная последовательность намного выше, чем коэффициент Найквиста.
Качество среднее.
Конструкция модулятора и демодулятора проста.
Лестничная аппроксимация формы выходного сигнала.
Размер шага очень маленький, т.е. Δ (дельта).
Скорость передачи данных может быть определена пользователем.
Это предполагает более простую реализацию.
Дельта-модуляция - это упрощенная форма метода DPCM, также рассматриваемая как 1-bit DPCM scheme. Чем меньше интервал выборки, тем выше корреляция сигнала.
Дельта-модулятор
Дельта-модулятор состоит из 1-битного квантователя и схемы задержки, а также двух схем летоисчисления. Ниже представлена блок-схема дельта-модулятора.
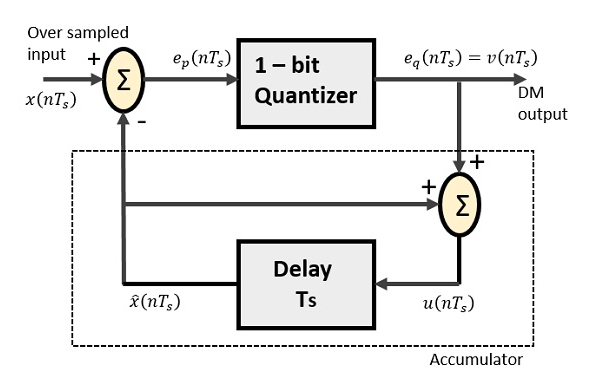
Схема предсказателя в DPCM заменена простой схемой задержки в DM.
Из приведенной выше диаграммы у нас есть обозначения как -
$ x (nT_ {s}) $ = сверхдискретизированный ввод
$ e_ {p} (nT_ {s}) $ = летний выход и вход квантователя
$ e_ {q} (nT_ {s}) $ = выход квантователя = $ v (nT_s) $
$ \ widehat {x} (nT_ {s}) $ = выход схемы задержки
$ u (nT_ {s}) $ = вход схемы задержки
Используя эти обозначения, попробуем теперь разобраться в процессе дельта-модуляции.
$ e_ {p} (nT_ {s}) = x (nT_ {s}) - \ widehat {x} (nT_ {s}) $
--------- уравнение 1
$ = x (nT_ {s}) - u ([n - 1] T_ {s}) $
$ = x (nT_ {s}) - [\ widehat {x} [[n - 1] T_ {s}] + v [[n-1] T_ {s}]] $
--------- уравнение 2
В дальнейшем,
$ v (nT_ {s}) = e_ {q} (nT_ {s}) = S.sig. [e_ {p} (nT_ {s})] $
--------- уравнение 3
$ u (nT_ {s}) = \ widehat {x} (nT_ {s}) + e_ {q} (nT_ {s}) $
Куда,
$ \ widehat {x} (nT_ {s}) $ = предыдущее значение схемы задержки
$ e_ {q} (nT_ {s}) $ = выход квантователя = $ v (nT_s) $
Следовательно,
$ u (nT_ {s}) = u ([n-1] T_ {s}) + v (nT_ {s}) $
--------- уравнение 4
Что значит,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
Предполагая нулевое состояние накопления,
$ U (nT_ {s}) = S \ displaystyle \ sum \ limits_ {j = 1} ^ n sig [e_ {p} (jT_ {s})] $
Accumulated version of DM output = $ \ displaystyle \ sum \ limits_ {j = 1} ^ nv (jT_ {s}) $
--------- уравнение 5
Теперь обратите внимание, что
$ \ widehat {x} (nT_ {s}) = u ([n-1] T_ {s}) $
$ = \ Displaystyle \ сумма \ limits_ {j = 1} ^ {n - 1} v (jT_ {s}) $
--------- уравнение 6
Выходной сигнал блока задержки - это выходной сигнал аккумулятора с отставанием на одну выборку.
Из уравнений 5 и 6 мы получаем возможную структуру демодулятора.
Форма волны, аппроксимированная по лестничной схеме, будет выходом дельта-модулятора с размером шага как дельта (Δ). Качество вывода сигнала среднее.
Дельта-демодулятор
Дельта-демодулятор состоит из фильтра нижних частот, сумматора и схемы задержки. Здесь исключается схема предсказателя, и, следовательно, на демодулятор не подается предполагаемый входной сигнал.
Ниже представлена диаграмма дельта-демодулятора.
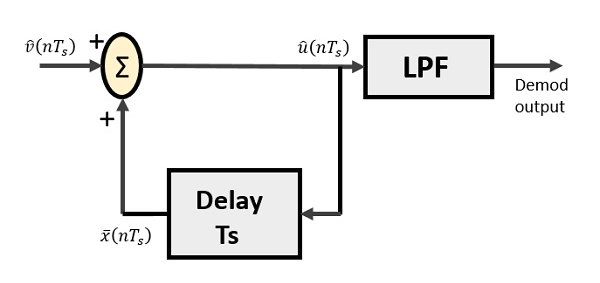
Из приведенной выше диаграммы у нас есть обозначения как -
$ \ widehat {v} (nT_ {s}) $ - входной образец
$ \ widehat {u} (nT_ {s}) $ - летний выход
$ \ bar {x} (nT_ {s}) $ - задержанный вывод
Двоичная последовательность будет подаваться на вход демодулятора. Примерная мощность лестничной клетки выдается на ФНЧ.
Фильтр нижних частот используется по многим причинам, но наиболее заметной причиной является устранение шума для внеполосных сигналов. Ошибка размера шага, которая может возникнуть в передатчике, называетсяgranular noise, который здесь устранен. Если шума нет, то выход модулятора равен входу демодулятора.
Преимущества DM над DPCM
1-битный квантователь
Очень простая конструкция модулятора и демодулятора
Однако в DM есть некоторый шум.
Крутизна Искажение при перегрузке (когда Δ маленький)
Гранулированный шум (когда Δ большой)
Адаптивная дельта-модуляция (ADM)
В цифровой модуляции мы столкнулись с определенной проблемой определения размера шага, который влияет на качество выходной волны.
При крутом наклоне модулирующего сигнала требуется больший размер шага, а при небольшом наклоне сообщения - меньший. Мельчайшие детали упускаются из виду. Таким образом, было бы лучше, если бы мы могли контролировать настройку размера шага в соответствии с нашими требованиями, чтобы получить выборку желаемым образом. Это концепцияAdaptive Delta Modulation.
Ниже представлена блок-схема адаптивного дельта-модулятора.
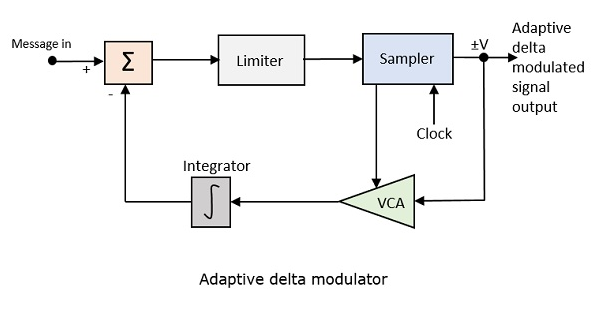
Коэффициент усиления усилителя, управляемого напряжением, регулируется выходным сигналом сэмплера. Коэффициент усиления усилителя определяет размер шага, и оба они пропорциональны.
ADM квантует разницу между значением текущей выборки и предсказанным значением следующей выборки. Он использует переменную высоту шага для прогнозирования следующих значений для точного воспроизведения быстро меняющихся значений.