Цифровая связь - отбор проб
Sampling определяется как «Процесс измерения мгновенных значений сигнала непрерывного времени в дискретной форме».
Sample представляет собой часть данных, взятых из всех данных, которые являются непрерывными во временной области.
Когда источник генерирует аналоговый сигнал и если он должен быть оцифрован, наличие 1s и 0sт.е. высокий или низкий, сигнал должен быть дискретизирован по времени. Эта дискретизация аналогового сигнала называется дискретизацией.
На следующем рисунке показан непрерывный сигнал. x (t) и дискретизированный сигнал xs (t). когдаx (t) умножается на периодическую последовательность импульсов, дискретизированный сигнал xs (t) получается.
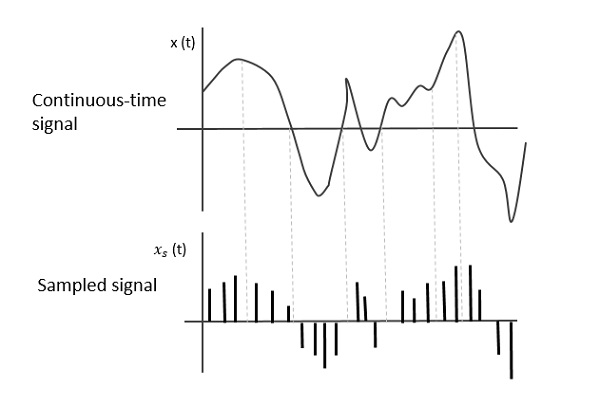
Частота выборки
Для дискретизации сигналов необходимо устранить разрыв между отсчетами. Этот разрыв можно назватьsampling period Ts.
$$ Выборка \: Frequency = \ frac {1} {T_ {s}} = f_s $$Куда,
$ T_ {s} $ - время выборки
$ f_ {s} $ - частота дискретизации или частота дискретизации.
Sampling frequency- величина, обратная периоду выборки. Эту частоту дискретизации можно просто назвать какSampling rate. Частота дискретизации означает количество выборок, взятых в секунду, или для конечного набора значений.
Для восстановления аналогового сигнала из оцифрованного сигнала следует тщательно учитывать частоту дискретизации. Частота выборки должна быть такой, чтобы данные в сигнале сообщения не терялись и не перекрывались. Следовательно, для этого была установлена ставка, называемая ставкой Найквиста.
Рейтинг Найквиста
Предположим, что сигнал ограничен полосой пропускания без частотных компонентов выше, чем WГерц. Это означает,Wсамая высокая частота. Для такого сигнала для эффективного воспроизведения исходного сигнала частота дискретизации должна быть вдвое больше максимальной частоты.
Что значит,
$$ f_ {S} = 2W $$Куда,
$ f_ {S} $ - частота дискретизации
W самая высокая частота
Эта частота дискретизации называется Nyquist rate.
Теорема, названная, теорема выборки, была сформулирована в теории этой нормы Найквиста.
Теорема выборки
Теорема выборки, которую также называют Nyquist theorem, предоставляет теорию достаточной частоты дискретизации с точки зрения полосы пропускания для класса функций с ограниченной полосой пропускания.
Теорема выборки гласит, что «сигнал может быть точно воспроизведен, если он дискретизируется со скоростью fs что более чем в два раза превышает максимальную частоту W. »
Чтобы понять эту теорему дискретизации, давайте рассмотрим сигнал с ограниченной полосой частот, т. Е. Сигнал, значение которого равно non-zero между некоторыми –W и W Герц.
Такой сигнал представлен как $x(f) = 0 for |f\lvert > W$
Для сигнала непрерывного времени x (t), сигнал с ограниченной полосой частот в частотной области, можно представить, как показано на следующем рисунке.
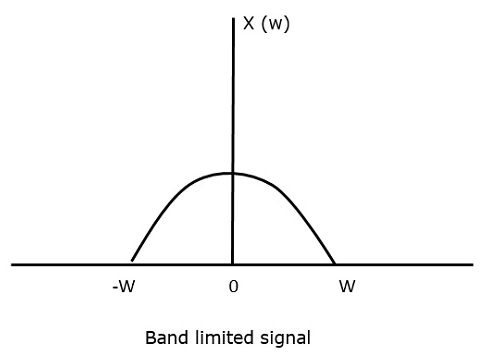
Нам нужна частота дискретизации, частота, при которой не должно быть потери информации даже после выборки. Для этого у нас есть частота Найквиста, при которой частота дискретизации должна быть в два раза больше максимальной частоты. Это критическая частота выборки.
Если сигнал x(t) дискретизируется выше частоты Найквиста, исходный сигнал может быть восстановлен, а если он дискретизируется ниже частоты Найквиста, сигнал не может быть восстановлен.
На следующем рисунке поясняется сигнал, если частота дискретизации выше, чем у 2w в частотной области.
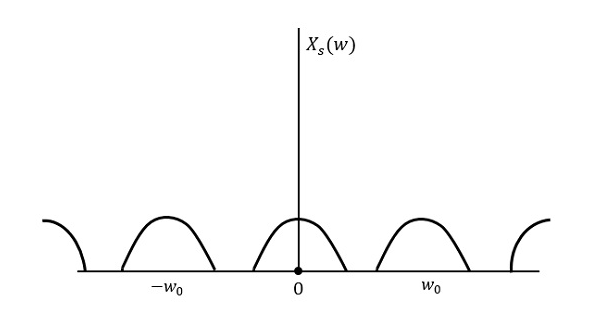
На приведенном выше рисунке показано преобразование Фурье сигнала. $x_{s}(t)$. Здесь информация воспроизводится без потерь. Нет перепутывания, следовательно, восстановление возможно.
Преобразование Фурье сигнала $x_{s}(t)$ является
$$ X_ {s} (w) = \ frac {1} {T_ {s}} \ sum_ {n = - \ infty} ^ \ infty X (w-nw_0) $$Где $ T_ {s} $ = Sampling Period и $ w_ {0} = \ frac {2 \ pi} {T_s} $
Давайте посмотрим, что произойдет, если частота дискретизации будет равна удвоенной максимальной частоте (2W)
Это означает,
$$ f_ {s} = 2W $$Куда,
$ f_ {s} $ - частота дискретизации
W самая высокая частота
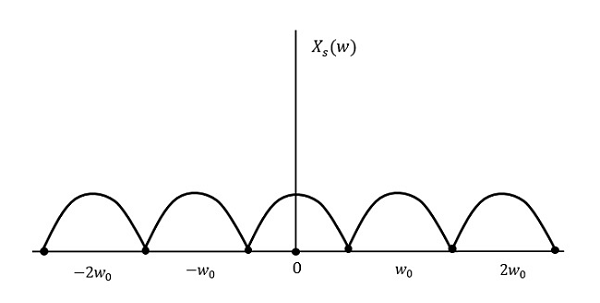
Результат будет таким, как показано на рисунке выше. Информация заменяется без потерь. Следовательно, это также хорошая частота дискретизации.
Теперь давайте посмотрим на условие,
$$ f_ {s} <2W $$Результирующий узор будет выглядеть как на следующем рисунке.

Из вышеприведенного шаблона мы можем наблюдать, что происходит перекрытие информации, что приводит к смешению и потере информации. Это нежелательное явление перекрытия называется сглаживанием.
Сглаживание
Наложение можно назвать «явлением высокочастотной составляющей в спектре сигнала, которая приобретает идентичность низкочастотной составляющей в спектре его дискретизированной версии».
Корректирующие меры, принятые для уменьшения эффекта сглаживания:
В секции передатчика PCM low pass anti-aliasing filter используется перед пробоотборником для устранения нежелательных высокочастотных составляющих.
Сигнал, который дискретизируется после фильтрации, дискретизируется со скоростью, немного превышающей частоту Найквиста.
Выбор более высокой частоты дискретизации, чем частота Найквиста, также помогает упростить дизайн reconstruction filter на приемнике.
Объем преобразования Фурье
Обычно наблюдается, что мы ищем помощи рядов Фурье и преобразований Фурье при анализе сигналов, а также при доказательстве теорем. Потому что -
Преобразование Фурье - это расширение ряда Фурье для непериодических сигналов.
Преобразование Фурье - это мощный математический инструмент, который помогает просматривать сигналы в различных областях и помогает легко анализировать сигналы.
Любой сигнал может быть разложен на сумму синусов и косинусов с использованием этого преобразования Фурье.
В следующей главе давайте обсудим концепцию квантования.