Теория графов - Связность
Возможность пересечения графа от одной вершины к другой определяется тем, как граф связан. Связность - это базовое понятие в теории графов. Связность определяет, подключен ли граф или нет. Он имеет подтемы, основанные на ребре и вершине, известные как связность ребер и связь вершин. Обсудим их подробнее.
Связь
Граф называется connected if there is a path between every pair of vertex. От каждой вершины к любой другой вершине должен пройти некоторый путь. Это называется связностью графа. Граф с несколькими несвязными вершинами и ребрами называется несвязным.
Example 1
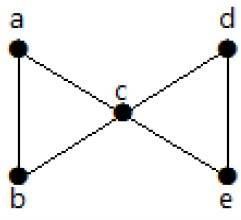
В следующем графе можно перемещаться из одной вершины в любую другую. Например, можно перейти от вершины «а» к вершине «е» по пути «ab-e».
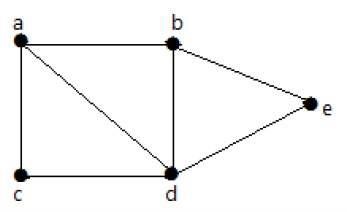
Example 2
В следующем примере переход от вершины «a» к вершине «f» невозможен, поскольку прямой или косвенный путь между ними отсутствует. Следовательно, это несвязный граф.
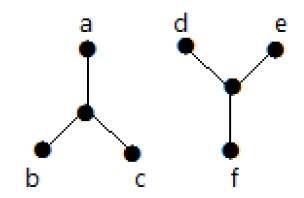
Вырезать вершину
Пусть G - связный граф. Вершина V ∈ G называется вырезанной вершиной графа 'G', если 'G-V' (удалить 'V' из 'G') приводит к несвязному графу. Удаление вырезанной вершины из графа разбивает его на два или более графа.
Note - Удаление вырезанной вершины может привести к отключению графа.
Связный граф «G» может иметь не более (n – 2) разрезанных вершин.
Example
В следующем графе вершины «e» и «c» являются вершинами разреза.

Если удалить «e» или «c», график станет несвязным.

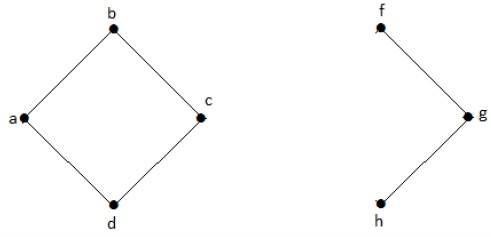
Без «g» не существует пути между вершиной «c» и вершиной «h» и многими другими. Следовательно, это несвязный граф с вырезанной вершиной как 'e'. Точно так же 'c' также является вырезанной вершиной для указанного выше графа.
Cut Edge (мост)
Пусть G - связный граф. Ребро 'e' ∈ G называется разрезанным, если 'G-e' приводит к несвязному графу.
Если удаление ребра в графе приводит к появлению двух или более графов, то это ребро называется Cut Edge.
Example
На следующем графике срезанное ребро - [(c, e)].

Удалив ребро (c, e) из графа, он становится несвязным графом.


В приведенном выше графе удаление ребра (c, e) разбивает граф на два, которые являются не чем иным, как несвязным графом. Следовательно, ребро (c, e) является разрезанным ребром графа.
Note - Пусть 'G' - связный граф с 'n' вершинами, тогда
отрезанное ребро e ∈ G тогда и только тогда, когда ребро 'e' не является частью какого-либо цикла в G.
максимально возможное количество обрезанных кромок - n-1.
всякий раз, когда существуют отрезанные ребра, существуют также отрезанные вершины, потому что по крайней мере одна вершина отрезанного ребра является отрезанной вершиной.
если вырезанная вершина существует, то обрезанное ребро может существовать, а может и не существовать.
Вырезать набор графа
Пусть 'G' = (V, E) - связный граф. Подмножество E 'в E называется разрезанным множеством G, если удаление всех ребер E' из G приводит к разъединению G.
Если удаление определенного количества ребер из графа делает его несвязным, то эти удаленные ребра называются вырезанным множеством графа.
Example
Взгляните на следующий график. Его разрезанное множество E1 = {e1, e3, e5, e8}.
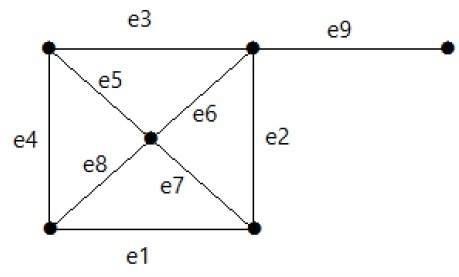
После удаления набора разрезов E1 с графика это будет выглядеть следующим образом:
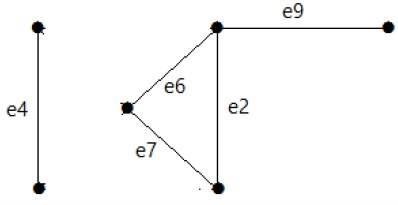
Точно так же есть другие наборы разрезов, которые могут разъединить граф -
E3 = {e9} - Наименьшее сечение графа.
E4 = {e3, e4, e5}
Edge Connectivity
Пусть G - связный граф. Минимальное количество ребер, удаление которых делает G несвязным, называется связностью ребер G.
Notation - λ (G)
Другими словами, number of edges in a smallest cut set of G называется граничной связностью G.
Если у 'G' есть разрезанное ребро, то λ (G) равно 1. (реберная связность G.)
Example
Взгляните на следующий график. После удаления двух минимальных ребер связный граф становится несвязным. Следовательно, его связность ребер (λ (G)) равна 2.
Вот четыре способа отключить граф, удалив два ребра:

Связность вершин
Пусть G - связный граф. Минимальное количество вершин, удаление которых делает «G» либо несвязным, либо сокращает «G» до тривиального графа, называется связностью его вершин.
Notation - К (Г)
Example
В приведенном выше графе удаление вершин «e» и «i» делает граф отключенным.

Если G имеет разрезанную вершину, то K (G) = 1.
Notation - Для любого связного графа G
К (G) ≤ λ (G) ≤ δ (G)
Связность вершин (K (G)), связность ребер (λ (G)), минимальное количество степеней G (δ (G)).
Example
Вычислите λ (G) и K (G) для следующего графика -
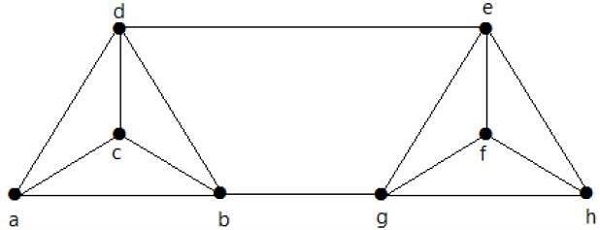
Solution
Из графика
δ (G) = 3
К (G) ≤ λ (G) ≤ δ (G) = 3 (1)
К (Г) ≥ 2 (2)
Удалив ребра {d, e} и {b, h}, мы можем отключить G.
Следовательно,
λ (G) = 2
2 ≤ λ (G) ≤ δ (G) = 2 (3)
Из (2) и (3) связность вершин K (G) = 2