Теория графов - изоморфизм

Граф может существовать в разных формах, имея одинаковое количество вершин, ребер, а также одинаковую связность ребер. Такие графы называются изоморфными графами. Обратите внимание, что мы помечаем графики в этой главе главным образом для того, чтобы ссылаться на них и отличать их друг от друга.

Изоморфные графы

Два графа G ₁ и G ₂ называются изоморфными, если -

• Количество компонентов (вершин и ребер) у них одинаковое.

• Их краевое соединение сохраняется.

Note- Короче говоря, из двух изоморфных графиков один является измененной версией другого. Непомеченный граф также можно рассматривать как изоморфный граф.

There exists a function ‘f’ from vertices of G1 to vertices of G2
   [f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.

Note

Если G ₁ ≡ G _2, то -

| V (G ₁ ) | = | V (G ₂ ) |

| E (G ₁ ) | = | E (G ₂ ) |

Последовательности степеней G ₁ и G ₂ одинаковы.

Если вершины {V ₁ , V ₂ , .. Vk} образуют цикл длины K в G ₁ , то вершины {f (V ₁ ), f (V ₂ ),… f (Vk)} должны образовывать цикл длины K в G ₂ .

Все перечисленные выше условия необходимы для изоморфности графов G ₁ и G ₂ , но недостаточны для доказательства изоморфности графов.

• (G ₁ ≡ G ₂ ) тогда и только тогда, когда (G ₁ - ≡ G ₂ -), где G ₁ и G ₂ - простые графы.

• (G ₁ ≡ G ₂ ), если матрицы смежности G ₁ и G ₂ совпадают.

• (G ₁ ≡ G ₂ ) тогда и только тогда, когда соответствующие подграфы G ₁ и G ₂ (полученные удалением некоторых вершин в G1 и их образов в графе G ₂ ) изоморфны.

Example

Какие из следующих графов изоморфны?

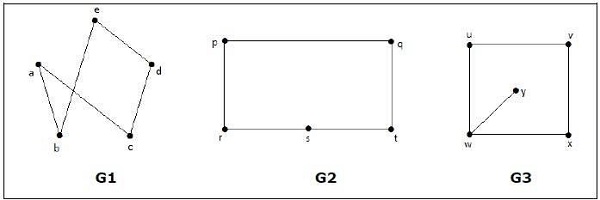
В графе G ₃ вершина w имеет только степень 3, тогда как все остальные вершины графа имеют степень 2. Следовательно, G3 не изоморфна G ₁ или G ₂ .

Взяв дополнения к G ₁ и G ₂ , вы получите -

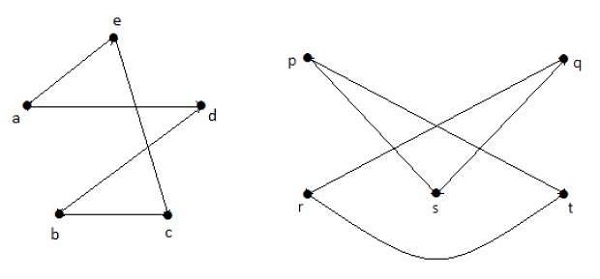
Здесь (G ₁ - ≡ G ₂ -), следовательно (G ₁ ≡ G ₂ ).

Планарные графики

Граф 'G' называется плоским, если его можно нарисовать на плоскости или сфере так, чтобы никакие два ребра не пересекались друг с другом в не вершинной точке.

Example

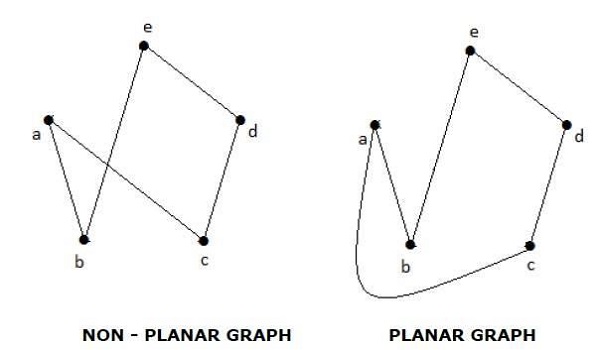
Регионы

Каждый планарный граф делит плоскость на связанные области, называемые регионами.

Example

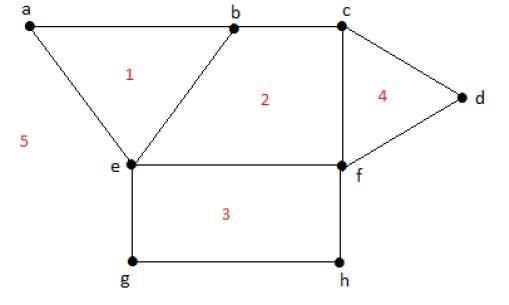
Степень ограниченного региона r = deg(r) = Количество ребер, охватывающих области r.

deg(1) = 3
deg(2) = 4
deg(3) = 4

deg(4) = 3
deg(5) = 8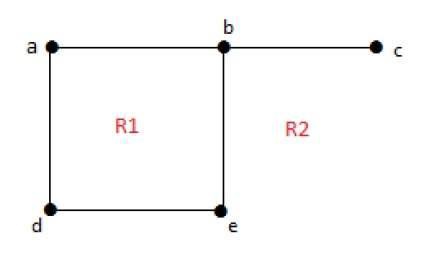

Степень неограниченного региона r = deg(r) = Количество ребер, охватывающих области r.

deg(R1) = 4
deg(R2) = 6

В планарных графах сохраняются следующие свойства:

В плоском графе с n вершинами сумма степеней всех вершин равна -

n Σ i = 1 град (V _i ) = 2 | E |

В соответствии с Sum of Degrees of Regions/ Теорема, в плоском графе с n областями сумма степеней областей -

n Σ i = 1 deg (ri) = 2 | E |

Основываясь на приведенной выше теореме, вы можете сделать следующие выводы -

В плоском графе

Если степень каждой области равна K, то сумма степеней областей равна -

K | R | = 2 | E |

Если степень каждой области не меньше K (≥ K), то

K | R | ≤ 2 | E |

Если степень каждой области не превышает K (≤ K), то

K | R | ≥ 2 | E |

Note - Предположим, что у всех регионов одинаковая степень.

В соответствии с Euler’s Formulae на плоских графах,

Если граф G является связным плоским, то

| V | + | R | = | E | + 2

Если планарный граф с K-компонентами, то

| V | + | R | = | E | + (К + 1)

Где, | V | - количество вершин, | E | - количество ребер, а | R | - количество регионов.

Неравенство вершин края

Если G является связным плоским графом со степенью каждой области не менее K, то

| E | ≤ k / (k-2) {| v | - 2}

Вы знаете, | V | + | R | = | E | + 2

K. | R | ≤ 2 | E |

K (| E | - | V | + 2) ≤ 2 | E |

(K - 2) | E | ≤ К (| V | - 2)

| E | ≤ k / (k-2) {| v | - 2}

Если G - простой связный планарный граф, то

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

Существует хотя бы одна вершина V • ∈ G такая, что deg (V) ≤ 5.

Если 'G' - простой связный плоский граф (как минимум с двумя ребрами) и без треугольников, то

|E| ≤ {2|V| – 4}

Теорема Куратовского

Граф 'G' непланарен тогда и только тогда, когда 'G' имеет подграф, гомеоморфный K ₅ или K _3,3 .

Гомоморфизм

Два графа G ₁ и G ₂ называются гомоморфными, если каждый из этих графов может быть получен из одного и того же графа 'G', разделив некоторые ребра графа G на большее количество вершин. Взгляните на следующий пример -

Разделите ребро rs на два ребра, добавив одну вершину.

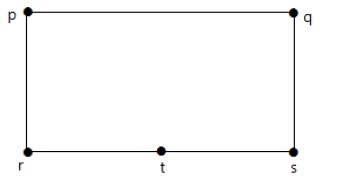
Графики, показанные ниже, гомоморфны первому графу.

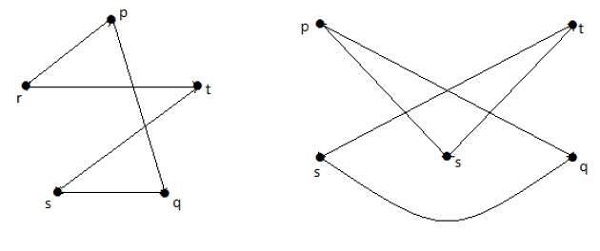
Если G ₁ изоморфен G ₂ , то G гомеоморфен G ₂ , но обратное не обязательно.

• Любой граф с 4 или менее вершинами планарен.

• Любой граф с 8 или менее ребрами является плоским.

• Полный граф K _n планарен тогда и только тогда, когда n ≤ 4.

• Полный двудольный граф K _{m, n} является плоским тогда и только тогда, когда m ≤ 2 или n ≤ 2.

• Простой неплоский граф с минимальным числом вершин - это полный граф K ₅ .

• Простой неплоский граф с минимальным числом ребер - это K _{3, 3} .

Многогранный граф

Простой связный плоский граф называется многогранным графом, если степень каждой вершины ≥ 3, т. Е. Deg (V) ≥ 3 ∀ V ∈ G.

• 3 | V | ≤ 2 | E |

• 3 | R | ≤ 2 | E |