Теория графов - Деревья

Деревья - это графы, не содержащие ни одного цикла. Они представляют собой иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на свою простоту, они имеют богатую структуру.

Деревья предоставляют ряд полезных приложений, от простых, например, генеалогическое древо, до сложных, как деревья в структурах данных в информатике.

Дерево

А connected acyclic graphназывается деревом. Другими словами, связный граф без циклов называется деревом.

Края дерева известны как branches. Элементы деревьев называются их узлами. Узлы без дочерних узлов называютсяleaf nodes.

Дерево с n вершинами имеет n-1 ребер. Если у него на одно ребро больше, чем 'n-1', тогда это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приведет к образованию цикла. Затем он становится циклическим графом, что является нарушением для древовидного графа.

Example 1

Показанный здесь граф представляет собой дерево, потому что у него нет циклов и он связан. Он имеет четыре вершины и три ребра, т. Е. Для "n" вершин "n-1" ребер, как указано в определении.

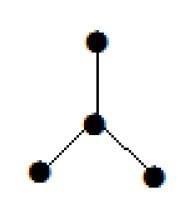
Note - Каждое дерево имеет не менее двух вершин первой степени.

Example 2

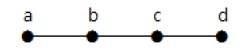
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины «b» и «c» имеют степень два. Это возможно, потому что для того, чтобы цикл не образовывался, в любом месте графа должно быть как минимум два одиночных ребра. Это не что иное, как два ребра со степенью один.

лес

А disconnected acyclic graphназывается лесом. Другими словами, непересекающийся набор деревьев называется лесом.

Example

Следующий график выглядит как два подграфика; но это единый несвязный граф. На этом графике нет циклов. Следовательно, ясно, что это лес.

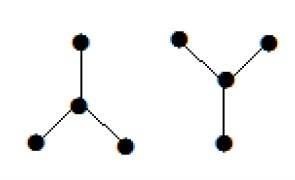
Spanning Trees

Пусть G - связный граф, тогда подграф H графа G называется остовным деревом графа G, если -

• H - дерево
• H содержит все вершины G.

Остовное дерево T неориентированного графа G - это подграф, который включает в себя все вершины графа G.

Example

В приведенном выше примере G - связный граф, а H - подграф G.

Ясно, что в графе H нет циклов, это дерево с шестью ребрами, которое на единицу меньше, чем общее количество вершин. Следовательно, H является остовным деревом группы G.

Рейтинг цепи

Пусть G - связный граф с n вершинами и m ребрами. Остовное дерево T группы G содержит (n-1) ребер.

Следовательно, количество ребер, которое вам нужно удалить из 'G', чтобы получить остовное дерево, = m- (n-1), которое называется рангом схемы G.

Эта формула верна, потому что в остовном дереве должно быть n-1 ребер. Из m ребер нужно оставить n – 1 ребер в графе.

Следовательно, удаление «n – 1» ребер из «m» дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.

Example

Взгляните на следующий график -

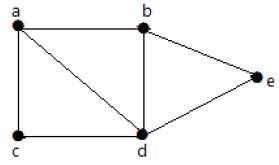
Для графа, приведенного в приведенном выше примере, у вас m = 7 ребер и n = 5 вершин.

Тогда ранг схемы -

G = т - (п - 1)

= 7 - (5-1)

= 3

Example

Пусть 'G' - связный граф с шестью вершинами и степенью каждой вершины три. Найдите ранг цепи "G".

По теореме о сумме степеней вершин

n Σ i=1deg (V _i ) = 2 | E |

6 × 3 = 2 | E |

| E | = 9

Ранг цепи = | E | - (| V | - 1)

= 9 - (6-1) = 4

Теорема Кирхгофа

Теорема Кирхгофа полезна для определения количества остовных деревьев, которые могут быть образованы из связного графа.

Example

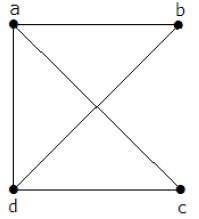
Матрица «A» должна быть заполнена так, как если есть ребро между двумя вершинами, то оно должно быть указано как «1», иначе «0».

$$ A = \ begin {vmatrix} 0 & a & b & c & d \\ a & 0 & 1 & 1 & 1 \\ b & 1 & 0 & 0 & 1 \\ c & 1 & 0 & 0 & 1 \\ d & 1 & 1 & 1 & 0 \ end {vmatrix} = \ begin {vmatrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \ end {vmatrix} $$

Используя теорему Кирхгофа, ее следует изменить, заменив основные диагональные значения степенью вершин, а все остальные элементы - на -1.

$$ = \ begin {vmatrix} 3 & -1 & -1 & -1 \\ - 1 & 2 & 0 & -1 \\ - 1 & 0 & 2 & -1 \\ - 1 & -1 & -1 & 3 \ end {vmatrix} = M $$ $$ M = \ begin {vmatrix} 3 & -1 & -1 & -1 \\ - 1 & 2 & 0 & -1 \\ - 1 & 0 & 2 & -1 \\ - 1 & -1 & -1 & 3 \ end {vmatrix} = 8 $$ $$ Co \: \: factor \: \: of \: \: m1 \: \: = \ begin {vmatrix } 2 & 0 & -1 \\ 0 & 2 & -1 \\ - 1 & -1 & 3 \ end {vmatrix} $$

Таким образом, количество остовных деревьев = 8.