Теория графов - основы

График - это диаграмма точек и линий, соединенных с точками. У него есть по крайней мере одна линия, соединяющая набор из двух вершин, но ни одна вершина не соединяется сама с собой. Концепция графов в теории графов основана на некоторых основных терминах, таких как точка, линия, вершина, ребро, степень вершин, свойства графов и т. Д. Здесь, в этой главе, мы рассмотрим эти основы теории графов.

Точка

A point- это конкретное положение в одномерном, двухмерном или трехмерном пространстве. Для лучшего понимания точку можно обозначить алфавитом. Его можно обозначить точкой.

пример

Здесь точка - это точка с именем «а».

Линия

А Lineэто связь между двумя точками. Его можно представить сплошной линией.

Example

Здесь «a» и «b» - это точки. Связь между этими двумя точками называется линией.

Вершина

Вершина - это точка пересечения нескольких линий. Его также называютnode. Как и точки, вершина также обозначается алфавитом.

Example

Здесь вершина названа алфавитом «а».

Край

Ребро - это математический термин, обозначающий линию, соединяющую две вершины. Из одной вершины можно образовать множество ребер. Без вершины не может быть образовано ребро. Для ребра должны быть начальная и конечная вершины.

Example

Здесь «a» и «b» - две вершины, а связь между ними называется ребром.

График

Граф 'G' определяется как G = (V, E), где V - это множество всех вершин, а E - множество всех ребер в графе.

Example 1

В приведенном выше примере ab, ac, cd и bd - это ребра графа. Аналогично, a, b, c и d - вершины графа.

Example 2

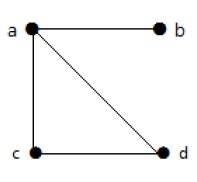
В этом графе четыре вершины a, b, c и d и четыре ребра ab, ac, ad и cd.

Петля

Если в графе ребро проведено от вершины к самому себе, это называется петлей.

Example 1

В приведенном выше графе V - это вершина, у которой есть ребро (V, V), образующее петлю.

Example 2

В этом графе есть две петли, которые образуются в вершине a и вершине b.

Степень вершины

Это количество вершин, смежных с вершиной V.

Notation - град (V).

В простом графе с числом вершин n степень любых вершин равна -

deg (v) ≤ n - 1 ∀ v ∈ G

Вершина может образовывать ребро со всеми остальными вершинами, кроме самой себя. Таким образом, степень вершины будет доnumber of vertices in the graph minus 1. Это 1 для собственной вершины, поскольку она не может образовывать петлю сама по себе. Если в какой-либо из вершин есть петля, то это не простой граф.

Степень вершины можно рассматривать в двух случаях графов -

• Ненаправленный граф

• Направленный график

Степень вершины неориентированного графа

Неориентированный граф не имеет ориентированных ребер. Рассмотрим следующие примеры.

Example 1

Взгляните на следующий график -

В приведенном выше неориентированном графике

• deg (a) = 2, так как в вершине 'a' пересекаются 2 ребра.

• deg (b) = 3, так как в вершине b пересекаются 3 ребра.

• deg (c) = 1, так как в вершине c образовано 1 ребро

• Итак, c - это pendent vertex.

• deg (d) = 2, так как в вершине d пересекаются 2 ребра.

• deg (e) = 0, так как в вершине e образовано 0 ребер.

• Итак, "е" - это isolated vertex.

Example 2

Взгляните на следующий график -

На приведенном выше графике

deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 и deg (e) = 0.

Вершина «е» - изолированная вершина. Граф не имеет ни одной висячей вершины.

Степень вершины ориентированного графа

В ориентированном графе каждая вершина имеет indegree и outdegree.

Степень графа

• Степень вершины V - это количество ребер, которые входят в вершину V.

• Notation - deg− (V).

Внешняя степень графа

• Степень выхода вершины V - это количество ребер, выходящих из вершины V.

• Notation - град + (V).

Рассмотрим следующие примеры.

Example 1

Взгляните на следующий ориентированный граф. Вершина «а» имеет два ребра, «ad» и «ab», которые выходят наружу. Следовательно, его исходная степень равна 2. Точно так же есть ребро «ga», приближающееся к вершине «a». Следовательно, степень «а» равна 1.

Степень и выход других вершин показаны в следующей таблице -

Вершина	Степень	Outdegree
а	1	2
б	2	0
c	2	1
d	1	1
е	1	1
ж	1	1
г	0	2

Example 2

Взгляните на следующий ориентированный граф. В вершине 'a' есть ребро 'ae', выходящее наружу из вершины 'a'. Следовательно, его исходная степень равна 1. Точно так же у графа есть ребро ba, приближающееся к вершине a. Следовательно, степень «а» равна 1.

Степень и выход других вершин показаны в следующей таблице -

Вершина	Степень	Outdegree
а	1	1
б	0	2
c	2	0
d	1	1
е	1	1

Подвесная вершина

Используя степень вершины, мы получаем два особых типа вершин. Вершина со степенью один называется висячей вершиной.

Example

Здесь, в этом примере, вершина «a» и вершина «b» имеют связное ребро «ab». Таким образом, относительно вершины «a» есть только одно ребро по направлению к вершине «b», и аналогично относительно вершины «b» есть только одно ребро по направлению к вершине «a». Наконец, вершина «a» и вершина «b» имеют одну степень, которая также называется висячей вершиной.

Изолированная вершина

Вершина нулевой степени называется изолированной вершиной.

Example

Здесь вершина «a» и вершина «b» не связаны друг с другом, а также с любыми другими вершинами. Таким образом, степень обеих вершин «a» и «b» равна нулю. Их также называют изолированными вершинами.

Смежность

Вот нормы смежности -

• В графе две вершины называются adjacent, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается единственным ребром, соединяющим эти две вершины.

• В графе два ребра называются смежными, если между ними есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.

Example 1

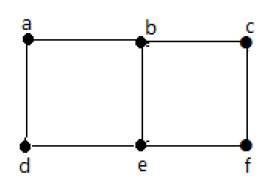
На приведенном выше графике -

• «a» и «b» - смежные вершины, так как между ними есть общее ребро «ab».

• 'a' и 'd' - смежные вершины, так как между ними есть общее ребро 'ad'.

• ab 'и' be '- смежные ребра, так как между ними есть общая вершина' b '.

• be 'и' de '- смежные ребра, так как между ними есть общая вершина' e '.

Example 2

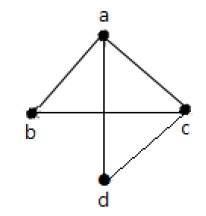
На приведенном выше графике -

• 'a' и 'd' - смежные вершины, так как между ними есть общее ребро 'ad'.

• «c» и «b» - смежные вершины, так как между ними есть общее ребро «cb».

• ad и cd - смежные ребра, так как между ними есть общая вершина d.

• «ac» и «cd» - смежные ребра, так как между ними есть общая вершина «c».

Параллельные края

В графе, если пара вершин соединена более чем одним ребром, эти ребра называются параллельными ребрами.

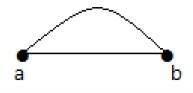
В приведенном выше графе «a» и «b» - это две вершины, которые соединены двумя ребрами «ab» и «ab» между ними. Это называется параллельным ребром.

Мульти График

Граф, имеющий параллельные ребра, известен как мультиграф.

Example 1

В приведенном выше графе пять ребер ab, ac, cd, cd и bd. Поскольку между 'c' и 'd' есть два параллельных ребра, это мультиграф.

Example 2

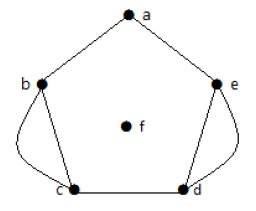
В приведенном выше графе вершины 'b' и 'c' имеют два ребра. Между вершинами «e» и «d» также есть два ребра. Следовательно, это мультиграф.

Градусная последовательность графика

Если степени всех вершин в графе расположены в порядке убывания или возрастания, то полученная последовательность называется последовательностью степеней графа.

Example 1

Вершина	А	б	c	d	е
Присоединенный к	до н.э	объявление	объявление	в, б, д	d
Степень	2	2	2	3	1

В приведенном выше графе для вершин {d, a, b, c, e} последовательность степеней равна {3, 2, 2, 2, 1}.

Example 2

Вершина	А	б	c	d	е	ж
Присоединенный к	быть	а, в	б, г	c, e	объявление	-
Степень	2	2	2	2	2	0

В приведенном выше графе для вершин {a, b, c, d, e, f} последовательность степеней равна {2, 2, 2, 2, 2, 0}.