Конструкция СБИС - МОП-транзистор
Технология комплементарных МОП-транзисторов (CMOS) сегодня широко используется для формирования схем в многочисленных и разнообразных приложениях. Современные компьютеры, центральные процессоры и сотовые телефоны используют CMOS благодаря нескольким ключевым преимуществам. CMOS обеспечивает низкое рассеивание мощности, относительно высокую скорость, высокий запас шума в обоих состояниях и будет работать в широком диапазоне входных и исходных напряжений (при условии, что напряжение источника фиксировано)
Для процессов, которые мы будем обсуждать, доступен тип транзистора - полевой транзистор металл-оксид-полупроводник (MOSFET). Эти транзисторы сформированыas a ‘sandwich’состоящий из полупроводникового слоя, обычно среза или пластины, из монокристалла кремния; слой диоксида кремния (оксид) и слой металла.
Структура полевого МОП-транзистора
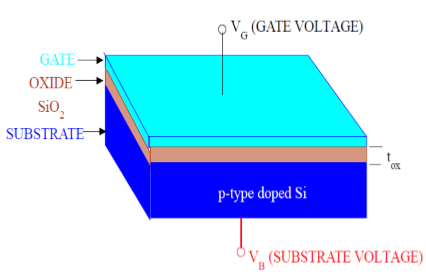
Как показано на рисунке, структура МОП состоит из трех слоев:
The Metal Gate Electrode
The Insulating Oxide Layer (SiO2)
P – type Semiconductor (Substrate)
Структура МОП образует конденсатор, затвор и подложка представляют собой две пластины, а оксидный слой - как диэлектрический материал. Толщина диэлектрического материала (SiO 2 ) обычно составляет от 10 нм до 50 нм. Концентрацией и распределением носителей в подложке можно управлять с помощью внешнего напряжения, подаваемого на затвор и вывод подложки. Теперь, чтобы понять структуру МОП, сначала рассмотрим основные электрические свойства полупроводниковой подложки P-типа.
Концентрация носителя в полупроводниковом материале всегда соответствует Mass Action Law. Закон массового действия дается -
$$ np = n_ {i} ^ {2} $$
Где,
n концентрация носителей электронов
p концентрация носителей дырок
ni - собственная концентрация носителей кремния
Теперь предположим , что субстрат равномерно легированный акцепторной (бор) концентрации N A . Итак, концентрация электронов и дырок в подложке p-типа равна
$$ n_ {po} = \ frac {n_ {i} ^ {2}} {N_ {A}} $$
$$ p_ {po} = N_ {A} $$
Здесь концентрация легирования NAна (от 10 15 до 10 16 см -3 ) больше, чем собственная концентрация ni. Теперь, чтобы понять структуру МОП, рассмотрим диаграмму энергетических уровней кремниевой подложки p-типа.
Как показано на рисунке, ширина запрещенной зоны между зоной проводимости и валентной зоной составляет 1,1 эВ. Здесь потенциал Ферми Φ F - это разность между собственным уровнем Ферми (E i ) и уровнем Ферми (E FP ).
Где уровень Ферми E F зависит от концентрации легирования. Потенциал Ферми Φ F - это разность между собственным уровнем Ферми (E i ) и уровнем Ферми (E FP ).
Математически,
$$ \ Phi_ {Fp} = \ frac {E_ {F} -E_ {i}} {q} $$
Разность потенциалов между зоной проводимости и свободным пространством называется сродством к электрону и обозначается qx.
Таким образом, энергия, необходимая для перехода электрона с уровня Ферми в свободное пространство, называется работой выхода (qΦ S ) и определяется выражением
$$ q \ Phi _ {s} = (E_ {c} -E_ {F}) + qx $$
На следующем рисунке показана диаграмма энергетических зон компонентов, составляющих МОП.
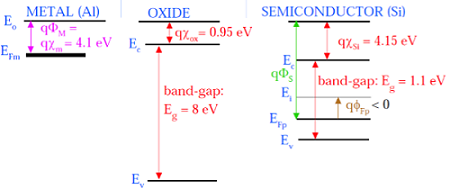
Как показано на приведенном выше рисунке, изолирующий слой SiO 2 имеет большую ширину запрещенной зоны 8 эВ и работу выхода 0,95 эВ. Металлический затвор имеет работу выхода 4,1 эВ. Здесь рабочие функции разные, поэтому это приведет к падению напряжения в системе MOS. На приведенном ниже рисунке показана комбинированная диаграмма энергетических зон МОП-системы.
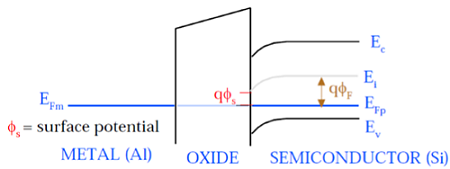
Как показано на этом рисунке, уровни ферми-потенциала металлического затвора и полупроводника (Si) имеют одинаковый потенциал. Потенциал Ферми на поверхности называется поверхностным потенциалом Φ S, и по величине он меньше потенциала Ферми Φ F.
Работа полевого МОП-транзистора
МОП-транзистор состоит из МОП-конденсатора с двумя pn-переходами, закрытыми в области канала, и эта область управляется напряжением на затворе. Чтобы сделать оба pn-перехода смещенными в обратном направлении, потенциал подложки поддерживается ниже, чем потенциал трех других клемм.
Если напряжение затвора будет увеличено сверх порогового напряжения (V GS > V TO ), на поверхности установится инверсионный слой и между истоком и стоком образуется канал n - типа. Этот канал n - типа будет пропускать ток стока в соответствии со значением V DS .
При разном значении V DS полевой МОП-транзистор может работать в разных регионах, как описано ниже.
Линейная область
При V DS = 0 в области перевернутого канала существует тепловое равновесие и ток стока I D = 0. Теперь, если приложено небольшое напряжение стока, V DS > 0, ток стока, пропорциональный V DS , начнет течь от истока к слив через канал.
Канал обеспечивает непрерывный путь прохождения тока от истока к стоку. Этот режим работы называетсяlinear region. Поперечное сечение n-канального MOSFET, работающего в линейной области, показано на рисунке ниже.
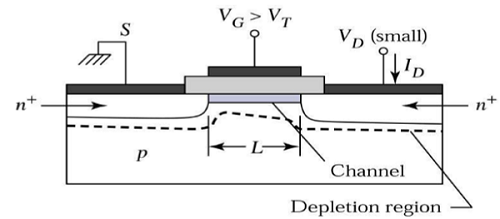
На границе области насыщения
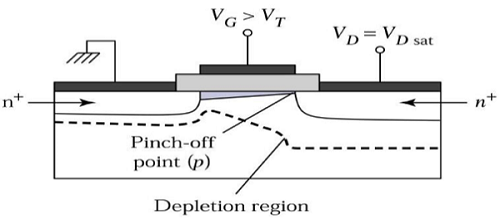
Теперь, если V DS увеличивается, заряды в канале и глубина канала уменьшаются в конце слива. При V DS = V DSAT расходы в канале уменьшаются до нуля, что называетсяpinch – off point. Поперечное сечение n-канального полевого МОП-транзистора, работающего на границе области насыщения, показано на рисунке ниже.
Область насыщенности
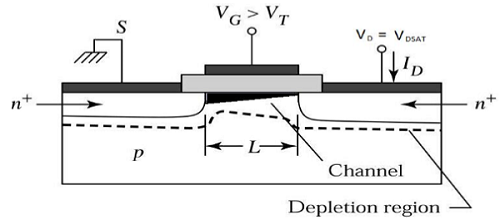
При V DS > V DSAT обедненная поверхность образуется рядом со стоком, и при увеличении напряжения на стоке эта обедненная область распространяется до истока.
Этот режим работы называется Saturation region. Электроны, идущие от истока к концу канала, попадают в область сток-истощение и ускоряются к стоку в сильном электрическом поле.
Ток полевого МОП-транзистора - характеристики напряжения
Чтобы понять вольт-амперную характеристику полевого МОП-транзистора, выполняется аппроксимация для канала. Без этого приближения трехмерный анализ МОП-системы становится сложным. ВGradual Channel Approximation (GCA) для вольт-амперной характеристики уменьшит проблему анализа.
Постепенное приближение канала (GCA)
Рассмотрим поперечный разрез n-канального MOSFET, работающего в линейном режиме. Здесь источник и подложка соединены с землей. В S = V B = 0. Ворота - к - источник (V GS ) и сливом - к - источника напряжения (V DS ) напряжения являются внешние параметры , которые контролируют утечку тока I D .
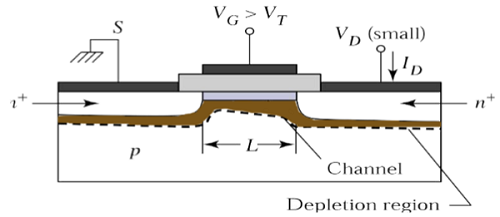
Напряжение V GS устанавливается равным напряжению, превышающему пороговое напряжение V TO , чтобы создать канал между истоком и стоком. Как показано на рисунке, направление по оси x перпендикулярно поверхности, а направление по оси y параллельно поверхности.
Здесь y = 0 на конце источника, как показано на рисунке. Напряжение канала по отношению к источнику представлено какVC(Y). Предположим, что пороговое напряжение VTO постоянно вдоль области канала от y = 0 до y = L. Граничное условие для напряжения V C канала :
$$ V_ {c} \ left (y = 0 \ right) = V_ {s} = 0 \ и \, V_ {c} \ left (y = L \ right) = V_ {DS} $$
Мы также можем предположить, что
$$ V_ {GS} \ geq V_ {TO} $$ и
$$ V_ {GD} = V_ {GS} -V_ {DS} \ geq V_ {TO} $$
Пусть Q1 (y) - полный заряд подвижных электронов в поверхностном инверсионном слое. Этот заряд электрона можно выразить как -
$$ Q1 (y) = - C_ {ox}. [V_ {GS} -V_ {C (Y)} - V_ {TO}] $$
На приведенном ниже рисунке показана пространственная геометрия поверхностного инверсионного слоя и указаны его размеры. Слой инверсии сужается по мере продвижения от стока к истоку. Теперь, если мы рассмотрим небольшую область dy длины канала L, то дополнительное сопротивление dR, обеспечиваемое этой областью, можно выразить как -
$$ dR = - \ frac {dy} {w. \ mu _ {n} .Q1 (y)} $$
Здесь знак минус обусловлен отрицательной полярностью заряда инверсионного слоя Q1, а μ n - поверхностная подвижность, которая постоянна. Теперь подставьте значение Q1 (y) в уравнение dR -
$$ dR = - \ frac {dy} {w. \ mu _ {n}. \ left \ {-C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ right)} \ right ] -V_ {TO} \ right \}} $$
$$ dR = \ frac {dy} {w. \ mu _ {n} .C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ right)} \ right] -V_ {TO} } $$
Теперь падение напряжения в небольшой области dy может быть выражено как
$$ dV_ {c} = I_ {D} .dR $$
Поместите значение dR в приведенное выше уравнение
$$ dV_ {C} = I_ {D}. \ frac {dy} {w. \ mu_ {n} .C_ {ox} \ left [V_ {GS} -V_ {C (Y)} \ right] -V_ {TO}} $$
$$ w. \ mu _ {n} .C_ {ox} \ left [V_ {GS} -V_ {C (Y)} - V_ {TO} \ right] .dV_ {C} = I_ {D} .dy $$
Чтобы получить идентификатор тока стока по всей области канала, приведенное выше уравнение можно проинтегрировать вдоль канала от y = 0 до y = L и напряжений от V C (y) = 0 до V C (y) = V DS ,
$$ C_ {ox} .w. \ Mu _ {n}. \ Int_ {V_ {c} = 0} ^ {V_ {DS}} \ left [V_ {GS} -V_ {C \ left (Y \ right )} - V_ {TO} \ right] .dV_ {C} = \ int_ {Y = 0} ^ {L} I_ {D} .dy $$
$$ \ frac {C_ {ox} .w. \ mu _ {n}} {2} \ left (2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ right) = I_ {D} \ left [L-0 \ right] $$
$$ I_ {D} = \ frac {C_ {ox}. \ Mu _ {n}} {2}. \ Frac {w} {L} \ left (2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ right) $$
Для линейной области V DS <V GS - V TO . Для области насыщения значение V DS больше, чем (V GS - V TO ). Следовательно, для области насыщения V DS = (V GS - V TO ).
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {\ left [2V_ {DS} \ right] V_ {DS} -V_ { DS} ^ {2}} {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {2V_ {DS} ^ {2} -V_ {DS} ^ {2} } {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {V_ {DS} ^ {2}} {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {\ left [V_ {GS} -V_ {TO} \ right] ^ { 2}} {L} \ right) $$