DAA - กราฟหลายขั้นตอน
กราฟหลายขั้นตอน G = (V, E) เป็นกราฟกำกับที่จุดยอดถูกแบ่งออกเป็น k (ที่ไหน k > 1) จำนวนส่วนย่อยที่ไม่ปะติดปะต่อกัน S = {s1,s2,…,sk}เช่นนั้น edge (u, v)อยู่ใน E ดังนั้นu Є s iและv Є s 1 + 1สำหรับเซตย่อยบางส่วนในพาร์ติชันและ |s1| = |sk| = 1.
จุดยอด s Є s1 เรียกว่า source และจุดยอด t Є sk ถูกเรียก sink.
Gมักจะถือว่าเป็นกราฟถ่วงน้ำหนัก ในกราฟนี้ค่าใช้จ่ายของขอบ(ฉัน j)เป็นตัวแทนจากค (I, J) ดังนั้นค่าใช้จ่ายของเส้นทางจากแหล่งที่มาs จม t คือผลรวมของต้นทุนของแต่ละขอบในเส้นทางนี้
ปัญหาของกราฟหลายขั้นตอนคือการค้นหาเส้นทางที่มีต้นทุนขั้นต่ำจากต้นทาง s จม t.
ตัวอย่าง
พิจารณาตัวอย่างต่อไปนี้เพื่อทำความเข้าใจแนวคิดของกราฟหลายขั้นตอน
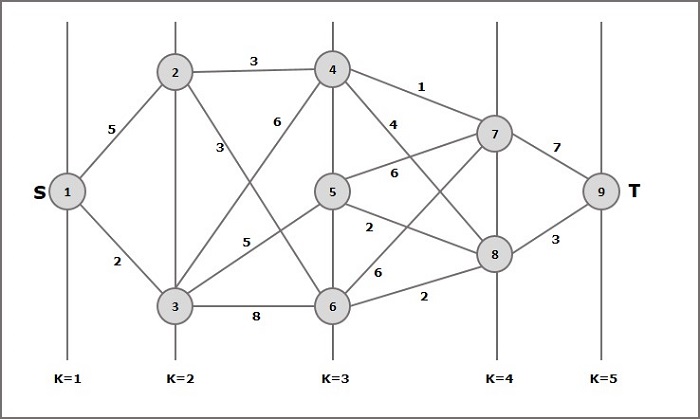
ตามสูตรเราต้องคำนวณต้นทุน (i, j) โดยใช้ขั้นตอนต่อไปนี้
ขั้นตอนที่ 1: ค่าใช้จ่าย (K-2, j)
ในขั้นตอนนี้สามโหนด (โหนด 4, 5. 6) ถูกเลือกเป็น j. ดังนั้นเรามีสามทางเลือกในการเลือกต้นทุนขั้นต่ำในขั้นตอนนี้
ต้นทุน (3, 4) = ขั้นต่ำ {c (4, 7) + ต้นทุน (7, 9), ค (4, 8) + ต้นทุน (8, 9)} = 7
ต้นทุน (3, 5) = ขั้นต่ำ {c (5, 7) + ต้นทุน (7, 9), ค (5, 8) + ต้นทุน (8, 9)} = 5
ต้นทุน (3, 6) = ขั้นต่ำ {c (6, 7) + ต้นทุน (7, 9), ค (6, 8) + ต้นทุน (8, 9)} = 5
ขั้นตอนที่ 2: ค่าใช้จ่าย (K-3, j)
สองโหนดถูกเลือกเป็น j เนื่องจากในระยะ k - 3 = 2 มีสองโหนด 2 และ 3 ดังนั้นค่า i = 2 และ j = 2 และ 3
ต้นทุน (2, 2) = ขั้นต่ำ {c (2, 4) + ต้นทุน (4, 8) + ต้นทุน (8, 9), ค (2, 6) +
ต้นทุน (6, 8) + ต้นทุน (8, 9)} = 8
ต้นทุน (2, 3) = {c (3, 4) + ต้นทุน (4, 8) + ต้นทุน (8, 9), ค (3, 5) + ต้นทุน (5, 8) + ต้นทุน (8, 9), c (3, 6) + ต้นทุน (6, 8) + ต้นทุน (8, 9)} = 10
ขั้นตอนที่ 3: ค่าใช้จ่าย (K-4, j)
ต้นทุน (1, 1) = {c (1, 2) + ต้นทุน (2, 6) + ต้นทุน (6, 8) + ต้นทุน (8, 9), c (1, 3) + ต้นทุน (3, 5) + ต้นทุน (5, 8) + ค่าใช้จ่าย (8, 9))} = 12
c (1, 3) + ต้นทุน (3, 6) + ต้นทุน (6, 8 + ต้นทุน (8, 9))} = 13
ดังนั้นเส้นทางที่มีต้นทุนขั้นต่ำคือ 1→ 3→ 5→ 8→ 9.