NP Hard และ NP-Complete Classes
ปัญหาอยู่ในคลาส NPC ถ้าอยู่ใน NP และเป็น hardเป็นปัญหาใด ๆ ใน NP ปัญหาคือNP-hard หากปัญหาทั้งหมดใน NP สามารถลดเวลาแบบพหุนามได้แม้ว่าจะไม่ได้อยู่ใน NP ก็ตาม
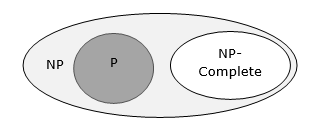
หากมีอัลกอริธึมเวลาพหุนามสำหรับปัญหาใด ๆ เหล่านี้ปัญหาทั้งหมดใน NP จะเป็นเรื่องเวลาพหุนามที่สามารถแก้ไขได้ ปัญหาเหล่านี้เรียกว่าNP-complete. ปรากฏการณ์ของความสมบูรณ์ของ NP มีความสำคัญด้วยเหตุผลทั้งทางทฤษฎีและทางปฏิบัติ
คำจำกัดความของ NP-Completeness
ภาษา B คือ NP-complete หากเป็นไปตามเงื่อนไขสองข้อ
B อยู่ใน NP
ทุก A ใน NP สามารถลดเวลาพหุนามเป็น B.
หากภาษาตรงตามคุณสมบัติที่สอง แต่ไม่จำเป็นต้องเป็นภาษาแรกภาษานั้น B เป็นที่รู้จักกันในชื่อ NP-Hard. ปัญหาในการค้นหาอย่างไม่เป็นทางการB คือ NP-Hard ถ้ามีอยู่บ้าง NP-Complete ปัญหา A ที่ทัวริงลดเป็น B.
ปัญหาใน NP-Hard ไม่สามารถแก้ไขได้ในเวลาพหุนามจนถึง P = NP. หากปัญหาถูกพิสูจน์แล้วว่าเป็น NPC ก็ไม่จำเป็นต้องเสียเวลาในการพยายามค้นหาอัลกอริทึมที่มีประสิทธิภาพสำหรับมัน แต่เราสามารถมุ่งเน้นไปที่อัลกอริธึมการประมาณค่าการออกแบบ
ปัญหา NP-Complete
ต่อไปนี้เป็นปัญหา NP-Complete ซึ่งไม่ทราบอัลกอริทึมเวลาพหุนาม
- การพิจารณาว่ากราฟมีวัฏจักรของแฮมิลตันหรือไม่
- การพิจารณาว่าสูตรบูลีนเป็นที่พอใจหรือไม่ ฯลฯ
ปัญหา NP-Hard
ปัญหาต่อไปนี้คือ NP-Hard
- ปัญหาความน่าพอใจของวงจร
- ตั้งค่าปก
- ปกเวอร์เท็กซ์
- ปัญหาพนักงานขายในการเดินทาง
ในบริบทนี้ตอนนี้เราจะพูดถึง TSP คือ NP-Complete
TSP เป็น NP-Complete
ปัญหาพนักงานขายที่เดินทางประกอบด้วยพนักงานขายและชุดของเมือง พนักงานขายต้องไปเยี่ยมชมเมืองแต่ละเมืองโดยเริ่มจากเมืองหนึ่งและกลับไปที่เมืองเดิม ความท้าทายของปัญหาคือพนักงานขายที่เดินทางต้องการลดระยะเวลารวมของการเดินทางให้น้อยที่สุด
หลักฐาน
เพื่อพิสูจน์ TSP is NP-Completeก่อนอื่นเราต้องพิสูจน์ว่า TSP belongs to NP. ใน TSP เราค้นหาทัวร์และตรวจสอบว่าทัวร์มีจุดยอดแต่ละครั้ง จากนั้นคำนวณต้นทุนทั้งหมดของขอบของทัวร์ สุดท้ายเราจะตรวจสอบว่าต้นทุนต่ำสุดหรือไม่ สิ่งนี้สามารถทำได้ในเวลาพหุนาม ด้วยประการฉะนี้TSP belongs to NP.
ประการที่สองเราต้องพิสูจน์ว่า TSP is NP-hard. เพื่อพิสูจน์สิ่งนี้วิธีหนึ่งคือแสดงให้เห็นว่าHamiltonian cycle ≤p TSP (ดังที่เราทราบว่าปัญหาวงจรแฮมิลตันคือ NPcomplete)
สมมติ G = (V, E) เพื่อเป็นตัวอย่างของวัฏจักรของแฮมิลตัน
ดังนั้นจึงมีการสร้างอินสแตนซ์ของ TSP เราสร้างกราฟที่สมบูรณ์G' = (V, E'), ที่ไหน
$$ E ^ {'} = \ lbrace (i, j) \ โคลอน i, j \ ใน V \: \: และ \: i \ neq j $$
ดังนั้นฟังก์ชันต้นทุนจึงถูกกำหนดดังนี้ -
$$ t (i, j) = \ begin {cases} 0 & if \: (i, j) \: \ in E \\ 1 & else \ end {cases} $$
ตอนนี้สมมติว่าวงจรแฮมิลตัน h มีอยู่ใน G. เป็นที่ชัดเจนว่าต้นทุนของแต่ละขอบในh คือ 0 ใน G' เนื่องจากแต่ละขอบเป็นของ E. ดังนั้น,h มีค่าใช้จ่าย 0 ใน G'. ดังนั้นถ้ากราฟG มีวัฏจักรของแฮมิลตันแล้วกราฟ G' มีทัวร์ของ 0 ค่าใช้จ่าย.
ในทางกลับกันเราถือว่า G' มีทัวร์ h' ค่าใช้จ่ายมากที่สุด 0. ค่าขอบในE' คือ 0 และ 1ตามความหมาย ดังนั้นแต่ละขอบจะต้องมีค่าใช้จ่าย0 เป็นค่าใช้จ่ายของ h' คือ 0. เราจึงสรุปว่าh' มีเฉพาะขอบใน E.
เราได้พิสูจน์แล้วว่า G มีวัฏจักรของแฮมิลตันถ้าและต่อเมื่อ G' มีค่าใช้จ่ายมากที่สุด 0. TSP เป็น NP-complete