DAA - เส้นทางที่สั้นที่สุด

อัลกอริทึมของ Dijkstra

อัลกอริทึมของ Dijkstra แก้ปัญหาเส้นทางที่สั้นที่สุดของแหล่งเดียวบนกราฟถ่วงน้ำหนักกำกับG = (V, E)โดยที่ขอบทั้งหมดไม่เป็นลบ (เช่นw (u, v) ≥ 0 สำหรับแต่ละขอบ(u, v ) Є E )

ในอัลกอริทึมต่อไปนี้เราจะใช้ฟังก์ชันเดียว Extract-Min()ซึ่งแยกโหนดด้วยคีย์ที่เล็กที่สุด

Algorithm: Dijkstra’s-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
S := Ф 
Q := G.V 
while Q ≠ Ф 
   u := Extract-Min (Q) 
   S := S U {u} 
   for each vertex v Є G.adj[u] 
      if v.d > u.d + w(u, v) 
         v.d := u.d + w(u, v) 
         v.∏ := u

การวิเคราะห์

ความซับซ้อนของอัลกอริทึมนี้ขึ้นอยู่กับการใช้ฟังก์ชัน Extract-Min หากใช้ฟังก์ชัน extract min โดยใช้การค้นหาเชิงเส้นความซับซ้อนของอัลกอริทึมนี้คือO(V² + E).

ในอัลกอริทึมนี้ถ้าเราใช้ min-heap ซึ่ง Extract-Min() ฟังก์ชันทำงานเพื่อส่งคืนโหนดจาก Q ด้วยคีย์ที่เล็กที่สุดความซับซ้อนของอัลกอริทึมนี้สามารถลดลงได้อีก

ตัวอย่าง

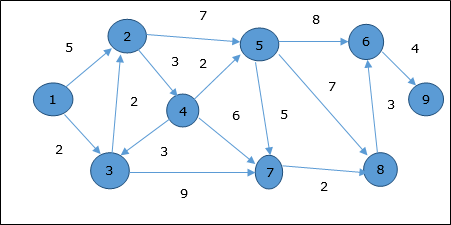
ให้เราพิจารณาจุดยอด 1 และ 9เป็นจุดยอดเริ่มต้นและปลายทางตามลำดับ ในขั้นต้นจุดยอดทั้งหมดยกเว้นจุดยอดเริ่มต้นจะถูกทำเครื่องหมายด้วย∞และจุดยอดเริ่มต้นจะถูกทำเครื่องหมายด้วย0.

จุดยอด	เริ่มต้น	ขั้นตอนที่ 1 V 1	ขั้นตอนที่ 2 V 3	ขั้นตอนที่ 3 V 2	ขั้นตอนที่ 4 V 4	ขั้นตอนที่5 V 5	ขั้นตอนที่6 V 7	ขั้นตอนที่7 V 8	ขั้นตอนที่ 8 V 6
1	0	0	0	0	0	0	0	0	0
2	∞	5	4	4	4	4	4	4	4
3	∞	2	2	2	2	2	2	2	2
4	∞	∞	∞	7	7	7	7	7	7
5	∞	∞	∞	11	9	9	9	9	9
6	∞	∞	∞	∞	∞	17	17	16	16
7	∞	∞	11	11	11	11	11	11	11
8	∞	∞	∞	∞	∞	16	13	13	13
9	∞	∞	∞	∞	∞	∞	∞	∞	20

ดังนั้นระยะทางต่ำสุดของจุดยอด 9 จากจุดยอด 1 คือ 20. และเส้นทางคือ

1 → 3 → 7 → 8 → 6 → 9

เส้นทางนี้ถูกกำหนดโดยอิงจากข้อมูลรุ่นก่อน

อัลกอริทึม Bellman Ford

อัลกอริทึมนี้แก้ปัญหาเส้นทางที่สั้นที่สุดของแหล่งเดียวของกราฟกำกับ G = (V, E)ซึ่งน้ำหนักขอบอาจเป็นลบ ยิ่งไปกว่านั้นอัลกอริทึมนี้สามารถใช้เพื่อค้นหาเส้นทางที่สั้นที่สุดได้หากไม่มีวงจรถ่วงน้ำหนักเชิงลบใด ๆ

Algorithm: Bellman-Ford-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
for i = 1 to |G.V| - 1 
   for each edge (u, v) Є G.E 
      if v.d > u.d + w(u, v) 
         v.d := u.d +w(u, v) 
         v.∏ := u 
for each edge (u, v) Є G.E 
   if v.d > u.d + w(u, v) 
      return FALSE 
return TRUE

การวิเคราะห์

ครั้งแรก for loop ใช้สำหรับการเริ่มต้นซึ่งทำงานใน O(V)ครั้ง. ต่อไปfor วนรอบ |V - 1| ผ่านขอบซึ่งใช้เวลาO(E) ครั้ง.

ดังนั้นอัลกอริทึม Bellman-Ford จึงทำงาน O(V, E) เวลา.

ตัวอย่าง

ตัวอย่างต่อไปนี้แสดงวิธีการทำงานของอัลกอริทึม Bellman-Ford ทีละขั้นตอน กราฟนี้มีขอบลบ แต่ไม่มีวัฏจักรเชิงลบดังนั้นปัญหาสามารถแก้ไขได้โดยใช้เทคนิคนี้

ในขณะเริ่มต้นจุดยอดทั้งหมดยกเว้นแหล่งที่มาจะถูกทำเครื่องหมายด้วย∞และแหล่งที่มาจะถูกทำเครื่องหมายด้วย 0.

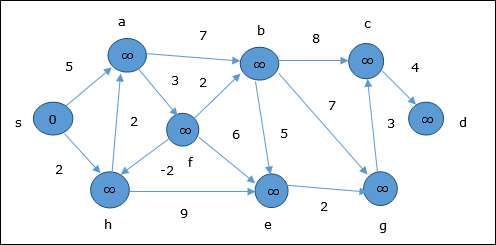
ในขั้นตอนแรกจุดยอดทั้งหมดที่สามารถเข้าถึงได้จากแหล่งที่มาจะได้รับการอัปเดตโดยต้นทุนขั้นต่ำ ดังนั้นจุดยอดa และ h มีการปรับปรุง

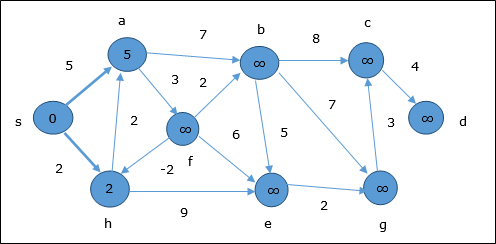
ในขั้นตอนถัดไปจุดยอด a, b, f และ e มีการปรับปรุง

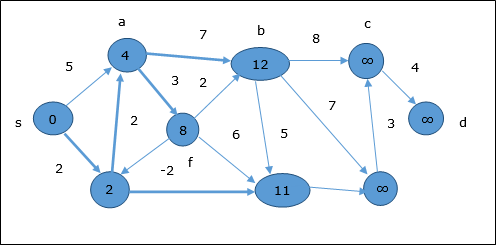
ตามตรรกะเดียวกันในจุดยอดขั้นตอนนี้ b, f, c และ g มีการปรับปรุง

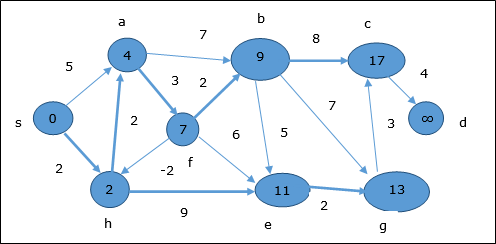
ที่นี่จุดยอด c และ d มีการปรับปรุง

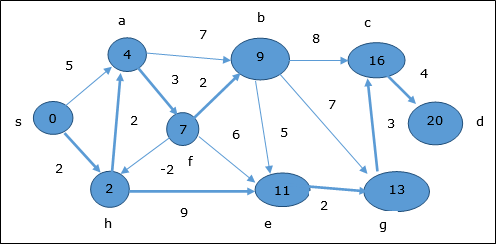
ดังนั้นระยะห่างต่ำสุดระหว่างจุดยอด s และจุดยอด d คือ 20.

จากข้อมูลรุ่นก่อนพา ธ คือ s → h → e → g → c → d