DAA - รูปแบบการผสานที่เหมาะสมที่สุด
รวมชุดไฟล์ที่จัดเรียงที่มีความยาวต่างกันเป็นไฟล์เดียว เราต้องหาวิธีแก้ปัญหาที่ดีที่สุดโดยไฟล์ผลลัพธ์จะถูกสร้างขึ้นในเวลาขั้นต่ำ
หากระบุจำนวนไฟล์ที่จัดเรียงไว้มีหลายวิธีในการรวมเข้าเป็นไฟล์เดียวที่จัดเรียง การผสานนี้สามารถทำได้อย่างชาญฉลาด ดังนั้นการรวมประเภทนี้จึงเรียกว่า2-way merge patterns.
เนื่องจากการจับคู่ที่แตกต่างกันต้องใช้ระยะเวลาที่แตกต่างกันในกลยุทธ์นี้เราต้องการกำหนดวิธีที่ดีที่สุดในการรวมไฟล์จำนวนมากเข้าด้วยกัน ในแต่ละขั้นตอนจะมีการรวมลำดับที่สั้นที่สุดสองลำดับเข้าด้วยกัน
เพื่อรวมไฟล์ p-record file และก q-record file ต้องใช้ p + q บันทึกการเคลื่อนไหวทางเลือกที่ชัดเจนคือรวมไฟล์ที่เล็กที่สุดสองไฟล์เข้าด้วยกันในแต่ละขั้นตอน
รูปแบบการผสานสองทางสามารถแสดงโดยต้นไม้ผสานไบนารี ให้เราพิจารณาชุดของn ไฟล์ที่จัดเรียง {f1, f2, f3, …, fn}. ในขั้นต้นแต่ละองค์ประกอบของสิ่งนี้ถือเป็นต้นไม้ไบนารีโหนดเดียว ในการค้นหาโซลูชันที่เหมาะสมที่สุดนี้จะใช้อัลกอริทึมต่อไปนี้
Algorithm: TREE (n)
for i := 1 to n – 1 do
declare new node
node.leftchild := least (list)
node.rightchild := least (list)
node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight)
insert (list, node);
return least (list);ในตอนท้ายของอัลกอริทึมนี้น้ำหนักของโหนดรูทจะแสดงต้นทุนที่เหมาะสมที่สุด
ตัวอย่าง
ให้เราพิจารณาไฟล์ที่กำหนด f 1 , f 2 , f 3 , f 4และ f 5ด้วยจำนวนองค์ประกอบ 20, 30, 10, 5 และ 30 ตามลำดับ
หากการดำเนินการผสานถูกดำเนินการตามลำดับที่ให้ไว้
M1 = merge f1 and f2 => 20 + 30 = 50
M2 = merge M1 and f3 => 50 + 10 = 60
M3 = merge M2 and f4 => 60 + 5 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
ดังนั้นจำนวนการดำเนินการทั้งหมดคือ
50 + 60 + 65 + 95 = 270
ทีนี้คำถามที่เกิดขึ้นมีทางออกที่ดีกว่านี้หรือไม่?
เรียงลำดับตัวเลขตามขนาดจากน้อยไปหามากเราจะได้ลำดับต่อไปนี้ -
f4, f3, f1, f2, f5
ดังนั้นการดำเนินการผสานสามารถทำได้ในลำดับนี้
M1 = merge f4 and f3 => 5 + 10 = 15
M2 = merge M1 and f1 => 15 + 20 = 35
M3 = merge M2 and f2 => 35 + 30 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
ดังนั้นจำนวนการดำเนินการทั้งหมดคือ
15 + 35 + 65 + 95 = 210
เห็นได้ชัดว่านี่ดีกว่าก่อนหน้านี้
ในบริบทนี้ตอนนี้เรากำลังจะแก้ปัญหาโดยใช้อัลกอริทึมนี้
ชุดเริ่มต้น

ขั้นตอนที่ 1
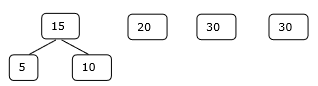
ขั้นตอนที่ 2
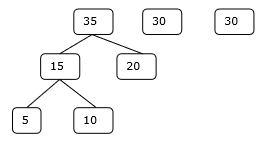
ขั้นตอนที่ 3
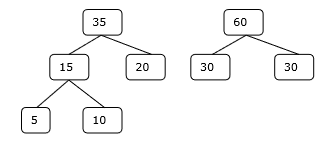
ขั้นตอนที่ 4
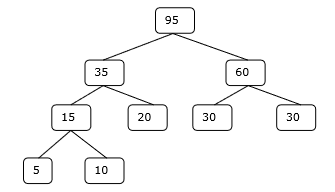
ดังนั้นวิธีแก้ปัญหาจึงใช้เวลา 15 + 35 + 60 + 95 = 205 จำนวนการเปรียบเทียบ