DAA - ต้นไม้ค้นหาไบนารีต้นทุนที่เหมาะสมที่สุด

Binary Search Tree (BST) คือต้นไม้ที่เก็บค่าคีย์ไว้ในโหนดภายใน โหนดภายนอกเป็นโหนดว่าง คีย์จะเรียงลำดับตามศัพท์กล่าวคือสำหรับแต่ละโหนดภายในคีย์ทั้งหมดในแผนผังย่อยด้านซ้ายมีค่าน้อยกว่าคีย์ในโหนดและคีย์ทั้งหมดในแผนผังย่อยด้านขวาจะมีค่ามากกว่า

เมื่อเราทราบความถี่ในการค้นหาแต่ละคีย์แล้วการคำนวณค่าใช้จ่ายที่คาดว่าจะเข้าถึงแต่ละโหนดในโครงสร้างนั้นค่อนข้างง่าย โครงสร้างการค้นหาไบนารีที่ดีที่สุดคือ BST ซึ่งมีต้นทุนที่คาดว่าจะน้อยที่สุดในการค้นหาแต่ละโหนด

เวลาค้นหาขององค์ประกอบใน BST คือ O(n)ในขณะที่เวลาค้นหา Balanced-BST คือ O(log n). อีกครั้งเวลาในการค้นหาสามารถปรับปรุงได้ในโครงสร้างการค้นหาแบบไบนารีต้นทุนที่เหมาะสมโดยวางข้อมูลที่ใช้บ่อยที่สุดในรูทและอยู่ใกล้กับองค์ประกอบรากมากที่สุดในขณะที่วางข้อมูลที่ใช้บ่อยที่สุดไว้ใกล้กับใบไม้และในใบไม้

ที่นี่มีการนำเสนออัลกอริทึมต้นไม้ค้นหาไบนารีที่เหมาะสมที่สุด ขั้นแรกเราสร้าง BST จากชุดที่มีให้n จำนวนคีย์ที่แตกต่างกัน < k₁, k₂, k₃, ... k_n >. ในที่นี้เราถือว่าความน่าจะเป็นในการเข้าถึงคีย์K_i คือ p_i. ปุ่มจำลอง (d₀, d₁, d₂, ... d_n) ถูกเพิ่มเนื่องจากอาจมีการค้นหาบางอย่างสำหรับค่าที่ไม่มีอยู่ในชุดคีย์ K. เราถือว่าสำหรับแต่ละคีย์ดัมมี่d_i ความน่าจะเป็นของการเข้าถึงคือ q_i.

Optimal-Binary-Search-Tree(p, q, n) 
e[1…n + 1, 0…n],  
w[1…n + 1, 0…n], 
root[1…n + 1, 0…n]  
for i = 1 to n + 1 do 
   e[i, i - 1] := qi - 1 
   w[i, i - 1] := qi - 1  
for l = 1 to n do 
   for i = 1 to n – l + 1 do 
      j = i + l – 1 e[i, j] := ∞ 
      w[i, i] := w[i, i -1] + pj + qj 
      for r = i to j do 
         t := e[i, r - 1] + e[r + 1, j] + w[i, j] 
         if t < e[i, j] 
            e[i, j] := t 
            root[i, j] := r 
return e and root

การวิเคราะห์

อัลกอริทึมต้องการ O (n³) เวลาตั้งแต่สามที่ซ้อนกัน forใช้ลูป แต่ละลูปเหล่านี้ใช้เวลามากที่สุดn ค่า

ตัวอย่าง

เมื่อพิจารณาจากต้นไม้ต่อไปนี้ค่าใช้จ่ายคือ 2.80 แม้ว่าจะไม่ใช่ผลลัพธ์ที่ดีที่สุด

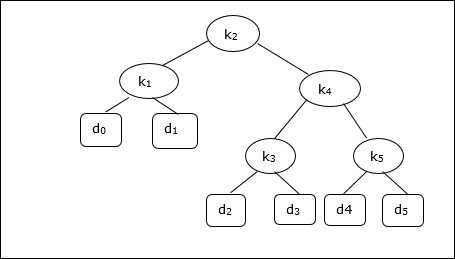
โหนด	ความลึก	ความน่าจะเป็น	เงินสมทบ
k 1	1	0.15	0.30 น
k 2	0	0.10	0.10
k 3	2	0.05	0.15
k 4	1	0.10	0.20
k 5	2	0.20	0.60
ง0	2	0.05	0.15
ง1	2	0.10	0.30 น
ง2	3	0.05	0.20
ง3	3	0.05	0.20
ง4	3	0.05	0.20
ง5	3	0.10	0.40
Total			2.80

เพื่อให้ได้โซลูชันที่ดีที่สุดโดยใช้อัลกอริทึมที่กล่าวถึงในบทนี้ตารางต่อไปนี้จะถูกสร้างขึ้น

ในตารางต่อไปนี้ดัชนีคอลัมน์คือ i และดัชนีแถวคือ j.

จ	1	2	3	4	5	6
5	2.75	2.00	1.30	0.90	0.50	0.10
4	1.75	1.20	0.60	0.30 น	0.05
3	1.25	0.70	0.25	0.05
2	0.90	0.40	0.05
1	0.45	0.10
0	0.05

ว	1	2	3	4	5	6
5	1.00	0.80	0.60	0.50	0.35	0.10
4	0.70	0.50	0.30 น	0.20	0.05
3	0.55	0.35	0.15	0.05
2	0.45	0.25	0.05
1	0.30 น	0.10
0	0.05

ราก	1	2	3	4	5
5	2	4	5	5	5
4	2	2	4	4
3	2	2	3
2	1	2
1	1

จากตารางเหล่านี้สามารถสร้างต้นไม้ที่เหมาะสมที่สุดได้