R - การถดถอยเชิงเส้น
การวิเคราะห์การถดถอยเป็นเครื่องมือทางสถิติที่ใช้กันอย่างแพร่หลายในการสร้างแบบจำลองความสัมพันธ์ระหว่างสองตัวแปร หนึ่งในตัวแปรเหล่านี้เรียกว่าตัวแปรทำนายซึ่งรวบรวมค่าผ่านการทดลอง ตัวแปรอื่นเรียกว่าตัวแปรตอบสนองซึ่งค่าได้มาจากตัวแปรทำนาย
ในการถดถอยเชิงเส้นตัวแปรทั้งสองนี้เกี่ยวข้องกันโดยใช้สมการโดยเลขชี้กำลัง (กำลัง) ของตัวแปรทั้งสองคือ 1 ในทางคณิตศาสตร์ความสัมพันธ์เชิงเส้นแสดงถึงเส้นตรงเมื่อพล็อตเป็นกราฟ ความสัมพันธ์แบบไม่เป็นเชิงเส้นที่เลขชี้กำลังของตัวแปรใด ๆ ไม่เท่ากับ 1 จะสร้างเส้นโค้ง
สมการทางคณิตศาสตร์ทั่วไปสำหรับการถดถอยเชิงเส้นคือ -
y = ax + bต่อไปนี้เป็นคำอธิบายของพารามิเตอร์ที่ใช้ -
y คือตัวแปรตอบสนอง
x คือตัวแปรทำนาย
a และ b คือค่าคงที่ซึ่งเรียกว่าสัมประสิทธิ์
ขั้นตอนในการสร้างการถดถอย
ตัวอย่างง่ายๆของการถดถอยคือการทำนายน้ำหนักของบุคคลเมื่อทราบส่วนสูง ในการทำเช่นนี้เราต้องมีความสัมพันธ์ระหว่างความสูงและน้ำหนักของบุคคล
ขั้นตอนในการสร้างความสัมพันธ์คือ -
ทำการทดลองรวบรวมตัวอย่างค่าที่สังเกตได้ของความสูงและน้ำหนักที่สอดคล้องกัน
สร้างแบบจำลองความสัมพันธ์โดยใช้ lm() ฟังก์ชันใน R
ค้นหาค่าสัมประสิทธิ์จากแบบจำลองที่สร้างขึ้นและสร้างสมการทางคณิตศาสตร์โดยใช้สิ่งเหล่านี้
รับข้อมูลสรุปของโมเดลความสัมพันธ์เพื่อทราบค่าเฉลี่ยข้อผิดพลาดในการทำนาย เรียกอีกอย่างว่าresiduals.
ในการทำนายน้ำหนักของบุคคลใหม่ให้ใช้ predict() ฟังก์ชันใน R
ป้อนข้อมูล
ด้านล่างนี้เป็นข้อมูลตัวอย่างที่แสดงถึงการสังเกต -
# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131
# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48lm () ฟังก์ชัน
ฟังก์ชันนี้สร้างแบบจำลองความสัมพันธ์ระหว่างตัวทำนายและตัวแปรตอบสนอง
ไวยากรณ์
ไวยากรณ์พื้นฐานสำหรับ lm() ฟังก์ชันในการถดถอยเชิงเส้นคือ -
lm(formula,data)ต่อไปนี้เป็นคำอธิบายของพารามิเตอร์ที่ใช้ -
formula เป็นสัญลักษณ์ที่แสดงความสัมพันธ์ระหว่าง x และ y
data คือเวกเตอร์ที่จะนำสูตรไปใช้
สร้างแบบจำลองความสัมพันธ์และรับค่าสัมประสิทธิ์
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(relation)เมื่อเรารันโค้ดด้านบนจะให้ผลลัพธ์ดังนี้ -
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-38.4551 0.6746รับข้อมูลสรุปของความสัมพันธ์
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(summary(relation))เมื่อเรารันโค้ดด้านบนจะให้ผลลัพธ์ดังนี้ -
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-6.3002 -1.6629 0.0412 1.8944 3.9775
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -38.45509 8.04901 -4.778 0.00139 **
x 0.67461 0.05191 12.997 1.16e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared: 0.9548, Adjusted R-squared: 0.9491
F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06ทำนาย () ฟังก์ชัน
ไวยากรณ์
ไวยากรณ์พื้นฐานสำหรับการทำนาย () ในการถดถอยเชิงเส้นคือ -
predict(object, newdata)ต่อไปนี้เป็นคำอธิบายของพารามิเตอร์ที่ใช้ -
object คือสูตรที่สร้างขึ้นแล้วโดยใช้ฟังก์ชัน lm ()
newdata คือเวกเตอร์ที่มีค่าใหม่สำหรับตัวแปรทำนาย
คาดการณ์น้ำหนักของบุคคลใหม่
# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
# Find weight of a person with height 170.
a <- data.frame(x = 170)
result <- predict(relation,a)
print(result)เมื่อเรารันโค้ดด้านบนจะให้ผลลัพธ์ดังนี้ -
1
76.22869แสดงภาพการถดถอยแบบกราฟิก
# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)
# Give the chart file a name.
png(file = "linearregression.png")
# Plot the chart.
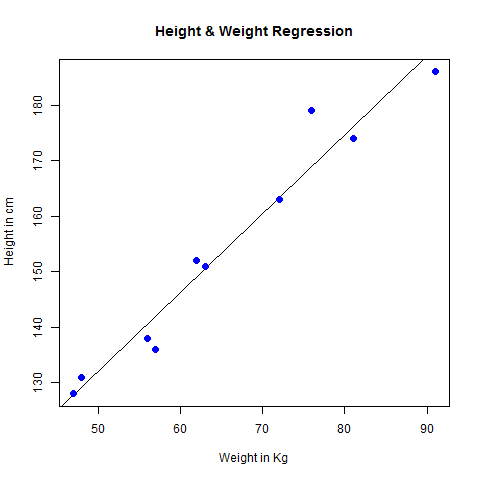
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")
# Save the file.
dev.off()เมื่อเรารันโค้ดด้านบนจะให้ผลลัพธ์ดังนี้ -