İndüktörlerde Devre Bağlantıları
Bir devreye bağlandığında bir Endüktör, bu bağlantı seri veya paralel olabilir. Paralel bağlandıklarında seri olarak da bağlanırlarsa toplam akım, gerilim ve direnç değerlerine ne olacağını şimdi bilelim.
Serideki İndüktörler
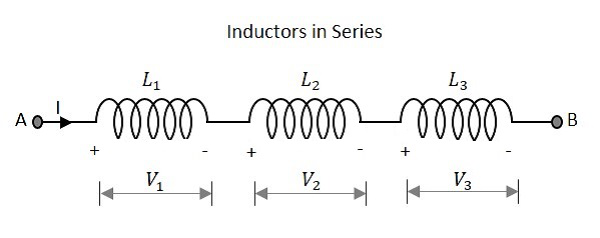
Seri olarak birkaç indüktör bağlandığında ne olduğunu gözlemleyelim. Aşağıdaki şekilde gösterildiği gibi, farklı değerlere sahip üç direnci düşünelim.
İndüktans
Seri indüktörlere sahip bir devrenin toplam endüktansı, bireysel endüktansların toplamına eşittir. Yukarıda verilen şebekenin toplam endüktans değeri
$$ L_ {T} \: \: = \: \: L_ {1} \: \: + \: \: L_ {2} \: \: + \: \: L_ {3} $$
L nerede 1 1 indüktansıdır st direnç, L 2 2 indüktansıdır nd direnç ve L, 3 3 indüktansıdır Rd yukarıda ağda direnç.
Voltaj
Bir seri indüktör ağında görünen toplam voltaj, her bir endüktansa voltaj düşüşlerinin eklenmesidir.
Devre boyunca görünen toplam voltaj
$$ V \: \: = \: \: V_ {1} \: \: + \: \: V_ {2} \: \: + \: \: V_ {3} $$
V burada 1 1 voltaj düşüşü olan st indüktör, V 2 2 voltaj düşüşü olan nd indüktör ve V, 3 3 voltaj düşüşü olduğu Rd yukarıda ağ içinde yer alan indüktörden.
Güncel
Seri bağlı bir dizi indüktörden akan toplam Akım miktarı, ağdaki tüm noktalarda aynıdır.
Ağ üzerinden Akım
$$ I \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
Nerede 1 1 üzerindeki akımdır st indüktör, ben 2 2 üzerindeki akımdır nd indüktör ve ben 3 3 üzerindeki akımdır rd yukarıdaki ağda indüktör.
Paralel İndüktörler
Paralel olarak birkaç direnç bağlandığında ne olduğunu gözlemleyelim. Aşağıdaki şekilde gösterildiği gibi, farklı değerlere sahip üç direnci düşünelim.

İndüktans
Paralel dirençlere sahip bir devrenin toplam endüktansı, seri indüktör ağ yönteminden farklı şekilde hesaplanır. Burada, bireysel endüktansların karşılıklı (1 / R) değeri, toplam endüktans değerini elde etmek için cebirsel toplamın tersi ile eklenir.
Ağın toplam endüktans değeri
$$ \ frac {1} {L_ {T}} \: \: = \: \: \ frac {1} {L_ {1}} \: \: + \: \: \ frac {1} {L_ { 2}} \: \: + \: \: \ frac {1} {L_ {3}} $$
L nerede 1 1 indüktansıdır st indüktör, L 2 2 indüktansıdır nd indüktör ve L, 3 3 indüktansıdır Rd yukarıda ağ içinde yer alan indüktörden.
Paralel endüktansı hesaplamak için kullandığımız yöntemden, iki indüktörlü paralel ağ için basit bir denklem türetebiliriz. Bu
$$ L_ {T} \: \: = \: \: \ frac {L_ {1} \: \: \ times \: \: L_ {2}} {L_ {1} \: \: + \: \ : L_ {2}} $$
Voltaj
Bir Paralel indüktör ağında görünen toplam voltaj, her bir endüktansdaki voltaj düşüşleriyle aynıdır.
Devre boyunca görünen Voltaj
$$ V \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
V burada 1 1 voltaj düşüşü olan st indüktör, V 2 2 voltaj düşüşü olan nd indüktör ve V, 3 3 voltaj düşüşü olduğu Rd yukarıda ağ içinde yer alan indüktörden. Dolayısıyla, paralel bir indüktör ağının tüm noktalarında voltaj aynıdır.
Güncel
Bir Paralel endüktif ağa giren toplam akım miktarı, tüm Paralel dallarda akan tüm bireysel akımların toplamıdır. Her dalın endüktans değeri, içinden geçen akımın değerini belirler.
Ağ üzerinden toplam Akım
$$ I \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
Nerede 1 1 üzerindeki akımdır st indüktör, ben 2 2 üzerindeki akımdır nd indüktör ve ben 3 3 üzerindeki akımdır rd yukarıdaki ağda indüktör.
Bu nedenle, farklı dallardaki bireysel akımların toplamı, paralel bir ağdaki toplam akımı elde eder.
Endüktif reaktans
Endüktif Reaktans, bir indüktörün alternatif akım akışına veya basitçe AC akımına karşı sunduğu muhalefettir. Bir indüktör, akımın akışındaki değişime direnme özelliğine sahiptir ve bu nedenle, şu şekilde adlandırılabilecek bazı muhalefet gösterir.reactancegiriş akımının frekansı da sunduğu dirençle birlikte düşünülmelidir.
Gösterge - XL
Birimler - Ohms
Sembol - Ω
Tamamen endüktif bir devrede, akım IL lagsuygulanan voltaj 90 °. Endüktif reaktans şu şekilde hesaplanır:
$$ X_ {L} \: \: = \: \: 2 \ pi fL $$
F, sinyalin frekansıdır. Dolayısıyla endüktif reaktans, frekans ve endüktansın bir fonksiyonudur.