Temel Elektronik - Endüktans
Bir indüktörün, akım akışının değişmesiyle indüklenen gerilimi elde etme özelliği, Endüktans olarak tanımlanır. Endüktans, voltajın akım değişim hızına oranıdır.
Akımın değişim hızı, manyetik alanda bir değişiklik yaratır, bu da voltaj kaynağına ters yönde bir EMF'yi indükler. EMF'nin indüksiyonunun bu özelliğine,Inductance.
Endüktans formülü
$$ Endüktans \: \: = \: \: \ frac {volatge} {oran \: / \: değişiklik \: \: mevcut} $$
Units −
Endüktans birimi Henry. İle gösterilirL.
İndüktörler çoğunlukla mH (milli Henry) ve μH (mikro Henry) olarak mevcuttur.
Bir bobinin endüktansa sahip olduğu söylenir. one Henry EMF'si one volt Akan akımın bir oranda değiştiği bobinde kendinden indüklenir one ampere per second.
Kendinden Endüktans
İçinde bir miktar akımın aktığı bir bobin düşünülürse, akım akışına dik bir miktar manyetik alana sahiptir. Bu akım değişmeye devam ettiğinde, manyetik alan da değişir ve bu değişen manyetik alan, kaynak voltajının tersine bir EMF'yi indükler. Üretilen bu karşıt EMF,self-induced voltage ve bu yönteme self-inductance.
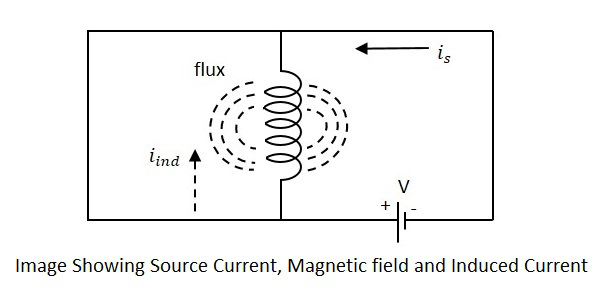
Akım is Şekilde kaynak akımı gösterirken iindindüklenen akımı gösterir. Akı, bobin etrafında oluşturulan manyetik akıyı temsil eder. Gerilim uygulaması ile akımisakışlar ve akış yaratılır. Akım ne zamanis değişir, akı üretilirken değişir iind.
Bobin boyunca indüklenen bu EMF, akımdaki değişim oranı ile orantılıdır. Akımdaki değişim oranı ne kadar yüksekse, indüklenen EMF'nin değeri o kadar yüksek olur.
Yukarıdaki denklemi şu şekilde yazabiliriz:
$$ E \: \: \ alpha \: \: \ frac {dI} {dt} $$
$$ E \: \: = \: \: L \: \: \ frac {dI} {dt} $$
Nerede,
E EMF üretiliyor mu
dI/dt akımın değişim oranını gösterir
L endüktansın ortak etkinliğini gösterir.
Kendi kendine endüktans veya Kendi kendine endüktansın ortak verimliliği şu şekilde adlandırılabilir:
$$ L \: \: = \: \: \ frac {E} {\ frac {dI} {dt}} $$
Gerçek denklem şu şekilde yazılır
$$ E \: \: = \: \: - L \: \: \ frac {dI} {dt} $$
Yukarıdaki denklemdeki eksi şunu gösterir: the EMF is induced in opposite direction to the voltage source Lenz yasasına göre.
Karşılıklı Endüktans
Akım taşıyan bobin, etrafında bir miktar manyetik alan oluşturduğundan, bu bobinin yanına, primerin manyetik akı bölgesinde olacak şekilde başka bir bobin getirilirse, değişen manyetik akı, ikinci bobinde bir EMF'yi indükler. Bu ilk bobin olarak adlandırılırsaPrimary coil, ikincisi bir Secondary coil.
Birincil bobinin değişen manyetik alanı nedeniyle ikincil bobinde EMF indüklendiğinde, böyle bir fenomen olarak adlandırılır. Mutual Inductance.
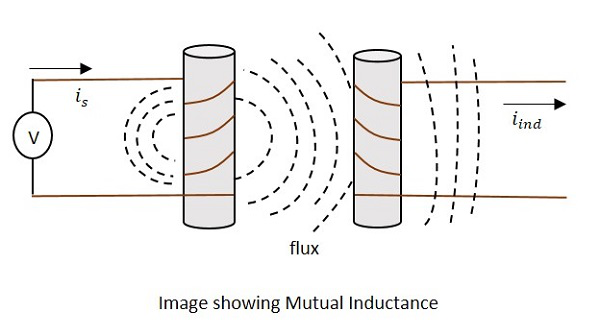
Akım is Şekilde kaynak akımı gösterirken iindindüklenen akımı gösterir. Akı, bobin etrafında oluşturulan manyetik akıyı temsil eder. Bu, ikincil bobine de yayılır.
Gerilim uygulaması ile akım isakışlar ve akış yaratılır. Akım ne zamanis değişir, akı üretilirken değişir iind Karşılıklı endüktans özelliği nedeniyle ikincil bobinde.
Değişim böyle gerçekleşti.
$$ V_ {p} \: \: I_ {p} \ rightarrow \: \: B \: \: \ rightarrow \: \: V_ {s} \: \: I_ {s} $$
Nerede,
Vp ip Sırasıyla Birincil bobindeki Voltaj ve akımı belirtin
B Manyetik akıyı gösterir
Vs is Sırasıyla İkincil bobindeki Voltajı ve akımı belirtin
Karşılıklı endüktans M İki devreden biri, birincil akımdaki değişikliklerle indüklenen sekonderdeki voltaj miktarını açıklar.
$$ V (İkincil) \: \: = \: \: - M \ frac {\ Delta I} {\ Delta t} $$
$ \ Frac {\ Delta I} {\ Delta t} $ akımın zamanla değişim oranı ve MKarşılıklı endüktansın ortak etkinliğidir. Eksi işareti, akımın kaynağa zıt yönünü gösterir.
Units −
Karşılıklı endüktans birimleri
$$ volt \: \: = \: \: M \ frac {amps} {sec} $$
(Yukarıdaki denklemden)
$$ M \: \: = \: \: \ frac {volt. \: Sec} {amp} $$
$$ = \: \: Henry (H) $$
Birincil ve ikincil bobinlerin dönüş sayısına bağlı olarak, manyetik akı bağlantısı ve indüklenen EMF miktarı değişir. Birincildeki dönüş sayısı N1 ile ve ikincil N2 ile gösterilir. Bağlanmanın ortak verimliliği, iki bobinin karşılıklı endüktansını belirten terimdir.
Endüktansı etkileyen faktörler
Bir indüktörün performansını etkileyen birkaç faktör vardır. Başlıca olanlar aşağıda tartışılmaktadır.
Bobinin uzunluğu
İndüktör bobininin uzunluğu, bobinin endüktansı ile ters orantılıdır. Bobinin uzunluğu daha fazlaysa, bu indüktör tarafından sunulan endüktans daha az olur ve bunun tersi de geçerlidir.
Bobinin enine kesit alanı
Bobinin enine kesit alanı, bobinin endüktansı ile doğru orantılıdır. Bobinin alanı ne kadar yüksekse, endüktans o kadar yüksek olacaktır.
Dönüş sayısı
Sargı sayısı ile bobin endüktansı doğrudan etkiler. Endüktans değeri, bobinin sahip olduğu dönüş sayısının karesini alır. Bu nedenle, dönüş sayısı arttıkça, bunun karesi bobinin endüktans değeri olacaktır.
Çekirdeğin geçirgenliği
permeability (μ)İndüktörün çekirdek malzemesi, çekirdeğin kendi içinde bir manyetik alan oluşumu için sağladığı desteği gösterir. higher çekirdek malzemenin geçirgenliği, higher endüktans olacaktır.
Kaplin Katsayısı
Bu, iki bobinin karşılıklı endüktansını hesaplamak için bilinmesi gereken önemli bir faktördür. Sırasıyla N1 ve N2 dönüşlerinin yakın iki bobinini düşünelim.
İlk bobin i 1'den geçen akım bir miktar akı Ψ 1 üretir . Manyetik akı bağlantılarının miktarı weber dönüşleri ile anlaşılır.
Nedeniyle i birim akımına, ikinci bobin, manyetik akı bağlantı miktarını bildirin 1 be
$$ \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Bu, Karşılıklı endüktansın ortak verimliliği olarak anlaşılabilir, yani
$$ M \: \: = \: \: \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Dolayısıyla, iki bobin veya devre arasındaki Karşılıklı endüktansın ortak verimliliği, diğer bobindeki 1A akımdan dolayı bir bobindeki weber dönüşleri olarak anlaşılır.
İlk bobinin kendi kendine endüktansı L 1 ise , o zaman
$$ L_ {1} i_ {1} \: \: = \: \: {N_ {1} \ varphi_ {1}} \: \: => \: \: \ frac {L_ {1}} {N_ {1}} \: \: \ frac {\ varphi_ {1}} {i_ {1}} $$
$$ M \: \: = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} $$
Benzer bir şekilde, geçerli nedeniyle i karşılıklı indüktans katsayısı 2 ikinci bir bobinde bir
$$ M \: \: = \: \: \ frac {N_ {1} \ varphi_ {2}} {i_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \ : 1 $$
İkinci bobinin öz indüktansı L 2 ise
$$ L_ {2} i_ {2} \: \: = \: \: N_ {2} \ varphi_ {2} $$
$$ \ frac {L_ {2}} {N_ {2}} \: \: = \: \: \ frac {\ varphi_ {2}} {i_ {2}} $$
Bu nedenle,
$$ M \: \: = \: \: \ frac {N_ {1} L_ {2}} {N_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \: 2 $$
1 ve 2'yi çarparak,
$$ M \: \: \ times \: \: M = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} \: \: \ times \: \: \ frac { N_ {1} L_ {2}} {N_ {2}} $$
$$ M ^ {2} \: \: = \: \: L_ {1} L_ {2} \: \: => \: \: M \: \: = \: \: \ sqrt {L_ {1 } L_ {2}} $$
İdeal bir durum olan, birincil bobinin tüm değişen akışı ikincil bobin ile bağlandığında yukarıdaki denklem geçerlidir. Ancak pratikte durum böyle değil. Dolayısıyla şöyle yazabiliriz
$$ M \: \: \ neq \: \: \ sqrt {L_ {1} L_ {2}} $$
$$ ve \ frac {M} {\ sqrt {L_ {1} L_ {2}}} \: \: = \: \: K \: \: \ neq \: \: 1 $$
K, kaplin katsayısı olarak bilinir.
Coefficient of coupling K Gerçek karşılıklı endüktans katsayısının ideal (maksimum) karşılıklı endüktans katsayısına oranı olarak tanımlanabilir.
K'nin değeri birliğe yakınsa, bobinlerin sıkı bir şekilde bağlandığı ve k = 0 değeri ise, bobinlerin gevşek bir şekilde bağlandığı söylenir.
İndüktörlerin Uygulamaları
İndüktörlerin birçok uygulaması vardır, örneğin -
Endüktörler, yüksek frekanslı bileşenleri algılamak ve gürültü sinyallerini bastırmak için filtre devrelerinde kullanılır
Devreyi istenmeyen HF sinyallerinden izole etmek için.
İndüktörler, bir transformatör oluşturmak ve devreleri sivri uçlardan izole etmek için elektrik devrelerinde kullanılır.
Endüktörler ayrıca motorlarda da kullanılır.