Dijital İletişim - Hızlı Kılavuz
Günlük hayatımızda gerçekleşen iletişim sinyaller şeklindedir. Ses sinyalleri gibi bu sinyaller genellikle doğaları gereği analogdur. İletişimin belirli bir mesafeden kurulması gerektiğinde, analog sinyaller, etkili iletim için farklı teknikler kullanılarak kablo yoluyla gönderilir.
Dijitalleşmenin Gerekliliği
Geleneksel iletişim yöntemleri, bozulma, parazit ve güvenlik ihlali dahil diğer kayıplar gibi birçok kayıptan muzdarip olan uzun mesafeli iletişimler için analog sinyalleri kullanmıştır.
Bu sorunların üstesinden gelmek için sinyaller farklı teknikler kullanılarak sayısallaştırılır. Sayısallaştırılmış sinyaller, iletişimin kayıpsız daha net ve doğru olmasını sağlar.
Aşağıdaki şekil analog ve dijital sinyaller arasındaki farkı göstermektedir. Dijital sinyaller şunlardan oluşur:1s ve 0s sırasıyla Yüksek ve Düşük değerleri gösterir.

Dijital İletişimin Avantajları
Sinyaller sayısallaştırıldığından, dijital iletişimin analog iletişime göre birçok avantajı vardır, örneğin:
Daha az etkilendikleri için dijital sinyallerdeki bozulma, gürültü ve parazitin etkisi çok daha azdır.
Dijital devreler daha güvenilirdir.
Dijital devrelerin tasarımı kolaydır ve analog devrelerden daha ucuzdur.
Dijital devrelerde donanım uygulaması analogdan daha esnektir.
Çapraz konuşma oluşumu dijital iletişimde çok nadirdir.
Darbenin özelliklerini değiştirmek için yüksek bir parazite ihtiyaç duyması nedeniyle sinyal değiştirilmez, bu çok zordur.
Bilginin gizliliğini korumak için dijital devrelerde şifreleme ve sıkıştırma gibi sinyal işleme fonksiyonları kullanılır.
Hata tespiti ve hata düzeltme kodları kullanılarak hata oluşma olasılığı azaltılır.
Sinyal sıkışmasını önlemek için yayılmış spektrum tekniği kullanılır.
Zaman Bölmeli Çoklama (TDM) kullanarak dijital sinyalleri birleştirmek, Frekans Bölmeli Çoklama (FDM) kullanarak analog sinyalleri birleştirmekten daha kolaydır.
Dijital sinyallerin konfigürasyonu, analog sinyallere göre daha kolaydır.
Dijital sinyaller, analog sinyallere göre daha rahat kaydedilebilir ve alınabilir.
Dijital devrelerin çoğu neredeyse ortak kodlama tekniklerine sahiptir ve bu nedenle benzer cihazlar bir dizi amaç için kullanılabilir.
Kanalın kapasitesi, dijital sinyaller tarafından etkin bir şekilde kullanılır.
Dijital İletişimin Unsurları
Dijital bir iletişim sistemini oluşturan unsurlar, anlaşılma kolaylığı için aşağıdaki blok diyagramla temsil edilmektedir.
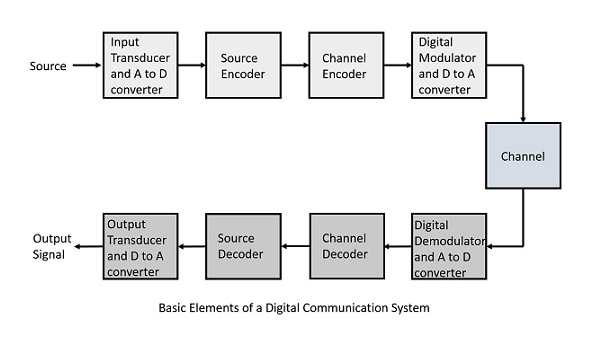
Aşağıda dijital iletişim sisteminin bölümleri yer almaktadır.
Kaynak
Kaynak bir analog sinyal. Example: Bir Ses sinyali
Giriş Dönüştürücü
Bu, fiziksel bir girişi alan ve bunu bir elektrik sinyaline dönüştüren bir dönüştürücüdür (Example: mikrofon). Bu blok aynı zamanda biranalog to digital Daha sonraki işlemler için dijital bir sinyalin gerekli olduğu dönüştürücü.
Dijital bir sinyal genellikle bir ikili dizi ile temsil edilir.
Kaynak Kodlayıcı
Kaynak kodlayıcı, verileri minimum bit sayısına sıkıştırır. Bu süreç, bant genişliğinin etkin kullanımına yardımcı olur. Artık bitleri (gereksiz fazla bitleri, yani sıfırları) kaldırır.
Kanal Kodlayıcı
Kanal kodlayıcı, hata düzeltme için kodlama yapar. Sinyalin iletimi sırasında, kanaldaki gürültü nedeniyle sinyal değişebilir ve bu nedenle bunu önlemek için kanal kodlayıcısı iletilen verilere bazı fazlalık bitler ekler. Bunlar hata düzeltme bitleridir.
Dijital Modülatör
İletilecek sinyal burada bir taşıyıcı tarafından modüle edilir. Sinyal aynı zamanda kanal veya ortam içinde hareket etmesini sağlamak için dijital diziden analoga dönüştürülür.
Kanal
Kanal veya ortam, analog sinyalin verici ucundan alıcı ucuna iletilmesine izin verir.
Dijital Demodülatör
Bu, alıcı sonundaki ilk adımdır. Alınan sinyal demodüle edilir ve tekrar analogdan dijitale dönüştürülür. Sinyal burada yeniden oluşturulur.
Kanal Kod Çözücü
Kanal kod çözücü sekansı tespit ettikten sonra bazı hata düzeltmeleri yapar. İletim sırasında oluşabilecek bozulmalar, bazı yedek bitler eklenerek düzeltilir. Bu bit ilavesi, orijinal sinyalin tamamen kurtarılmasına yardımcı olur.
Kaynak Kod Çözücü
Ortaya çıkan sinyal, bilgi kaybı olmadan saf dijital çıktının elde edilmesi için örnekleme ve niceleme yoluyla bir kez daha sayısallaştırılır. Kaynak kod çözücü, kaynak çıkışını yeniden oluşturur.
Çıkış Dönüştürücü
Bu, sinyali vericinin girişinde bulunan orijinal fiziksel forma dönüştüren son bloktur. Elektrik sinyalini fiziksel çıkışa dönüştürür (Example: hoparlör).
Çıkış sinyali
Bu, tüm süreçten sonra üretilen çıktıdır. Example - Ses sinyali alındı.
Bu birim, giriş, sinyallerin sayısallaştırılması, dijital iletişimin avantajları ve unsurları ile ilgilenmiştir. Önümüzdeki bölümlerde Dijital iletişim kavramlarını detaylı olarak öğreneceğiz.
Modulation mesaj sinyalinin anlık değerlerine göre bir taşıyıcı sinyalin bir veya daha fazla parametresinin değiştirilmesi işlemidir.
Mesaj sinyali, iletişim için iletilen sinyaldir ve taşıyıcı sinyal, veri içermeyen ancak uzun mesafeli iletim için kullanılan yüksek frekanslı bir sinyaldir.
Kullanılan modülasyon tipine göre sınıflandırılan birçok modülasyon tekniği vardır. Hepsinden, kullanılan dijital modülasyon tekniğiPulse Code Modulation (PCM).
Bir sinyal, analog bilgilerini ikili bir diziye dönüştürmek için darbe koduyla modüle edilir, yani, 1s ve 0s. Bir PCM'nin çıktısı ikili bir diziye benzeyecektir. Aşağıdaki şekil, belirli bir sinüs dalgasının anlık değerlerine göre bir PCM çıkışı örneğini göstermektedir.
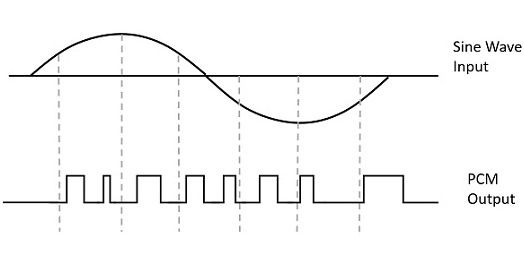
Bir darbe katarı yerine, PCM bir dizi sayı veya rakam üretir ve bu nedenle bu işleme digital. Bu rakamların her biri, ikili kodda olsa da, o andaki sinyal örneğinin yaklaşık genliğini temsil eder.
Darbe Kodu Modülasyonunda, mesaj sinyali bir dizi kodlanmış darbe ile temsil edilir. Bu mesaj sinyali, sinyali hem zaman hem de genlikte ayrı formda temsil ederek elde edilir.
PCM'nin Temel Öğeleri
Darbe Kod Modülatör devresinin verici bölümü şunlardan oluşur: Sampling, Quantizing ve Encoding, analogdan dijitale dönüştürücü bölümünde gerçekleştirilir. Örneklemeden önceki düşük geçiş filtresi, mesaj sinyalinin örtüşmesini önler.
Alıcı bölümündeki temel işlemler regeneration of impaired signals, decoding, ve reconstructionkuantize edilmiş darbe katarı. Aşağıda, hem verici hem de alıcı bölümlerinin temel öğelerini temsil eden PCM'nin blok şeması bulunmaktadır.
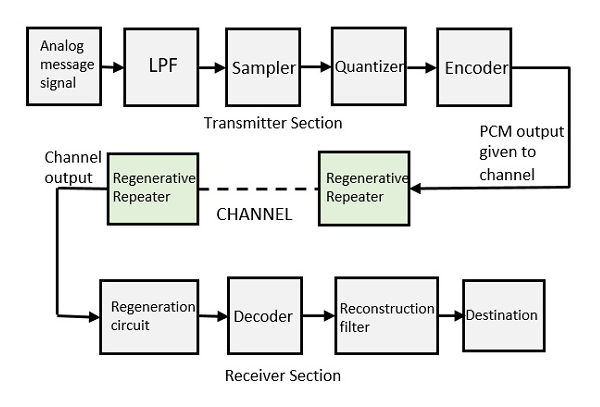
Alçak geçiş filtresi
Bu filtre, mesaj sinyalinin örtüşmesini önlemek için, giriş analog sinyalinde bulunan, mesaj sinyalinin en yüksek frekansından daha büyük olan yüksek frekans bileşenlerini ortadan kaldırır.
Örnekleyici
Bu, orijinal sinyali yeniden oluşturmak için örnek verilerin mesaj sinyalinin anlık değerlerinde toplanmasına yardımcı olan tekniktir. Örnekleme oranı, en yüksek frekans bileşeninin iki katından daha büyük olmalıdırW örnekleme teoremine göre mesaj sinyalinin
Quantizer
Niceleme, aşırı bitleri azaltma ve verileri sınırlama işlemidir. Quantizer'a verildiğinde örneklenen çıktı, fazlalık bitleri azaltır ve değeri sıkıştırır.
Kodlayıcı
Analog sinyalin sayısallaştırılması, kodlayıcı tarafından yapılır. Her nicelenmiş seviyeyi bir ikili kodla belirtir. Burada yapılan örnekleme, örnekleme ve bekletme sürecidir. Bu üç bölüm (LPF, Sampler ve Quantizer) analogdan dijitale dönüştürücü görevi görecektir. Kodlama, kullanılan bant genişliğini en aza indirir.
Rejeneratif Tekrarlayıcı
Bu bölüm sinyal gücünü artırır. Kanalın çıkışı ayrıca sinyal kaybını telafi etmek ve sinyali yeniden oluşturmak ve ayrıca gücünü artırmak için bir rejeneratif tekrarlayıcı devresine sahiptir.
Kod çözücü
Kod çözücü devresi, orijinal sinyali yeniden üretmek için darbe kodlu dalga biçiminin kodunu çözer. Bu devre demodülatör görevi görür.
Yeniden Yapılandırma Filtresi
Rejeneratif devre ve kod çözücü tarafından dijitalden analoğa dönüşüm yapıldıktan sonra, orijinal sinyali geri almak için yeniden yapılandırma filtresi olarak adlandırılan düşük geçişli bir filtre kullanılır.
Bu nedenle, Darbe Kodu Modülatör devresi verilen analog sinyali sayısallaştırır, kodlar ve örnekler ve daha sonra analog bir biçimde iletir. Tüm bu süreç, orijinal sinyali elde etmek için ters bir modelde tekrarlanır.
Sampling "Sürekli zaman sinyalinin anlık değerlerini ayrı bir biçimde ölçme işlemi" olarak tanımlanır.
Sample tüm verilerden alınan ve zaman alanında sürekli olan bir veri parçasıdır.
Bir kaynak bir analog sinyal oluşturduğunda ve bunun sayısallaştırılması gerekiyorsa, 1s ve 0syani, Yüksek veya Düşük, sinyalin zaman içinde ayrıştırılması gerekir. Analog sinyalin bu ayrıklaştırılmasına Örnekleme denir.
Aşağıdaki şekil sürekli zaman sinyalini gösterir x (t) ve örneklenmiş bir sinyal xs (t). Ne zamanx (t) periyodik bir dürtü katarı ile çarpılır, örneklenmiş sinyal xs (t) elde edildi.
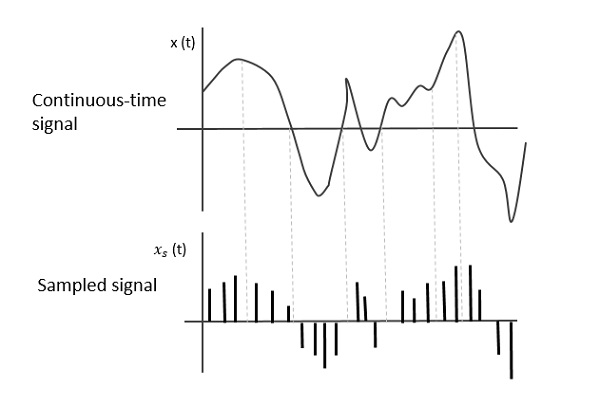
Örnekleme oranı
Sinyalleri ayırmak için numuneler arasındaki boşluk sabitlenmelidir. Bu boşluk şöyle adlandırılabilir:sampling period Ts.
$$ Örnekleme \: Sıklık = \ frac {1} {T_ {s}} = f_s $$
Nerede,
$ T_s $ örnekleme zamanıdır
$ f_s $, örnekleme sıklığı veya örnekleme oranıdır
Sampling frequencyörnekleme süresinin tersidir. Bu örnekleme frekansı, basitçe şöyle adlandırılabilir:Sampling rate. Örnekleme hızı, saniyede veya sınırlı bir değerler kümesi için alınan örneklerin sayısını belirtir.
Bir analog sinyalin sayısallaştırılmış sinyalden yeniden oluşturulabilmesi için, örnekleme oranının yüksek oranda dikkate alınması gerekir. Örnekleme oranı, mesaj sinyalindeki verilerin kaybolmaması veya üst üste binmemesi için olmalıdır. Dolayısıyla Nyquist oranı olarak adlandırılan bunun için bir oran sabitlendi.
Nyquist Oranı
Bir sinyalin bantla sınırlı olduğunu ve daha yüksek frekans bileşenlerinin olmadığını varsayalım. WHertz. Bunun anlamı,Wen yüksek frekanstır. Böyle bir sinyal için, orijinal sinyalin etkili bir şekilde yeniden üretilmesi için, örnekleme hızı en yüksek frekansın iki katı olmalıdır.
Bunun anlamı,
$$ f_S = 2W $$
Nerede,
$ f_S $ örnekleme oranıdır
W en yüksek frekans
Bu örnekleme oranına Nyquist rate.
Bu Nyquist oranının teorisinde Örnekleme Teoremi adlı bir teorem belirtildi.
Örnekleme Teoremi
Örnekleme teoremi olarak da adlandırılır Nyquist theorem, bantlı işlevler sınıfı için bant genişliği açısından yeterli örnekleme oranı teorisini sunar.
Örnekleme teoremi, "bir sinyal, hızda örneklenirse tam olarak yeniden üretilebilir. fs maksimum frekansın iki katından daha büyük olan W. "
Bu örnekleme teoremini anlamak için, bant sınırlı bir sinyali, yani değeri şu olan bir sinyali düşünelim: non-zero bazıları arasında –W ve W Hertz.
Böyle bir sinyal $ x (f) = 0 \: for \: \ mid f \ mid> W $ olarak temsil edilir
Sürekli zaman sinyali için x (t)frekans alanındaki bant sınırlı sinyal, aşağıdaki şekilde gösterildiği gibi temsil edilebilir.
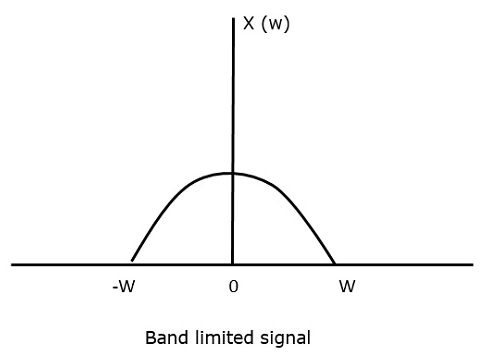
Örneklemeden sonra bile bilgi kaybının olmaması gereken bir örnekleme frekansına ihtiyacımız var. Bunun için, örnekleme frekansının maksimum frekansın iki katı olması gereken Nyquist oranına sahibiz. Kritik örnekleme oranıdır.
Eğer sinyal x(t) Nyquist hızının üzerinde örneklendiğinde, orijinal sinyal geri kazanılabilir ve Nyquist hızının altında örneklenirse sinyal geri kazanılamaz.
Aşağıdaki şekil, daha yüksek bir hızda örneklendiğinde bir sinyali açıklar. 2w frekans alanında.
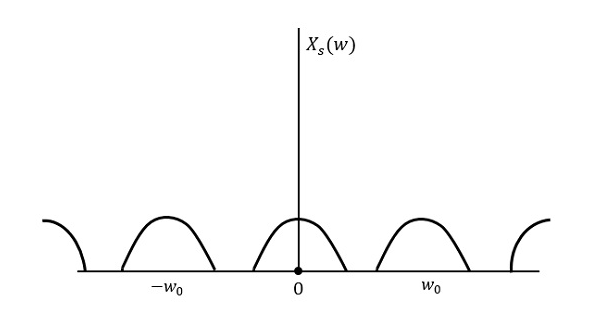
Yukarıdaki şekil bir sinyalin Fourier dönüşümünü göstermektedir xs (t). Burada bilgiler kayıpsız olarak çoğaltılır. Karıştırma yoktur ve dolayısıyla geri kazanım mümkündür.
Sinyalin Fourier Dönüşümü xs (t) dır-dir
$$ X_s (w) = \ frac {1} {T_ {s}} \ sum_ {n = - \ infty} ^ \ infty X (w-nw_0) $$
$ T_s $ = nerede Sampling Period ve $ w_0 = \ frac {2 \ pi} {T_s} $
Örnekleme oranı, en yüksek frekansın iki katına eşitse ne olacağını görelim (2W)
Bunun anlamı,
$$ f_s = 2W $$
Nerede,
$ f_s $ örnekleme sıklığıdır
W en yüksek frekans
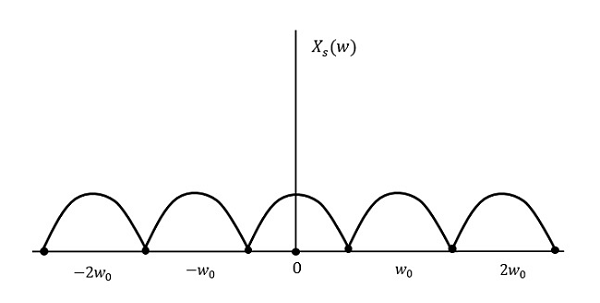
Sonuç, yukarıdaki şekilde gösterildiği gibi olacaktır. Bilgiler herhangi bir kayıp olmaksızın değiştirilir. Dolayısıyla, bu aynı zamanda iyi bir örnekleme oranıdır.
Şimdi duruma bakalım,
$$ f_s <2W $$
Ortaya çıkan desen aşağıdaki şekle benzeyecektir.

Yukarıdaki modelden, bilginin üst üste binmesinin yapıldığını ve bunun da bilgi kaybına ve karıştırmaya yol açtığını gözlemleyebiliriz. Bu istenmeyen üst üste binme olgusuna Aliasing adı verilir.
Aliasing
Takma ad, "örneklenmiş versiyonunun spektrumundaki düşük frekanslı bir bileşenin kimliğini alan, bir sinyalin spektrumundaki yüksek frekanslı bir bileşen olgusu" olarak adlandırılabilir.
Takma adın etkisini azaltmak için alınan düzeltici önlemler şunlardır:
PCM'nin verici bölümünde bir low pass anti-aliasing filter istenmeyen yüksek frekans bileşenlerini ortadan kaldırmak için örnekleyiciden önce kullanılır.
Filtrelemeden sonra örneklenen sinyal, Nyquist oranından biraz daha yüksek bir hızda örneklenir.
Nyquist oranından daha yüksek örnekleme oranına sahip olma seçeneği, aynı zamanda daha kolay tasarımına da yardımcı olur. reconstruction filter alıcıda.
Fourier Dönüşümünün Kapsamı
Genel olarak, sinyallerin analizinde ve ayrıca teoremlerin ispatlanmasında Fourier serileri ve Fourier dönüşümlerinden yardım aradığımız görülmektedir. Çünkü -
Fourier Dönüşümü, periyodik olmayan sinyaller için Fourier serisinin uzantısıdır.
Fourier dönüşümü, sinyalleri farklı alanlarda görüntülemeye yardımcı olan ve sinyalleri kolayca analiz etmeye yardımcı olan güçlü bir matematiksel araçtır.
Bu Fourier dönüşümü kullanılarak herhangi bir sinyal sinüs ve kosinüs toplamı cinsinden ayrıştırılabilir.
Bir sonraki bölümde, Niceleme kavramı hakkında tartışalım.
Analog sinyallerin sayısallaştırılması, analog değerlere yaklaşık olarak eşit olan değerlerin yuvarlanmasını içerir. Örnekleme yöntemi, analog sinyal üzerinde birkaç nokta seçer ve daha sonra bu noktalar, değeri neredeyse stabilize bir değere yuvarlamak için birleştirilir. Böyle bir süreç şöyle adlandırılırQuantization.
Analog Sinyali Niceleme
Analogdan dijitale dönüştürücüler, verilen analog sinyalden bir dizi dijital değer oluşturmak için bu tür bir işlevi gerçekleştirir. Aşağıdaki şekil bir analog sinyali temsil etmektedir. Bu sinyalin dijitale dönüştürülmesi için örnekleme ve niceleme işleminden geçmesi gerekir.
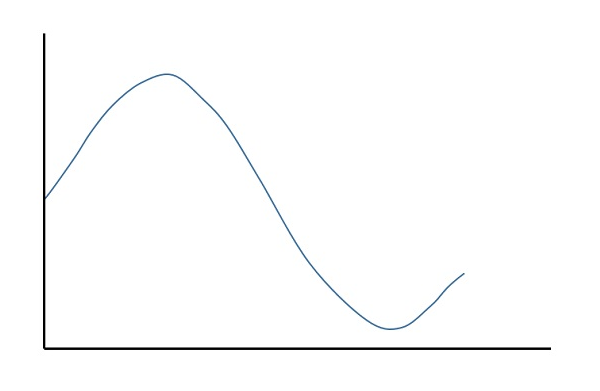
Bir analog sinyalin nicelendirilmesi, sinyalin birkaç niceleme seviyesi ile ayrıştırılmasıyla yapılır. Quantization amplitüdün örneklenmiş değerlerini sonlu bir seviye seti ile temsil eder, bu da sürekli genlikli bir örneği ayrı bir zaman sinyaline dönüştürmek anlamına gelir.
Aşağıdaki şekil bir analog sinyalin nasıl nicelleştirildiğini gösterir. Mavi çizgi analog sinyali temsil ederken, kahverengi çizgi nicelenmiş sinyali temsil eder.
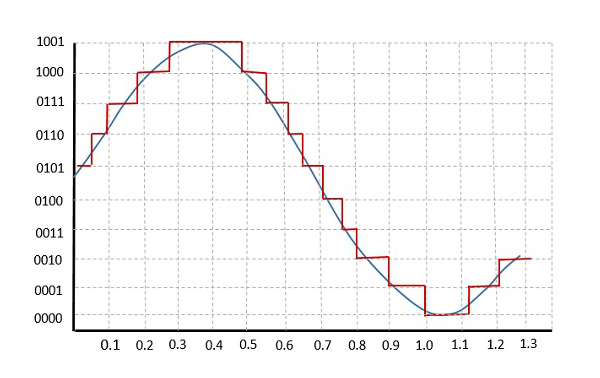
Hem örnekleme hem de niceleme bilgi kaybına neden olur. Bir Quantizer çıktısının kalitesi, kullanılan niceleme seviyelerinin sayısına bağlıdır. Nicelenmiş çıktının ayrık genlikleri şöyle adlandırılırrepresentation levels veya reconstruction levels. İki bitişik temsil düzeyi arasındaki boşluğa birquantum veya step-size.
Aşağıdaki şekil, verilen analog sinyal için dijital biçim olan sonuçta ortaya çıkan nicelleştirilmiş sinyali göstermektedir.
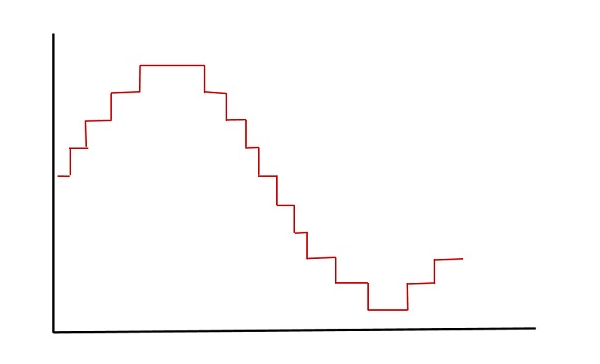
Bu aynı zamanda Stair-case dalga formu, şekline uygun olarak.
Niceleme Türleri
İki tür Niceleme vardır - Düzgün Niceleme ve Düzgün Olmayan Niceleme.
Niceleme seviyelerinin eşit aralıklarla yerleştirildiği niceleme türü, Uniform Quantization. Niceleme seviyelerinin eşit olmadığı ve çoğunlukla aralarındaki ilişkinin logaritmik olduğu niceleme türü,Non-uniform Quantization.
İki tür tek tip niceleme vardır. Mid-Rise tipi ve Mid-Tread tipidir. Aşağıdaki şekiller, iki tip tekdüze nicemlemeyi temsil etmektedir.
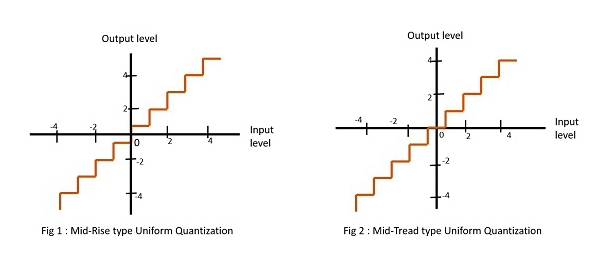
Şekil 1, orta yükselmeli tipi göstermektedir ve Şekil 2, tek tip nicemlemenin orta dişli tipini göstermektedir.
Mid-Risetip denir çünkü başlangıç noktası merdiven kasası benzeri grafiğin yükselen kısmının ortasında yer alır. Bu türdeki niceleme seviyeleri sayıca çifttir.
Mid-treadtip denir çünkü başlangıç noktası merdiven kasası benzeri grafiğin bir basamağının ortasında yer alır. Bu türdeki niceleme seviyeleri tek sayıdır.
Hem orta yükselmeli hem de orta dişli tipteki tek tip niceleyiciler, orijine göre simetriktir.
Niceleme Hatası
Herhangi bir sistem için, işleyişi sırasında, giriş ve çıkış değerlerinde her zaman bir fark vardır. Sistemin işlenmesi, bu değerlerin farkı olan bir hatayla sonuçlanır.
Bir girdi değeri ile nicelleştirilmiş değeri arasındaki farka Quantization Error. BirQuantizerNiceleme (değeri yuvarlayarak) gerçekleştiren logaritmik bir işlevdir. Analogdan dijitale dönüştürücü (ADC) bir niceleyici olarak çalışır.
Aşağıdaki şekil, orijinal sinyal ile nicelenmiş sinyal arasındaki farkı gösteren bir niceleme hatası için bir örnek göstermektedir.
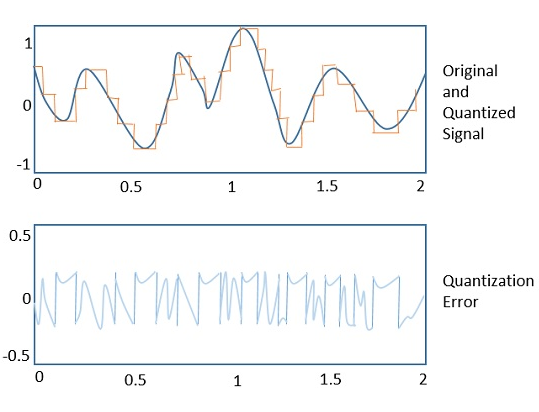
Niceleme Gürültüsü
Genellikle analog ses sinyalinde onu dijitale nicelendirirken ortaya çıkan bir tür niceleme hatasıdır. Örneğin müzikte, hatalarda bir düzenlilik bulunmadığı yerlerde sinyaller sürekli değişiyor. Bu tür hatalar,Quantization Noise.
PCM'de genişleme
Kelime CompandingSıkıştırma ve Genişletmenin bir kombinasyonudur, yani her ikisini de yapar. Bu, vericideki verileri sıkıştıran ve alıcıda aynı verileri genişleten PCM'de kullanılan doğrusal olmayan bir tekniktir. Bu teknik kullanılarak gürültü ve parazitin etkileri azaltılır.
İki tür Companding tekniği vardır. Onlar -
A-kanunu Zorlama Tekniği
Üniform niceleme elde edilir A = 1karakteristik eğri doğrusaldır ve sıkıştırma yapılmaz.
A-kanunun başlangıç noktasında orta yükselişi vardır. Dolayısıyla, sıfır olmayan bir değer içerir.
PCM telefon sistemleri için A-kanunu kompanlaması kullanılır.
µ-yasası Zorlama Tekniği
Üniform niceleme elde edilir µ = 0karakteristik eğri doğrusaldır ve sıkıştırma yapılmaz.
µ-kuralı başlangıçta orta dişe sahiptir. Dolayısıyla sıfır değeri içerir.
µ-kuralı sıkıştırma, konuşma ve müzik sinyalleri için kullanılır.
µ-law, Kuzey Amerika ve Japonya'da kullanılmaktadır.
Yüksek korelasyonlu örnekler için, PCM tekniği ile kodlandığında, gereksiz bilgileri geride bırakın. Bu fazlalık bilgiyi işlemek ve daha iyi bir çıktı elde etmek için, bir önceki çıktısından varsayılan bir tahmini örneklenmiş değer almak ve bunları nicelenmiş değerlerle özetlemek akıllıca bir karardır. Böyle bir süreç şöyle adlandırılırDifferential PCM (DPCM) tekniği.
DPCM Verici
DPCM Vericisi, iki yaz devresine sahip Quantizer ve Predictor'dan oluşur. DPCM vericisinin blok şeması aşağıdadır.

Her noktadaki sinyaller şu şekilde adlandırılır -
$ x (nT_s) $ örneklenmiş girdidir
$ \ widehat {x} (nT_s) $ öngörülen örnektir
$ e (nT_s) $, örneklenen girdi ile tahmin edilen çıktının farkıdır ve genellikle tahmin hatası olarak adlandırılır
$ v (nT_s) $ nicelleştirilmiş çıktıdır
$ u (nT_s) $, tahminci çıktısının ve niceleyici çıktısının gerçekte yaz çıktısı olan tahmin girdisidir
Öngörücü, verici devresinin önceki çıkışlarından varsayılan örnekleri üretir. Bu tahmin edicinin girdisi, $ x (nT_s) $ girdi sinyalinin nicelenmiş versiyonlarıdır.
Quantizer Çıkışı şu şekilde temsil edilir:
$$ v (nT_s) = Q [e (nT_s)] $$
$ = e (nT_s) + q (nT_s) $
Nerede q (nTs) niceleme hatası
Öngörücü girdisi, niceleyici çıktısı ile öngörü çıktısının toplamıdır,
$$ u (nT_s) = \ widehat {x} (nT_s) + v (nT_s) $$
$ u (nT_s) = \ widehat {x} (nT_s) + e (nT_s) + q (nT_s) $
$$ u (nT_s) = x (nT_s) + q (nT_s) $$
Orijinal girişi yeniden yapılandırmak için kod çözücüde aynı tahmin devresi kullanılır.
DPCM Alıcısı
DPCM Alıcısının blok diyagramı bir kod çözücü, bir tahminci ve bir yaz devresinden oluşur. DPCM Alıcısının diyagramı aşağıdadır.

Sinyallerin gösterimi öncekilerle aynıdır. Gürültünün olmadığı durumlarda, kodlanmış alıcı girişi, kodlanmış verici çıkışı ile aynı olacaktır.
Daha önce bahsedildiği gibi, tahminci, önceki çıktılara dayalı olarak bir değer varsayar. Kod çözücüye verilen girdi işlenir ve bu çıktı, daha iyi bir çıktı elde etmek için tahmin edicinin çıktısı ile toplanır.
Daha iyi örnekleme elde etmek için bir sinyalin örnekleme oranı Nyquist oranından daha yüksek olmalıdır. Diferansiyel PCM'deki bu örnekleme aralığı önemli ölçüde azaltılırsa, örneklemden örneğe genlik farkı çok küçüktür, sanki fark1-bit quantization, adım boyutu çok küçük olacaktır, yani Δ (delta).
Delta Modülasyonu
Örnekleme oranının çok daha yüksek olduğu ve nicelemeden sonraki adım boyutunun daha küçük bir değere sahip olduğu modülasyon türü Δböyle bir modülasyon şöyle adlandırılır delta modulation.
Delta Modülasyonunun Özellikleri
Aşağıda, delta modülasyonunun bazı özellikleri verilmiştir.
Sinyal korelasyonundan tam olarak yararlanmak için aşırı örneklenmiş bir giriş alınır.
Niceleme tasarımı basittir.
Giriş dizisi Nyquist oranından çok daha yüksektir.
Kalite ılımlı.
Modülatörün ve demodülatörün tasarımı basittir.
Çıkış dalga formunun merdiven durumu yaklaşımı.
Adım boyutu çok küçük, yani Δ (delta).
Bit hızına kullanıcı tarafından karar verilebilir.
Bu, daha basit uygulamayı içerir.
Delta Modülasyonu, DPCM tekniğinin basitleştirilmiş bir biçimidir ve aynı zamanda 1-bit DPCM scheme. Örnekleme aralığı kısaldıkça, sinyal korelasyonu daha yüksek olacaktır.
Delta Modülatör
Delta Modülatör, 1 bitlik bir niceleyici ve bir gecikme devresinin yanı sıra iki yaz devresinden oluşur. Aşağıda bir delta modülatörünün blok diyagramı verilmiştir.
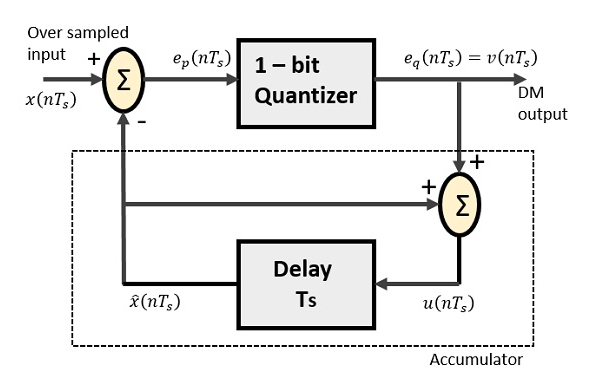
DPCM'deki tahmin devresi, DM'deki basit bir gecikme devresi ile değiştirilir.
Yukarıdaki diyagramdan şu şekilde gösterimlerimiz var:
$ x (nT_s) $ = örneklenmiş girdinin üzerinde
$ e_p (nT_s) $ = yaz çıkışı ve niceleyici girişi
$ e_q (nT_s) $ = niceleyici çıkışı = $ v (nT_s) $
$ \ widehat {x} (nT_s) $ = gecikme devresinin çıkışı
$ u (nT_s) $ = gecikme devresi girişi
Bu gösterimleri kullanarak, şimdi delta modülasyon sürecini anlamaya çalışacağız.
$ e_p (nT_s) = x (nT_s) - \ widehat {x} (nT_s) $
--------- denklem 1
$ = x (nT_s) - u ([n - 1] T_s) $
$ = x (nT_s) - [\ widehat {x} [[n - 1] T_s] + v [[n-1] T_s]] $
--------- denklem 2
Daha ileri,
$ v (nT_s) = e_q (nT_s) = S.sig. [e_p (nT_s)] $
--------- denklem 3
$ u (nT_s) = \ widehat {x} (nT_s) + e_q (nT_s) $
Nerede,
$ \ widehat {x} (nT_s) $ = gecikme devresinin önceki değeri
$ e_q (nT_s) $ = niceleyici çıkışı = $ v (nT_s) $
Bu nedenle
$ u (nT_s) = u ([n-1] T_s) + v (nT_s) $
--------- denklem 4
Bunun anlamı,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
Birikimin sıfır koşulunu varsayarak,
$ u (nT_s) = S \ displaystyle \ sum \ limits_ {j = 1} ^ n sig [e_p (jT_s)] $
Accumulated version of DM output = $ \ displaystyle \ sum \ limits_ {j = 1} ^ nv (jT_s) $
--------- denklem 5
Şimdi, şunu unutmayın
$ \ widehat {x} (nT_s) = u ([n-1] T_s) $
$ = \ displaystyle \ toplam \ limitler_ {j = 1} ^ {n - 1} v (jT_s) $
--------- denklem 6
Gecikme birimi çıkışı, bir örnek gecikmeli bir Akümülatör çıktısıdır.
5 ve 6 denklemlerinden, demodülatör için olası bir yapı elde ederiz.
Merdiven durumuna yakın bir dalga formu, delta modülatörünün adım boyutu delta (Δ). Dalga biçiminin çıktı kalitesi orta düzeydedir.
Delta Demodülatör
Delta demodülatör, bir alçak geçiren filtre, bir yaz ve bir gecikme devresinden oluşur. Öngörü devresi burada elimine edilir ve dolayısıyla demodülatöre varsayılan girdi verilmez.
Delta demodülatörünün diyagramı aşağıdadır.
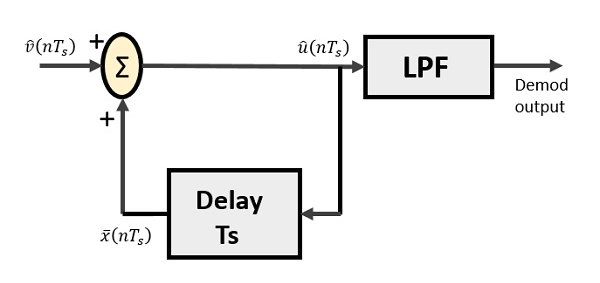
Yukarıdaki diyagramdan şu şekilde gösterimlerimiz var:
$ \ widehat {v} (nT_s) $ girdi örneğidir
$ \ widehat {u} (nT_s) $ yaz çıktısıdır
$ \ bar {x} (nT_s) $ gecikmeli çıktıdır
Demodülatöre girdi olarak bir ikili dizi verilecektir. Merdiven boşluğuna yaklaştırılmış çıktı LPF'ye verilir.
Alçak geçiren filtre birçok nedenden dolayı kullanılır, ancak bunun başlıca nedeni bant dışı sinyaller için gürültü gidermedir. Vericide meydana gelebilecek adım boyutu hatası denirgranular noise, burada elimine edilir. Gürültü yoksa, modülatör çıkışı demodülatör girişine eşittir.
DM'nin DPCM'ye Göre Avantajları
1 bitlik niceleyici
Modülatör ve demodülatörün çok kolay tasarımı
Bununla birlikte, DM'de bir miktar gürültü var.
Eğim Aşırı yük bozulması (ne zaman Δ küçük)
Granüler gürültü (ne zaman Δ büyük)
Uyarlanabilir Delta Modülasyonu (ADM)
Dijital modülasyonda, çıktı dalgasının kalitesini etkileyen belirli adım boyutunu belirleme problemiyle karşılaştık.
Modülasyon sinyalinin dik eğiminde daha büyük bir adım boyutu gereklidir ve mesajın küçük bir eğime sahip olduğu durumlarda daha küçük bir adım boyutu gereklidir. Süreçte dakika detayları gözden kaçar. Bu nedenle, örneklemeyi istenen şekilde elde etmek için ihtiyacımıza göre adım boyutunun ayarlanmasını kontrol edebilirsek daha iyi olur. Bu kavramıAdaptive Delta Modulation.
Uyarlanabilir delta modülatörünün blok şeması aşağıdadır.
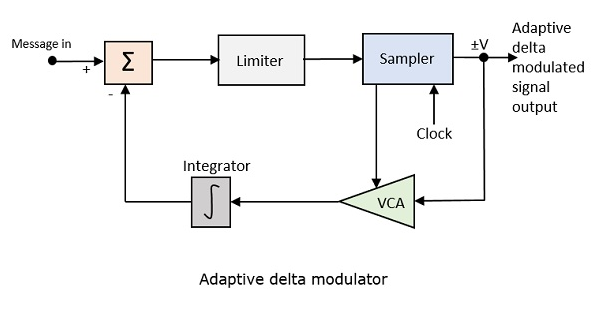
Voltaj kontrollü amplifikatörün kazancı, örnekleyiciden gelen çıkış sinyali ile ayarlanır. Amplifikatör kazancı, adım boyutunu belirler ve her ikisi de orantılıdır.
ADM, mevcut numunenin değeri ile bir sonraki numunenin tahmin edilen değeri arasındaki farkı nicelleştirir. Hızlı değişen değerlerin aslına uygun şekilde yeniden üretimi için sonraki değerleri tahmin etmek için değişken bir adım yüksekliği kullanır.
Dijital iletişim süreçlerine giden temel yolu açan birkaç teknik vardır. Sinyallerin sayısallaştırılması için örnekleme ve niceleme tekniklerine sahibiz.
Matematiksel olarak temsil edilebilmeleri için LPC ve dijital çoklama tekniklerimiz var. Bu dijital modülasyon teknikleri ayrıca tartışılmaktadır.
Doğrusal Öngörülü Kodlama
Linear Predictive Coding (LPC)doğrusal tahmin modelinde dijital konuşma sinyallerini temsil eden bir araçtır. Bu çoğunlukla ses sinyali işlemede, konuşma sentezinde, konuşma tanımada vb. Kullanılır.
Doğrusal tahmin, mevcut örneğin geçmiş örneklerin doğrusal kombinasyonuna dayandığı fikrine dayanır. Analiz, önceki örneklerin doğrusal bir fonksiyonu olarak bir ayrık zaman sinyalinin değerlerini tahmin eder.
Spektral zarf, doğrusal tahmin modelinin bilgileri kullanılarak sıkıştırılmış bir biçimde temsil edilir. Bu matematiksel olarak şu şekilde temsil edilebilir:
$ s (n) = \ displaystyle \ sum \ limits_ {k = 1} ^ p \ alpha_k s (n - k) $ 'ın bir değeri için p ve αk
Nerede
s(n) güncel konuşma örneğidir
k belirli bir örnektir
p en yeni değer
αk yordayıcı ortak verimli mi
s(n - k) önceki konuşma örneğidir
LPC için, öngörücü ortak-verimli değerleri, gerçek konuşma örnekleri ile doğrusal olarak tahmin edilenler arasındaki kare farkların toplamının (sonlu bir aralıkta) en aza indirilmesiyle belirlenir.
Bu çok kullanışlı bir yöntemdir encoding speechdüşük bit hızında. LPC yöntemi,Fast Fourier Transform (FFT) yöntem.
Çoğullama
Multiplexingbirden fazla sinyali ortak bir ortam üzerinden tek bir sinyalde birleştirme işlemidir. Bu sinyaller, doğası gereği analog ise, süreç şu şekilde adlandırılır:analog multiplexing. Dijital sinyaller çoklanmışsa, bunadigital multiplexing.
Çoğullama ilk olarak telefonda geliştirildi. Tek bir kablo üzerinden göndermek için bir dizi sinyal birleştirildi. Çoklama işlemi, bir iletişim kanalını birkaç mantıksal kanala böler, her birini farklı bir mesaj sinyali veya aktarılacak bir veri akışı için tahsis eder. Çoklama yapan cihaz, birMUX. Alıcıda yapılan ters işlem, yani birden fazla kanalın çıkarılması işleminede-multiplexing. Çoğullama çözen cihazaDEMUX.
Aşağıdaki şekiller MUX ve DEMUX'u temsil etmektedir. Birincil kullanımları iletişim alanındadır.
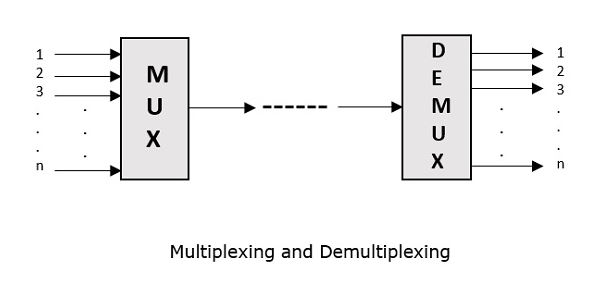
Çoklayıcı Türleri
Analog ve dijital olmak üzere başlıca iki tür çoklayıcı vardır. Ayrıca FDM, WDM ve TDM olarak ayrılırlar. Aşağıdaki şekil bu sınıflandırma hakkında ayrıntılı bir fikir vermektedir.
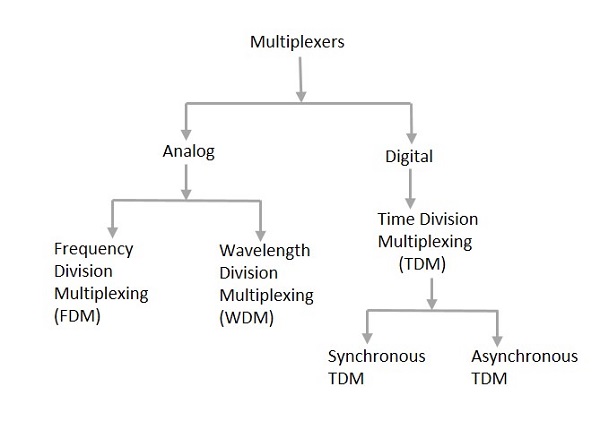
Aslında, birçok çeşit çoğullama tekniği vardır. Hepsinden, yukarıdaki şekilde belirtilen genel sınıflandırmaya sahip ana türlere sahibiz.
Analog Çoklama
Analog çoklama teknikleri, doğası gereği analog olan sinyalleri içerir. Analog sinyaller, frekanslarına (FDM) veya dalga boylarına (WDM) göre çoklanır.
Frekans Bölmeli Çoğullama (FDM)
Analog çoklamada en çok kullanılan teknik Frequency Division Multiplexing (FDM). Bu teknik, veri akışlarını tek bir sinyal olarak bir iletişim ortamında göndermek üzere birleştirmek için çeşitli frekanslar kullanır.
Example - Tek bir kablo üzerinden bir dizi kanalı gönderen geleneksel bir televizyon vericisi FDM kullanır.
Dalgaboyu Bölmeli Çoğullama (WDM)
Dalgaboyu Bölmeli çoğullama, ışık spektrumunda farklı dalga boylarındaki birçok veri akışının iletildiği analog bir tekniktir. Dalgaboyu artarsa, sinyalin frekansı azalır. Birprism Farklı dalga boylarını tek bir hatta çevirebilen MUX çıkışı ve DEMUX girişinde kullanılabilir.
Example - Optik fiber iletişim, farklı dalga boylarını iletişim için tek bir ışıkta birleştirmek için WDM tekniğini kullanır.
Dijital Çoklama
Dijital terimi, ayrık bilgi bitlerini temsil eder. Dolayısıyla, mevcut veriler, ayrık çerçeveler veya paketler şeklindedir.
Zaman Bölmeli Çoğullama (TDM)
TDM'de, zaman çerçevesi aralıklara bölünmüştür. Bu teknik, her mesaj için bir dilim tahsis ederek tek bir iletişim kanalı üzerinden bir sinyal iletmek için kullanılır.
Tüm TDM türlerinden ana olanlar Senkron ve Asenkron TDM'dir.
Senkron TDM
Senkron TDM'de, giriş bir çerçeveye bağlanır. Eğer varsa 'n"bağlantı sayısı, ardından çerçeve bölünür"n' zaman dilimleri. Her giriş satırı için bir yuva tahsis edilmiştir.
Bu teknikte, örnekleme oranı tüm sinyaller için ortaktır ve bu nedenle aynı saat girişi verilir. MUX, her zaman her cihaza aynı yuvayı tahsis eder.
Eşzamansız TDM
Eşzamansız TDM'de, örnekleme hızı her sinyal için farklıdır ve ortak bir saat gerekli değildir. Tahsis edilen cihaz, bir zaman aralığı için hiçbir şey iletmez ve boşta kalırsa, bu yuva senkronizasyonun aksine başka bir cihaza tahsis edilir. Bu tür TDM, Eşzamansız aktarım modu ağlarında kullanılır.
Rejeneratif Tekrarlayıcı
Herhangi bir iletişim sisteminin güvenilir olabilmesi için sinyalleri etkin bir şekilde kayıpsız iletmesi ve alması gerekir. Bir PCM dalgası, bir kanaldan iletildikten sonra, kanalın getirdiği gürültü nedeniyle bozulur.
Orijinal ve alınan darbe ile karşılaştırıldığında rejeneratif darbe aşağıdaki şekilde gösterildiği gibi olacaktır.

Sinyalin daha iyi bir şekilde yeniden üretilmesi için devre olarak adlandırılan bir devre regenerative repeateralıcıdan önceki yolda kullanılır. Bu, meydana gelen kayıplardan sinyallerin geri yüklenmesine yardımcı olur. Şematik gösterim aşağıdadır.
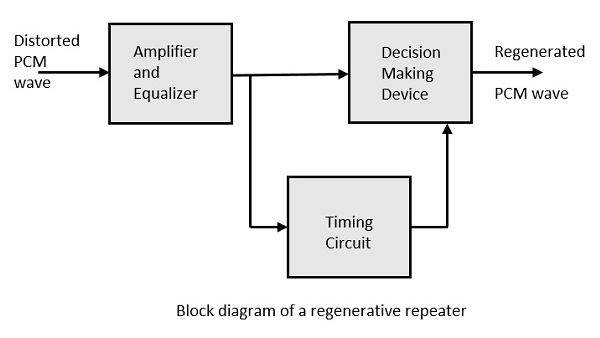
Bu, bir amplifikatör, bir zamanlama devresi ve bir karar verme cihazıyla birlikte bir ekolayzırdan oluşur. Bileşenlerin her birinin çalışması aşağıdaki şekilde detaylandırılmıştır.
Ekolayzer
Kanal, sinyallere genlik ve faz bozulmaları üretir. Bu, kanalın iletim özelliklerinden kaynaklanmaktadır. Ekolayzer devresi, alınan darbeleri şekillendirerek bu kayıpları telafi eder.
Zamanlama Devresi
Kaliteli bir çıktı elde etmek için, sinyallerin örneklenmesi sinyal-gürültü oranının (SNR) maksimum olduğu yerde yapılmalıdır. Bu mükemmel örneklemeyi başarmak için, zamanlama devresi tarafından yapılan alınan darbelerden periyodik bir darbe dizisi türetilmelidir.
Bu nedenle, zamanlama devresi, alınan darbeler aracılığıyla yüksek SNR'de örnekleme için zamanlama aralığını tahsis eder.
Karar Cihazı
Zamanlama devresi örnekleme zamanlarını belirler. Karar cihazı bu örnekleme zamanlarında etkinleştirilir. Karar cihazı, çıktısını, nicelenmiş darbenin ve gürültünün genliğinin önceden belirlenmiş bir değeri aşıp aşmadığına göre karar verir.
Bunlar, dijital iletişimde kullanılan tekniklerden birkaçıdır. Veri kodlama teknikleri olarak adlandırılan öğrenilmesi gereken başka önemli teknikler de vardır. Satır kodlarına bir göz attıktan sonra sonraki bölümlerde bunları öğrenelim.
Bir line codebir dijital sinyalin bir iletim hattı üzerinden veri iletimi için kullanılan koddur. Bu kodlama işlemi, semboller arası girişim gibi üst üste gelme ve sinyal bozulmasını önleyecek şekilde seçilir.
Çizgi Kodlamanın Özellikleri
Aşağıda satır kodlamasının özellikleri verilmiştir -
Tek bir sinyal üzerinde daha fazla bitin iletilmesini sağlamak için kodlama yapıldığından, kullanılan bant genişliği çok azalır.
Belirli bir bant genişliği için güç verimli bir şekilde kullanılır.
Hata olasılığı çok azalmıştır.
Hata tespiti yapılır ve bipolar da düzeltme kabiliyetine sahiptir.
Güç yoğunluğu çok uygundur.
Zamanlama içeriği yeterlidir.
Uzun dizeler 1s ve 0s şeffaflığı korumaktan kaçınılır.
Çizgi Kodlama Türleri
3 tür Hat Kodlaması vardır
- Unipolar
- Polar
- Bi-polar
Tek Kutuplu Sinyalleşme
Tek kutuplu sinyalleşme olarak da adlandırılır On-Off Keying ya da sadece OOK.
Nabzın varlığı bir 1 ve nabzın yokluğu bir 0.
Unipolar sinyallemede iki varyasyon vardır -
- Sıfıra Dönmez (NRZ)
- Sıfıra Dön (RZ)
Tek Kutuplu Sıfıra Dönmeyen (NRZ)
Bu tip tek kutuplu sinyallemede, yüksek veri olarak adlandırılan pozitif bir darbe ile temsil edilir. Marksüresi olan T0sembol bit süresine eşittir. Düşük veri girişinde darbe yok.
Aşağıdaki şekil bunu açıkça göstermektedir.
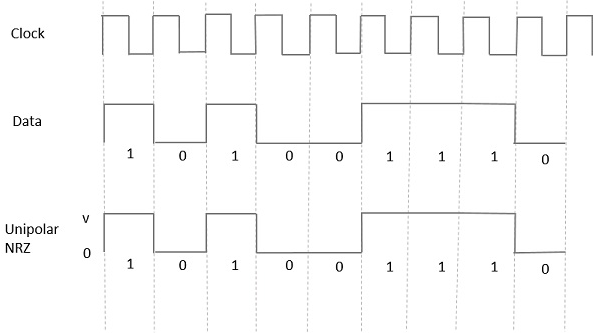
Advantages
Unipolar NRZ'nin avantajları şunlardır:
- Basit.
- Daha az bant genişliği gereklidir.
Disadvantages
Unipolar NRZ'nin dezavantajları şunlardır:
Hata düzeltmesi yapılmadı.
Düşük frekans bileşenlerinin varlığı sinyalin düşmesine neden olabilir.
Saat yok.
Senkronizasyon kaybı meydana gelebilir (özellikle uzun dizeler için 1s ve 0s).
Tek Kutuplu Sıfıra Dönüş (RZ)
Bu tip tek kutuplu sinyallemede, yüksek veri, ancak bir Mark pulse, süresi T0sembol bit süresinden daha az. Bit süresinin yarısı yüksek kalır, ancak hemen sıfıra döner ve bit süresinin kalan yarısı boyunca darbenin olmadığını gösterir.
Aşağıdaki şekil yardımı ile açıkça anlaşılmaktadır.
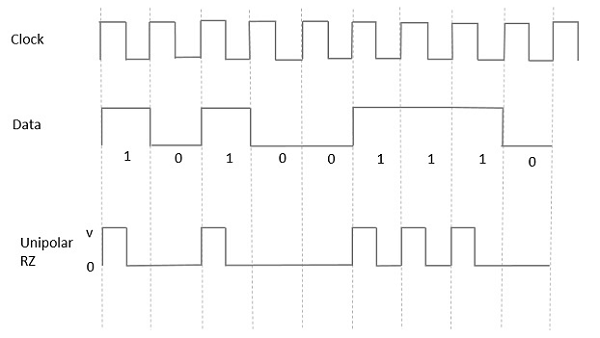
Advantages
Unipolar RZ'nin avantajları şunlardır:
- Basit.
- Sembol hızında bulunan spektral çizgi saat olarak kullanılabilir.
Disadvantages
Unipolar RZ'nin dezavantajları şunlardır:
- Hata düzeltmesi yok.
- Tek kutuplu NRZ'ye göre iki kat daha fazla bant genişliği kaplar.
- 0 Hz'de sinyalin sıfır olmadığı yerlerde sinyal düşüşüne neden olur.
Kutupsal Sinyalleşme
Polar Sinyallemenin iki yöntemi vardır. Onlar -
- Polar NRZ
- Polar RZ
Polar NRZ
Bu tür Polar sinyallemede, bir Yüksek veri pozitif bir darbe ile temsil edilirken, bir Düşük veri negatif bir darbe ile temsil edilir. Aşağıdaki şekil bunu iyi gösteriyor.
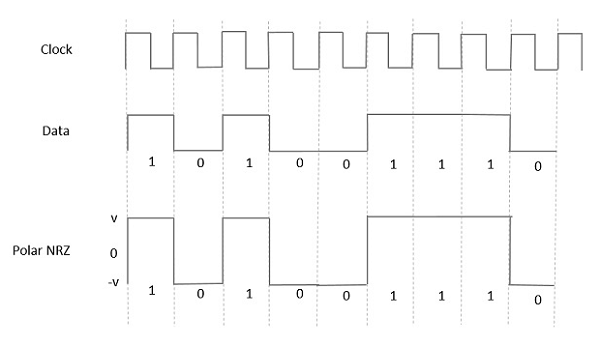
Advantages
Polar NRZ'nin avantajları şunlardır:
- Basit.
- Düşük frekanslı bileşen yoktur.
Disadvantages
Polar NRZ'nin dezavantajları -
Hata düzeltmesi yok.
Saat yok.
Sinyal düşüşüne, sinyalin sıfır olmayan yerlerde neden olur. 0 Hz.
Polar RZ
Bu tür Polar sinyallemede, bir Yüksek veri, ancak bir Mark pulse, süresi T0sembol bit süresinden daha az. Bit süresinin yarısı yüksek kalır, ancak hemen sıfıra döner ve bit süresinin kalan yarısı boyunca darbenin olmadığını gösterir.
Bununla birlikte, Düşük bir giriş için, negatif bir darbe veriyi temsil eder ve sıfır seviyesi bit süresinin diğer yarısı için aynı kalır. Aşağıdaki şekil bunu açıkça göstermektedir.
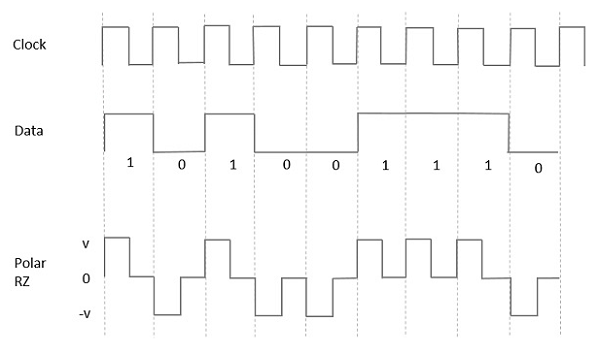
Advantages
Polar RZ'nin avantajları şunlardır:
- Basit.
- Düşük frekanslı bileşen yoktur.
Disadvantages
Polar RZ'nin dezavantajları -
Hata düzeltmesi yok.
Saat yok.
Polar NRZ'nin iki katı bant genişliğini kaplar.
Sinyal düşüşü, sinyalin sıfır olmadığı yerlerde meydana gelir. 0 Hz.
Bipolar Sinyalleşme
Bu, üç voltaj seviyesine sahip bir kodlama tekniğidir. +, - ve 0. Böyle bir sinyale şöyle denirduo-binary signal.
Bu türün bir örneği Alternate Mark Inversion (AMI). Bir1, voltaj seviyesi alternatif olarak + ila - veya - ila + arasında bir geçiş alır. 1seşit kutupluluğa sahip olmak. Bir0 sıfır voltaj seviyesine sahip olacaktır.
Bu yöntemde bile iki tipimiz var.
- Bipolar NRZ
- Bipolar RZ
Şimdiye kadar tartışılan modellerden NRZ ve RZ arasındaki farkı öğrendik. Burada da aynı şekilde gidiyor. Aşağıdaki şekil bunu açıkça göstermektedir.
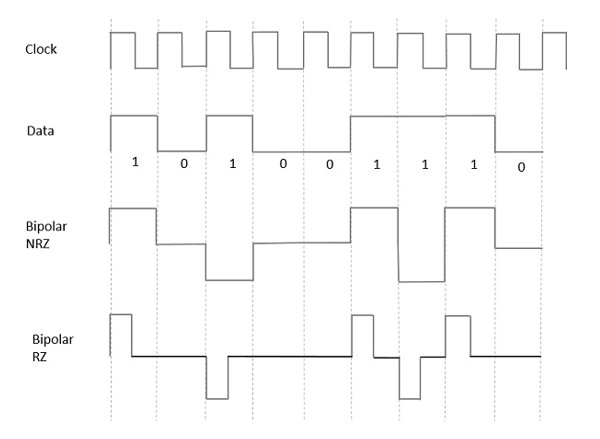
Yukarıdaki şekil hem Bipolar NRZ hem de RZ dalga formlarına sahiptir. Darbe süresi ve sembol bit süresi NRZ tipinde eşittir, darbe süresi ise RZ tipinde sembol bit süresinin yarısıdır.
Avantajlar
Avantajlar aşağıdadır -
Basit.
Düşük frekanslı bileşen yoktur.
Tek kutuplu ve kutuplu NRZ düzenlerinden daha düşük bant genişliği işgal eder.
Bu teknik, burada sinyal azalması meydana gelmediğinden AC bağlı hatlar üzerinden iletim için uygundur.
Bunda tek bir hata tespit kabiliyeti mevcuttur.
Dezavantajları
Dezavantajlar aşağıdadır -
- Saat yok.
- Uzun veri dizileri senkronizasyon kaybına neden olur.
Güç Spektral Yoğunluğu
Bir sinyalin gücünün çeşitli frekanslarda frekans alanında nasıl dağıldığını tanımlayan fonksiyona denir. Power Spectral Density (PSD).
PSD, Otomatik Korelasyonun Fourier Dönüşümüdür (Gözlemler arasındaki benzerlik). Dikdörtgen bir darbe şeklindedir.
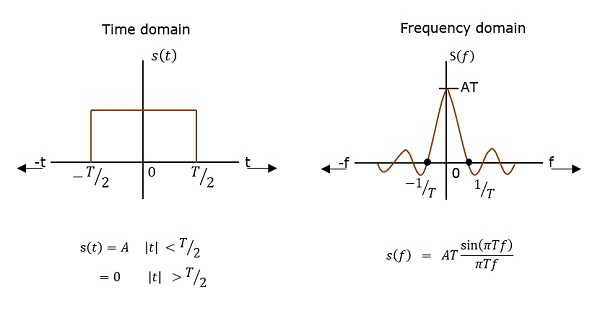
PSD Derivasyonu
Einstein-Wiener-Khintchine teoremine göre, rastgele bir sürecin oto korelasyon fonksiyonu veya güç spektral yoğunluğu biliniyorsa, diğeri tam olarak bulunabilir.
Dolayısıyla, spektral güç yoğunluğunu türetmek için, aşağıda gösterildiği gibi bir güç sinyalinin $ x (tau)) $ zaman otomatik korelasyonunu kullanacağız.
$ R_x (\ tau) = \ lim_ {T_p \ rightarrow \ infty} \ frac {1} {T_p} \ int _ {\ frac {{- T_p}} {2}} ^ {\ frac {T_p} {2}} x (t) x (t + \ tau) dt $
$ X (t) $ dürtülerden oluştuğu için, $ R_x (\ tau) $ şu şekilde yazılabilir:
$ R_x (\ tau) = \ frac {1} {T} \ displaystyle \ toplamı \ limitler_ {n = - \ infty} ^ \ infty R_n \ delta (\ tau - nT) $
$ R_n = \ lim_ {N \ rightarrow \ infty} \ frac {1} {N} \ sum_ka_ka_ {k + n} $
Gerçek sinyaller için $ R_n = R _ {- n} $ olduğunu öğreniyoruz, elimizde
$ S_x (w) = \ frac {1} {T} (R_0 + 2 \ displaystyle \ sum \ limits_ {n = 1} ^ \ infty R_n \ cos nwT) $
Darbe filtresi $ (w) \ leftrightarrow f (t) $ spektrumuna sahip olduğundan,
$ s_y (w) = \ mid F (w) \ mid ^ 2S_x (w) $
$ = \ frac {\ orta F (w) \ orta ^ 2} {T} (\ displaystyle \ toplam \ limit_ {n = - \ infty} ^ \ infty R_ne ^ {- jnwT_ {b}}) $
$ = \ frac {\ orta F (w) \ orta ^ 2} {T} (R_0 + 2 \ displaystyle \ sum \ limits_ {n = 1} ^ \ infty R_n \ cos nwT) $
Bu nedenle, Güç Spektral Yoğunluğu denklemini elde ederiz. Bunu kullanarak çeşitli hat kodlarının PSD'sini bulabiliriz.
Encoding verilerin güvenli bir şekilde iletilmesi için verinin veya belirli bir karakter, sembol, alfabe vb. dizisinin belirli bir formata dönüştürülmesi işlemidir. Decoding bilgiyi dönüştürülmüş formattan çıkarmak için ters kodlama işlemidir.
Veri Kodlama
Kodlama, temsil etmek için çeşitli voltaj veya akım seviyeleri modellerini kullanma işlemidir. 1s ve 0s iletim bağlantısındaki dijital sinyallerin
Yaygın hat kodlama türleri Unipolar, Polar, Bipolar ve Manchester'dır.
Kodlama Teknikleri
Veri kodlama tekniği, veri dönüştürme türüne bağlı olarak aşağıdaki türlere ayrılır.
Analog data to Analog signals - Analog sinyallerin Genlik Modülasyonu, Frekans Modülasyonu ve Faz Modülasyonu gibi modülasyon teknikleri bu kategoriye girer.
Analog data to Digital signals- Bu işlem, Darbe Kod Modülasyonu (PCM) ile yapılan sayısallaştırma olarak adlandırılabilir. Dolayısıyla, dijital modülasyondan başka bir şey değildir. Daha önce tartıştığımız gibi, örnekleme ve niceleme bunda önemli faktörlerdir. Delta Modülasyonu, PCM'den daha iyi bir çıktı verir.
Digital data to Analog signals- Genlik Kaydırmalı Anahtarlama (ASK), Frekans Kaymalı Anahtarlama (FSK), Faz Kaymalı Anahtarlama (PSK) vb. Gibi modülasyon teknikleri bu kategoriye girer. Bunlar sonraki bölümlerde tartışılacaktır.
Digital data to Digital signals- Bunlar bu bölümde. Dijital verileri dijital sinyallerle eşlemenin birkaç yolu vardır. Bazıları -
Sıfıra Dönmez (NRZ)
NRZ Kodları, 1 Yüksek voltaj seviyesi için ve 0Düşük voltaj seviyesi için. NRZ kodlarının ana davranışı, voltaj seviyesinin bit aralığında sabit kalmasıdır. Bir bitin sonu veya başlangıcı gösterilmez ve önceki bitin değeri ile mevcut bitin değeri aynıysa, aynı voltaj durumunu koruyacaktır.
Aşağıdaki şekil NRZ kodlama kavramını açıklamaktadır.
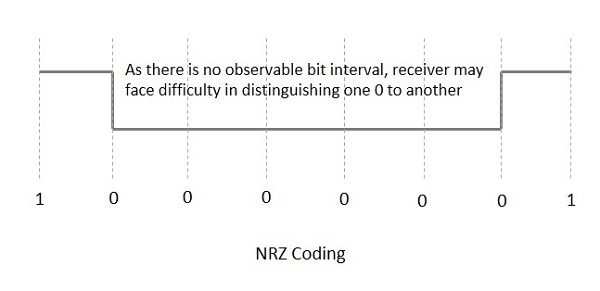
Yukarıdaki örnek dikkate alınırsa, uzun bir sabit voltaj seviyesi dizisi olduğundan ve bit aralığının olmaması nedeniyle saat senkronizasyonu kaybolabileceğinden, alıcının 0 ile 1 arasında ayrım yapması zorlaşır.
NRZ'de iki varyasyon vardır:
NRZ - L (NRZ - SEVİYE)
Yalnızca gelen sinyal 1'den 0'a veya 0'dan 1'e değiştiğinde sinyalin polaritesinde bir değişiklik olur. Bu NRZ ile aynıdır, ancak giriş sinyalinin ilk bitinde bir polarite değişikliği olmalıdır.
NRZ - I (NRZ - TERS)
Eğer bir 1gelen sinyalde oluşur, ardından bit aralığının başlangıcında bir geçiş olur. Bir0 gelen sinyalde, bit aralığının başlangıcında geçiş yoktur.
NRZ kodlarında disadvantage Verici saatinin alıcı saatiyle senkronizasyonunun, bir dizi olduğunda, tamamen bozulduğu 1s ve 0s. Bu nedenle, ayrı bir saat hattının sağlanması gerekir.
İki fazlı Kodlama
Sinyal seviyesi hem başlangıçta hem de ortada her bit zamanı için iki kez kontrol edilir. Dolayısıyla, saat hızı veri aktarım hızının iki katıdır ve bu nedenle modülasyon hızı da iki katına çıkar. Saat, sinyalin kendisinden alınır. Bu kodlama için gereken bant genişliği daha fazladır.
İki tür İki Aşamalı Kodlama vardır.
- İki aşamalı Manchester
- Diferansiyel Manchester
İki aşamalı Manchester
Bu tür kodlamada, geçiş bit aralığının ortasında yapılır. Giriş biti 1 için, aralığın ortasında ortaya çıkan darbenin geçişi Yüksek'ten Düşük'e doğrudur. Geçiş, giriş biti için Düşük'ten Yüksek'e iken0.
Diferansiyel Manchester
Bu tür kodlamada, her zaman bit aralığının ortasında bir geçiş meydana gelir. Bit aralığının başlangıcında bir geçiş meydana gelirse, giriş biti0. Bit aralığının başlangıcında geçiş olmazsa, giriş biti1.
Aşağıdaki şekil, farklı dijital girişler için NRZ-L, NRZ-I, İki-fazlı Manchester ve Diferansiyel Manchester kodlamasının dalga biçimlerini göstermektedir.
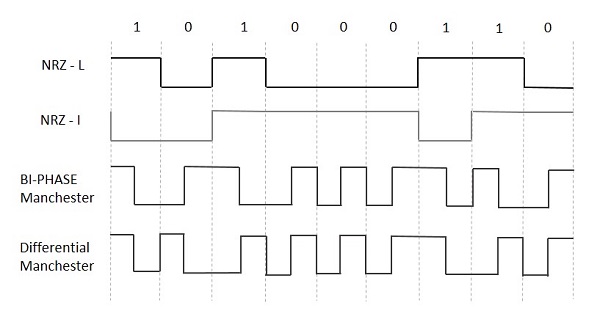
Blok Kodlama
Blok kodlama türleri arasında en ünlüleri 4B / 5B kodlama ve 8B / 6T kodlamadır. Bu işlemlerin her ikisinde de bit sayısı farklı şekillerde işlenir.
4B / 5B Kodlama
Manchester kodlamasında veriyi göndermek için NRZ kodlamasından ziyade iki kat hızlı saatler gereklidir. Burada, adından da anlaşılacağı gibi, 4 bitlik kod, minimum sayıda 5 bit ile eşlenir.1 gruptaki bitler.
NRZ-I kodlamadaki saat senkronizasyon problemi, 4 ardışık bitlik her bloğun yerine 5 bitlik eşdeğer bir kelime atanarak önlenir. Bu 5 bitlik sözcükler bir sözlükte önceden belirlenmiştir.
5 bitlik bir kod seçmenin temel fikri şudur: one leading 0 ve olmalı no more than two trailing 0s. Bu nedenle, bu kelimeler, bit bloğu başına iki işlem olacak şekilde seçilir.
8B / 6T Kodlama
Tek bir sinyal üzerinden tek bir bit göndermek için iki voltaj seviyesi kullandık. Ancak 3'ten fazla voltaj seviyesi kullanırsak, sinyal başına daha fazla bit gönderebiliriz.
Örneğin, tek bir sinyal üzerinde 8 biti temsil etmek için 6 voltaj seviyesi kullanılırsa, bu tür bir kodlama, 8B / 6T kodlama olarak adlandırılır. Dolayısıyla bu yöntemde, sinyal için 729 (3 ^ 6) kombinasyona ve bitler için 256 (2 ^ 8) kombinasyona sahibiz.
Bunlar, dijital verilerin güvenilir veri aktarımı için sıkıştırılarak veya kodlanarak dijital sinyallere dönüştürülmesinde çoğunlukla kullanılan tekniklerdir.
Farklı kodlama tekniklerinden geçtikten sonra, verilerin nasıl bozulmaya eğilimli olduğu ve güvenilir bir iletişim kurmak için etkilenmesini önlemek için nasıl önlemler alındığı hakkında bir fikrimiz var.
Oluşması en muhtemel olan başka bir önemli bozulma daha vardır. Inter-Symbol Interference (ISI).
Semboller arası girişim
Bu, bir veya daha fazla simgenin sonraki sinyallere müdahale ettiği, gürültüye neden olduğu veya zayıf bir çıktı verdiği bir sinyal bozulmasının bir biçimidir.
ISI nedenleri
ISI'nin ana nedenleri -
- Çok yollu Yayılma
- Kanallarda doğrusal olmayan frekans
ISI istenmeyen bir durumdur ve temiz bir çıktı elde etmek için tamamen ortadan kaldırılmalıdır. ISI'nin etkisini azaltmak için nedenleri de çözülmelidir.
ISI'yi alıcı çıktısında bulunan matematiksel bir biçimde görüntülemek için alıcı çıktısını dikkate alabiliriz.
Alıcı filtre çıktısı $ y (t) $, $ t_i = iT_b $ zamanında örneklenir ( i tamsayı değerleri alarak), sonuç -
$ y (t_i) = \ mu \ displaystyle \ toplam \ limitler_ {k = - \ infty} ^ {\ infty} a_kp (iT_b - kT_b) $
$ = \ mu a_i + \ mu \ displaystyle \ sum \ limits_ {k = - \ infty \\ k \ neq? i} ^ {\ infty} a_kp (iT_b - kT_b) $
Yukarıdaki denklemde, ilk terim $ \ mu a_i $, ith aktarılan bit.
İkinci terim, diğer tüm iletilen bitlerin, kod çözme üzerindeki kalıntı etkisini temsil eder. ithbit. Bu artık etki olarak adlandırılırInter Symbol Interference.
ISI yokluğunda çıktı -
$$ y (t_i) = \ mu a_i $$
Bu denklem gösteriyor ki ithiletilen bit doğru şekilde yeniden üretilir. Bununla birlikte, ISI'nin varlığı, çıktıda bit hataları ve bozulmalara neden olur.
Verici veya alıcıyı tasarlarken, çıktıyı mümkün olan en az hata oranıyla almak için ISI'nin etkilerini en aza indirmeniz önemlidir.
Bağıntılı Kodlama
Şimdiye kadar, ISI'nin istenmeyen bir fenomen olduğunu ve sinyali bozduğunu tartıştık. Ancak aynı ISI kontrollü bir şekilde kullanılırsa, bit hızına ulaşmak mümkündür.2W bant genişliği kanalında saniyedeki bit sayısı WHertz. Böyle bir şema denirCorrelative Coding veya Partial response signaling schemes.
ISI miktarı bilindiğinden, ISI'nin sinyal üzerindeki etkisinden kaçınmak için alıcıyı ihtiyaca göre tasarlamak kolaydır. Bağıntılı kodlamanın temel fikri, bir örnek dikkate alınarak elde edilir.Duo-binary Signaling.
Çift ikili Sinyalleşme
Duo-binary ismi, ikili sistemin iletim kapasitesini ikiye katlamak anlamına gelir. Bunu anlamak için bir ikili giriş dizisi düşünelim{ak} her biri bir süreye sahip olan ilişkisiz ikili rakamlardan oluşur Tasaniye. Bunda sinyal1 ile temsil edilir +1 volt ve sembol 0 tarafından -1 volt.
Bu nedenle, ikili ikili kodlayıcı çıktısı ck mevcut ikili rakamın toplamı olarak verilir ak ve önceki değer ak-1 aşağıdaki denklemde gösterildiği gibi.
$$ c_k = a_k + a_ {k-1} $$
Yukarıdaki denklem, ilişkisiz ikili dizinin giriş dizisinin {ak} ilişkili üç seviyeli darbe dizisine dönüştürülür {ck}. Darbeler arasındaki bu korelasyon, ISI'nin iletilen sinyale yapay bir şekilde dahil edilmesi olarak anlaşılabilir.
Göz Deseni
ISI'nin etkilerini incelemenin etkili bir yolu, Eye Pattern. Göz Deseni adı, ikili dalgalar için insan gözüne benzerliğinden verildi. Göz deseninin iç bölgesine denir.eye opening. Aşağıdaki şekil bir göz modelinin görüntüsünü göstermektedir.
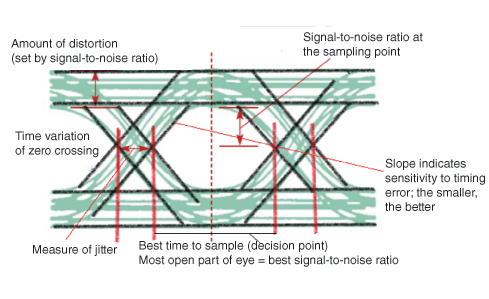
Jitter dijital sinyal anının ideal konumundan kısa vadeli değişimidir ve veri hatalarına yol açabilir.
ISI'nin etkisi arttığında göz açıklığının üst kısmından alt kısmına kadar olan izler artar ve ISI çok yüksek ise göz tamamen kapanır.
Bir göz modeli, belirli bir sistem hakkında aşağıdaki bilgileri sağlar.
Gerçek göz modelleri, bit hata oranını ve sinyal-gürültü oranını tahmin etmek için kullanılır.
Göz açıklığının genişliği, alınan dalganın ISI'den hatasız olarak örneklenebileceği zaman aralığını tanımlar.
Göz açıklığının geniş olduğu an, örnekleme için tercih edilen zaman olacaktır.
Örnekleme zamanına göre gözün kapanma oranı, sistemin zamanlama hatasına ne kadar duyarlı olduğunu belirler.
Belirli bir örnekleme zamanında göz açıklığının yüksekliği, gürültü üzerindeki marjı tanımlar.
Bu nedenle, göz modelinin yorumlanması önemli bir husustur.
Eşitleme
Güvenilir iletişimin kurulabilmesi için kaliteli bir çıktıya sahip olmamız gerekir. Kanalın iletim kayıpları ve sinyalin kalitesini etkileyen diğer faktörler tedavi edilmelidir. Bahsettiğimiz gibi, en çok meydana gelen kayıp ISI'dir.
Sinyali ISI'den arındırmak ve maksimum sinyal-gürültü oranı sağlamak için, adı verilen bir yöntem uygulamalıyız. Equalization. Aşağıdaki şekil, iletişim sisteminin alıcı kısmındaki bir ekolayzırı göstermektedir.
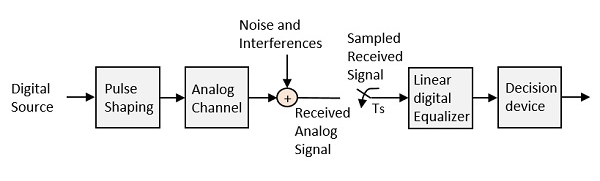
Şekilde gösterilen gürültü ve parazitlerin iletim sırasında meydana gelmesi muhtemeldir. Rejeneratif tekrarlayıcı, devreyi şekillendirerek iletim kayıplarını telafi eden bir ekolayzer devresine sahiptir. Ekolayzerin uygulanması mümkündür.
Hata Olasılığı ve Değer-değer
Verilerin iletilebildiği hız, data rate. Veri iletirken bitlerde hatanın meydana gelme oranınaBit Error Rate (BER).
BER oluşma olasılığı, Error Probability. Sinyal Gürültü Oranındaki (SNR) artış BER değerini düşürür, dolayısıyla Hata Olasılığı da azalır.
Bir Analog alıcıda, figure of merittespit sürecinde SNR çıkışının SNR girişine oranı olarak adlandırılabilir. Daha büyük bir liyakat değeri değeri bir avantaj olacaktır.
Dijitalden Analoğa sinyaller, bu bölümde tartışacağımız bir sonraki dönüşümdür. Bu tekniklere aynı zamandaDigital Modulation techniques.
Digital Modulationdaha fazla bilgi kapasitesi, yüksek veri güvenliği, mükemmel kalitede iletişim ile daha hızlı sistem kullanılabilirliği sağlar. Bu nedenle, dijital modülasyon teknikleri, analog modülasyon tekniklerinden daha büyük miktarlarda veri taşıma kapasiteleri için daha fazla talep görmektedir.
İhtiyaca bağlı olarak birçok dijital modülasyon tekniği ve bunların kombinasyonları vardır. Hepsinden öne çıkanlarını tartışacağız.
ASK - Genlik Kaydırmalı Anahtarlama
Ortaya çıkan çıktının genliği, taşıyıcı frekansına bağlı olarak sıfır seviye mi yoksa pozitif ve negatif varyasyon mu olması gerektiğine ilişkin girdi verilerine bağlıdır.
FSK - Frekans Kaydırmalı Anahtarlama
Çıkış sinyalinin frekansı, uygulanan giriş verilerine bağlı olarak yüksek veya düşük olacaktır.
PSK - Faz Kaymalı Anahtarlama
Çıkış sinyalinin fazı, girişe bağlı olarak kaydırılır. Bunlar, faz kaymalarının sayısına göre, İkili Faz Kaydırma Anahtarlama (BPSK) ve Dörtlü Faz Kaydırma Anahtarlama (QPSK) olmak üzere esas olarak iki türdendir. Diğeri, fazı önceki değere göre değiştiren Diferansiyel Faz Kaydırma Anahtarlamasıdır (DPSK).
M-ary Kodlama
Çoklu Kodlama teknikleri, ikiden fazla bitin aynı anda tek bir sinyal üzerinde iletilmesi için yapıldığı yöntemlerdir. Bu, bant genişliğinin azaltılmasına yardımcı olur.
M-ary tekniklerinin türleri:
- M-ary SOR
- M-ary FSK
- M-ary PSK
Bunların tümü sonraki bölümlerde tartışılmaktadır.
Amplitude Shift Keying (ASK) bir sinyalin genliğindeki varyasyonlar şeklinde ikili verileri temsil eden bir Genlik Modülasyonu türüdür.
Modüle edilmiş herhangi bir sinyalin yüksek frekanslı bir taşıyıcısı vardır. ASK modüle edildiğinde ikili sinyal, birzero değeri Low girdi verirken carrier output için High giriş.
Aşağıdaki şekil, girişiyle birlikte ASK modülasyonlu dalga biçimini temsil etmektedir.
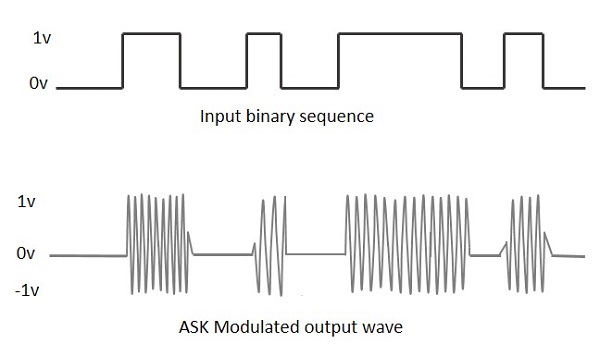
Bu ASK modülasyonlu dalgayı elde etme sürecini bulmak için ASK modülatörünün çalışmasını öğrenelim.
ASK Modülatör
ASK modülatör blok diyagramı, taşıyıcı sinyal üretecinden, mesaj sinyalinden ikili sekans ve bant sınırlı filtreden oluşur. ASK Modülatörünün blok şeması aşağıdadır.
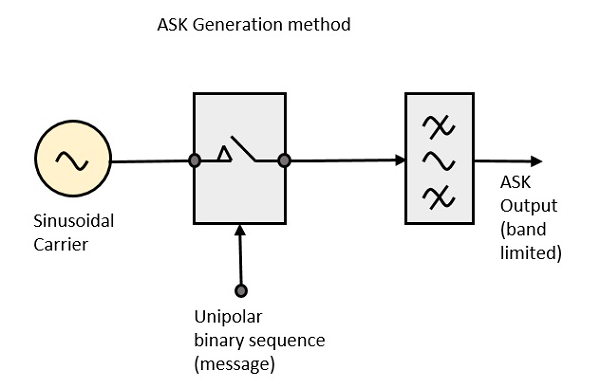
Taşıyıcı jeneratör, sürekli bir yüksek frekanslı taşıyıcı gönderir. Mesaj sinyalinden gelen ikili dizi, tek kutuplu girişin Yüksek veya Düşük olmasını sağlar. Yüksek sinyal anahtarı kapatarak bir taşıyıcı dalgaya izin verir. Dolayısıyla, çıkış, yüksek girişteki taşıyıcı sinyal olacaktır. Düşük giriş olduğunda, anahtar açılarak hiçbir voltajın görünmesine izin vermez. Bu nedenle çıktı düşük olacaktır.
Bant sınırlayıcı filtre, bant sınırlayıcı filtrenin veya darbe şekillendirme filtresinin genlik ve faz özelliklerine bağlı olarak darbeyi şekillendirir.
ASK Demodülatör
İki tür ASK Demodülasyon tekniği vardır. Onlar -
- Asenkron ASK Demodülasyonu / algılama
- Senkronize ASK Demodülasyonu / algılama
Vericideki saat frekansı, alıcıdaki saat frekansı ile eşleştiğinde, Synchronous method, frekans senkronize edildikçe. Aksi takdirde, olarak bilinirAsynchronous.
Asenkron ASK Demodülatör
Asenkron ASK detektörü, yarım dalgalı bir doğrultucu, bir alçak geçiren filtre ve bir karşılaştırıcıdan oluşur. Aşağıdakiler aynı için blok diyagramdır.
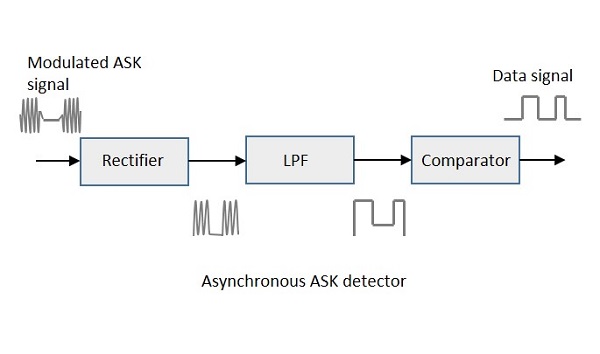
Modüle edilmiş ASK sinyali, pozitif bir yarı çıkış sağlayan yarım dalga doğrultucuya verilir. Alçak geçiren filtre, yüksek frekansları bastırır ve karşılaştırıcının dijital bir çıkış sağladığı zarf algılanan bir çıktı verir.
Senkron ASK Demodülatör
Senkronize ASK dedektörü, bir Kare yasa dedektörü, alçak geçiren filtre, bir karşılaştırıcı ve bir voltaj sınırlayıcıdan oluşur. Aşağıdakiler aynı için blok diyagramdır.
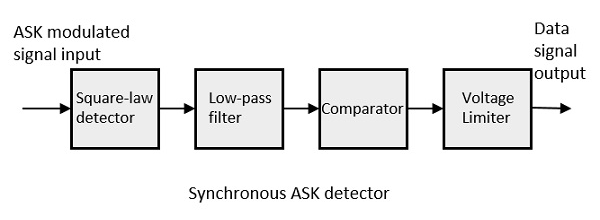
ASK modülasyonlu giriş sinyali Square law detektörüne verilir. Kare yasası detektörü, çıkış voltajı genlik modülasyonlu giriş voltajının karesiyle orantılı olan bir detektördür. Düşük geçiş filtresi, yüksek frekansları en aza indirir. Karşılaştırıcı ve voltaj sınırlayıcı, temiz bir dijital çıktı elde etmeye yardımcı olur.
Frequency Shift Keying (FSK)Taşıyıcı sinyalin frekansının dijital sinyal değişikliklerine göre değiştiği dijital modülasyon tekniğidir. FSK, bir frekans modülasyon şemasıdır.
FSK ile modüle edilmiş bir dalganın çıkışı, ikili Yüksek giriş için frekansı yüksek ve ikili Düşük giriş için frekansı düşüktür. İkili1s ve 0s Mark ve Uzay frekansları olarak adlandırılır.
Aşağıdaki görüntü, FSK ile modüle edilmiş dalga formunun girdisi ile birlikte şematik temsilidir.
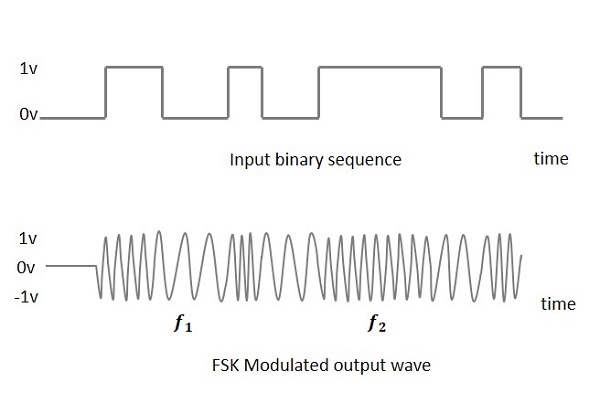
Bu FSK modülasyonlu dalgayı elde etme sürecini bulmak için, bize bir FSK modülatörünün çalışması hakkında bilgi verin.
FSK Modülatör
FSK modülatör blok diyagramı, bir saat ve giriş ikili dizisi içeren iki osilatörden oluşur. Aşağıda blok diyagramı verilmiştir.

Daha yüksek ve daha düşük frekanslı sinyaller üreten iki osilatör, dahili bir saat ile birlikte bir anahtara bağlanır. Mesajın iletimi sırasında çıkış dalga formunun ani faz süreksizliklerinden kaçınmak için, her iki osilatöre dahili olarak bir saat uygulanır. İkili giriş dizisi, ikili girişe göre frekansları seçmek için vericiye uygulanır.
FSK Demodülatör
Bir FSK dalgasını demodüle etmenin farklı yöntemleri vardır. FSK tespitinin ana yöntemleri şunlardır:asynchronous detector ve synchronous detector. Senkron detektör uyumludur, asenkron detektör ise uyumlu değildir.
Eşzamansız FSK Dedektörü
Asenkron FSK dedektörünün blok diyagramı iki bant geçiren filtre, iki zarf dedektörü ve bir karar devresinden oluşur. Aşağıdaki diyagramatik gösterimdir.
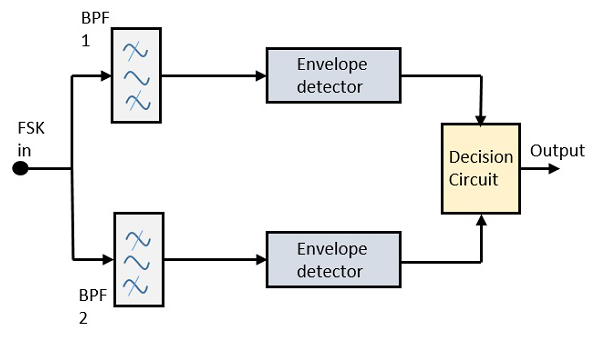
FSK sinyali, iki Bant Geçiş Filtresinden (BPF) geçirilir ve Space ve Markfrekanslar. Bu iki BPF'nin çıkışı, zarf detektörüne verilen ASK sinyaline benzer. Her zarf detektöründeki sinyal asenkron olarak modüle edilir.
Karar devresi hangi çıktının daha olası olduğunu seçer ve bunu zarf detektörlerinin herhangi birinden seçer. Ayrıca dalga biçimini dikdörtgen şeklinde yeniden şekillendirir.
Senkron FSK Dedektörü
Senkron FSK dedektörünün blok diyagramı, yerel osilatör devrelerine sahip iki karıştırıcı, iki bant geçiş filtresi ve bir karar devresinden oluşur. Aşağıdaki diyagramatik gösterimdir.
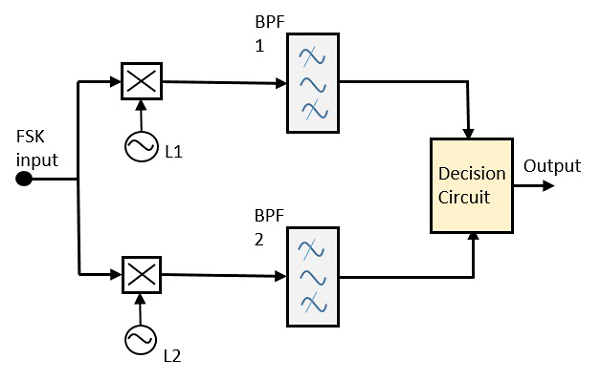
FSK sinyal girişi, yerel osilatör devrelerine sahip iki miksere verilir. Bu ikisi, iki bant geçiş filtresine bağlıdır. Bu kombinasyonlar demodülatörler olarak hareket eder ve karar devresi hangi çıktının daha olası olduğunu seçer ve onu herhangi bir dedektörden seçer. İki sinyalin minimum frekans ayrımı vardır.
Her iki demodülatör için, her birinin bant genişliği bit hızlarına bağlıdır. Bu senkronize demodülatör, asenkron tip demodülatörlerden biraz karmaşıktır.
Phase Shift Keying (PSK)belirli bir zamanda sinüs ve kosinüs girişlerini değiştirerek taşıyıcı sinyalin fazının değiştirildiği dijital modülasyon tekniğidir. PSK tekniği, kablosuz LAN'lar, biyo-metrik, temassız işlemler, RFID ve Bluetooth iletişimi ile birlikte yaygın olarak kullanılmaktadır.
PSK, sinyalin kaydırıldığı aşamalara bağlı olarak iki tiptedir. Onlar -
İkili Faz Kaydırma Anahtarlama (BPSK)
Bu aynı zamanda 2-fazlı PSK veya Phase Reversal Keying olarak da adlandırılır. Bu teknikte, sinüs dalgası taşıyıcısı, 0 ° ve 180 ° gibi iki faz tersini alır.
BPSK, mesajın dijital bilgi olması için temelde bir Çift Taraflı Bant Bastırılmış Taşıyıcı (DSBSC) modülasyon şemasıdır.
Dörtlü Faz Kaydırma Anahtarlama (QPSK)
Bu, sinüs dalgası taşıyıcısının 0 °, 90 °, 180 ° ve 270 ° gibi dört faz ters çevirme yaptığı faz kaydırmalı anahtarlama tekniğidir.
Bu tür teknikler daha da genişletilirse, PSK, ihtiyaca bağlı olarak sekiz veya on altı değerde de yapılabilir.
BPSK Modülatör
İkili Faz Kaydırma Anahtarlamasının blok diyagramı, bir giriş olarak taşıyıcı sinüs dalgasına ve diğer giriş olarak ikili diziye sahip olan denge modülatöründen oluşur. Aşağıdaki diyagramatik gösterimdir.
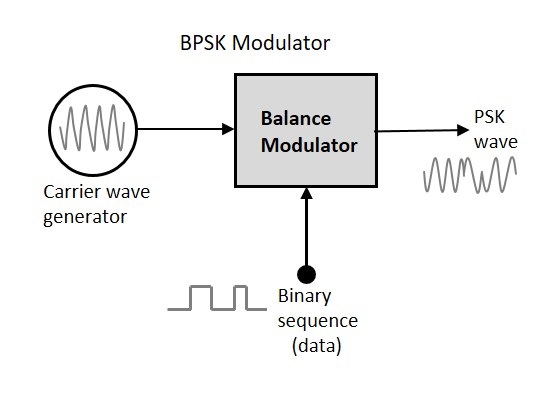
BPSK modülasyonu, girişte uygulanan iki sinyali çarpan bir denge modülatörü kullanılarak yapılır. Sıfır ikili giriş için, faz0° ve yüksek bir giriş için fazın tersine çevrilmesi 180°.
Aşağıda, BPSK Modüle edilmiş çıkış dalgasının verilen girişle birlikte şematik gösterimi bulunmaktadır.
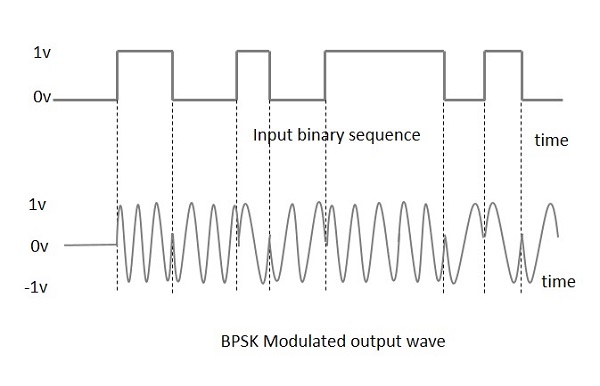
Modülatörün çıkış sinüs dalgası, doğrudan giriş taşıyıcısı veya veri sinyalinin bir fonksiyonu olan ters çevrilmiş (180 ° faz kaydırmalı) giriş taşıyıcısı olacaktır.
BPSK Demodülatör
BPSK demodülatörünün blok diyagramı, yerel osilatör devresine sahip bir karıştırıcı, bir bant geçiş filtresi, iki girişli bir dedektör devresinden oluşur. Şema aşağıdaki gibidir.
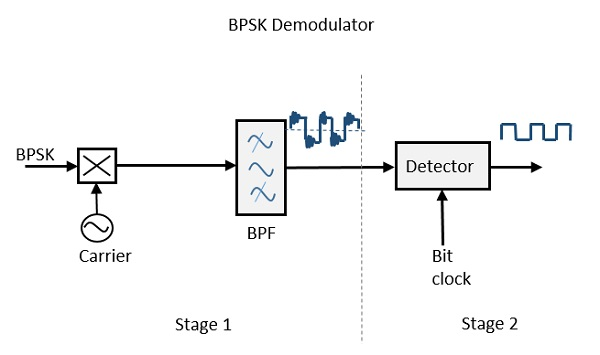
Band sınırlı mesaj sinyali, mikser devresi ve bant geçiş filtresi yardımıyla kurtarılarak, demodülasyonun ilk aşaması tamamlanır. Bant sınırlı olan baz bant sinyali elde edilir ve bu sinyal ikili mesaj bit akışını yeniden oluşturmak için kullanılır.
Demodülasyonun bir sonraki aşamasında, orijinal ikili mesaj sinyalini üretmek için detektör devresinde bit saat hızına ihtiyaç vardır. Bit hızı, taşıyıcı frekansın bir alt katı ise, bit saati yeniden oluşturulması basitleştirilir. Devreyi kolayca anlaşılır kılmak için , tespitin 2. aşamasında bir karar verme devresi de eklenebilir .
Quadrature Phase Shift Keying (QPSK) BPSK'nın bir varyasyonudur ve aynı zamanda bir seferde iki bit dijital bilgi gönderen bir Çift Taraflı Bant Bastırılmış Taşıyıcı (DSBSC) modülasyon şemasıdır. bigits.
Dijital bitleri bir dizi dijital akışa dönüştürmek yerine, bunları bit çiftlerine dönüştürür. Bu, veri bit hızını yarıya düşürerek diğer kullanıcılar için alan sağlar.
QPSK Modülatör
QPSK Modülatör, bir bit ayırıcı, yerel osilatörlü iki çarpan, 2 bitlik bir seriden paralele dönüştürücü ve bir yaz devresi kullanır. Aşağıdakiler aynı blok diyagramdır.

Modülatör girişine de, mesajı sinyalin çift bitler (örneğin, 2 nci bit 4 inci biti, 6 inci biti, vb) ve tek bitler (örneğin, 1 bit 3 rd bit, 5 inci biti, vb) ayrılır bit ayırıcı tarafından ve tek BPSK üretmek için aynı taşıyıcıyla çarpılır (PSKI) ve hatta BPSK ( PSKQ). PSKQ sinyal zaten modüle edilmeden önce faz 90 ° kaydırılır.
İki bitlik giriş için QPSK dalga biçimi aşağıdaki gibidir ve ikili girişlerin farklı örnekleri için modüle edilmiş sonucu gösterir.
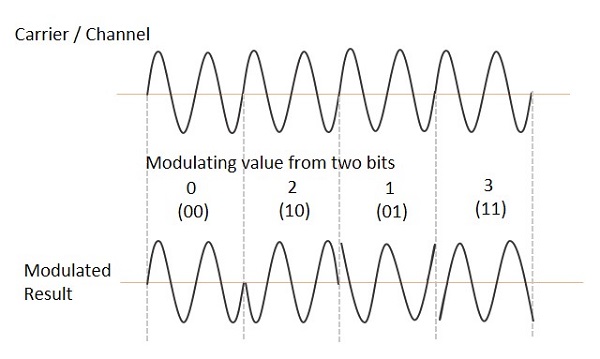
QPSK Demodülatör
QPSK Demodülatör, yerel osilatörlü iki ürün demodülatör devresi, iki bant geçiş filtresi, iki entegratör devresi ve seri dönüştürücüye paralel 2 bitlik bir dönüştürücü kullanır. Aynı şema aşağıdadır.
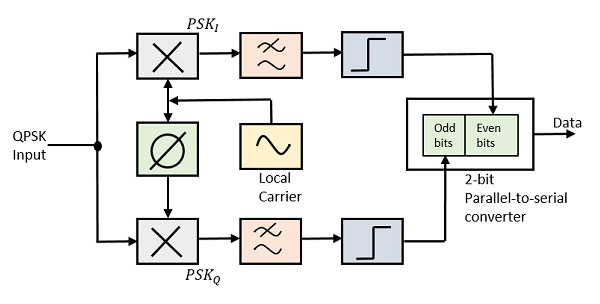
Demodülatörün girişindeki iki ürün dedektörü aynı anda iki BPSK sinyalini demodüle eder. Bit çifti burada orijinal verilerden kurtarılır. Bu sinyaller işlendikten sonra paralelden seri dönüştürücüye aktarılır.
İçinde Differential Phase Shift Keying (DPSK)modüle edilmiş sinyalin fazı, önceki sinyal elemanına göre kaydırılır. Burada hiçbir referans sinyali dikkate alınmaz. Sinyal aşaması, önceki elemanın yüksek veya düşük durumunu takip eder. Bu DPSK tekniğinin bir referans osilatöre ihtiyacı yoktur.
Aşağıdaki şekil DPSK'nın model dalga biçimini temsil etmektedir.
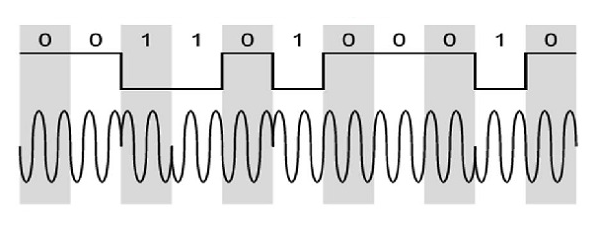
Yukarıdaki şekilden, eğer veri biti Düşük, yani 0 ise, o zaman sinyal fazının tersine çevrilmediği, olduğu gibi devam ettiği görülmektedir. Veriler Yüksek, yani 1 ise, sinyalin fazı, NRZI'de olduğu gibi tersine çevrilir, 1'de ters çevrilir (bir tür diferansiyel kodlama).
Yukarıdaki dalga biçimini gözlemlersek, Yüksek durumun bir M modüle edici sinyalde ve Düşük durum bir W modülasyon sinyalinde.
DPSK Modülatör
DPSK, referans faz sinyalinin olmadığı bir BPSK tekniğidir. Burada iletilen sinyalin kendisi bir referans sinyal olarak kullanılabilir. DPSK Modülatörünün diyagramı aşağıdadır.
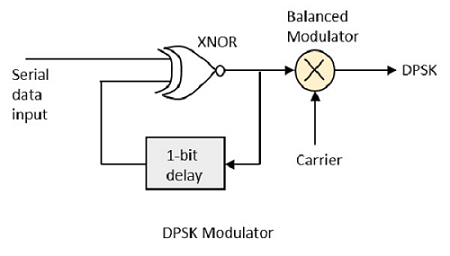
DPSK, iki farklı sinyali, yani taşıyıcı ve her biri 180 ° faz kaymalı modülasyon sinyalini kodlar. Seri veri girişi XNOR geçidine verilir ve çıkış yine 1 bitlik gecikmeyle diğer girişe geri beslenir. Taşıyıcı sinyal ile birlikte XNOR geçidinin çıkışı, DPSK modüle edilmiş sinyali üretmek için denge modülatörüne verilir.
DPSK Demodülatör
DPSK demodülatöründe, tersine çevrilmiş bitin fazı, önceki bitin fazı ile karşılaştırılır. DPSK demodülatörünün blok diyagramı aşağıdadır.

Yukarıdaki şekilden, denge modülatörüne 1 bit gecikme girişi ile birlikte DPSK sinyali verildiği açıktır. Bu sinyal, LPF yardımı ile daha düşük frekanslarla sınırlandırılmak üzere yapılmıştır. Daha sonra, orijinal ikili verileri çıktı olarak kurtarmak için bir karşılaştırıcı veya bir Schmitt tetikleme devresi olan bir şekillendirici devresine geçirilir.
İkili kelime iki biti temsil eder. M belirli sayıda ikili değişken için olası koşulların, düzeylerin veya kombinasyonların sayısına karşılık gelen bir rakamı temsil eder.
Bu, veri iletimi için kullanılan ve bir seferde bir bit yerine iki veya daha fazla bitin iletildiği dijital modülasyon tekniğidir. Çoklu bit aktarımı için tek bir sinyal kullanıldığından, kanal bant genişliği azaltılır.
M-ary Denklemi
Gerilim seviyeleri, frekanslar, fazlar ve genlik gibi dört koşul altında bir dijital sinyal verilirse, o zaman M = 4.
Belirli sayıda koşulu üretmek için gerekli bit sayısı matematiksel olarak şu şekilde ifade edilir:
$$ N = \ log_ {2} {M} $$
Nerede
N gerekli bit sayısı
M olası koşulların, düzeylerin veya kombinasyonların sayısıdır N bitler.
Yukarıdaki denklem şu şekilde yeniden düzenlenebilir:
$$ 2 ^ N = M $$
Örneğin, iki bit ile, 22 = 4 koşullar mümkündür.
M-ary Teknik Türleri
Genel olarak, vericinin girişinde ikiden fazla modülasyon seviyesine sahip dijital girişlere izin verildiğinden, çok seviyeli (M-ary) modülasyon teknikleri dijital iletişimde kullanılır. Bu nedenle, bu teknikler bant genişliği açısından verimlidir.
Birçok M-ary modülasyon tekniği vardır. Bu tekniklerden bazıları, genlik, faz ve frekans gibi taşıyıcı sinyalin bir parametresini modüle eder.
M-ary SOR
Buna M-ary Genlik Kaydırma Anahtarlaması (M-ASK) veya M-ary Darbe Genlik Modülasyonu (PAM) denir.
amplitude taşıyıcı sinyalin M farklı seviyeler.
M-ary ASK'nın Temsili
$ S_m (t) = A_mcos (2 \ pi f_ct) \ quad A_m \ epsilon {(2m - 1 - M) \ Delta, m = 1,2 ... \: .M} \ quad ve \ quad 0 \ leq t \ leq T_s $
M-ary ASK'nın öne çıkan bazı özellikleri şunlardır:
- Bu yöntem aynı zamanda PAM'da da kullanılmaktadır.
- Uygulaması basittir.
- M-ary ASK gürültüye ve bozulmaya karşı hassastır.
M-ary FSK
Bu, Çoklu Frekans Kaydırma Anahtarlaması (M-ary FSK) olarak adlandırılır.
frequency taşıyıcı sinyalin M farklı seviyeler.
M-ary FSK'nın temsili
$ S_i (t) = \ sqrt {\ frac {2E_s} {T_s}} \ cos \ left (\ frac {\ pi} {T_s} \ left (n_c + i \ right) t \ right) $ $ 0 \ leq t \ leq T_s \ quad ve \ quad i = 1,2,3 ... \: ..M $
$ F_c = \ frac {n_c} {2T_s} $ bazı sabit tamsayı için n.
M-ary FSK'nın öne çıkan bazı özellikleri şunlardır:
ASK kadar gürültüye duyarlı değildir.
İletilen M sinyal sayısı enerji ve süre bakımından eşittir.
Sinyaller $ \ frac {1} {2T_s} $ Hz ile ayrılır ve sinyalleri birbirine ortogonal hale getirir.
Dan beri M sinyaller ortogonaldir, sinyal alanında kalabalıklaşma yoktur.
M-ary FSK'nın bant genişliği verimliliği, artışla birlikte azalır ve güç verimliliği artar. M.
M-ary PSK
Bu, Çoklu Faz Kaymalı Anahtarlama (M-ary PSK) olarak adlandırılır.
phase taşıyıcı sinyalin M farklı seviyeler.
M-ary PSK'nın temsili
$ S_i (t) = \ sqrt {\ frac {2E} {T}} \ cos \ left (w_o t + \ phi _it \ right) $ $ 0 \ leq t \ leq T \ quad ve \ quad i = 1,2 ... M $
$$ \ phi _i \ left (t \ right) = \ frac {2 \ pi i} {M} \ quad burada \ quad i = 1,2,3 ... \: ... M $$
M-ary PSK'nın öne çıkan bazı özellikleri şunlardır:
Zarf, daha fazla faz olasılığı ile sabittir.
Bu yöntem, uzay iletişiminin ilk günlerinde kullanıldı.
ASK ve FSK'dan daha iyi performans.
Alıcıda minimum faz tahmin hatası.
M-ary PSK'nın bant genişliği verimliliği artar ve güç verimliliği artar. M.
Şimdiye kadar farklı modülasyon tekniklerini tartıştık. Tüm bu tekniklerin çıktısı, şu şekilde temsil edilen ikili bir dizidir:1s ve 0s. Bu ikili veya dijital bilginin, daha fazla tartışılacak birçok türü ve formu vardır.
Bilgi, ister analog ister dijital olsun, bir iletişim sisteminin kaynağıdır. Information theory bilginin nicelendirilmesi, depolanması ve iletişimi ile birlikte bilginin kodlanması çalışmasına matematiksel bir yaklaşımdır.
Olayların Oluşma Koşulları
Bir olayı ele alırsak, üç gerçekleşme koşulu vardır.
Olay gerçekleşmediyse, bir durum vardır uncertainty.
Olay yeni meydana gelmişse, şu koşul vardır: surprise.
Olay meydana geldiyse, bir zaman geriye, bazılarına sahip olma koşulu vardır. information.
Bu üç olay farklı zamanlarda gerçekleşir. Bu koşullardaki fark, olayların gerçekleşme olasılıkları hakkında bilgi edinmemize yardımcı olur.
Entropi
Bir olayın meydana gelme olasılıklarını, ne kadar şaşırtıcı veya belirsiz olacağını gözlemlediğimizde, bu, olayın kaynağından gelen bilginin ortalama içeriği hakkında bir fikir edinmeye çalıştığımız anlamına gelir.
Entropy kaynak sembolü başına ortalama bilgi içeriğinin bir ölçüsü olarak tanımlanabilir. Claude Shannon, "Bilgi Teorisinin babası" bunun için bir formül sağladı:
$$ H = - \ sum_ {i} p_i \ log_ {b} p_i $$
Nerede pi karakter numarasının oluşma olasılığı i belirli bir karakter akışından ve bkullanılan algoritmanın temelidir. Bu nedenle, bu aynı zamandaShannon’s Entropy.
Kanal çıkışını gözlemledikten sonra kanal girişi hakkında kalan belirsizlik miktarı, Conditional Entropy. $ H (x \ mid y) $ ile gösterilir
Karşılıklı bilgi
Çıktısı şu olan bir kanalı düşünelim: Y ve girdi X
Önceki belirsizlik için entropi olsun X = H(x)
(Bu, girdi uygulanmadan önce varsayılır)
Çıktının belirsizliğini bilmek için, girdi uygulandıktan sonra, Koşullu Entropiyi düşünelim. Y = yk
$$ H \ left (x \ mid y_k \ sağ) = \ sum_ {j = 0} ^ {j - 1} p \ left (x_j \ mid y_k \ sağ) \ log_ {2} \ left [\ frac {1 } {p (x_j \ mid y_k)} \ sağ] $$
Bu, $ H (X \ mid y = y_0) \: ... \: ... \: ... \: ... \: ... \: H (X \ mid y = y_k) $ sırasıyla $ p (y_0) \: ... \: ... \: ... \: ... \: p (y_ {k-1)} $ olasılıkları ile.
Çıktı alfabesi için $ H (X \ mid y = y_k) $ ortalama değeri y -
$ H \ sol (X \ orta Y \ sağ) = \ displaystyle \ toplam \ limits_ {k = 0} ^ {k - 1} H \ sol (X \ orta y = y_k \ sağ) p \ sol (y_k \ sağ ) $
$ = \ displaystyle \ sum \ limits_ {k = 0} ^ {k - 1} \ displaystyle \ sum \ limits_ {j = 0} ^ {j - 1} p \ sol (x_j \ orta y_k \ sağ) p \ sol (y_k \ sağ) \ log_ {2} \ sol [\ frac {1} {p \ left (x_j \ mid y_k \ sağ)} \ sağ] $
$ = \ displaystyle \ sum \ limits_ {k = 0} ^ {k - 1} \ displaystyle \ sum \ limits_ {j = 0} ^ {j - 1} p \ sol (x_j, y_k \ sağ) \ log_ {2 } \ sol [\ frac {1} {p \ left (x_j \ mid y_k \ sağ)} \ sağ] $
Şimdi, her iki belirsizlik koşulunu da göz önünde bulundurarak (girdileri uygulamadan önce ve sonra), farkın, yani $ H (x) - H (x \ mid y) $ 'ın, çözülen kanal girdisi hakkındaki belirsizliği temsil etmesi gerektiğini biliyoruz. kanal çıkışını gözlemleyerek.
Bu, Mutual Information kanalın.
Karşılıklı Bilgiyi $ I (x; y) $ olarak ifade ederek, her şeyi aşağıdaki gibi bir denklemde yazabiliriz
$$ I (x; y) = H (x) - H (x \ mid y) $$
Dolayısıyla, bu Karşılıklı Bilginin eşitlikçi temsilidir.
Karşılıklı bilginin özellikleri
Bunlar Karşılıklı bilginin özellikleridir.
Bir kanalın karşılıklı bilgisi simetriktir.
$$ I (x; y) = I (y; x) $$
Karşılıklı bilgi olumsuz değildir.
$$ I (x; y) \ geq 0 $$
Karşılıklı bilgi, kanal çıktısının entropisi cinsinden ifade edilebilir.
$$ I (x; y) = H (y) - H (y \ mid x) $$
$ H (y \ mid x) $ koşullu bir entropidir
Bir kanalın karşılıklı bilgisi, kanal girişi ve kanal çıktısının ortak entropisiyle ilgilidir.
$$ I (x; y) = H (x) + H (y) - H (x, y) $$
$ H (x, y) $ ortak entropisi şu şekilde tanımlanır:
$$ H (x, y) = \ displaystyle \ sum \ limits_ {j = 0} ^ {j-1} \ displaystyle \ sum \ limits_ {k = 0} ^ {k-1} p (x_j, y_k) \ log_ {2} \ left (\ frac {1} {p \ left (x_i, y_k \ sağ)} \ sağ) $$
Kanal Kapasitesi
Şimdiye kadar karşılıklı bilgileri tartıştık. Bir sinyalleme aralığı anında maksimum ortalama karşılıklı bilgi, ayrık bir hafızasız kanal tarafından iletildiğinde, maksimum güvenilir veri aktarım hızının olasılıkları şu şekilde anlaşılabilir:channel capacity.
İle gösterilir C ve ölçülür bits per channel kullanın.
Ayrık Belleksiz Kaynak
Verilerin birbirini takip eden aralıklarla gönderildiği ve önceki değerlerden bağımsız olan bir kaynak şu şekilde adlandırılabilir: discrete memoryless source.
Bu kaynak, sürekli bir zaman aralığı için değil, farklı zaman aralıkları için dikkate alındığı için ayrıktır. Bu kaynak, önceki değerler dikkate alınmaksızın her an taze olduğu için hafızasızdır.
Ayrık bir belleksiz kaynak tarafından üretilen Kod, verimli bir şekilde temsil edilmelidir ki bu, iletişimde önemli bir sorundur. Bunun gerçekleşmesi için, bu kaynak kodları temsil eden kod sözcükleri vardır.
Örneğin, telgrafta, alfabelerin şu şekilde ifade edildiği Mors kodunu kullanıyoruz Marks ve Spaces. Eğer mektupE Çoğunlukla kullanılan kabul edilir, ile gösterilir “.” Oysa mektup Q nadiren kullanılan, ile gösterilir “--.-”
Blok diyagrama bir göz atalım.
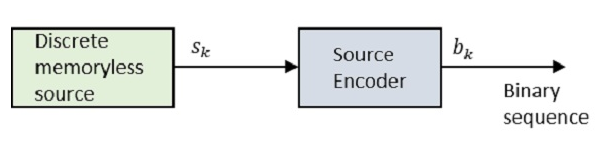
Nerede Sk ayrık belleksiz kaynağın çıkışıdır ve bk ile temsil edilen kaynak kodlayıcının çıktısıdır 0s ve 1s.
Kodlanmış dizi, alıcıda uygun şekilde kodu çözülecek şekildedir.
Kaynağın bir alfabesi olduğunu varsayalım. k farklı semboller ve kth sembol Sk olasılıkla oluşur Pk, nerede k = 0, 1…k-1.
İkili kod kelimesi sembole atansın Skuzunluğu olan kodlayıcı tarafından lk, bit cinsinden ölçülür.
Bu nedenle, kaynak kodlayıcının ortalama kod kelimesi uzunluğunu L olarak tanımlarız.
$$ \ overline {L} = \ displaystyle \ sum \ limits_ {k = 0} ^ {k-1} p_kl_k $$
L kaynak sembolü başına ortalama bit sayısını temsil eder
$ L_ {min} = \: minimum \: olası \: değer \: / \: \ overline {L} $
Sonra coding efficiency olarak tanımlanabilir
$$ \ eta = \ frac {L {min}} {\ overline {L}} $$
$ \ Overline {L} \ geq L_ {min} $ ile $ \ eta \ leq 1 $ elde edeceğiz
Bununla birlikte, kaynak kodlayıcı $ \ eta = 1 $ olduğunda verimli kabul edilir
Bunun için $ L_ {min} $ değeri belirlenmelidir.
Şu tanıma bakalım: "Ayrık bir belleksiz $ H (\ delta) $ entropi kaynağı verildiğinde, ortalama kod-kelime uzunluğuL herhangi bir kaynak kodlaması için $ \ overline {L} \ geq H (\ delta) $ olarak sınırlandırılmıştır. "
Daha basit kelimelerde, kod kelimesi (örnek: KUYRUK kelimesi için mors kodu -.- ..-. ..-.) Her zaman kaynak koddan büyük veya ona eşittir (örnekte KUYRU). Bu, kod kelimesindeki sembollerin kaynak koddaki alfabelerden büyük veya bunlara eşit olduğu anlamına gelir.
Dolayısıyla, $ L_ {min} = H (\ delta) $ ile, Entropy $ H (\ delta) $ açısından kaynak kodlayıcının verimliliği şu şekilde yazılabilir:
$$ \ eta = \ frac {H (\ delta)} {\ overline {L}} $$
Bu kaynak kodlama teoremi olarak adlandırılır noiseless coding theoremhatasız bir kodlama oluşturduğu için. Olarak da adlandırılırShannon’s first theorem.
Bir kanalda bulunan gürültü, bir dijital iletişim sisteminin giriş ve çıkış dizileri arasında istenmeyen hatalar yaratır. Hata olasılığı çok düşük olmalı,nearly ≤ 10-6 güvenilir bir iletişim için.
Bir iletişim sistemindeki kanal kodlaması, sistemin güvenilirliğini artırmak için bir kontrol ile artıklık getirir. Kaynak kodlaması, sistemin verimliliğini artırmak için fazlalığı azaltır.
Kanal kodlaması iki bölümden oluşur.
Mapping bir kanal giriş sırasına gelen veri dizisi.
Inverse Mapping kanal çıktı dizisini bir çıktı veri dizisine dönüştürür.
Nihai hedef, genel etkisinin channel noise minimize edilmelidir.
Haritalama, bir kodlayıcı yardımıyla verici tarafından yapılırken, ters eşleme alıcıdaki kod çözücü tarafından yapılır.
Kanal Kodlaması
Ayrık belleksiz bir kanalı düşünelim (δ) Entropi ile H (δ)
Ts saniyede δ'nin verdiği sembolleri gösterir
Kanal kapasitesi ile gösterilir C
Kanal her biri için kullanılabilir Tc saniye
Bu nedenle, kanalın maksimum kapasitesi C/Tc
Gönderilen veri = $ \ frac {H (\ delta)} {T_s} $
$ \ Frac {H (\ delta)} {T_s} \ leq \ frac {C} {T_c} $ ise bu, iletimin iyi olduğu ve küçük bir hata olasılığı ile yeniden üretilebileceği anlamına gelir.
Bunda $ \ frac {C} {T_c} $, kanal kapasitesinin kritik oranıdır.
$ \ Frac {H (\ delta)} {T_s} = \ frac {C} {T_c} $ ise, sistemin kritik bir oranda sinyal verdiği söylenir.
Tersine, eğer $ \ frac {H (\ delta)} {T_s}> \ frac {C} {T_c} $ ise, iletim mümkün değildir.
Bu nedenle, maksimum iletim hızı, ayrık bir hafızasız kanal üzerinden gerçekleşebilen güvenilir hatasız mesajlar için kanal kapasitesinin kritik hızına eşittir. Bu denirChannel coding theorem.
Gürültü veya Hata, iletişim sisteminin güvenilirliğini bozan sinyaldeki ana sorundur. Error control codinghataların oluşumunu kontrol etmek için yapılan kodlama prosedürüdür. Bu teknikler Hata Algılama ve Hata Düzeltmede yardımcı olur.
Kendilerine uygulanan matematiksel ilkelere bağlı olarak birçok farklı hata düzeltme kodu vardır. Ancak tarihsel olarak bu kodlar,Linear block codes ve Convolution codes.
Doğrusal Blok Kodları
Doğrusal blok kodlarında, eşlik bitleri ve mesaj bitlerinin doğrusal bir kombinasyonu vardır, bu, sonuçtaki kod sözcüğünün herhangi iki kod sözcüğünün doğrusal birleşimi olduğu anlamına gelir.
Aşağıdakileri içeren bazı veri bloklarını ele alalım: kher bloktaki bitler. Bu bitler, sahip olan bloklarla eşleştirilir.nher bloktaki bitler. Burayan daha büyüktür k. Verici, gereksiz bitler ekler.(n-k)bitler. Orank/n ... code rate. İle gösterilirr ve değeri r dır-dir r < 1.
(n-k) buraya eklenen bitler parity bits. Eşlik bitleri, hata tespiti ve hata düzeltmede ve ayrıca verilerin bulunmasında yardımcı olur. İletilen verilerde, kod sözcüğünün en soldaki biti mesaj bitlerine karşılık gelir ve kod sözcüğünün en sağdaki biti, eşlik bitlerine karşılık gelir.
Sistematik Kod
Herhangi bir doğrusal blok kodu, değiştirilene kadar sistematik bir kod olabilir. Bu nedenle, değiştirilmemiş bir blok kodu,systematic code.
Aşağıdaki temsilidir structure of code word, tahsislerine göre.

Mesaj değiştirilmezse sistematik kod olarak adlandırılır. Bu, verilerin şifrelenmesinin verileri değiştirmemesi gerektiği anlamına gelir.
Evrişim Kodları
Şimdiye kadar doğrusal kodlarda, sistematik değiştirilmemiş kodun tercih edildiğini tartıştık. İşte toplamın verilerin aktarılırsa bitler, k bitler mesaj bitleridir ve (n-k) bitler eşlik bitleridir.
Kodlama sürecinde, eşlik bitleri tüm verilerden çıkarılır ve mesaj bitleri kodlanır. Şimdi, eşlik bitleri tekrar eklenir ve tüm veriler yeniden kodlanır.
Aşağıdaki şekil, bilgi aktarımı için kullanılan veri blokları ve veri akışı için bir örnek vermektedir.

Yukarıda belirtilen tüm süreç sıkıcıdır ve sakıncaları vardır. Tamponun tahsisi, sistem meşgul olduğunda burada ana problemdir.
Bu dezavantaj, evrişim kodlarında açıklanmıştır. Tüm veri akışına sembollerin atandığı ve daha sonra iletildiği yer. Veriler bir bit akışı olduğundan, depolama için ara belleğe gerek yoktur.
Hamming Kodları
Kod kelimesinin doğrusallık özelliği, iki kod kelimesinin toplamının aynı zamanda bir kod kelimesi olmasıdır. Hamming kodları,linear error correcting iki bite kadar hatayı algılayabilen veya düzeltilmemiş hatalar tespit edilmeden bir bitlik hataları düzeltebilen kodlar.
Hamming kodlarını kullanırken, ekstra eşlik bitleri, tek bitlik bir hatayı tanımlamak için kullanılır. Bir bitlik modelden diğerine geçmek için, verilerde birkaç bit değiştirilmelidir. Bu kadar bit sayısı şu şekilde adlandırılabilir:Hamming distance. Eşliğin uzaklığı 2 ise, tek bitlik çevirme algılanabilir. Ancak bu düzeltilemez. Ayrıca, herhangi iki bitlik dönüşler algılanamaz.
Bununla birlikte, Hamming kodu, hata tespiti ve düzeltmesinde daha önce tartışılanlardan daha iyi bir prosedürdür.
BCH Kodları
BCH kodları, mucitlerin adını taşır Bose, Chaudari ve Hocquenghem. BCH kod tasarımı sırasında, düzeltilecek sembollerin sayısı üzerinde kontrol vardır ve bu nedenle çoklu bit düzeltmesi mümkündür. BCH kodları, hata düzeltme kodlarında güçlü bir tekniktir.
Herhangi bir pozitif tam sayı için m ≥ 3 ve t < 2m-1bir BCH ikili kodu var. Bu tür kodun parametreleri aşağıdadır.
Blok uzunluğu n = 2m-1
Eşlik denetimi basamaklarının sayısı n - k ≤ mt
Minimum mesafe dmin ≥ 2t + 1
Bu kod şu şekilde çağrılabilir: t-error-correcting BCH code.
Döngüsel Kodlar
Kod sözcüklerinin döngüsel özelliği, bir kod sözcüğünün herhangi bir döngüsel kaydırmasının aynı zamanda bir kod sözcüğü olmasıdır. Döngüsel kodlar bu döngüsel özelliği izler.
Doğrusal bir kod için Cher kod sözcüğü ie ise, C = (C1, C2, ...... Cn)C'den bileşenlerin döngüsel sağa kayması vardır, bu bir kod sözcüğü haline gelir. Bu sağa kayma eşittirn-1döngüsel sola kaymalar. Bu nedenle, herhangi bir vardiya altında değişmezdir. Doğrusal kodC, herhangi bir vardiyada değişmez olduğu için, bir Cyclic code.
Döngüsel kodlar, hata düzeltme için kullanılır. Çoğunlukla çift hataları ve seri hataları düzeltmek için kullanılırlar.
Bu nedenle, bunlar alıcıda tespit edilmesi gereken birkaç hata düzeltme kodlarıdır. Bu kodlar hataların ortaya çıkmasını engeller ve iletişimi bozar. Ayrıca, sinyalin istenmeyen alıcılar tarafından dinlenmesini de engeller. Bunu başarmak için bir sonraki bölümde tartışılan bir sinyalleme tekniği sınıfı vardır.
Güvenli bir iletişim sağlamak için bir sinyal iletmeden önce toplu bir sinyalizasyon teknikleri sınıfı kullanılır. Spread Spectrum Modulation. Yaygın spektrum iletişim tekniğinin temel avantajı, ister kasıtlı ister kasıtsız olsun, “girişimi” önlemektir.
Bu tekniklerle modüle edilen sinyallerin karışması zordur ve karıştırılamaz. Resmi erişimi olmayan bir saldırganın onları kırmasına asla izin verilmez. Dolayısıyla bu teknikler askeri amaçlarla kullanılmaktadır. Bu yayılmış spektrum sinyalleri, düşük güç yoğunluğunda iletilir ve geniş bir sinyal yayılımına sahiptir.
Sözde Gürültü Dizisi
Kodlanmış bir dizi 1s ve 0s belirli oto-korelasyon özellikleriyle Pseudo-Noise coding sequenceyaygın spektrum tekniklerinde kullanılır. Bir döngüsel kod türü olan maksimum uzunlukta bir dizidir.
Dar bant ve Yayılı spektrum Sinyaller
Hem Dar bant hem de Yayılı spektrum sinyalleri, aşağıdaki şekillerde gösterildiği gibi frekans spektrumları gözlemlenerek kolayca anlaşılabilir.
Dar bant Sinyaller
Dar bantlı sinyaller, aşağıdaki frekans spektrumu şeklinde gösterildiği gibi yoğunlaştırılmış sinyal gücüne sahiptir.
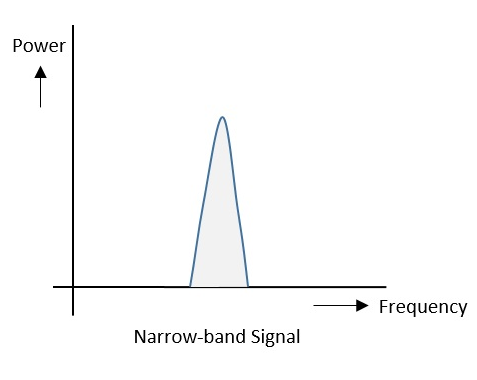
Aşağıda özelliklerinden bazıları verilmiştir -
- Sinyal bandı dar bir frekans aralığını işgal eder.
- Güç yoğunluğu yüksektir.
- Enerji yayılımı düşük ve konsantredir.
Özellikler iyi olsa da, bu sinyaller parazite eğilimlidir.
Spread Spectrum Signals
Yaygın spektrum sinyalleri, aşağıdaki frekans spektrumu şeklinde gösterildiği gibi dağıtılmış sinyal gücüne sahiptir.
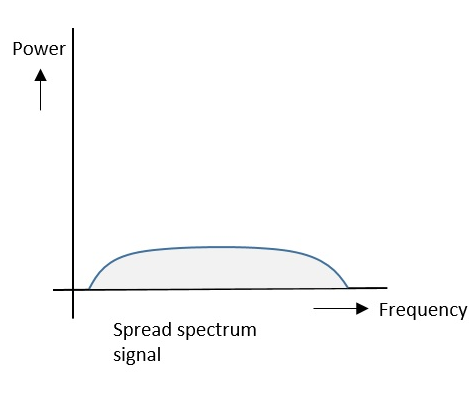
Aşağıda özelliklerinden bazıları verilmiştir -
- Sinyal bandı geniş bir frekans aralığını işgal eder.
- Güç yoğunluğu çok düşük.
- Enerji çok yaygındır.
Bu özelliklerle, yayılmış spektrum sinyalleri girişime veya sıkışmaya karşı oldukça dirençlidir. Birden çok kullanıcı, birbirine müdahale etmeden aynı yayılı spektrum bant genişliğini paylaşabildiğinden, bunlar şöyle adlandırılabilir:multiple access techniques.
FHSS ve DSSS / CDMA
Yayılı spektrum çoklu erişim teknikleri, minimum gerekli RF bant genişliğinden daha büyük bir iletim bant genişliğine sahip sinyalleri kullanır.
Bunlar iki türdendir.
- Frekans Atlamalı Yayılı Spektrum (FHSS)
- Doğrudan Sıralı Yayılı Spektrum (DSSS)
Frekans Atlamalı Yayılı Spektrum (FHSS)
Bu, kullanıcıların belirli bir zaman aralığında kullanım frekanslarını birinden diğerine değiştirmeleri için yapılan frekans atlamalı tekniktir, dolayısıyla frequency hopping. Örneğin, belirli bir süre için gönderen 1'e bir frekans tahsis edildi. Şimdi, bir süre sonra, gönderen 1 diğer frekansa atlar ve gönderen 2, daha önce gönderen 1 tarafından kullanılan ilk frekansı kullanır. Buna,frequency reuse.
Verilerin frekansları, güvenli bir iletim sağlamak için birinden diğerine atlanır. Her frekans sıçraması için harcanan zaman miktarı şu şekilde adlandırılır:Dwell time.
Doğrudan Sıralı Yayılı Spektrum (DSSS)
Bir kullanıcı bu DSSS tekniğini kullanarak veri göndermek istediğinde, kullanıcı verilerinin her bir biti olarak adlandırılan gizli bir kodla çarpılır. chipping code. Bu yonga kodu, orijinal mesajla çarpılan ve iletilen yayılma kodundan başka bir şey değildir. Alıcı, orijinal mesajı almak için aynı kodu kullanır.
FHSS ve DSSS / CDMA arasında karşılaştırma
Her iki yayılı spektrum tekniği de özellikleri açısından popülerdir. Net bir anlayışa sahip olmak için, karşılaştırmalarına bir göz atalım.
| FHSS | DSSS / CDMA |
|---|---|
| Birden çok frekans kullanılır | Tek frekans kullanılır |
| Herhangi bir anda kullanıcının frekansını bulmak zor | Kullanıcı frekansı, bir kez tahsis edildiğinde her zaman aynıdır |
| Frekansın yeniden kullanımına izin verilir | Frekansın yeniden kullanımına izin verilmiyor |
| Gönderenin beklemesine gerek yok | Spektrum meşgulse göndericinin beklemesi gerekir |
| Sinyalin güç gücü yüksek | Sinyalin güç gücü düşük |
| Daha güçlüdür ve engelleri aşar | FHSS'ye göre daha zayıf |
| Parazitten asla etkilenmez | Girişimden etkilenebilir |
| O daha ucuz | Bu pahalı |
| Bu yaygın olarak kullanılan tekniktir | Bu teknik sık kullanılmamaktadır |
Yayılmış Spektrumun Avantajları
Yayılma spektrumunun avantajları aşağıdadır -
- Çapraz konuşmanın ortadan kaldırılması
- Veri bütünlüğü ile daha iyi çıktı
- Çok yollu solmanın azaltılmış etkisi
- Daha iyi güvenlik
- Gürültüde azalma
- Diğer sistemlerle birlikte yaşama
- Daha uzun operasyon mesafeleri
- Tespit etmesi zor
- Demodüle etmek / kodunu çözmek kolay değil
- Sinyalleri karıştırmak zor
Yaygın spektrum teknikleri başlangıçta askeri kullanım için tasarlanmış olsa da, artık ticari amaçlarla yaygın olarak kullanılmaktadır.