Kaynak Kodlama Teoremi
Ayrık bir belleksiz kaynak tarafından üretilen Kod, verimli bir şekilde temsil edilmelidir ki bu, iletişimde önemli bir sorundur. Bunun gerçekleşmesi için, bu kaynak kodları temsil eden kod sözcükleri vardır.
Örneğin, telgrafta, alfabelerin şu şekilde ifade edildiği Mors kodunu kullanıyoruz Marks ve Spaces. Eğer mektupE Çoğunlukla kullanılan kabul edilir, ile gösterilir “.” Oysa mektup Q nadiren kullanılan, ile gösterilir “--.-”
Blok diyagrama bir göz atalım.
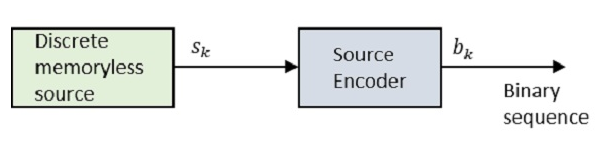
Nerede Sk ayrık belleksiz kaynağın çıkışıdır ve bk ile temsil edilen kaynak kodlayıcının çıktısıdır 0s ve 1s.
Kodlanmış dizi, alıcıda uygun şekilde kodu çözülecek şekildedir.
Kaynağın bir alfabesi olduğunu varsayalım. k farklı semboller ve kth sembol Sk olasılıkla oluşur Pk, nerede k = 0, 1…k-1.
İkili kod kelimesi sembole atansın Skuzunluğu olan kodlayıcı tarafından lk, bit cinsinden ölçülür.
Bu nedenle, kaynak kodlayıcının ortalama kod kelimesi uzunluğunu L olarak tanımlarız.
$$ \ overline {L} = \ displaystyle \ sum \ limits_ {k = 0} ^ {k-1} p_kl_k $$
L kaynak sembolü başına ortalama bit sayısını temsil eder
$ L_ {min} = \: minimum \: olası \: değer \: / \: \ overline {L} $
Sonra coding efficiency olarak tanımlanabilir
$$ \ eta = \ frac {L {min}} {\ overline {L}} $$
$ \ Overline {L} \ geq L_ {min} $ ile $ \ eta \ leq 1 $ elde edeceğiz
Bununla birlikte, kaynak kodlayıcı $ \ eta = 1 $ olduğunda verimli kabul edilir
Bunun için $ L_ {min} $ değeri belirlenmelidir.
Şu tanıma bakalım: "Ayrık bir belleksiz $ H (\ delta) $ entropi kaynağı verildiğinde, ortalama kod-kelime uzunluğuL herhangi bir kaynak kodlaması için $ \ overline {L} \ geq H (\ delta) $ olarak sınırlandırılmıştır. "
Daha basit kelimelerde, kod kelimesi (örnek: KUYRUK kelimesi için mors kodu -.- ..-. ..-.) Her zaman kaynak koddan büyük veya ona eşittir (örnekte KUYRU). Bu, kod kelimesindeki sembollerin kaynak koddaki alfabelerden büyük veya bunlara eşit olduğu anlamına gelir.
Dolayısıyla, $ L_ {min} = H (\ delta) $ ile, Entropy $ H (\ delta) $ açısından kaynak kodlayıcının verimliliği şu şekilde yazılabilir:
$$ \ eta = \ frac {H (\ delta)} {\ overline {L}} $$
Bu kaynak kodlama teoremi olarak adlandırılır noiseless coding theoremhatasız bir kodlama oluşturduğu için. Olarak da adlandırılırShannon’s first theorem.