Dijital İletişim - Örnekleme
Sampling "Sürekli zaman sinyalinin anlık değerlerini ayrı bir biçimde ölçme işlemi" olarak tanımlanır.
Sample tüm verilerden alınan ve zaman alanında sürekli olan bir veri parçasıdır.
Bir kaynak bir analog sinyal oluşturduğunda ve bunun sayısallaştırılması gerekiyorsa, 1s ve 0syani, Yüksek veya Düşük, sinyalin zaman içinde ayrıştırılması gerekir. Analog sinyalin bu ayrıklaştırılmasına Örnekleme denir.
Aşağıdaki şekil sürekli zaman sinyalini gösterir x (t) ve örneklenmiş bir sinyal xs (t). Ne zamanx (t) periyodik bir dürtü katarı ile çarpılır, örneklenmiş sinyal xs (t) elde edildi.
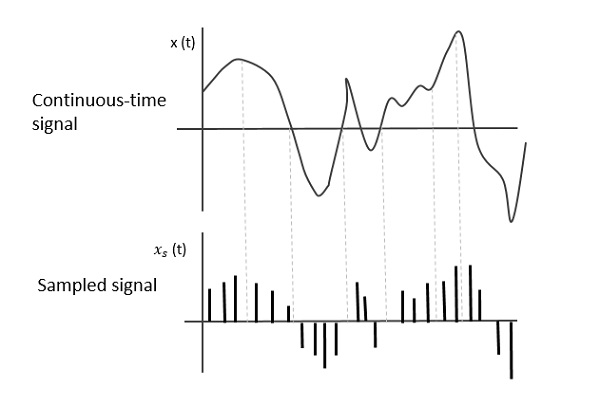
Örnekleme oranı
Sinyalleri ayırmak için örnekler arasındaki boşluk sabitlenmelidir. Bu boşluk şöyle adlandırılabilir:sampling period Ts.
$$ Örnekleme \: Sıklık = \ frac {1} {T_ {s}} = f_s $$Nerede,
$ T_ {s} $, örnekleme zamanıdır
$ f_ {s} $ örnekleme sıklığı veya örnekleme oranıdır
Sampling frequencyörnekleme süresinin tersidir. Bu örnekleme frekansı, basitçe şöyle adlandırılabilir:Sampling rate. Örnekleme hızı, saniyede veya sınırlı bir değerler kümesi için alınan örneklerin sayısını belirtir.
Bir analog sinyalin sayısallaştırılmış sinyalden yeniden oluşturulabilmesi için, örnekleme oranının yüksek oranda dikkate alınması gerekir. Örnekleme oranı, mesaj sinyalindeki verilerin kaybolmaması veya üst üste binmemesi için olmalıdır. Bunun için Nyquist oranı olarak adlandırılan bir oran sabitlendi.
Nyquist Oranı
Bir sinyalin bantla sınırlı olduğunu ve daha yüksek frekans bileşenlerinin olmadığını varsayalım WHertz. Bunun anlamı,Wen yüksek frekanstır. Böyle bir sinyal için, orijinal sinyalin etkili bir şekilde yeniden üretilmesi için, örnekleme hızı en yüksek frekansın iki katı olmalıdır.
Bunun anlamı,
$$ f_ {S} = 2W $$Nerede,
$ f_ {S} $ örnekleme oranıdır
W en yüksek frekans
Bu örnekleme oranına Nyquist rate.
Bu Nyquist oranının teorisinde Örnekleme Teoremi adlı bir teorem belirtildi.
Örnekleme Teoremi
Örnekleme teoremi olarak da adlandırılır Nyquist theorem, bantlı işlevler sınıfı için bant genişliği açısından yeterli örnekleme oranı teorisini sunar.
Örnekleme teoremi, "bir sinyal, hızda örneklenirse tam olarak yeniden üretilebilir. fs maksimum frekansın iki katından daha büyük olan W. "
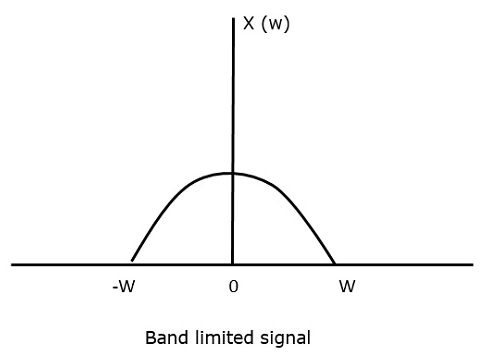
Bu örnekleme teoremini anlamak için, bant sınırlı bir sinyali, yani değeri şu olan bir sinyali düşünelim: non-zero bazıları arasında –W ve W Hertz.
Böyle bir sinyal şu şekilde temsil edilir $x(f) = 0 for |f\lvert > W$
Sürekli zaman sinyali için x (t)frekans alanındaki bant sınırlı sinyal, aşağıdaki şekilde gösterildiği gibi temsil edilebilir.
Örneklemeden sonra bile bilgi kaybının olmaması gereken bir örnekleme sıklığına ihtiyacımız var. Bunun için, örnekleme frekansının maksimum frekansın iki katı olması gereken Nyquist oranına sahibiz. Kritik örnekleme oranıdır.
Eğer sinyal x(t) Nyquist hızının üzerinde örneklendiğinde, orijinal sinyal geri kazanılabilir ve Nyquist hızının altında örneklenirse sinyal geri kazanılamaz.
Aşağıdaki şekil, daha yüksek bir hızda örneklendiğinde bir sinyali açıklar. 2w frekans alanında.
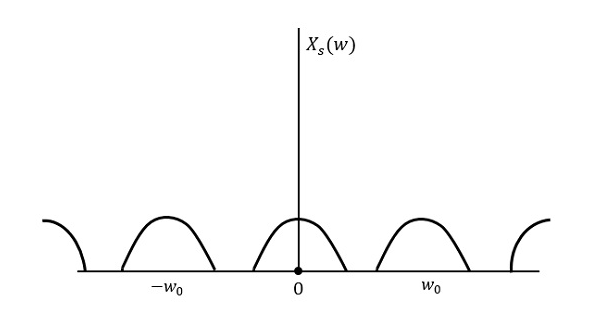
Yukarıdaki şekil bir sinyalin Fourier dönüşümünü göstermektedir $x_{s}(t)$. Burada bilgiler kayıpsız olarak çoğaltılır. Karıştırma yoktur ve dolayısıyla geri kazanım mümkündür.
Sinyalin Fourier Dönüşümü $x_{s}(t)$ dır-dir
$$ X_ {s} (w) = \ frac {1} {T_ {s}} \ sum_ {n = - \ infty} ^ \ infty X (w-nw_0) $$$ T_ {s} $ = nerede Sampling Period ve $ w_ {0} = \ frac {2 \ pi} {T_s} $
Örnekleme oranı, en yüksek frekansın iki katına eşitse ne olacağını görelim (2W)
Bunun anlamı,
$$ f_ {s} = 2W $$Nerede,
$ f_ {s} $ örnekleme sıklığıdır
W en yüksek frekans
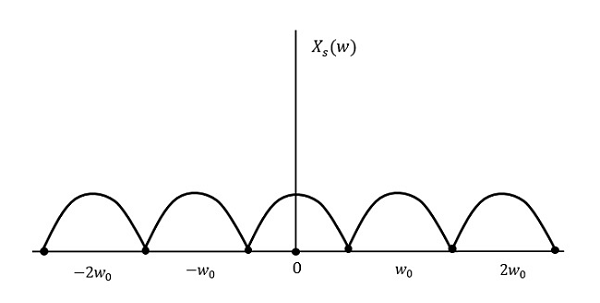
Sonuç, yukarıdaki şekilde gösterildiği gibi olacaktır. Bilgiler herhangi bir kayıp olmaksızın değiştirilir. Dolayısıyla, bu aynı zamanda iyi bir örnekleme oranıdır.
Şimdi duruma bakalım,
$$ f_ {s} <2W $$Ortaya çıkan desen aşağıdaki şekle benzeyecektir.

Yukarıdaki modelden, bilginin üst üste binmesinin yapıldığını ve bunun da bilgi kaybına ve karıştırmaya yol açtığını gözlemleyebiliriz. Bu istenmeyen üst üste binme olgusuna Aliasing adı verilir.
Aliasing
Takma ad, "örneklenmiş versiyonunun spektrumundaki düşük frekanslı bir bileşenin kimliğini alan, bir sinyalin spektrumundaki yüksek frekanslı bir bileşen olgusu" olarak adlandırılabilir.
Takma adın etkisini azaltmak için alınan düzeltici önlemler şunlardır:
PCM'nin verici bölümünde bir low pass anti-aliasing filter istenmeyen yüksek frekans bileşenlerini ortadan kaldırmak için örnekleyiciden önce kullanılır.
Filtrelemeden sonra örneklenen sinyal, Nyquist oranından biraz daha yüksek bir hızda örneklenir.
Nyquist oranından daha yüksek örnekleme oranına sahip olma seçeneği, aynı zamanda daha kolay tasarımına yardımcı olur. reconstruction filter alıcıda.
Fourier Dönüşümünün Kapsamı
Genel olarak, sinyallerin analizinde ve teoremlerin ispatlanmasında Fourier serileri ve Fourier dönüşümlerinden yardım aradığımız görülmektedir. Çünkü -
Fourier Dönüşümü, periyodik olmayan sinyaller için Fourier serisinin uzantısıdır.
Fourier dönüşümü, sinyalleri farklı alanlarda görüntülemeye yardımcı olan ve sinyalleri kolayca analiz etmeye yardımcı olan güçlü bir matematiksel araçtır.
Bu Fourier dönüşümü kullanılarak herhangi bir sinyal sinüs ve kosinüs toplamı cinsinden ayrıştırılabilir.
Bir sonraki bölümde, Niceleme kavramı hakkında tartışalım.