DSP - CT Sinyallerinin Sınıflandırılması
Sürekli zaman sinyalleri, sinyaller üzerinde gerçekleştirilen farklı koşullara veya işlemlere göre sınıflandırılabilir.
Çift ve Tek Sinyaller
Eşit Sinyal
Bir sinyalin aşağıdaki koşulu sağlasa bile olduğu söylenir;
$$ x (-t) = x (t) $$Sinyalin zamanın tersine çevrilmesi, burada genlikte herhangi bir değişiklik olduğu anlamına gelmez. Örneğin, aşağıda gösterilen üçgen dalgayı düşünün.
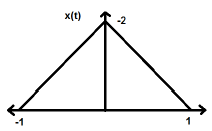
Üçgen sinyal, eşit bir sinyaldir. Zira Y ekseni etrafında simetriktir. Y ekseni ile ilgili ayna görüntüsü diyebiliriz.
Aşağıdaki şekilde gösterildiği gibi başka bir sinyali düşünün.
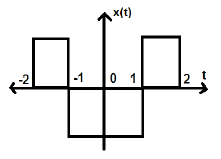
Yukarıdaki sinyalin, Y ekseni etrafında simetrik olduğu gibi bile olduğunu görebiliriz.
Garip Sinyal
Aşağıdaki koşulu yerine getiren bir sinyalin garip olduğu söylenir
$$ x (-t) = -x (t) $$Burada hem zamanın tersine çevrilmesi hem de genlik değişimi aynı anda gerçekleşir.
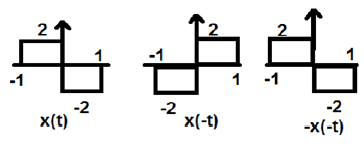
Yukarıdaki şekilde, x (t) adım sinyalini görebiliriz. Tek bir sinyal olup olmadığını test etmek için önce zamanı tersine çeviririz, yani x (-t) ve sonuç şekilde gösterildiği gibi olur. Sonra ortaya çıkan sinyalin genliğini, yani –x (-t) tersine çeviririz ve sonucu şekilde gösterildiği gibi alırız.
Birinci ve üçüncü dalga biçimini karşılaştırırsak, aynı olduklarını görebiliriz, yani kriterlerimizi karşılayan x (t) = -x (-t). Bu nedenle, yukarıdaki sinyal bir Odd sinyalidir.
Çift ve tek sinyallerle ilgili bazı önemli sonuçlar aşağıda verilmiştir.
- Çift × Çift = Çift
- Tek × Tek = Çift
- Çift × Tek = Tek
- Eşit ± Eşit = Eşit
- Tek ± Tek = Tek
- Çift ± Tek = Ne çift ne de tek
Herhangi bir sinyalin çift veya tek formda gösterimi
Bazı sinyaller doğrudan çift veya tek tip olarak sınıflandırılamaz. Bunlar hem çift hem de tek sinyalin bir kombinasyonu olarak temsil edilir.
$$ x (t) \ rightarrow x_ {e} (t) + x_ {0} (t) $$Burada x e (t) çift sinyali ve x o (t) tek sinyali temsil eder
$$ x_ {e} (t) = \ frac {[x (t) + x (-t)]} {2} $$Ve
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$Misal
$ X (n) = t + t ^ {2} + t ^ {3} $ sinyalinin çift ve tek kısımlarını bulun
Solution - x (n) 'yi ters çevirerek şunu elde ederiz
$$ x (-n) = -t + t ^ {2} -t ^ {3} $$
Şimdi, formüle göre, çift kısım
$$ x_ {e} (t) = \ frac {x (t) + x (-t)} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) + (- t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t ^ {2} $$
Benzer şekilde, formüle göre tek kısım
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) - (- t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t + t ^ {3} $$
Periyodik ve Periyodik Olmayan Sinyaller
Periyodik Sinyaller
Periyodik sinyal, belirli bir zaman aralığından sonra kendini tekrar eder. Bunu denklem formunda şu şekilde gösterebiliriz:
$$ x (t) = x (t) \ pm nT $$Nerede, n = bir tam sayı (1,2,3 ……)
T = Temel zaman periyodu (FTP) ≠ 0 ve ≠ ∞
Temel zaman periyodu (FTP), sinyalin periyodik olduğu en küçük pozitif ve sabit zaman değeridir.
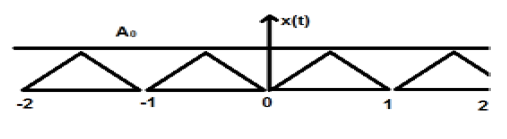
Yukarıdaki şekilde A genliğinin üçgen şeklinde bir sinyali gösterilmektedir. Burada sinyal her 1 saniyede bir tekrar etmektedir. Bu nedenle sinyalin periyodik ve FTP'sinin 1 sn olduğunu söyleyebiliriz.
Periyodik Olmayan Sinyal
Basitçe, periyodik olmayan sinyaller doğası gereği periyodik değildir diyebiliriz. Açıkça görüldüğü gibi, bu sinyaller herhangi bir aralık süresinden sonra kendilerini tekrar etmeyecektir.
Periyodik olmayan sinyaller belirli bir formatı takip etmez; bu nedenle, belirli bir matematiksel denklem onları tanımlayamaz.
Enerji ve Güç Sinyalleri
Bir sinyalin bir Enerji sinyali olduğu söylenir, ancak ve ancak, içerilen toplam enerji sonlu ve sıfır değilse (0 <E <∞). Bu nedenle, herhangi bir enerji tipi sinyal için, toplam normalleştirilmiş sinyal sonludur ve sıfır değildir.
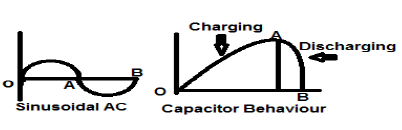
Sinüzoidal bir AC akım sinyali, Enerji tipi sinyalin mükemmel bir örneğidir çünkü bir durumda pozitif yarı döngüdedir ve sonraki yarım döngüde negatiftir. Bu nedenle, ortalama gücü sıfır olur.
Kayıpsız bir kapasitör aynı zamanda Enerji tipi sinyalin mükemmel bir örneğidir çünkü bir kaynağa bağlandığında optimum seviyesine kadar şarj olur ve kaynak kaldırıldığında, bu eşit miktarda enerjiyi bir yük yoluyla dağıtır ve ortalama gücünü sıfır.
Herhangi bir sonlu sinyal x (t) için enerji E olarak sembolize edilebilir ve şöyle yazılabilir;
$$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$Enerji tipi sinyallerin spektral yoğunluğu, çeşitli frekans seviyelerinde dağıtılan enerji miktarını verir.
Güç tipi Sinyaller
Bir sinyalin güç tipi sinyal olduğu söylenir, ancak ve ancak, normalleştirilmiş ortalama güç sonlu ve sıfır değildir, yani (0 <p <∞). Güç tipi sinyal için, normalleştirilmiş ortalama güç sonludur ve sıfır değildir. Neredeyse tüm periyodik sinyaller güç sinyalleridir ve ortalama güçleri sonludur ve sıfır değildir.
Matematiksel olarak bir x (t) sinyalinin gücü şu şekilde yazılabilir;
$$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$Enerji ve Güç Sinyalleri Arasındaki Fark
Aşağıdaki tablo Enerji ve Güç Sinyallerinin farklılıklarını özetlemektedir.
| Güç sinyali | Enerji Sinyali |
|---|---|
| Pratik periyodik sinyaller güç sinyalleridir. | Periyodik olmayan sinyaller enerji sinyalleridir. |
| Burada, Normalleştirilmiş ortalama güç sonludur ve sıfır değildir. | Burada toplam normalleştirilmiş enerji sonludur ve sıfır değildir. |
|
Matematiksel olarak, $$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$ |
Matematiksel olarak, $$ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $$ |
| Bu sinyallerin varlığı zamanla sonsuzdur. | Bu sinyaller sınırlı bir süre için mevcuttur. |
| Güç sinyalinin enerjisi sonsuz zaman boyunca sonsuzdur. | Enerji sinyalinin gücü sonsuz zaman boyunca sıfırdır. |
Çözülmüş Örnekler
Example 1 - $ z (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) + 4 \ sin (3 \ Pi + 30 ^ {o}) $ sinyalinin Gücünü bulun
Solution- Yukarıdaki iki sinyal birbirine diktir çünkü frekans terimleri birbiriyle aynıdır ve aynı faz farkına sahiptirler. Yani toplam güç, bireysel güçlerin toplamı olacaktır.
$ Z (t) = x (t) + y (t) $ olsun
$ X (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) $ ve $ y (t) = 4 \ sin (3 \ Pi + 30 ^ {o}) $
$ X (t) = \ frac {2 ^ {2}} {2} = 2 $ 'ın gücü
$ Y (t) = \ frac {4 ^ {2}} {2} = 8 $ 'ın gücü
Bu nedenle, $ P (z) = p (x) + p (y) = 2 + 8 = 10 $ … Ans.
Example 2 - $ x (t) = t ^ {2} + j \ sin t $ verilen sinyalin eşlenik olup olmadığını test edin.
Solution- Burada, t 2 olan gerçek kısım çift ve tek kısım (hayali) $ \ sin t $ olmak tektir. Yani yukarıdaki sinyal Eşlenik sinyalidir.
Example 3 - $ X (t) = \ sin \ omega t $ değerinin tek sinyal mi yoksa çift sinyal mi olduğunu doğrulayın.
Solution - $ X (t) = \ sin \ omega t $ verildiğinde
Zamanın tersine çevrilmesi ile, $ \ sin (- \ omega t) $ alacağız
Ancak $ \ sin (- \ phi) = - \ sin \ phi $ olduğunu biliyoruz.
Bu nedenle,
$$ \ sin (- \ omega t) = - \ sin \ omega t $$Bu, bir sinyalin tuhaf olması koşulunu tatmin ediyor. Bu nedenle, $ \ sin \ omega t $ tek bir sinyaldir.