Evrişim Teoremi
Son eğitimde, frekans alanındaki görüntüleri tartıştık. Bu eğitimde, frekans alanı ve görüntüler (uzamsal alan) arasında bir ilişki tanımlayacağız.
Örneğin
Bu örneği düşünün.

Frekans alanındaki aynı görüntü olarak temsil edilebilir.

Şimdi görüntü veya uzamsal alan ile frekans alanı arasındaki ilişki nedir? Bu ilişki Evrişim teoremi olarak adlandırılan bir teorem ile açıklanabilir.
Evrişim Teoremi
Uzamsal alan ile frekans alanı arasındaki ilişki, evrişim teoremi ile kurulabilir.
Evrişim teoremi olarak temsil edilebilir.
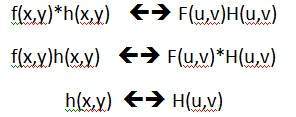
Uzamsal alandaki evrişim, frekans alanındaki filtrelemeye eşittir ve bunun tersi de ifade edilebilir.
Frekans alanındaki filtreleme şu şekilde temsil edilebilir:

The steps in filtering are given below.
İlk adımda, bir görüntüyü uzamsal alanda ön işlemden geçirmeliyiz, yani kontrastını veya parlaklığını artırmak
Sonra görüntünün ayrık Fourier dönüşümünü alacağız
Daha sonra ayrık Fourier dönüşümünü köşelerden merkeze getireceğimiz için ayrık Fourier dönüşümünü ortalayacağız.
Sonra filtreleme uygulayacağız, yani Fourier dönüşümünü bir filtre fonksiyonu ile çarpacağız.
Ardından DFT'yi tekrar merkezden köşelere kaydıracağız
Son adım, sonucu frekans alanından uzamsal alana geri getirmek için ayrık Fourier dönüşümünü tersine çevirmek olacaktır.
Ve bu son işlem adımı isteğe bağlıdır, tıpkı ön işleme gibi, sadece görüntünün görünümünü artırdığımız.
Filtreler
Frekans alanındaki filtre kavramı, evrişimdeki maske kavramı ile aynıdır.
Bir görüntüyü frekans alanına dönüştürdükten sonra, bir görüntü üzerinde farklı türde işlemler gerçekleştirmek için filtreleme işleminde bazı filtreler uygulanır. İşleme, bir görüntüyü bulanıklaştırma, bir görüntüyü keskinleştirme vb. İçerir.
Bu amaçlara yönelik yaygın filtre türleri şunlardır:
- İdeal yüksek geçiş filtresi
- İdeal düşük geçiş filtresi
- Gauss yüksek geçiren filtre
- Gauss düşük geçiş filtresi
Bir sonraki eğitimde, filtre hakkında ayrıntılı olarak tartışacağız.