Fourier Serileri ve Dönüşümü

Frekans alanı analizinin son eğitiminde, Fourier serisinin ve Fourier dönüşümünün bir sinyali frekans alanına dönüştürmek için kullanıldığını tartıştık.

Fourier

Fourier, 1822'de bir matematikçiydi. Bir sinyali frekans alanına dönüştürmek için Fourier serilerini ve Fourier dönüşümünü verdi.

Fourier Serisi

Fourier serisi basitçe, periyodik sinyallerin belirli bir ağırlık ile çarpıldığında sinüs ve kosinüs toplamı olarak temsil edilebileceğini ve ayrıca periyodik sinyallerin aşağıdaki özelliklerle başka sinyallere bölünebileceğini belirtir.

Sinyaller sinüsler ve kosinüslerdir
Sinyaller birbirinin harmonikleridir

Resimsel olarak şu şekilde görüntülenebilir:

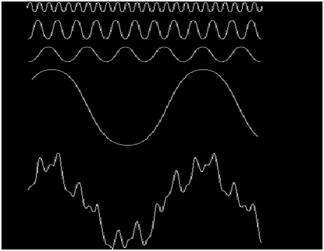
Yukarıdaki sinyalde, son sinyal aslında yukarıdaki tüm sinyallerin toplamıdır. Fourier fikri buydu.

Nasıl hesaplanır

Frekans alanında gördüğümüz gibi, bir görüntüyü frekans alanında işlemek için önce onu kullanarak onu frekans alanına dönüştürmemiz ve çıktının tersini alıp uzaysal alana dönüştürmemiz gerekir. Bu nedenle hem Fourier serisinin hem de Fourier dönüşümünün iki formülü vardır. Biri dönüştürme ve diğeri onu uzamsal alana geri dönüştürme için.

Fourier serisi

Fourier serisi bu formülle gösterilebilir.

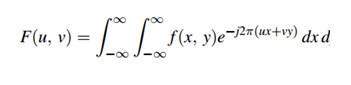
Tersi bu formülle hesaplanabilir.

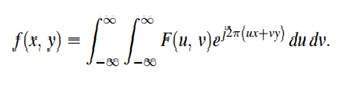
Fourier dönüşümü

Fourier dönüşümü basitçe, eğrinin altındaki alanı sonlu olan periyodik olmayan sinyallerin, belirli bir ağırlıkla çarpıldıktan sonra sinüslerin ve kosinüslerin integralleri olarak da temsil edilebileceğini belirtir.

Fourier dönüşümü, görüntü sıkıştırma (örn. JPEG sıkıştırma), filtreleme ve görüntü analizi gibi birçok geniş uygulamaya sahiptir.

Fourier serisi ve dönüşümü arasındaki fark

Hem Fourier serisi hem de Fourier dönüşümü Fourier tarafından verilmesine rağmen, aralarındaki fark Fourier serisinin periyodik sinyallere ve Fourier dönüşümünün periyodik olmayan sinyaller için uygulandığı

Görüntülere hangisi uygulanır

Şimdi soru, hangisinin görüntülere, Fourier serisine veya Fourier dönüşümüne uygulandığıdır. Bu sorunun cevabı, görüntülerin ne olduğu gerçeğinde yatmaktadır. Görüntüler periyodik değildir. Ve görüntüler periyodik olmadığından, onları frekans alanına dönüştürmek için Fourier dönüşümü kullanılır.

Ayrık fourier dönüşümü

Görüntülerle ve aslında dijital görüntülerle uğraştığımız için, dijital görüntüler için ayrı fourier dönüşümü üzerinde çalışacağız.

Bir sinüzoidin yukarıdaki Fourier terimini düşünün. Üç şey içerir.

Mekansal frekans
Magnitude
Phase

Uzamsal frekans, doğrudan görüntünün parlaklığı ile ilişkilidir. Sinüzoidin büyüklüğü doğrudan kontrastla ilişkilidir. Kontrast, maksimum ve minimum piksel yoğunluğu arasındaki farktır. Faz, renk bilgilerini içerir.

2 boyutlu ayrık Fourier dönüşümü için formül aşağıda verilmiştir.

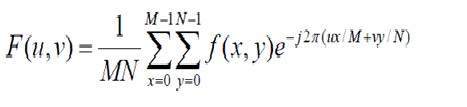
Ayrık Fourier dönüşümü aslında örneklenmiş Fourier dönüşümüdür, bu nedenle bir görüntüyü belirten bazı örnekler içerir. Yukarıdaki formülde f (x, y) görüntüyü belirtir ve F (u, v) ayrı Fourier dönüşümünü belirtir. 2 boyutlu ters ayrık Fourier dönüşümü için formül aşağıda verilmiştir.

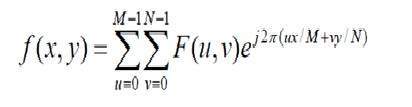
Ters ayrık Fourier dönüşümü, Fourier dönüşümünü tekrar görüntüye dönüştürür

Bu sinyali düşünün

Şimdi, FFT büyüklük spektrumunu hesaplayacağımız ve sonra FFT büyüklük spektrumunu değiştireceğimiz bir görüntü göreceğiz ve sonra bu değişen spektrumun Log'unu alacağız.