Hızlı rehber

Herhangi bir miktarı ölçmek için kullanılan aletler ölçü aletleri olarak bilinir. Bu eğitim esas olarak şu konuları kapsar:electronic instrumentselektriksel büyüklükleri veya parametreleri ölçmek için kullanışlıdır.

Aşağıdakiler en yaygın kullanılan elektronik aletlerdir.

• Voltmeter
• Ammeter
• Ohmmeter
• Multimeter

Şimdi kısaca bu enstrümanlar hakkında konuşalım.

Voltmetre

Adından da anlaşılacağı gibi, voltmeterbir elektrik devresinin herhangi iki noktasındaki voltajı ölçen bir ölçüm cihazıdır. İki tip voltmetre vardır: DC voltmetre ve AC voltmetre.

DC voltmetre, bir elektrik devresinin herhangi iki noktasındaki DC voltajını ölçerken, AC voltmetre, bir elektrik devresinin herhangi iki noktasındaki AC voltajını ölçer. Bir örnekpractical DC voltmeter aşağıdaki şekilde gösterilmiştir.

Yukarıdaki şekilde gösterilen DC voltmetre bir $(0-100)V$ DC voltmeter. Bu nedenle sıfır volttan 10 volta kadar olan DC gerilimleri ölçmek için kullanılabilir.

Ampermetre

Adından da anlaşılacağı gibi, ammeterbir elektrik devresinin herhangi iki noktasından geçen akımı ölçen bir ölçüm aletidir. İki tür ampermetre vardır: DC ampermetre ve AC ampermetre.

DC ampermetre, bir elektrik devresinin herhangi iki noktasından geçen DC akımını ölçer. Oysa AC ampermetre, bir elektrik devresinin herhangi iki noktasından geçen AC akımını ölçer. Bir örnekpractical AC ammeter aşağıdaki şekilde gösterilmiştir -

Yukarıdaki şekilde gösterilen AC ampermetre bir $(0-100)A \:$ AC ammeter. Bu nedenle, sıfır Amperden 100 Amper'e kadar AC akımlarını ölçmek için kullanılabilir.

Ohmmetre

Ohmmeterbir elektrik devresinin herhangi iki noktası arasındaki direncin değerini ölçmek için kullanılır. Bilinmeyen bir direncin değerini bulmak için de kullanılabilir. İki tür ohmmetre vardır: seri ohmmetre ve şönt ohmmetre.

Seri tip ohmmetrede, değeri bilinmeyen ve ölçülecek olan direnç, ohmmetre ile seri bağlanmalıdır. Ölçmek için kullanışlıdırhigh values of resistances.

Şönt tipi ohmmetrede değeri bilinmeyen ve ölçülecek direnç, ohmmetre ile paralel (şönt) bağlanmalıdır. Ölçmek için kullanışlıdırlow values of resistances.

Bir örnek practical shunt ohmmeteryukarıdaki şekilde gösterilmiştir. Yukarıdaki şekilde gösterilen ohmmetre bir$(0-100)\Omega$ shunt ohmmeter. Dolayısıyla sıfır ohm'dan 100 ohm'a kadar direnç değerlerini ölçmek için kullanılabilir.

Multimetre

Multimetergerilim, akım ve direnç gibi büyüklükleri birer birer ölçmek için kullanılan elektronik bir araçtır. DC ve AC voltajlarını, DC ve AC akımlarını ve çeşitli aralıklardaki dirençleri ölçmek için kullanılabilir. Aşağıdaki şekilde pratik bir multimetre gösterilmektedir -

Şekilde gösterildiği gibi, bu multimetre çeşitli yüksek dirençleri, düşük dirençleri, DC voltajlarını, AC voltajlarını, DC akımlarını ve AC akımlarını ölçmek için kullanılabilir. Bu miktarların her biri için farklı ölçekler ve değer aralıkları yukarıdaki şekilde işaretlenmiştir.

Bu bölümde ele aldığımız araçlar, indicating type instruments, bu enstrümanların işaretçileri belirli bir değeri saptırıp işaret ederken. Daha sonraki bölümlerde bu elektronik ölçü aletlerini detaylı olarak tartışacağız.

Enstrümanın performansını bilmeye yardımcı olan ve herhangi bir miktar veya parametrenin ölçülmesine yardımcı olan ölçüm enstrümanlarının özellikleri, Performance Characteristics.

Performans Özelliklerinin Türleri

Aletlerin performans özellikleri aşağıdaki şekilde sınıflandırılabilir: two types.

• Statik Özellikler
• Dinamik Özellikler

Şimdi bu iki tür özelliği tek tek tartışalım.

Statik Özellikler

Miktar veya parametre ölçüm cihazlarının özellikleri do not varyzamana göre statik özellikler denir. Bazen bu miktarlar veya parametreler zamana göre yavaşça değişebilir. Listesi aşağıdadırstatic characteristics.

• Accuracy
• Precision
• Sensitivity
• Resolution
• Statik Hata

Şimdi bu statik özellikleri tek tek tartışalım.

Doğruluk

Bir enstrümanın belirtilen değeri olan $ A_ {i} $ ile gerçek değer $ A_ {t} $ arasındaki cebirsel fark şu şekilde bilinir: accuracy. Matematiksel olarak şu şekilde temsil edilebilir -

$$ Doğruluk = A_ {i} - A_ {t} $$

Doğruluk terimi, bir enstrümanın belirtilen değerinin, $ A_ {i} $, gerçek değer olan $ A_ {t} $ değerine ne kadar yakın olduğunu belirtir.

Statik Hata

Gerçek değer, zamana göre değişmeyen miktarın $ A_ {t} $ ile bir enstrümanın belirtilen değeri arasındaki fark, $ A_ {i} $ olarak bilinir static error, $ e_ {s} $. Matematiksel olarak şu şekilde temsil edilebilir -

$$ e_ {s} = A_ {t} - A_ {i} $$

Statik hata terimi, enstrümanın yanlışlığını ifade eder. Statik hata yüzde cinsinden ifade edilirse, o zaman denirpercentage of static error. Matematiksel olarak şu şekilde temsil edilebilir -

$$ \% e_ {s} = \ frac {e_ {s}} {A_ {t}} \ times 100 $$

Bunun yerine, yukarıdaki denklemin sağ tarafındaki $ e_ {s} $ değerini -

$$ \% e_ {s} = \ frac {A_ {t} - A_ {i}} {A_ {t}} \ times 100 $$

Nerede,

$ \% e_ {s} $, statik hatanın yüzdesidir.

Hassas

Bir enstrüman aynı miktarı aynı koşullarda ve herhangi bir sayıda ölçmek için kullanıldığında tekrar tekrar aynı değeri gösteriyorsa, enstrümanın yüksek olduğunu söyleyebiliriz. precision.

Duyarlılık

Çıktıdaki değişim oranı, girdideki belirli bir değişiklik için bir enstrümanın $ \ Delta A_ {out} $, ölçülecek olan $ \ Delta A_ {in} $ olarak adlandırılır sensitivity, S. Matematiksel olarak şu şekilde temsil edilebilir -

$$ S = \ frac {\ Delta A_ {dışarı}} {\ Delta A_ {in}} $$

Terimi duyarlılık yanıt verdiklerini bir araç için gerekli olan ölçülebilir girdi en küçük bir değişiklik anlamına gelir.

• Kalibrasyon eğrisi ise linear, bu durumda aletin hassasiyeti sabit olacaktır ve kalibrasyon eğrisinin eğimine eşittir.

• Kalibrasyon eğrisi ise non-linear, bu durumda enstrümanın hassasiyeti sabit olmayacak ve girişe göre değişecektir.

çözüm

Bir enstrümanın çıkışı yalnızca girişte belirli bir artış olduğunda değişecekse, o zaman girişin bu artışı çağrılır Resolution. Bu, girdi çözünürlüğü olduğunda enstrümanın girdiyi etkili bir şekilde ölçebildiği anlamına gelir.

Dinamik Özellikler

Zamana göre çok hızlı değişen miktarları veya parametreleri ölçmek için kullanılan enstrümanların özelliklerine dinamik özellikler denir. Listesi aşağıdadırdynamic characteristics.

• Cevap hızı
• Dinamik Hata
• Fidelity
• Lag

Şimdi bu dinamik özellikleri tek tek tartışalım.

Cevap hızı

Ölçülecek miktarda herhangi bir değişiklik olduğunda aletin tepki verdiği hız denir. speed of response. Enstrümanın ne kadar hızlı olduğunu gösterir.

Gecikme

Ölçülecek miktarda bir değişiklik olduğunda, bir aletin tepkisinde mevcut olan gecikme miktarına ölçüm gecikmesi denir. Aynı zamanda basitçelag.

Dinamik Hata

Gerçek değer, zamana göre değişen miktarın $ A_ {t} $ ile bir enstrümanın belirtilen değeri arasındaki fark, $ A_ {i} $ dinamik hata, $ e_ {d} $ olarak bilinir.

Sadakat

Bir aletin ölçülen miktardaki değişiklikleri dinamik bir hata olmadan gösterme derecesi olarak bilinir. Fidelity

Ölçüm sırasında oluşan hatalar şu şekilde bilinir: measurement errors. Bu bölümde, ölçüm hatalarının türlerini tartışalım.

Ölçüm Hatası Türleri

Ölçüm hatalarını aşağıdaki üç türe ayırabiliriz.

• Brüt Hatalar
• Rastgele Hatalar
• Sistematik Hatalar

Şimdi bu üç tür ölçüm hatasını tek tek tartışalım.

Brüt Hatalar

Gözlemcinin ölçüm değerlerini alırken deneyimsizliğinden dolayı oluşan hatalar, gross errors. Büyük hataların değerleri gözlemciden gözlemciye değişecektir. Bazen, cihazın yanlış seçilmesi nedeniyle büyük hatalar da meydana gelebilir. Bu iki adımı izleyerek büyük hataları en aza indirebiliriz.

• Ölçülecek değer aralığına bağlı olarak en uygun cihazı seçin.
• Okumaları dikkatlice not edin

Sistematik Hatalar

Cihaz, çalışması sırasında sabit bir tekdüze sapmaya sahip bir hata üretirse, systematic error. Cihazda kullanılan malzemelerin özelliklerinden dolayı sistematik hatalar oluşur.

Types of Systematic Errors

Sistematik hatalar aşağıdaki şekilde sınıflandırılabilir: three types.

• Instrumental Errors - Bu tür hatalar, aletlerin eksiklikleri ve yükleme etkileri nedeniyle oluşur.

• Environmental Errors - Bu tür hatalar sıcaklık, basınç vb. Değişimler gibi ortamdaki değişiklikler nedeniyle oluşur.

• observational Errors - Bu tip hatalar gözlemciden sayaç okumaları alırken meydana gelir. Parallax errors bu tür hatalara aittir.

Rastgele Hatalar

Ölçüm sırasında bilinmeyen kaynaklardan kaynaklanan hatalar, random errors. Dolayısıyla bu hataları ortadan kaldırmak veya en aza indirmek mümkün değildir. Ancak rastgele hatasız daha doğru ölçüm değerleri elde etmek istiyorsak, bu iki adımı takip ederek mümkündür.

• Step1 - Farklı gözlemcilerden daha fazla sayıda okuma alın.

• Step2 - 1. Adımda elde edilen okumalar üzerinde istatistiksel analiz yapın.

İstatistiksel analizde kullanılan parametreler aşağıdadır.

• Mean
• Median
• Variance
• Deviation
• Standart sapma

Şimdi bunları tartışalım statistical parameters.

Anlamına gelmek

$ X_ {1}, x_ {2}, x_ {3}, ...., x_ {N} $ belirli bir ölçümün $ N $ okumaları olsun. Ortalama veyaaverage value Bu değerlerin% 'si aşağıdaki formül kullanılarak hesaplanabilir.

$$ m = \ frac {x_ {1} + x_ {2} + x_ {3} + .... + x_ {N}} {N} $$

Burada, $ m $ ortalama veya ortalama değerdir.

Belirli bir ölçümün okuma sayısı daha fazlaysa, ortalama veya ortalama değer yaklaşık olarak eşit olacaktır. true value

Medyan

Belirli bir ölçümün okuma sayısı daha fazlaysa, ortalama veya ortalama değeri hesaplamak zordur. Burada hesaplayınmedian value ve yaklaşık olarak ortalama değere eşit olacaktır.

Medyan değeri hesaplamak için, önce belirli bir ölçümün okumalarını bir ascending order. Medyan değeri aşağıdaki formülü kullanarak hesaplayabiliriz, okuma sayısı birodd number.

$$ M = x _ {\ left (\ frac {N + 1} {2} \ right)} $$

Medyan değeri aşağıdaki formülü kullanarak hesaplayabiliriz, okuma sayısı bir even number.

$$ M = \ frac {x _ {\ left (N / 2 \ right)} + x_ \ left (\ sol [N / 2 \ sağ] +1 \ sağ)} {2} $$

Ortalamadan Sapma

Belirli bir ölçümün okunması ile ortalama değer arasındaki fark, ortalamadan sapma olarak bilinir . Kısaca buna sapma denir . Matematiksel olarak şu şekilde temsil edilebilir:

$$ d_ {i} = x_ {i} -m $$

Nerede,

$ d_ {i} $, $ i ^ {th} $ okumasının ortalamadan sapmasıdır.

$ x_ {i} $, $ i ^ {th} $ okuma değeridir.

$ m $ ortalama veya ortalama değerdir.

Standart sapma

Kök ortalama sapma karesine denir standard deviation. Matematiksel olarak şu şekilde temsil edilebilir:

$$ \ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { d_ {N}} ^ {2}} {N}} $$

Yukarıdaki formül, okuma sayısı N 20'den büyük veya eşitse geçerlidir. Okuma sayısı N 20'den az olduğunda standart sapma için aşağıdaki formülü kullanabiliriz.

$$ \ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { d_ {N}} ^ {2}} {N-1}} $$

Nerede,

$ \ sigma $ standart sapmadır

$ d_ {1}, d_ {2}, d_ {3},…, d_ {N} $ sırasıyla birinci, ikinci, üçüncü,…, $ N ^ {th} $ okumalarının ortalamadan sapmalarıdır.

Note - Standart sapmanın değeri küçükse, ölçümün okuma değerlerinde daha fazla doğruluk olacaktır.

Varyans

Standart sapmanın karesine denir variance. Matematiksel olarak şu şekilde temsil edilebilir:

$$ V = \ sigma ^ {2} $$

Nerede,

$ V $ varyans

$ \ sigma $ standart sapmadır

Ortalama sapma karesi de denir variance. Matematiksel olarak şu şekilde temsil edilebilir:

$$ V = \ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + {d_ {N} } ^ {2}} {N} $$

Yukarıdaki formül, okuma sayısı N 20'den büyük veya eşitse geçerlidir. Okuma sayısı, N 20'den az olduğunda varyans için aşağıdaki formülü kullanabiliriz.

$$ V = \ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + {d_ {N} } ^ {2}} {N-1} $$

Nerede,

$ V $ varyans

$ d_ {1}, d_ {2}, d_ {3},…, d_ {N} $ sırasıyla birinci, ikinci, üçüncü,…, $ N ^ {th} $ okumalarının ortalamadan sapmalarıdır.

Böylece, istatistiksel parametrelerin yardımıyla, belirli bir ölçümün okumalarını analiz edebiliriz. Bu sayede daha doğru ölçüm değerleri elde edeceğiz.

Herhangi bir miktarı ölçmek için kullanılan aletler olarak bilinir measuring instruments. Aletler, voltaj ve akım gibi temel elektriksel büyüklükleri ölçebiliyorsa,basic measuring instruments.

Temel Ölçü Aletleri Türleri

Temel ölçü aletlerini aşağıdaki iki türe sınıflandırabiliriz.

• Voltmeters
• Ammeters

Bu iki temel ölçü aletini kısaca tartışalım.

Voltmetreler

Adından da anlaşılacağı gibi, voltmeterbir elektrik devresinin herhangi iki noktasındaki voltajı ölçen bir ölçüm cihazıdır. Voltaj birimleri volt ve ölçüm cihazı metredir. Bu nedenle, "voltmetre" kelimesi iki kelimenin birleştirilmesiyle elde edilir.“volt” ve “meter”.

Voltmetreleri aşağıdaki şekilde sınıflandırabiliriz two types ölçebileceği voltaj türüne göre.

• DC Voltmetreler
• AC Voltmetreler

DC Voltmetre

Adından da anlaşılacağı gibi, DC voltmetre DC voltagebir elektrik devresinin herhangi iki noktası arasında. Aşağıdaki şekilde pratik bir DC voltmetre gösterilmektedir.

Şekilde gösterilen DC voltmetre bir $(0-10)V$ DC voltmeter. Bu nedenle sıfır volttan 10 volta kadar olan DC voltajlarını ölçmek için kullanılabilir.

AC Voltmetre

Adından da anlaşılacağı gibi, AC voltmetre AC voltagebir elektrik devresinin herhangi iki noktası arasında. Aşağıdaki şekilde pratik bir AC voltmetre gösterilmektedir.

Yukarıdaki şekilde gösterilen AC voltmetre bir $(0-250)V$ AC voltmeter. Bu nedenle sıfır volttan 250 volta kadar AC voltajlarını ölçmek için kullanılabilir.

Ampermetreler

Adından da anlaşılacağı gibi, ammeterbir elektrik devresinin herhangi iki noktasından geçen akımı ölçen bir ölçüm aletidir. Akım birimi amperdir ve ölçü aleti metredir. "Ampermetre" kelimesi birleştirilerek elde edilir.“am” amper ile “meter”.

Ampermetreleri aşağıdaki şekilde sınıflandırabiliriz two types ölçebileceği akım türüne göre.

• DC Ampermetreler
• AC Ampermetreler

DC Ampermetre

Adından da anlaşılacağı gibi, DC ampermetre, DC currentbir elektrik devresinin herhangi iki noktasından akar. Pratik bir DC ampermetre şekilde gösterilmiştir.

Yukarıdaki şekilde gösterilen DC ampermetre bir $(0-50)A$ DC ammeter. Bu nedenle, DC akımlarını sıfır Amperden 50 Amper'e kadar ölçmek için kullanılabilir.

AC Ampermetre

Adından da anlaşılacağı gibi, AC ampermetre, AC currentbir elektrik devresinin herhangi iki noktasından akar. Pratik bir AC ampermetre aşağıdaki şekilde gösterilmiştir.

Yukarıdaki şekilde gösterilen AC ampermetre bir $(0-100)A$ AC ammeter. Bu nedenle, sıfır Amperden 100 Amper'e kadar AC akımlarını ölçmek için kullanılabilir.

Aşağıdaki birkaç bölümde çeşitli voltmetreler ve ampermetreler hakkında ayrıntılı olarak tartışacağız.

DC voltmetre, herhangi iki elektrik devresi noktasındaki DC voltajını ölçmek için kullanılan bir ölçüm cihazıdır. Kalıcı Mıknatıslı Hareketli Bobin (PMMC) galvanometre ile seri olarak bir direnç yerleştirirsek, tüm kombinasyon birlikteDC voltmeter.

DC voltmetrede kullanılan seri direnç, seri çarpan direnci veya basitçe çarpan olarak da adlandırılır. Temel olarak, sayaç akımının tam ölçek sapma değerini aşmasını önlemek için galvanometreden geçen akım miktarını sınırlar. circuit diagram DC voltmetre aşağıdaki şekilde gösterilmiştir.

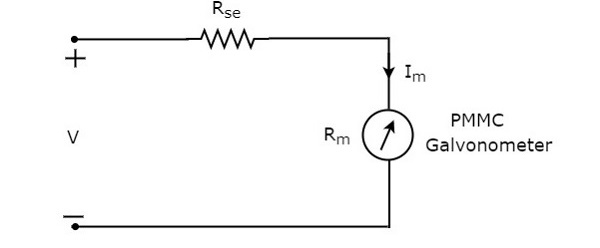
Bu DC voltmetreyi, DC voltajının ölçülecek olduğu bir elektrik devresinin iki noktasına yerleştirmeliyiz.

Uygulamak KVL yukarıdaki devrenin döngüsü etrafında.

$ V-I_ {m} R_ {se} -I_ {m} R_ {m} = 0 $ (Denklem 1)

$$ \ Rightarrow V-I_ {m} R_ {m} = I_ {m} R_ {se} $$

$$ \ Rightarrow R_ {se} = \ frac {V-I_ {m} R_ {m}} {I_ {m}} $$

$ \ Rightarrow R_ {se} = \ frac {V} {I_ {m}} - R_ {m} $ (Denklem 2)

Nerede,

$ R_ {se} $, seri çarpan direncidir

$ V $ ölçülecek tam DC voltaj aralığıdır

$ I_ {m} $ tam ölçekli sapma akımıdır

$ R_ {m} $ galvanometrenin iç direncidir

Ölçülecek tam aralıklı DC voltajı, $ V $ ve galvanometre boyunca DC voltaj düşüşü, $ V_ {m} $ olarak bilinir. multiplying factor, m. Matematiksel olarak şu şekilde temsil edilebilir:

$ m = \ frac {V} {V_ {m}} $ (Denklem 3)

Denklem 1'den aşağıdaki denklemi alacağız full range DC voltage bu ölçülecek, $ V $.

$ V = I_ {m} R_ {se} + I_ {m} R_ {m} $ (Denklem 4)

DC voltage dropgalvanometre boyunca, $ V_ {m} $ tam ölçekli sapma akımının, $ I_ {m} $ ve galvanometrenin iç direncinin, $ R_ {m} $ çarpımıdır. Matematiksel olarak şu şekilde yazılabilir:

$ V_ {m} = I_ {m} R_ {m} $ (Denklem 5)

SubstituteDenklem 3'teki Denklem 4 ve Denklem 5.

$$ m = \ frac {I_ {m} R_ {se} + I_ {m} R_ {m}} {I_ {m} R_ {m}} $$

$ \ Rightarrow m = \ frac {R_ {se}} {R_ {m}} + 1 $

$ \ Rightarrow m-1 = \ frac {R_ {se}} {R_ {m}} $

$ R_ {se} = R_ {m} \ left (m-1 \ right) $ (Denklem 6)

Bulabiliriz value of series multiplier resistance Mevcut verilere göre Denklem 2 veya Denklem 6'yı kullanarak.

Çok Aralıklı DC Voltmetre

Önceki bölümde, PMMC galvanometre ile seri olarak bir çarpan direnci yerleştirilerek elde edilen DC voltmetreyi tartışmıştık. Bu DC voltmetre, ölçmek için kullanılabilir.particular range DC voltajları.

DC voltmetreyi DC voltajlarını ölçmek için kullanmak istiyorsak multiple ranges, o zaman tek çarpan direnci yerine birden çok paralel çarpan direnci kullanmalıyız ve bu direnç kombinasyonunun tamamı PMMC galvanometre ile seri halindedir. circuit diagram Çok aralıklı DC voltmetre aşağıdaki şekilde gösterilmiştir.

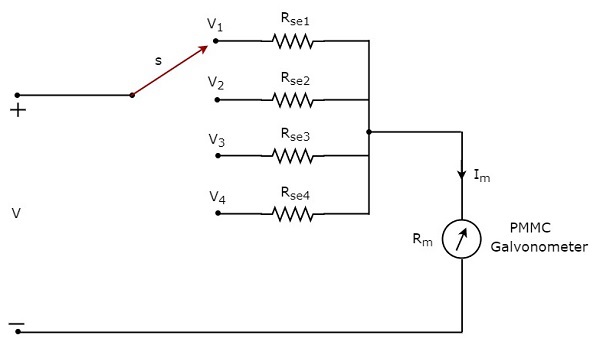
Bunu yerleştirmeliyiz multi range DC voltmetergerekli aralıktaki DC voltajının ölçülecek olduğu bir elektrik devresinin iki noktası boyunca. Anahtarları ilgili çarpan direncine bağlayarak istenen voltaj aralığını seçebiliriz.

$ M_ {1}, m_ {2}, m_ {2} $ ve $ m_ {4} $ multiplying factorsDC voltmetrenin tam aralıktaki DC gerilimlerinin sırasıyla $ V_ {1}, V_ {2}, V_ {3} $ ve $ V_ {4} $ olarak ölçüldüğünü düşündüğümüzde Her çarpan faktöre karşılık gelen formüller aşağıdadır.

$$ m_ {1} = \ frac {V_ {1}} {V_ {m}} $$

$$ m_ {2} = \ frac {V_ {2}} {V_ {m}} $$

$$ m_ {3} = \ frac {V_ {3}} {V_ {m}} $$

$$ m_ {4} = \ frac {V_ {4}} {V_ {m}} $$

Yukarıdaki devrede, dört series multiplier resistors$ R_ {se1}, R_ {se2}, R_ {se3} $ ve $ R_ {se4} $. Bu dört dirence karşılık gelen formüller aşağıdadır.

$$ R_ {se1} = R_ {m} \ sol (m_ {1} -1 \ sağ) $$

$$ R_ {se2} = R_ {m} \ sol (m_ {2} -1 \ sağ) $$

$$ R_ {se3} = R_ {m} \ sol (m_ {3} -1 \ sağ) $$

$$ R_ {se4} = R_ {m} \ sol (m_ {4} -1 \ sağ) $$

Dolayısıyla, yukarıdaki formülleri kullanarak her seri çarpan direncinin direnç değerlerini bulabiliriz.

Herhangi iki elektrik devresi noktasındaki AC voltajını ölçmek için kullanılan cihaza denir. AC voltmeter. AC voltmetre redresörden oluşuyorsa, redresör bazlı AC voltmetre olduğu söylenir.

DC voltmetre yalnızca DC voltajlarını ölçer. Bunu AC voltajlarını ölçmek için kullanmak istiyorsak, bu iki adımı izlemeliyiz.

• Step1 - Bir redresör kullanarak AC voltaj sinyalini DC voltaj sinyaline dönüştürün.

• Step2 - Doğrultucunun çıkış sinyalinin DC veya ortalama değerini ölçün.

Biz alırız Rectifier based AC voltmeter, sadece doğrultucu devresini temel DC voltmetreye dahil ederek. Bu bölüm doğrultucu tabanlı AC voltmetreler ile ilgilidir.

Doğrultucu tabanlı AC Voltmetre Türleri

Aşağıdakiler two types doğrultucu tabanlı AC voltmetreler.

• Yarım Dalga Doğrultucu kullanan AC voltmetre
• Tam Dalga Doğrultucu kullanan AC voltmetre

Şimdi bu iki AC voltmetreyi tek tek tartışalım.

Yarım Dalga Doğrultucu kullanan AC Voltmetre

DC voltmetrenin önüne bir Yarım dalga doğrultucu bağlanırsa, bu kombinasyonun tamamına Yarım dalga doğrultucu kullanan AC voltmetre denir. block diagram Yarım dalga doğrultucu kullanan AC voltmetre aşağıdaki şekilde gösterilmiştir.

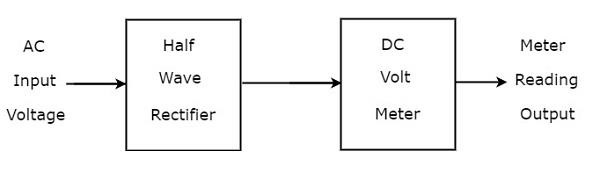
Yukarıdaki blok diyagram iki bloktan oluşur: yarım dalga doğrultucu ve DC voltmetre. Sadece her bloğu yukarıdaki blok diyagramındaki ilgili bileşen (ler) ile değiştirerek ilgili devre şemasını alacağız. Böylececircuit diagram Yarım dalga doğrultucu kullanan AC voltmetre, aşağıdaki şekilde gösterildiği gibi görünecektir.

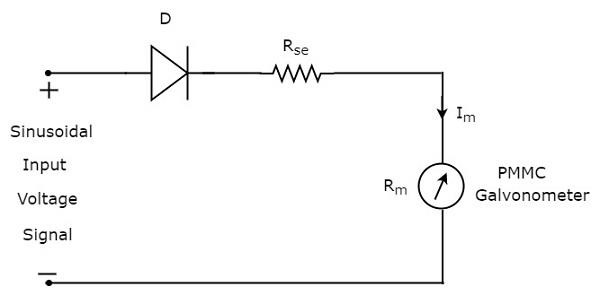
rms value sinüzoidal (AC) giriş voltajı sinyalinin

$$ V_ {rms} = \ frac {V_ {m}} {\ sqrt {2}} $$

$$ \ Rightarrow V_ {m} = \ sqrt {2} V_ {rms} $$

$$ \ Rightarrow V_ {m} = 1.414 V_ {rms} $$

Nerede,

$ V_ {m} $, sinüzoidal (AC) giriş voltajı sinyalinin maksimum değeridir.

DC veya Yarım dalga doğrultucunun çıkış sinyalinin ortalama değeri

$$ V_ {dc} = \ frac {V_ {m}} {\ pi} $$

Substitute, yukarıdaki denklemdeki $ V_ {m} $ değeri.

$$ V_ {dc} = \ frac {1.414 V_ {rms}} {\ pi} $$

$$ V_ {dc} = 0,45 V_ {rms} $$

Bu nedenle, AC voltmetre şuna eşit bir çıkış voltajı üretir. 0.45 sinüzoidal (AC) giriş voltajı sinyalinin rms değerinin katı

Tam Dalga Doğrultucu kullanan AC Voltmetre

DC voltmetrenin önüne bir Tam dalga doğrultucu bağlanırsa, bu kombinasyonun tamamına Tam dalga doğrultucu kullanan AC voltmetre denir. block diagram Tam dalga doğrultucu kullanan AC voltmetre aşağıdaki şekilde gösterilmiştir

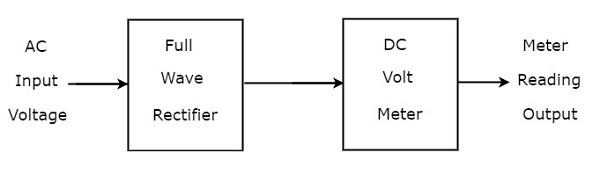
Yukarıdaki blok şeması iki bloktan oluşur: tam dalga doğrultucu ve DC voltmetre. Karşılık gelen devre şemasını sadece her bloğu yukarıdaki blok şemasındaki ilgili bileşen (ler) ile değiştirerek elde edeceğiz.

Böylece circuit diagram Tam dalga doğrultucu kullanan AC voltmetre, aşağıdaki şekilde gösterildiği gibi görünecektir.

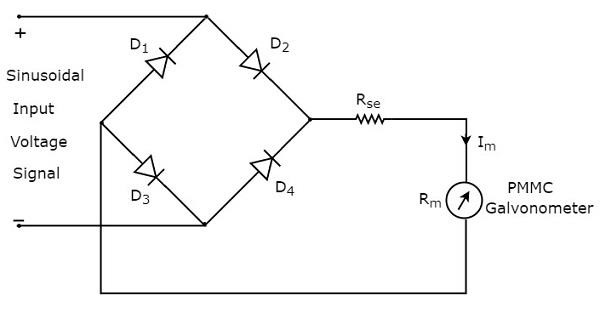
rms value sinüzoidal (AC) giriş voltajı sinyalinin

$$ V_ {rms} = \ frac {V_ {m}} {\ sqrt {2}} $$

$$ \ Rightarrow V_ {m} = \ sqrt {2} \: V_ {rms} $$

$$ \ Rightarrow V_ {m} = 1.414 V_ {rms} $$

Nerede,

$ V_ {m} $, sinüzoidal (AC) giriş voltajı sinyalinin maksimum değeridir.

DC veya Tam dalga doğrultucunun çıkış sinyalinin ortalama değeri

$$ V_ {dc} = \ frac {2V_ {m}} {\ pi} $$

Substitute, yukarıdaki denklemdeki $ V_ {m} $ değeri

$$ V_ {dc} = \ frac {2 \ times 1,414 \: V_ {rms}} {\ pi} $$

$$ V_ {dc} = 0.9 \: V_ {rms} $$

Bu nedenle, AC voltmetre şuna eşit bir çıkış voltajı üretir. 0.9 sinüzoidal (AC) giriş voltajı sinyalinin rms değerinin katı.

Önceki bölümde, doğrultucu tabanlı AC voltmetreler hakkında tartıştık. Bu bölüm aşağıdaki iki tip AC voltmetreyi kapsar.

• Tepe yanıt veren AC voltmetre
• True RMS yanıt veren AC voltmetre

Şimdi, bu iki tip AC voltmetreyi tek tek tartışalım.

Tepe Yanıtlayan AC Voltmetre

Adından da anlaşılacağı gibi, en yüksek yanıt veren AC voltmetre yanıt verir peak valuesAC voltaj sinyali. Bu, bu voltmetrenin AC voltajlarının tepe değerlerini ölçtüğü anlamına gelir. circuit diagram tepe yanıt veren AC voltmetre aşağıda gösterilmiştir -

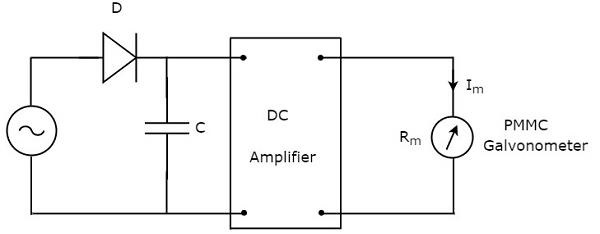
Yukarıdaki devre bir diyot, kapasitör, DC amplifikatör ve PMMC galvanometreden oluşur. Yukarıdaki devrede bulunan diyot, düzeltme amacıyla kullanılır. Böylece diyot, AC voltaj sinyalini DC voltaj sinyaline dönüştürür. Kapasitör, bu DC voltaj sinyalinin tepe değerine şarj olur.

Sırasında positive half cycleAC voltaj sinyali, diyot iletir ve kapasitör, AC voltaj sinyalinin tepe değerine şarj olur. AC voltaj sinyalinin değeri bu değerden düşük olduğunda, diyot ters taraflı olacaktır.

Böylece, kondansatör, AC voltaj sinyalinin bir sonraki pozitif yarı döngüsüne kadar DC amplifikatörün direnci yoluyla deşarj olacaktır. AC voltaj sinyalinin değeri kondansatör voltajından büyük olduğunda diyot iletir ve işlem tekrarlanır.

Bileşen değerlerini, kapasitör hızlı şarj olacak ve yavaş deşarj olacak şekilde seçmeliyiz. Sonuç olarak, sayaç her zaman bu kapasitör gerilimine yanıt verir, yanipeak value of AC voltage.

True RMS Yanıt Veren AC Voltmetre

Adından da anlaşılacağı gibi, gerçek RMS yanıt veren AC voltmetre, AC voltaj sinyalinin gerçek RMS değerlerine yanıt verir. Bu voltmetre, AC gerilimlerinin RMS değerlerini ölçer. circuit diagram Gerçek RMS yanıt veren AC voltmetre aşağıdaki şekilde gösterilmiştir.

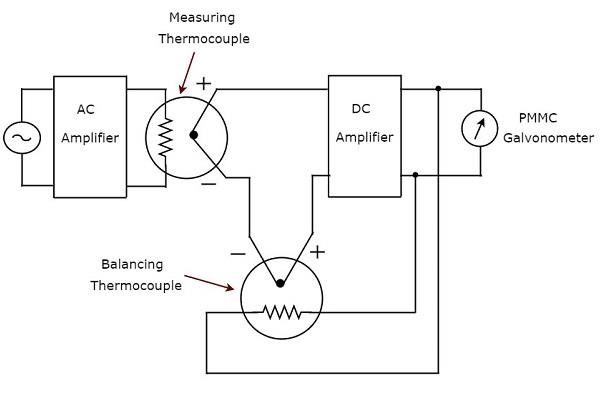
Yukarıdaki devre bir AC amplifikatör, iki termokupl, DC amplifikatör ve PMMC galvanometreden oluşur. AC amplifikatör, AC voltaj sinyalini güçlendirir. Yukarıdaki devrede kullanılan iki termokupl, bir ölçüm termokupl ve bir dengeleme termokupludur.Measuring thermocouple AC voltaj sinyalinin RMS değeri ile orantılı bir çıkış voltajı üretir.

Herhangi bir termokupl, girdi miktarının bir karesini normal bir miktara dönüştürür. Bu, bir termokuplun çıkışı ve girişi arasında doğrusal olmayan bir ilişki olduğu anlamına gelir. Bir termokuplun doğrusal olmayan davranışının etkisi, geri besleme devresinde başka bir termokupl kullanılarak ihmal edilebilir. Yukarıdaki devrede bu amaçla kullanılan termokupl,balancing thermocouple.

İki termokupl, yani termokupl ölçme ve dengeleme termokupl birlikte DC amplifikatörün girişinde bir gelin oluşturur. Sonuç olarak, ölçüm cihazı her zamantrue RMS value AC voltaj sinyali.

Akım, elektrik yükünün akış hızıdır. Bu elektrik yükü yalnızca bir yönde akarsa, ortaya çıkan akıma Doğru Akım (DC) denir. Aranan Doğru Akımı ölçmek için kullanılan aletDC ammeter.

Kalıcı Mıknatıslı Hareketli Bobin (PMMC) galvanometreye paralel bir direnç yerleştirirsek, tüm kombinasyon DC ampermetre görevi görür. DC ampermetrede kullanılan paralel direnç, şönt direnci olarak da adlandırılır veya basitçe,shunt. Büyük değerdeki DC akımını ölçmek için bu direncin değeri küçük kabul edilmelidir.

circuit diagram DC ampermetre aşağıdaki şekilde gösterilmiştir.

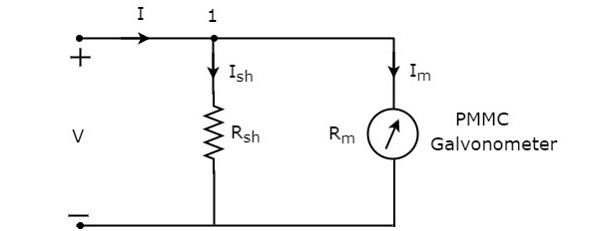
Bunu yerleştirmeliyiz DC ammeterDC akımının ölçülecek olduğu bir elektrik devresinin dalına seri olarak. Paralel bağlanan elemanlar arasındaki voltaj aynıdır. Dolayısıyla, şönt direnç üzerindeki voltaj, $ R_ {sh} $ ve galvanometre direnci üzerindeki voltaj $ R_ {m} $ aynıdır, çünkü bu iki eleman yukarıdaki devrede paralel olarak bağlanmıştır.Mathematicallyşu şekilde yazılabilir

$$ I_ {sh} R_ {sh} = I_ {m} R_ {m} $$

$ \ Rightarrow R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {sh}} $ (Denklem 1)

KCL equation 1. düğümde

$$ - I + I_ {sh} + I_ {m} = 0 $$

$$ \ Rightarrow I_ {sh} = I-I_ {m} $$

Substitute Denklem 1'deki $ I_ {sh} $ değeri.

$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I-I_ {m}} $ (Denklem 2)

Denklem 2'nin sağ tarafında bulunan payda teriminde ortak olarak $ I_ {m} $ alın

$$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {m} (\ frac {1} {I_ {m}} - 1)} $$

$ \ Rightarrow R_ {sh} = \ frac {R_ {m}} {\ frac {I} {I_ {m}} - 1} $ (Denklem 3)

Nerede,

$ R_ {sh} $ şönt direncidir

$ R_ {m} $ galvanometrenin iç direncidir

$ I $ ölçülecek toplam Doğru Akımdır

$ I_ {m} $ tam ölçekli sapma akımıdır

Ölçülecek toplam Doğru Akım oranı, $ I $ ve galvanometrenin tam ölçekli sapma akımı $ I_ {m} $ olarak bilinir multiplying factor, m. Matematiksel olarak şu şekilde temsil edilebilir:

$ m = \ frac {I} {I_ {m}} $ (Denklem 4)

$ R_ {sh} = \ frac {R_ {m}} {m-1} $ (Denklem 5)

Bulabiliriz value of shunt resistance Mevcut verilere göre Denklem 2 veya Denklem 5 kullanılarak.

Çok Aralıklı DC Ampermetre

Önceki bölümde, PMMC galvanometre ile paralel olarak bir direnç yerleştirilerek elde edilen DC ampermetreyi tartışmıştık. Bu DC ampermetre, ölçmek için kullanılabilir.particular range Doğrudan Akımlar.

Doğru Akımları ölçmek için DC ampermetre kullanmak istiyorsak multiple ranges, o zaman tek direnç yerine çoklu paralel dirençler kullanmalıyız ve bu direnç kombinasyonunun tamamı PMMC galvanometreye paraleldir. circuit diagram çok aralıklı DC ampermetre aşağıdaki şekilde gösterilmiştir.

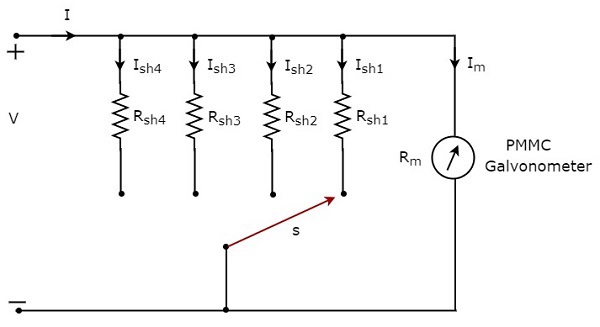
Bu çok aralıklı DC ampermetreyi, gerekli aralığın Doğru Akımının ölçüleceği bir elektrik devresinin dalına seri olarak yerleştirin. İstenen akım aralığı, anahtarları ilgili şönt direncine bağlayarak seçilir.

$ M_ {1}, m_ {2}, m_ {3} $ ve $ m_ {4} $ multiplying factorsToplam Direkt Akımların sırasıyla $ I_ {1}, I_ {2}, I_ {3} $ ve $ I_ {4} $ olarak ölçüldüğünü düşündüğümüzde DC ampermetrenin% 'si. Her çarpan faktöre karşılık gelen formüller aşağıdadır.

$$ m_ {1} = \ frac {I_ {1}} {I_ {m}} $$

$$ m_ {2} = \ frac {I_ {2}} {I_ {m}} $$

$$ m_ {3} = \ frac {I_ {3}} {I_ {m}} $$

$$ m_ {4} = \ frac {I_ {4}} {I_ {m}} $$

Yukarıdaki devrede, dört shunt resistors, $ R_ {sh1}, R_ {sh2}, R_ {sh2} $ ve $ R_ {sh4} $. Bu dört dirence karşılık gelen formüller aşağıdadır.

$$ R_ {sh1} = \ frac {R_ {m}} {m_ {1} -1} $$

$$ R_ {sh2} = \ frac {R_ {m}} {m_ {2} -1} $$

$$ R_ {sh3} = \ frac {R_ {m}} {m_ {3} -1} $$

$$ R_ {sh4} = \ frac {R_ {m}} {m_ {4} -1} $$

Yukarıdaki formüller, her bir şönt direncinin direnç değerlerini bulmamıza yardımcı olacaktır.

Akım, elektrik yükünün akış hızıdır. Bu elektrik yükünün yönü düzenli olarak değişirse, ortaya çıkan akım denir.Alternating Current (AC).

Elektrik devresinin herhangi bir dalından geçen Alternatif Akımı ölçmek için kullanılan cihaza denir. AC ammeter.

Example - Termokupl tipi AC ampermetre.

Şimdi, Termokupl tipi AC ampermetre hakkında konuşalım.

Termokupl Tipi AC Ampermetre

PMMC galvanometrenin önüne bir Termokupl bağlanırsa, bu kombinasyonun tamamına termokupl tipi AC ampermetre denir. block diagram Termokupl tipi AC ampermetre aşağıdaki şekilde gösterilmiştir.

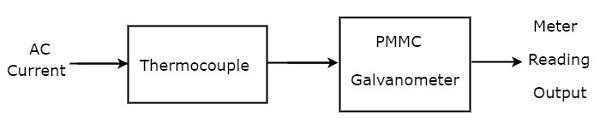
Yukarıdaki blok diyagram esas olarak iki bloktan oluşur: bir termokupl ve bir PMMC galvanometre. Sadece her bloğu yukarıdaki blok diyagramındaki ilgili bileşen (ler) ile değiştirerek ilgili devre şemasını alacağız. Böylececircuit diagram Termokupl tipi AC ampermetre aşağıdaki şekilde gösterildiği gibi görünecektir.

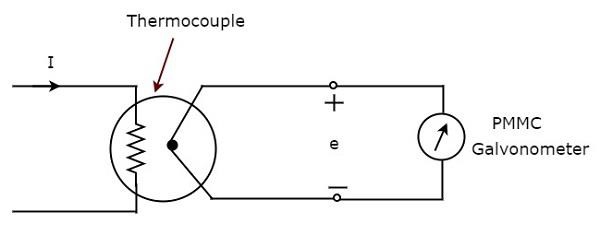
Termokupl, Alternatif Akım, ısıtıcı elemanından her aktığında bir EMF, $ e $ üretir. Bu EMF, $ e $, ısıtıcı elemanının içinden akan akımın rms değeri I ile doğru orantılıdır. Bu nedenle, okumak için PMMC cihazının ölçeğini kalibre etmeliyizrms values of current.

Bu nedenle, bu bölümle DC voltmetreler, AC voltmetreler, DC ampermetreler ve AC ampermetreler gibi tüm temel ölçüm aletlerini tamamladık. Bir sonraki bölümde, direnç değerini ölçen sayaçlar veya ölçüm cihazlarından bahsedelim.

Bir elektrik devresindeki herhangi iki nokta arasındaki direnç değerini ölçmek için kullanılan alete denir. ohmmeter. Bilinmeyen bir direncin değerini bulmak için de kullanılabilir. Direnç birimleri ohm ve ölçüm cihazı metredir. Böylece "ohmmetre" kelimesi kelimelerin birleştirilmesiyle elde edilir.“ohm” ve “meter”.

Ohmmetre Türleri

Aşağıdakiler two types Ohmmetreler.

• Ohmmetre Serisi
• Şönt Ohmmetre

Şimdi, bu iki tür ohmmetreyi tek tek tartışalım.

Ohmmetre Serisi

Direncin değeri bilinmiyorsa ve ohmmetre ile seri olarak yerleştirilerek ölçülmesi gerekiyorsa, bu ohmmetre seri ohmmetre olarak adlandırılır. circuit diagram Ohmmetre serisi aşağıdaki şekilde gösterilmiştir.

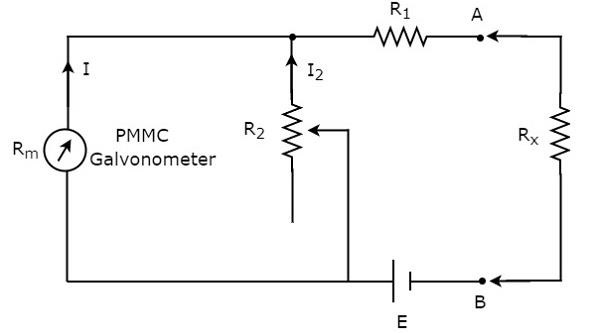
Devrenin A ve B terminallerinin sol tarafında kalan kısmı series ohmmeter. Böylece bilinmeyen direncin değerini A ve B terminallerinin sağ tarafına yerleştirerek ölçebiliriz.Şimdi,calibration scale Ohmmetre serisi.

• Eğer $ R_ {x} = 0 \: \ Omega $ ise, A ve B terminalleri birbirleriyle kısa devre yapacaktır. Böylece, sayaç akımı dirençler $ R_ {1} $ ve $ R_ {2} $ arasında bölünür. Şimdi, direncin değerini, $ R_ {2} $, tüm sayaç akımı dirençten geçecek şekilde değiştirin, sadece $ R_ {1} $. Bu durumda sayaç dolu gösterirscale deflection current. Dolayısıyla, sayacın bu tam ölçekli sapma akımı $ 0 \: \ Omega $ olarak temsil edilebilir.

• $ R_ {x} = \ infty \: \ Omega $ ise, A ve B terminalleri birbirleriyle açık devre olacaktır. Yani dirençten, $ R_ {1} $ hiçbir akım geçmez. Bu durumda, sayaç sıfır sapma akımını gösterir. Dolayısıyla, sayacın bu sıfır sapması $ \ infty \ Omega $ olarak temsil edilebilir.

• Bu şekilde, $ R_ {x} $ 'ın farklı değerlerini dikkate alarak, sayaç farklı sapmaları gösterir. Dolayısıyla, buna göre bu sapmaları karşılık gelen direnç değeri ile temsil edebiliriz.

Ohmmetre serisi bir kalibrasyon ölçeğinden oluşur. Ölçeğin sağ elinin ve sol elinin uç noktalarında sırasıyla 0 $ \ Omega $ ve $ \ infty \: \ Omega $ göstergeleri vardır. Seri ohmmetre ölçüm için kullanışlıdırhigh values of resistances.

Şönt Ohmmetre

Direncin değeri bilinmiyorsa ve ohmmetre ile paralel (şönt) yerleştirilerek ölçülecekse, bu ohmmetre şönt ohmmetre olarak adlandırılır. circuit diagram şönt ohmmetre aşağıdaki şekilde gösterilmiştir.

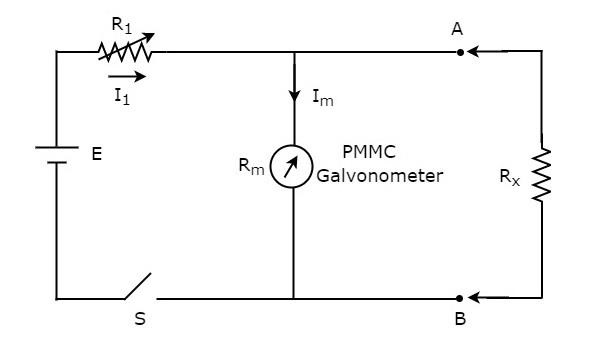
Devrenin A ve B terminallerinin sol tarafında kalan kısmı shunt ohmmeter. Böylece bilinmeyen direncin değerini A ve B terminallerinin sağ tarafına yerleştirerek ölçebiliriz.

Şimdi, konuşalım calibration scaleşönt ohmmetre. Kullanımdayken yukarıdaki devrenin S anahtarını kapatın.

• Eğer $ R_ {x} = 0 \: \ Omega $ ise, A ve B terminalleri birbirleriyle kısa devre yapacaktır. Bundan dolayı, tüm akım $ I_ {1} $ A ve B terminallerinden geçer. Bu durumda PMMC galvanometreden akım geçmez. Bu nedenle,null deflection PMMC galvanometrenin% 0 \: \ Omega $ olarak temsil edilebilir.

• $ R_ {x} = \ infty \: \ Omega $ ise, A ve B terminalleri birbirleriyle açık devre olacaktır. Dolayısıyla, A ve B terminallerinden akım geçmez. Bu durumda, akımın tamamı, $ I_ {1} $ PMMC galvanometreden geçer. Gerekirse, PMMC galvanometre tam ölçekli sapma akımını gösterene kadar direncin değerini $ R_ {1} $ değiştirin (ayarlayın). Dolayısıyla bufull scale deflection PMMC galvanometrenin akımı $ \ infty \: \ Omega $ olarak temsil edilebilir

• Bu şekilde, $ R_ {x} $ 'ın farklı değerlerini dikkate alarak, sayaç farklı sapmaları gösterir. Dolayısıyla, buna göre bu sapmaları karşılık gelen direnç değerleri ile temsil edebiliriz.

Şönt ohmmetre bir kalibrasyon ölçeğinden oluşur. Ölçeğin sol elinin ve sağ elinin uç noktalarında sırasıyla $ 0 \: \ Omega $ ve $ \ infty \: \ Omega $ göstergeleri vardır.

Şönt ohmmetre ölçüm için kullanışlıdır low values of resistances. Bu nedenle, ölçülecek direnç değerlerine, yani yüksek veya düşük değerlerine dayalı olarak seri ohmmetre veya şönt ohmmetre kullanabiliriz.

Önceki bölümlerde voltmetreler, ampermetreler ve ohmmetreler hakkında tartışmıştık. Bu ölçüm cihazları sırasıyla voltaj, akım ve direnci ölçmek için kullanılır. Bunun anlamı bizdeseparate measuring instruments voltaj, akım ve direnci ölçmek için.

Diyelim ki, gerilim, akım ve direnç gibi miktarları tek tek ölçmek için tek bir ölçüm cihazı kullanılabiliyorsa, o zaman multimeter. Aynı anda birden fazla elektriksel miktarı ölçebildiği için multimetre adını almıştır.

Multimetre kullanarak ölçümler

MultimeterDC ve AC voltajlarını, DC ve AC akımlarını ve çeşitli aralıklardaki dirençleri ölçmek için kullanılan bir araçtır. Elektronik Multimetre veya Gerilim Ohm Ölçer (VOM) olarak da adlandırılır.

DC voltaj Ölçümü

Parçası circuit diagram DC voltajını ölçmek için kullanılabilen Multimetre aşağıdaki şekilde gösterilmiştir.

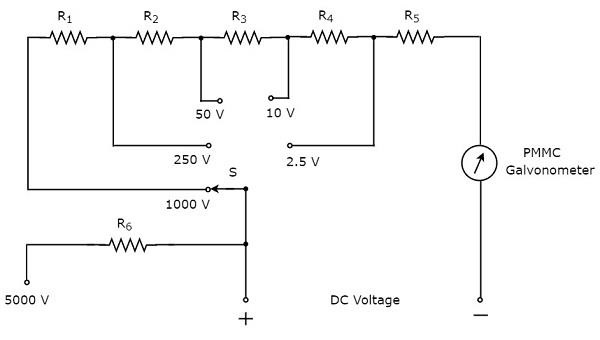
Yukarıdaki devre, çok menzilli bir DC voltmetreye benziyor. PMMC galvanometre ile seri olarak bir direncin kombinasyonu,DC voltmeter. Böylece belirli bir değere kadar DC voltajlarını ölçmek için kullanılabilir.

Aynı DC voltmetre ile ölçülebilen DC gerilim aralığını direnç değerini artırarak artırabiliriz. dirençleri bağladığımızda eşdeğer direnç değeri artarseries.

Yukarıdaki devrede, DC voltajlarını en fazla ölçebiliriz. 2.5VDirenç kombinasyonunu kullanarak, seri olarak PMMC galvanometre ile $ R_ {5} $. Bir önceki devre ile seri olarak $ R_ {4} $ direnç bağlayarak, en fazla DC gerilimleri ölçebiliriz.10V. Bu şekilde, önceki (önceki) devreye seri olarak bir direnç bağlayarak DC voltaj aralığını artırabiliriz.

S anahtarını istenen voltaj aralığına bağlayarak bir elektrik devresinin herhangi iki noktasındaki DC voltajını ölçebiliriz.

DC Akım Ölçümü

Parçası circuit diagram DC akımını ölçmek için kullanılabilen Multimetre aşağıdaki şekilde gösterilmiştir.

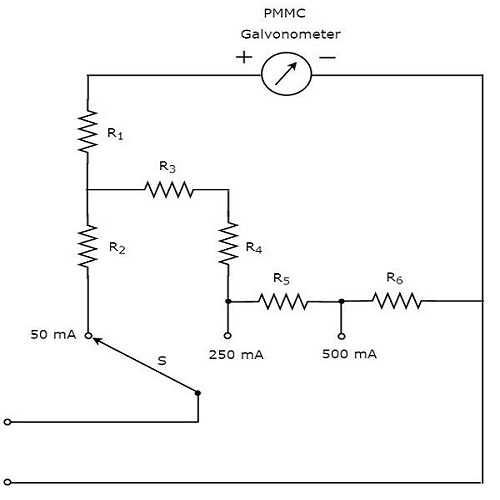
Yukarıdaki devre, çok menzilli bir DC ampermetreye benziyor. PMMC galvanometre ile paralel bir direncin kombinasyonu birDC ammeter. Böylece belirli bir değere kadar DC akımlarını ölçmek için kullanılabilir.

Alabiliriz different rangesDirençleri önceki dirençle paralel yerleştirerek aynı DC ampermetre ile ölçülen DC akımlarının oranı. Yukarıdaki devrede, yüksek akım nedeniyle sayacın hasar görmesini önlemek için direnç, $ R_ {1} $ PMMC galvanometre ile seri olarak bağlanır.

S anahtarını istenen akım aralığına bağlayarak bir elektrik devresinin herhangi iki noktasından geçen DC akımını ölçebiliriz.

AC voltaj ölçümü

Parçası circuit diagram AC voltajını ölçmek için kullanılabilen Multimetre aşağıdaki şekilde gösterilmiştir.

Yukarıdaki devre bir multi range AC voltmeter. DC voltmetre ile seri (kaskad) doğrultucu yerleştirerek AC voltmetre elde edeceğimizi biliyoruz. Yukarıdaki devre sadece diyot kombinasyonu ve direnci, direnç, $ R_ {5} $ ve PMMC galvanometre arasına $ R_ {6} $ yerleştirilerek oluşturulmuştur.

S anahtarını istenen voltaj aralığına bağlayarak bir elektrik devresinin herhangi iki noktasındaki AC voltajını ölçebiliriz.

Direnç Ölçümü

Parçası circuit diagram Direnci ölçmek için kullanılabilecek Multimetre aşağıdaki şekilde gösterilmiştir.

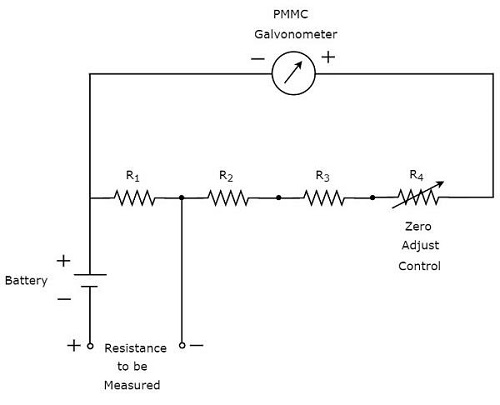
Herhangi bir ölçüm yapmadan önce aşağıdaki iki görevi yapmalıyız.

• Cihazı kısa devre yapın
• Sayaç tam ölçekli akımı gösterene kadar sıfır ayar kontrolünü değiştirin. Yani sayaç sıfır direnç değerini gösterir.

Şimdi, yukarıdaki devre şönt ohmmetre gibi davranır ve ölçek çarpımı 1'dir, yani 10 ⁰ . Yüksek dirençleri ölçmek için ölçek çarpımları olarak 10'un daha yüksek dereceli güçlerini de düşünebiliriz.

Signal generator sinüs dalgası, kare dalga, üçgen dalga vb. standart test sinyallerini sağlayan elektronik bir ekipmandır. Periyodik sinyaller ürettiği için osilatör olarak da adlandırılır.

Bir Ses Frekansı (AF) aralığına sahip periyodik sinyali üreten sinyal oluşturucu, AF signal generator. ses frekanslarının aralığı 20Hz ila 20KHz'dir.

AF Sinüs ve Kare Dalga Üreteci

Gereksinime göre ses frekansları aralığında sinüs dalgası veya kare dalga üreten AF sinyal oluşturucu, AF Sinüs ve Kare dalga üreteci olarak adlandırılır. Onunblock diagramaşağıdaki şekilde gösterilmiştir.

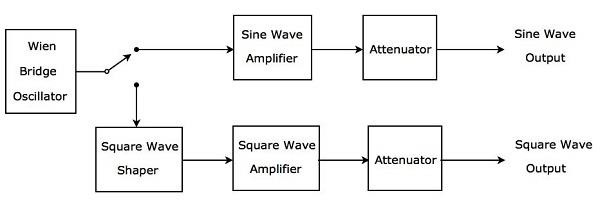
Yukarıdaki blok diyagram esas olarak şunlardan oluşur: two paths. Bunlar üst yol ve alt yoldur. Üst yol, AF sinüs dalgası oluşturmak için kullanılır ve alt yol, AF kare dalgası oluşturmak için kullanılır.

Wien bridge oscillatorses frekansları aralığında bir sinüs dalgası üretecektir. İhtiyaca bağlı olarak, Wien köprü osilatörünün çıkışını bir anahtarla üst yola veya alt yola bağlayabiliriz.

Üst yol, sinüs dalgası yükseltici ve zayıflatıcı gibi bloklardan oluşur. Anahtar, Wien köprü osilatörünün çıkışını üst yola bağlamak için kullanılırsa, istenen birAF sine wave üst yolun çıkışında.

Alt yol şu bloklardan oluşur: kare dalga şekillendirici, kare dalga yükseltici ve zayıflatıcı. Kare dalga şekillendirici, sinüs dalgasını kare dalgaya dönüştürür. Anahtar, Wien köprü osilatörünün çıkışını daha düşük yola bağlamak için kullanılırsa, istenen birAF square wavealt yolun çıkışında. Bu şekilde, düşündüğümüz blok diyagram, ihtiyaca göre AF sinüs dalgası veya AF kare dalgası üretmek için kullanılabilir.

Fonksiyon üreticisi

Fonksiyon üreteci, üç veya daha fazla periyodik dalga üreten bir sinyal oluşturucudur. Aşağıdakileri göz önünde bulundurblock diagram Üçgen dalga, kare dalga ve sinüs dalgası gibi periyodik dalgalar üretecek bir Fonksiyon üreteci.

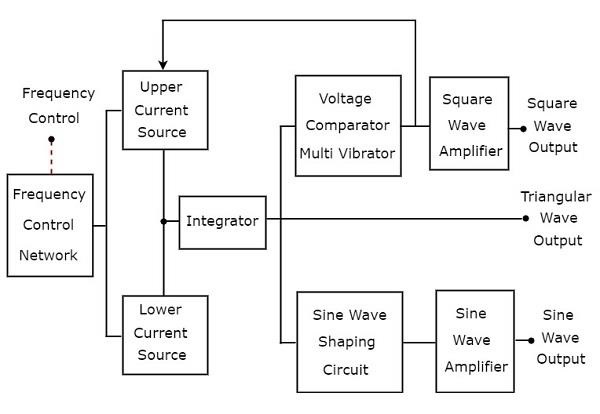
İki tane current sources, yani yukarıdaki blok diyagramında üst akım kaynağı ve alt akım kaynağı. Bu iki akım kaynağı, frekans kontrollü voltaj tarafından düzenlenir.

Üçgen Dalga

IntegratorYukarıdaki blok diyagramında bulunan, üst ve alt akım kaynaklarından dönüşümlü olarak eşit süre için tekrar tekrar sabit akım alır. Dolayısıyla, entegratör aynı anda art arda iki tür çıktı üretecektir -

• Bir entegratörün çıkış voltajı increases linearly Entegratörün üst akım kaynağından akım aldığı süreye göre.

• Bir entegratörün çıkış voltajı decreases linearly Entegratörün düşük akım kaynağından akım aldığı süre için zamana göre.

Bu şekilde, yukarıdaki blok diyagramda bulunan entegratör bir triangular wave.

Kare Dalga ve Sinüs Dalgası

Entegratör çıkışı, yani üçgen dalga, sırasıyla kare dalga ve sinüs dalgasını elde etmek için yukarıdaki blok diyagramda gösterildiği gibi diğer iki bloğa bir girdi olarak uygulanır. Gelin bu ikisini tek tek tartışalım.

Kare dalgası

Üçgen dalganın pozitif eğimi ve negatif eğimi dönüşümlü olarak eşit süre için tekrar tekrar vardır. Böylecevoltage comparator multi vibrator Yukarıdaki blok diyagramında bulunanlar, aşağıdaki iki tip çıktıyı eşit süre için tekrar tekrar üretecektir.

• Bir tür sabit (higher) voltage gerilim karşılaştırıcı çoklu vibratör çıkışında, gerilim karşılaştırıcı çoklu vibratörün üçgen dalganın pozitif eğimini aldığı süre için.

• Başka bir tür sabit (lower) voltage gerilim karşılaştırıcı çoklu vibratör çıkışında, gerilim karşılaştırıcı çoklu vibratörün üçgen dalganın negatif eğimini aldığı süre için.

Yukarıdaki blok diyagramda bulunan voltaj karşılaştırıcı çoklu vibratör bir square wave. Gerilim karşılaştırıcı multi vibratör çıkışında üretilen kare dalganın genliği yeterli değilse kare dalga amplifikatör kullanılarak istenilen değere yükseltilebilir.

Sinüs dalgası

sine wave shaping circuitüçgen giriş dalgasından bir sinüs dalgası çıkışı üretecektir. Temel olarak, bu devre bir diyot direnç ağından oluşur. Sinüs dalgası şekillendirme devresi çıkışında üretilen sinüs dalgasının genliği yetersiz ise sinüs dalgası amplifikatörü kullanılarak istenilen değere yükseltilebilir.

Dalgaları analiz etmek için kullanılan elektronik alete denir wave analyzer. Sinyal ve dalga terimleri sık sık birbirinin yerine kullanılabildiğinden sinyal analizörü olarak da adlandırılır.

Temsil edebiliriz periodic signal aşağıdaki iki terimin toplamı olarak.

• DC bileşeni
• Bir dizi sinüzoidal harmonik

Yani, periyodik bir sinyalin analizi, içinde bulunan harmonik bileşenlerinin analizidir.

Temel Dalga Analizörü

Temel dalga analizörü temel olarak üç bloktan oluşur - birincil dedektör, tam dalga doğrultucu ve PMMC galvanometre. block diagram temel dalga analizörü aşağıdaki şekilde gösterilmiştir -

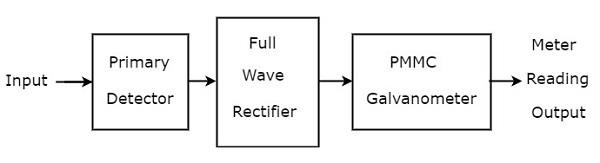
function Temel dalga analizöründe bulunan her bloğun sayısı aşağıda belirtilmiştir.

• Primary Detector- Bir LC devresinden oluşur. İndüktör, L ve kapasitör C değerlerini, sadece ölçülecek istenen harmonik frekans bileşenine izin verecek şekilde ayarlayabiliriz.

• Full Wave Rectifier - AC girişini DC çıkışına dönüştürür.

• PMMC Galvanometer - Tam dalga doğrultucu çıkışında elde edilen sinyalin tepe değerini gösterir.

Temel dalga analizörünün yukarıdaki blok diyagramında her bloğu ilgili bileşen (ler) ile değiştirerek ilgili devre şemasını alacağız. Böylececircuit diagram Temel dalga analizörü aşağıdaki şekilde gösterildiği gibi görünecektir -

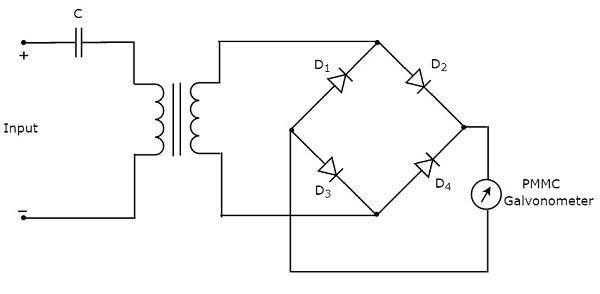
Bu temel dalga analizörü, periyodik bir sinyalin her bir harmonik frekans bileşenini analiz etmek için kullanılabilir.

Dalga Analizörü Türleri

Dalga analizörleri aşağıdaki şekilde sınıflandırılabilir two types.

• Frekans Seçici Dalga Analizörü
• Süperheterodin Dalga Analizörü

Şimdi bu iki dalga analizörünü tek tek tartışalım.

Frekans Seçici Dalga Analizörü

Sinyalleri analiz etmek için kullanılan dalga analizörü, AF aralığına sahiptir ve frekans seçici dalga analizörü olarak adlandırılır. block diagram frekans seçici dalga analizörü aşağıdaki şekilde gösterilmiştir.

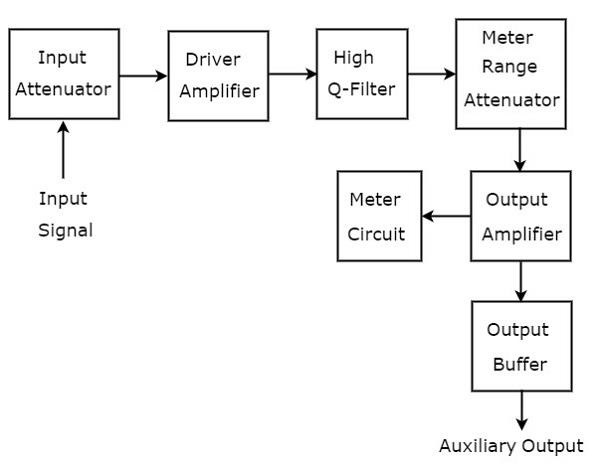
Frekans seçici dalga analizörü bir dizi bloktan oluşur. function her bloğun sayısı aşağıda belirtilmiştir.

• Input Attenuator- Analiz edilecek AF sinyali, giriş zayıflatıcıya uygulanır. Sinyal genliği çok büyükse, giriş zayıflatıcısı ile zayıflatılabilir.

• Driver Amplifier - Gerektiğinde alınan sinyali güçlendirir.

• High Q-filter- İstenilen frekansı seçmek ve istenmeyen frekansları reddetmek için kullanılır. İki RC bölümü ve iki filtre amplifikatöründen oluşur ve bunların tümü birbiriyle kademeli olarak bağlanır. 10'un katlarında frekans aralığını değiştirmek için kapasitans değerlerini değiştirebiliriz. Benzer şekilde, frekansı seçilen bir aralıkta değiştirmek için direnç değerlerini değiştirebiliriz.

• Meter Range Attenuator - Seçilen AF sinyalini giriş olarak alır ve gerektiğinde zayıflatılmış bir çıkış üretir.

• Output Amplifier - Gerekirse seçilen AF sinyalini güçlendirir.

• Output Buffer - Seçilen AF sinyalini çıkış cihazlarına sağlamak için kullanılır.

• Meter Circuit- Seçilen AF sinyalinin okumasını görüntüler. Volt aralığında veya desibel aralığında sayaç okumasını seçebiliriz.

Süperheterodin Dalga Analizörü

RF aralığının sinyallerini analiz etmek için kullanılan dalga analizörü, süperheterodin dalga analizörü olarak adlandırılır. Aşağıdaki şekil,block diagram süperheterodin dalga analizörü.

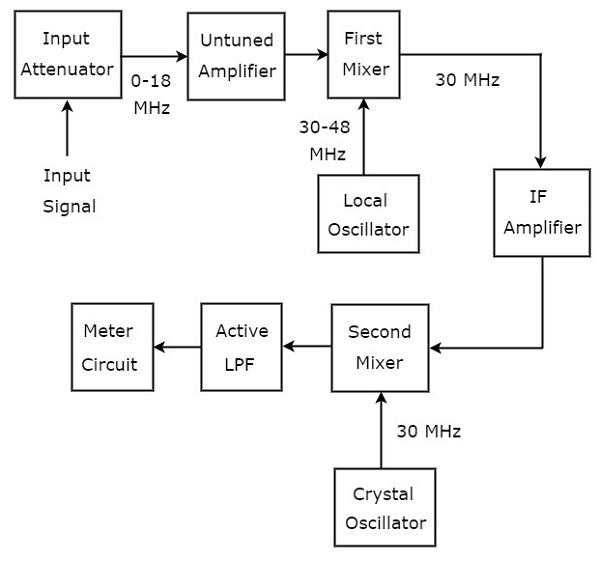
working süperheterodin dalga analizörü aşağıda belirtilmiştir.

• Analiz edilecek olan RF sinyali giriş zayıflatıcıya uygulanır. Sinyal genliği çok büyükse, bu durumda zayıflatılabilir.input attenuator.

• Untuned amplifier Gerektiğinde RF sinyalini yükseltir ve ilk miksere uygulanır.

• Yerel osilatörün RF sinyali ve çıkışının frekans aralıkları sırasıyla 0-18 MHz ve 30-48 MHz'dir. Yani,first mixer30 MHz frekansa sahip bir çıktı üretir. Bu, kendisine uygulanan iki sinyalin frekanslarının farkıdır.

• IF amplifierAra Frekans (IF) sinyalini, yani birinci mikserin çıkışını yükseltir. Güçlendirilmiş IF sinyali ikinci miksere uygulanır.

• Kristal osilatörün yükseltilmiş IF sinyalinin ve çıkışının frekansları aynıdır ve 30MHz'e eşittir. Böylecesecond mixer0 Hz frekansa sahip bir çıktı üretir. Bu, kendisine uygulanan iki sinyalin frekanslarının farkıdır.

• Kesme frekansı Active Low Pass Filter (LPF)1500 Hz olarak seçilmiştir. Dolayısıyla bu filtre, ikinci karıştırıcının çıkış sinyaline izin verir.

• Meter CircuitRF sinyalinin okumasını gösterir. Volt aralığında veya desibel aralığında sayaç okumasını seçebiliriz.

Böylece, analiz edilecek sinyalin frekans aralığına bağlı olarak belirli bir dalga analizörü seçebiliriz.

Frekans alanındaki dalgaları analiz etmek için kullanılan elektronik alet denir spectrum analyzer. Temel olarak, CRT ekranında bir sinyalin enerji dağılımını gösterir. Burada, x ekseni frekansı ve y ekseni genliği temsil eder.

Spektrum Analizörü Türleri

Spektrum analizörlerini aşağıdaki şekilde sınıflandırabiliriz two types.

• Filtre Bankası Spektrum Analizörü
• Süperheterodin Spektrum Analizörü

Şimdi bu iki spektrum analizörünü tek tek tartışalım.

Filtre Bankası Spektrum Analizörü

Sinyalleri analiz etmek için kullanılan spektrum analizörü, AF aralığına filtre bankası spektrum analizörü denir veya real time spectrum analyzer çünkü tüm giriş frekanslarındaki herhangi bir değişikliği gösterir (görüntüler).

Aşağıdaki şekil, block diagram filtre bankası spektrum analizörü.

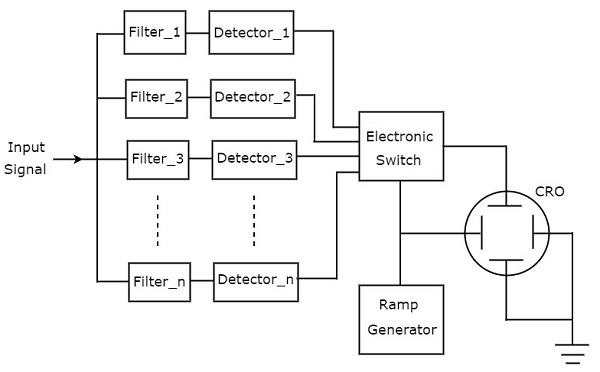
working filtre bankası spektrum analizörü aşağıda belirtilmiştir.

• Bir dizi bant geçiş filtresine sahiptir ve her biri belirli bir frekans bandına izin verecek şekilde tasarlanmıştır. Her bir bant geçiş filtresinin çıkışı, karşılık gelen bir detektöre verilir.

• Tüm dedektör çıkışları Elektronik anahtara bağlıdır. Bu anahtar, dedektör çıkışlarının CRO'nun dikey saptırma plakasına sıralı olarak verilmesini sağlar. Böylece, CRO frekansı görüntülerspectrum of AF signal CRT ekranında.

Süperheterodin Spektrum Analizörü

Sinyalleri analiz etmek için kullanılan spektrum analizörüne RF aralığı denir. superheterodyne spectrum analyzer. Onunblock diagram aşağıdaki şekilde gösterilmiştir.

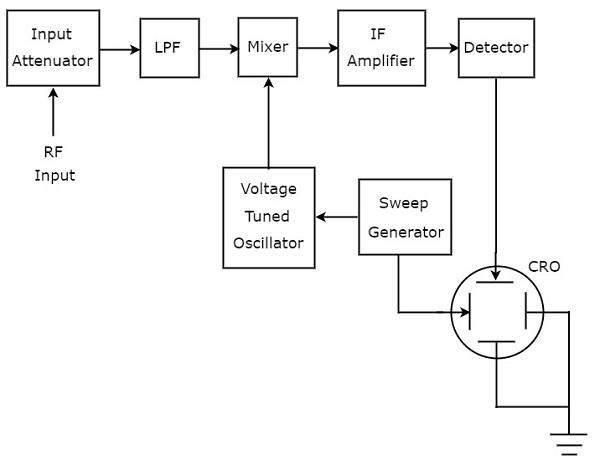
working süperheterodin spektrum analizörü aşağıda belirtilmiştir.

• Analiz edilecek RF sinyali giriş zayıflatıcıya uygulanır. Sinyal genliği çok büyükse, bir sinyal genliği ile zayıflatılabilir.input attenuator.

• Low Pass Filter (LPF) yalnızca kesme frekansından daha düşük olan frekans bileşenlerine izin verir.

• MixerAlçak geçiren filtre ve voltaj ayarlı osilatörden girişleri alır. Kendisine uygulanan iki sinyalin frekans farkı olan bir çıktı üretir.

• IF amplifierAra Frekans (IF) sinyalini, yani mikser çıkışını yükseltir. Güçlendirilmiş IF sinyali detektöre uygulanır.

Dedektörün çıkışı, CRO'nun dikey saptırma plakasına verilir. Böylece, CRO frekansı görüntülerspectrum of RF signal CRT ekranında.

Böylece, analiz edilecek sinyalin frekans aralığına bağlı olarak belirli bir spektrum analizörü seçebiliriz.

Oscilloscopebir voltaj dalga biçimini gösteren elektronik bir ekipmandır. Osiloskoplar arasında Katot Işınlı Osiloskop (CRO) temel olanıdır ve zamanla değişen bir sinyal veya dalga formu gösterir.

Bu bölümde, CRO'nun blok diyagramını ve bazı parametrelerin CRO kullanarak ölçümlerini tartışalım.

CRO'nun Blok Şeması

Katot Işınlı Osiloskop (CRO) bir dizi bloktan oluşur. Bunlar dikey amplifikatör, gecikme hattı, tetik devresi, zaman bazlı jeneratör, yatay amplifikatör, Katot Işın Tüpü (CRT) ve güç kaynağıdır. block diagram CRO oranı aşağıdaki şekilde gösterilmiştir.

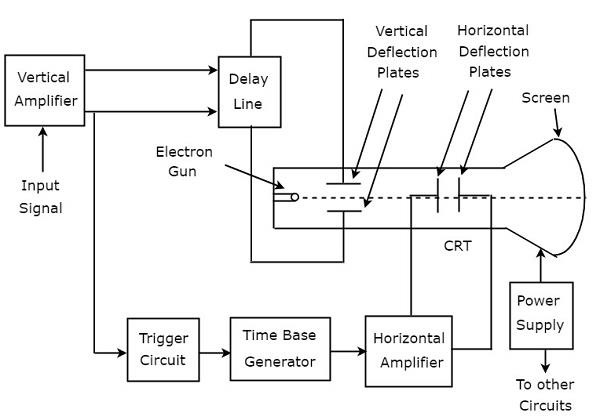
function CRO'nun her bloğunun sayısı aşağıda belirtilmiştir.

• Vertical Amplifier - CRT ekranında görüntülenecek giriş sinyalini güçlendirir.

• Delay Line- Dikey amplifikatörün çıkışında elde edilen sinyale bir miktar gecikme sağlar. Bu gecikmiş sinyal daha sonra CRT'nin dikey saptırma plakalarına uygulanır.

• Trigger Circuit - Elektron ışınının hem yatay hem de dikey sapmalarını senkronize etmek için bir tetikleme sinyali üretir.

• Time base Generator - Elektron ışınının yatay sapması için yararlı olan testere dişi sinyali üretir.

• Horizontal Amplifier - Testere dişi sinyalini güçlendirir ve ardından CRT'nin yatay saptırma plakalarına bağlar.

• Power supply- Hem yüksek hem de düşük voltaj üretir. Negatif yüksek voltaj ve pozitif düşük voltaj sırasıyla CRT ve diğer devrelere uygulanır.

• Cathode Ray Tube (CRT)- CRO'nun en önemli bloğudur ve esas olarak dört bölümden oluşur. Bunlar elektron tabancası, dikey saptırma plakaları, yatay saptırma plakaları ve floresan ekrandır.

Bir elektron tabancası tarafından üretilen elektron ışını, sırasıyla bir çift dikey saptırma plakası ve bir çift yatay saptırma plakası tarafından hem dikey hem de yatay yönde saptırılır. Son olarak, yön değiştiren ışın, flüoresan ekranda bir nokta olarak görünecektir.

Bu şekilde, CRO, CRT ekranında uygulanan giriş sinyalini gösterecektir. Böylece CRO kullanarak sinyalleri zaman alanında analiz edebiliriz.

CRO kullanarak ölçümler

CRO kullanarak aşağıdaki ölçümleri yapabiliriz.

• Genlik Ölçümü
• Zaman Dönemi Ölçümü
• Frekans Ölçümü

Şimdi bu ölçümleri tek tek tartışalım.

Genlik Ölçümü

CRO, voltaj sinyalini ekranında zamanın bir işlevi olarak görüntüler. amplitude bu voltaj sinyalinin değeri sabittir, ancak voltaj sinyalini dikey yönde kapsayan bölümlerin sayısını değiştirerek değiştirebiliriz. volt/divisionCRO panelindeki düğme. Bu nedenle, alacağızamplitude Aşağıdaki formül kullanılarak CRO ekranında bulunan sinyalin

$$ A = j \ kere n_ {v} $$

Nerede,

$ A $ genliktir

$ j $ volt / bölme değeridir

$ n_ {v} $, sinyali dikey yönde kapsayan bölümlerin sayısıdır.

Zaman Dönemi Ölçümü

CRO, voltaj sinyalini ekranında zamanın bir işlevi olarak görüntüler. Time period Bu periyodik voltaj sinyalinin değeri sabittir, ancak yatay yönde bir tam voltaj sinyali döngüsünü kapsayan bölümlerin sayısını değiştirerek değiştirebiliriz. time/division CRO panelindeki düğme.

Bu nedenle, alacağız Time period Aşağıdaki formül kullanılarak CRO ekranında bulunan sinyalin

$$ T = k \ kere n_ {h} $$

Nerede,

$ T $, Zaman dönemidir

$ j $, zamanın / bölümün değeridir

$ n_ {v} $, periyodik sinyalin yatay yönde bir tam döngüsünü kapsayan bölümlerin sayısıdır.

Frekans Ölçümü

Periyodik bir sinyalin frekansı f, zaman periyodunun T tersidir. Mathematicallyşu şekilde temsil edilebilir:

$$ f = \ frac {1} {T} $$

Böylece, bu iki adımı izleyerek periyodik bir sinyalin frekansını, f bulabiliriz.

• Step1 - Bul Time period periyodik sinyalin

• Step2 - Al reciprocal Adım 1'de elde edilen periyodik sinyalin Zaman periyodu

Bir sonraki bölümde özel amaçlı osiloskopları tartışacağız.

Önceki bölümde, temel bir osiloskop olan Katot Işınlı Osiloskop (CRO) hakkında tartışmıştık. Sadece ihtiyaca göre temel osiloskopa birkaç ek blok ekleyerek özel amaçlı osiloskoplar elde edeceğiz.

Aşağıdakiler special purpose oscilloscopes.

• Çift Kirişli Osiloskop
• Çift İzli Osiloskop
• Dijital Depolama Osiloskopu

Şimdi bu özel amaçlı osiloskopları tek tek tartışalım.

Çift Kirişli Osiloskop

İki voltaj dalga formu gösteren Osiloskop, Çift Işın Osiloskopu olarak adlandırılır. Onunblock diagram aşağıdaki şekilde gösterilmiştir.

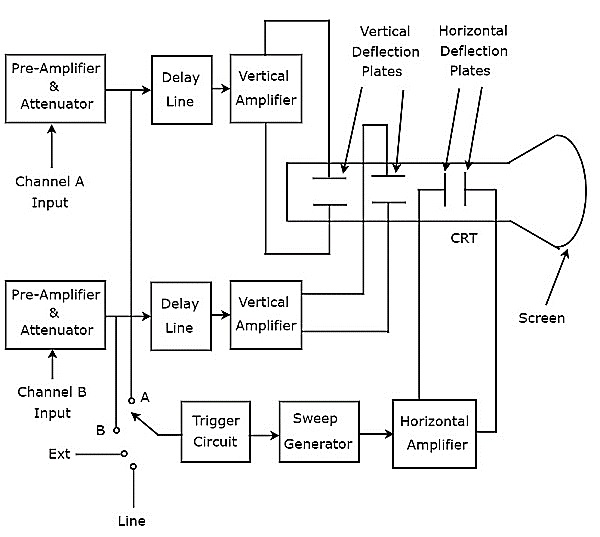
Yukarıdaki şekilde gösterildiği gibi, Çift Huzmeli Osiloskobun CRT'si iki set dikey saptırma plakasından ve bir set yatay saptırma plakasından oluşur.

Aşağıdaki blokların birleşimine a channel.

• Ön Amplifikatör ve Zayıflatıcı
• Gecikme Hattı
• Dikey Amplifikatör
• Bir dizi Dikey Saptırma Plakası

Çift Işın Osiloskopunda iki kanal vardır. Böylece, sırasıyla A ve B kanallarının girişi olarak A ve B olmak üzere iki sinyali uygulayabiliriz. Bu dört sinyalden herhangi birini şu şekilde seçebiliriz:trigger inputbir anahtar kullanarak tetik devresine. Bunlar giriş sinyalleri A ve B, Harici sinyal (Ext) ve Hat girişidir.

Bu osiloskop, iki çift dikey saptırma plakası bulunduğundan, dikey olarak döndürülmüş iki ışın üretecektir. Bu osiloskopta, ışını yatay yönde saptırmak için yararlı olan bloklar, her iki giriş sinyali için ortaktır. Son olarak, bu osiloskop,two input signals CRT ekranında aynı anda.

Çift İzli Osiloskop

Ekranda iki iz oluşturan Osiloskopa Çift İzli Osiloskop denir. Onunblock diagram aşağıdaki şekilde gösterilmiştir.

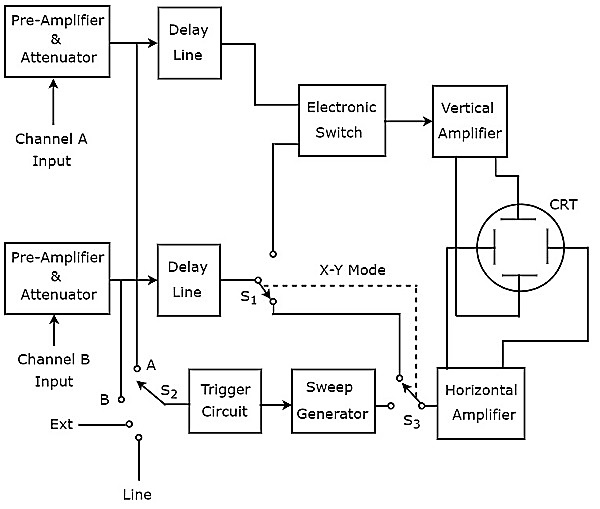
Yukarıdaki şekilde gösterildiği gibi, Çift İzli Osiloskobun CRT'si bir dizi dikey saptırma plakasından ve başka bir yatay saptırma plakasından oluşur. kanal dört bloktan oluşur, yani ön Amplifikatör ve zayıflatıcı, gecikme hattı, dikey amplifikatör ve dikey saptırma plakaları.

Yukarıdaki blok diyagramda, ilk iki blok her iki kanalda ayrı ayrı mevcuttur. Son iki blok, her iki kanal için ortaktır. Bu nedenle, yardımıylaelectronic switch belirli bir kanalın gecikme hattı çıkışını dikey amplifikatöre bağlayabiliriz.

Bu dört sinyalden herhangi birini tetikleyici giriş olarak seçebiliriz. trigger circuitbir anahtar kullanarak. Bunlar giriş sinyalleri A ve B, Harici sinyal (Ext) ve Hat girişidir.

Bu osiloskop, bir elektronik anahtar kullanarak A ve B giriş sinyallerini dikey yönde saptırmak için aynı elektron ışını kullanır ve two traces. ışını yatay olarak saptıran bloklar, her iki giriş sinyali için ortaktır.

Dijital Depolama Osiloskopu

Dalga biçimini dijital olarak depolayan osiloskop, dijital depolamalı osiloskop olarak bilinir. block diagram (dijital) depolama osiloskopu aşağıda -

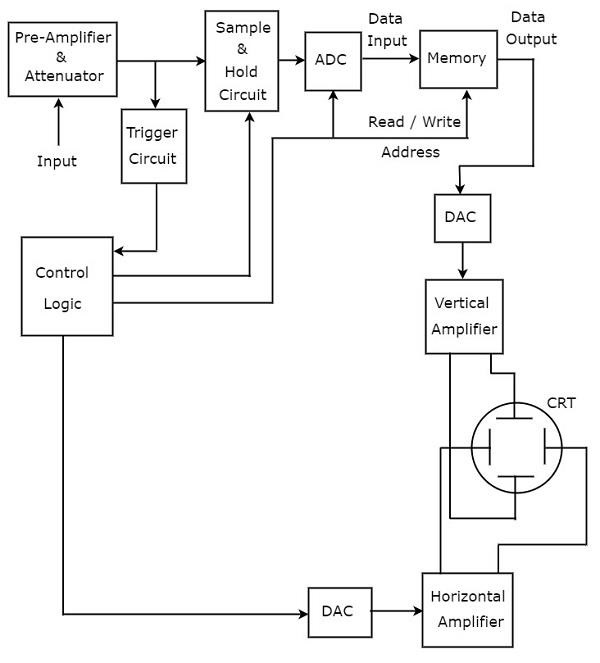
Dijital veri depolama için gerekli ek bloklar, onu bir Dijital Depolama Osiloskobuna dönüştürmek için temel bir osiloskopa eklenir. İçin gerekli bloklarstoring of digital dataDijital Depolama Osiloskopunda ön amplifikatör ve zayıflatıcı ile dikey amplifikatör arasında yer alır. Bunlar Örnekleme ve Tutma devresi, Analogdan Dijitale Dönüştürücü (ADC), Bellek ve Dijitalden Analog'a Dönüştürücüdür.

Control logicçeşitli kontrol sinyalleri göndererek ilk üç bloğu kontrol eder. Kontrol mantığı ve Dijital-Analog Dönüştürücü gibi bloklar, Dijital Depolama Osiloskopunda tetikleme devresi ile yatay amplifikatör arasında bulunur.

Dijital Depolama Osiloskopu stores the datadalga formunu ekranda görüntülemeden önce dijital olarak. Oysa temel osiloskop bu özelliğe sahip değildir.

Lissajous figureCRO'nun hem yatay hem de dikey saptırma plakalarına sinüzoidal sinyaller uygulandığında ekranda görüntülenen modeldir. Bu modeller, CRO'nun hem yatay hem de dikey saptırma plakalarına uygulanan sinüzoidal sinyallerin genliklerine, frekanslarına ve faz farklılıklarına bağlı olarak değişecektir.

Aşağıdaki şekil bir example Lissajous figürü.

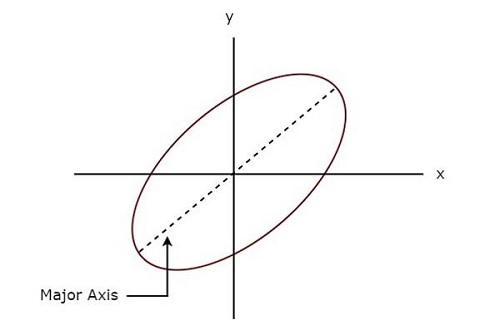
Yukarıdaki Lissajous figürü elliptical shape ve ana ekseni, pozitif x ekseni ile bir miktar eğim açısına sahiptir.

Lissajous Figürleri kullanarak ölçümler

Aşağıdakileri yapabiliriz two measurements bir Lissajous figüründen.

• Sinüzoidal sinyalin frekansı
• İki sinüzoidal sinyal arasındaki faz farkı

Şimdi bu iki ölçümü tek tek tartışalım.

Frekans Ölçümü

Sinüzoidal sinyaller CRO'nun hem yatay hem de dikey saptırma plakalarına uygulandığında ekranda Lissajous figürü görüntülenecektir. Bu nedenle, standart olan sinüzoidal sinyali uygulayın.known frequencyCRO'nun yatay saptırma plakalarına. Benzer şekilde, sinüzoidal sinyali uygulayın.frequency dır-dir unknown CRO'nun dikey saptırma plakalarına

$ F_ {H} $ ve $ f_ {V} $, sırasıyla CRO'nun yatay ve dikey saptırma plakalarına uygulanan sinüzoidal sinyallerin frekansları olsun. $ F_ {H} $ ile $ f_ {V} $ arasındaki ilişkimathematically aşağıda gösterildiği gibi.

$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$

Yukarıdaki ilişkiden, CRO'nun dikey saptırma plakalarına uygulanan sinüzoidal sinyalin frekansını alacağız.

$ f_ {V} = \ left (\ frac {n_ {H}} {n_ {V}} \ sağ) f_ {H} $ (Denklem 1)

Nerede,

$ n_ {H} $, yatay teğetlerin sayısıdır

$ n_ {V} $ dikey teğetlerin sayısıdır

Lissajous rakamından $ n_ {H} $ ve $ n_ {V} $ değerlerini bulabiliriz. Dolayısıyla, Denklem 1'deki $ n_ {H} $, $ n_ {V} $ ve $ f_ {H} $ değerlerini değiştirerek,$f_{V}$yani frequency of sinusoidal signal CRO'nun dikey saptırma plakalarına uygulanan.

Faz Farkının Ölçülmesi

CRO'nun hem yatay hem de dikey saptırma plakalarına sinüzoidal sinyaller uygulandığında ekranda bir Lissajous şekli görüntülenir. Bu nedenle, sahip olan sinüzoidal sinyalleri uygulayın.same amplitude and frequency CRO'nun hem yatay hem de dikey saptırma plakalarına.

Şekillerine göre birkaç Lissajous figürü için, iki sinüzoidal sinyal arasındaki faz farkını doğrudan söyleyebiliriz.

• Lissajous figürü bir straight line pozitif x ekseni ile 45 $ ^ {\ circ} $ eğimle, sonra phase differenceiki sinüzoidal sinyal arasında $ 0 ^ {\ circ} $ olacaktır. Bu, bu iki sinüzoidal sinyal arasında faz farkı olmadığı anlamına gelir.

• Lissajous figürü bir straight line pozitif x ekseni ile 135 $ ^ {\ circ} $ 'lik bir eğimle, sonra phase differenceiki sinüzoidal sinyal arasında 180 $ ^ {\ circ} $ olacaktır. Bu, bu iki sinüzoidal sinyalin faz dışı olduğu anlamına gelir.

• Lissajous figürü ise circular shape, bu durumda iki sinüzoidal sinyal arasındaki faz farkı 90 $ ^ {\ circ} $ veya $ 270 ^ {\ circ} $ olacaktır.

İki sinüzoidal sinyal arasındaki faz farkını formülleri kullanarak hesaplayabiliriz, Lissajous rakamları elliptical shape.

• Eliptik şekilli bir Lissajous figürünün eğim açısına sahip ana ekseni pozitif x ekseni ile $ 0 ^ {\ circ} $ ile $ 90 ^ {\ circ} $ arasında yer alıyorsa, sinüzoidal iki sinyal arasındaki faz farkı olacaktır.

$$ \ phi = \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ sağ) = \ sin ^ {- 1} \ left (\ frac {y_ {1} } {y_ {2}} \ sağ) $$

• Eliptik şekilli bir Lissajous figürünün eğim açısına sahip ana ekseni pozitif x ekseni ile 90 $ ^ {\ circ} $ ile $ 180 ^ {\ circ} $ arasında yer alıyorsa, sinüzoidal iki sinyal arasındaki faz farkı olacaktır.

$$ \ phi = 180 - \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180 - \ sin ^ {- 1} \ left (\ frac { y_ {1}} {y_ {2}} \ sağ) $$

Where,

$ x_ {1} $, Lissajous şeklindeki eliptik şeklin kesiştiği, başlangıçtan x eksenindeki noktaya olan mesafedir

$ x_ {2} $, eliptik şeklin Lissajous figürünün orijinden dikey tanjantına olan mesafesidir

$ y_ {1} $, başlangıçtan y ekseni üzerindeki Lissajous şeklindeki eliptik şeklin kesiştiği noktaya olan mesafedir

$ y_ {2} $, eliptik şeklin Lissajous figürünün orijinden yatay tanjantına olan mesafesidir

Bu bölümde, bilinmeyen sinüzoidal sinyalin frekansını ve Lissajous figürlerinden alınan iki sinüzoidal sinyal arasındaki faz farkını formül kullanarak nasıl bulacağımızı öğreneceğiz.

Herhangi bir test devresini bir prob aracılığıyla bir osiloskopa bağlayabiliriz. CRO temel bir osiloskop olduğu için ona bağlı olan proba da denirCRO probe.

Probu, test devresinde herhangi bir yükleme sorunu yaratmayacak şekilde seçmeliyiz. Böylece CRO ekranında test devresini sinyaller ile doğru şekilde analiz edebiliriz.

CRO probları aşağıdakilere sahip olmalıdır characteristics.

• Yüksek empedans
• Yüksek bant genişliği

block diagram CRO probu aşağıdaki şekilde gösterilmiştir.

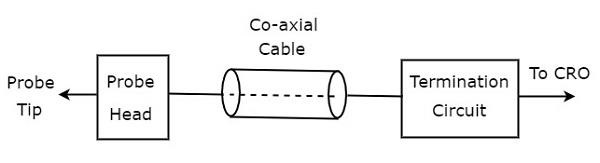
Şekilde gösterildiği gibi, CRO probu esas olarak üç bloktan oluşur. Bunlar prob kafası, koaksiyel kablo ve sonlandırma devresidir. Koaksiyel kablo, prob kafasını ve sonlandırma devresini basitçe bağlar.

CRO Problarının Türleri

CRO probları aşağıdaki şekilde sınıflandırılabilir two types.

• Pasif Problar
• Aktif Problar

Şimdi bu iki tür sondayı tek tek tartışalım.

Pasif Problar

Prob kafası pasif elemanlardan oluşuyorsa, o zaman denir passive probe. Pasif probun devre şeması aşağıdaki şekilde gösterilmiştir.

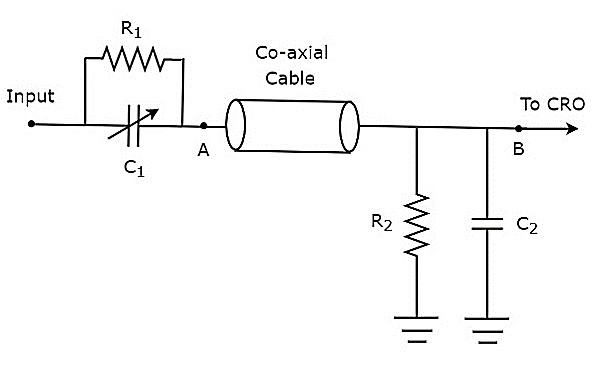
Şekilde gösterildiği gibi, prob kafası paralel bir direnç kombinasyonu, $ R_ {1} $ ve değişken bir kapasitör, $ C_ {1} $ içerir. Benzer şekilde, sonlandırma devresi paralel bir direnç, $ R_ {2} $ ve kapasitör, $ C_ {2} $ kombinasyonundan oluşur.

Yukarıdaki devre şeması şu şekilde değiştirilmiştir: bridge circuit ve aşağıdaki şekilde gösterilmiştir.

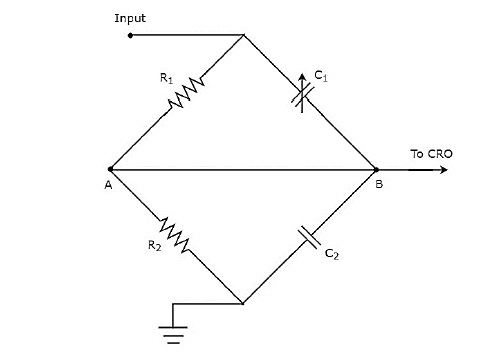
Değişken kapasitörün değerini $ c_ {1} $ ayarlayarak köprüyü dengeleyebiliriz. Sonraki bölümlerde köprü kavramını tartışacağız. Şimdilik aşağıdakileri düşününbalancing condition of AC bridge.

$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$

Substitute, empedanslar $ Z_ {1}, Z_ {2}, Z_ {3} $ ve $ Z_ {4} $ as $ R_ {1}, \ frac {1} {j \ omega C_ {1}}, R_ { Yukarıdaki denklemde sırasıyla 2} $ ve $ \ frac {1} {j \ omega C_ {2}} $.

$$ R_ {1} \ left (\ frac {1} {j \ omega C_ {2}} \ right) = \ left (\ frac {1} {j \ omega C_ {1}} \ sağ) R_ {2 } $$

$ \ Rightarrow R_ {1} C_ {1} = R_ {2} C_ {2} $ Denklem 1

Voltaj bölme prensibine göre, voltage across resistor, $R_{2}$ gibi

$$ V_ {0} = V_ {i} \ left (\ frac {R_ {2}} {R_ {1} + R_ {2}} \ sağ) $$

attenuation factorgiriş voltajı, $ V_ {i} $ ve çıkış voltajının, $ V_ {0} $ oranıdır. Yani, yukarıdaki denklemden zayıflama faktörünü, $ \ alpha $ as

$$ \ alpha = \ frac {V_ {i}} {V_ {0}} = \ frac {R_ {1} + R_ {2}} {R_ {2}} $$

$ \ Rightarrow \ alpha = 1+ \ frac {R_ {1}} {R_ {2}} $

$ \ Rightarrow \ alpha-1 = \ frac {R_ {1}} {R_ {2}} $

$ \ Rightarrow R_ {1} = \ left (\ alpha-1 \ right) R_ {2} $ Denklem 2

Denklem 2'den, $ \: \ alpha> 1 $ tamsayı değerleri için $ R_ {1} $ değerinin ð ?? '… 2 değerinden büyük veya ona eşit olduğu sonucuna varabiliriz.

Denklem 1'deki İkame Denklem 2.

$$ \ left (\ alpha-1 \ sağ) R_ {2} C_ {1} = R_ {2} C_ {2} $$

$ \ Rightarrow \ left (\ alpha-1 \ right) C_ {1} = C_ {2} $

$ \ Rightarrow C_ {1} = \ frac {C_ {2}} {\ left (\ alpha-1 \ right)} $ Denklem 3

Denklem 3'ten, $ C_ {1} $ değerinin, $ \ alpha> 1 $ tamsayı değerleri için $ C_ {2} $ değerinden küçük veya ona eşit olduğu sonucuna varabiliriz.

Example

Zayıflatma faktörü $ \ alpha $ olan bir araştırmanın $ R_ {1} $ ve $ C_ {1} $ değerlerini bulalım. $ R_ {2} = 1 M \ Omega $ ve $ C_ varsayalım. {2} = 18pF $.

• Step1 - Denklem 2'deki $ \ alpha $ ve $ R_ {2} $ değerlerini değiştirerek $ R_ {1} $ değerini alacağız.

$$ R_ {1} = \ left (10-1 \ right) \ times 1 \ times 10 ^ {6} $$

$$ \ Rightarrow R_ {1} = 9 \ times 10 ^ {6} $$

$$ \ Rightarrow R_ {1} = 9 M \ Omega $$

Step 2 - Denklem 3'teki $ \ alpha $ ve $ C_ {2} $ değerlerini değiştirerek $ C_ {1} $ değerini alacağız.

$$ C_ {1} = \ frac {18 \ times10 ^ {- 12}} {\ left (10-1 \ right)} $$

$$ \ Rightarrow C_ {1} = 2 \ times 10 ^ {- 12} $$

$$ \ Rightarrow C_ {1} = 2 pF $$

Bu nedenle, bir araştırmanın $ R_ {1} $ ve $ C_ {1} $ değerleri verilen özellikler için sırasıyla $ 9M \ Omega $ ve $ 2pF $ olacaktır.

Aktif Problar

Prob kafası aktif elektronik bileşenlerden oluşuyorsa buna denir active probe. Aktif probun blok şeması aşağıdaki şekilde gösterilmiştir.

Şekilde gösterildiği gibi, prob kafası BJT yayıcı takipçisi ile kademeli olarak bir FET kaynak takipçisinden oluşur. FET kaynak takipçisi, yüksek giriş empedansı ve düşük çıkış empedansı sağlar. Oysa BJT emitör takipçisinin amacı, empedans uyumsuzluğunu önlemek veya ortadan kaldırmaktır.

Koaksiyel kablo ve sonlandırma devresi gibi diğer iki parça hem aktif hem de pasif problarda aynı kalır.

Elektrik bileşenleri bir köprü veya halka yapısı şeklinde düzenlenmişse, bu elektrik devresine bir bridge. Genel olarak, köprü dört kol veya daldan oluşan bir döngü oluşturur. Her dal bir veya iki elektrikli bileşen içerebilir.

Köprü Türleri

Köprü devrelerini veya köprüleri, çalıştırılabilecekleri voltaj sinyaline göre aşağıdaki iki kategoriye ayırabiliriz.

• DC Köprüler
• AC Köprüleri

Şimdi kısaca bu iki köprüyü tartışalım.

DC Köprüler

Köprü devresi yalnızca DC voltaj sinyali ile çalıştırılabiliyorsa, bu bir DC köprü devresidir veya basitçe DC bridge. Bilinmeyen direncin değerini ölçmek için DC köprüler kullanılır. circuit diagram DC köprüsü aşağıdaki şekilde gösterildiği gibidir.

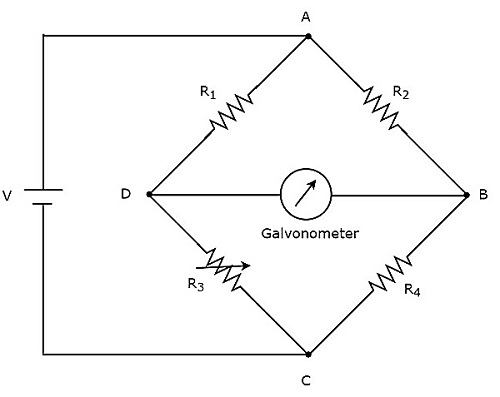
Yukarıdaki DC köprüsünde four armsve her kol bir dirençten oluşur. Bunların arasında iki direnç sabit direnç değerlerine sahip, bir direnç değişken bir direnç, diğeri ise bilinmeyen bir direnç değerine sahip.

Yukarıdaki DC köprü devresi, bir DC voltage sourcebir köşegen yerleştirerek. Galvanometre, DC köprüsünün diğer köşegenine yerleştirilir. Köprü dengesiz olduğu sürece bir miktar sapma gösterir.

Galvanometre sıfır (sıfır) sapma gösterene kadar değişken direncin direnç değerini değiştirin. Şimdi, yukarıdaki DC köprüsünün dengeli olduğu söyleniyor. Böylece, değerini bulabilirizunknown resistance düğüm denklemlerini kullanarak.

AC Köprüleri

Köprü devresi sadece AC voltaj sinyali ile çalıştırılabiliyorsa, o zaman AC köprü devresi olduğu veya basitçe olduğu söylenir. AC bridge. AC köprüler, bilinmeyen endüktans, kapasitans ve frekansın değerini ölçmek için kullanılır.

circuit diagram AC köprüsü aşağıdaki şekilde gösterildiği gibidir.

AC köprüsünün devre şeması, DC köprüsüne benzer. Yukarıdaki AC köprüsündefour armsve her kol bir miktar empedanstan oluşur. Bu, her bir kolun direnç, indüktör ve kondansatör gibi pasif elemanların tekli veya kombinasyonuna sahip olacağı anlamına gelir.

Dört empedans arasında, iki empedans sabit değerlere sahiptir, bir empedans değişkendir ve diğeri bilinmeyen bir empedanstır.

Yukarıdaki AC köprü devresi, bir AC voltage sourcebir köşegen yerleştirerek. AC köprüsünün diğer köşegenine bir dedektör yerleştirilir. Köprü dengesiz olduğu sürece bir miktar sapma gösterir.

Yukarıdaki AC köprü devresi, bir AC voltage sourcebir köşegen yerleştirerek. AC köprüsünün diğer köşegenine bir dedektör yerleştirilir. Köprü dengesiz olduğu sürece bir miktar sapma gösterir.

Detektör boş (sıfır) sapma gösterene kadar değişken empedansın empedans değerini değiştirin. Şimdi, yukarıdaki AC köprüsünün dengeli olduğu söyleniyor. Böylece, değerini bulabilirizunknown impedance dengeli koşul kullanarak.

DC bridgessadece DC voltaj sinyali ile çalıştırılabilir. DC köprüler, köprüde bulunan bilinmeyen direncin değerini ölçmek için kullanışlıdır. Wheatstone's Bridge, DC köprüsünün bir örneğidir.

Şimdi konuşalım Wheatstone’s Bridge bilinmeyen direncin değerini bulmak için.

Wheatstone Köprüsü

Wheatstone'un köprüsü, temelde dört kolu olan basit bir DC köprüsüdür. Bu dört kol eşkenar dörtgen veya kare bir şekil oluşturur ve her kol bir dirençten oluşur.

Bilinmeyen direncin değerini bulmak için galvanometreye ve DC voltaj kaynağına ihtiyacımız var. Dolayısıyla, bu ikisinden biri Wheatstone köprüsünün bir köşegenine, diğeri ise Wheatstone köprüsünün başka bir köşegenine yerleştirilir.

Wheatstone'un köprüsü, orta direncin değerini ölçmek için kullanılır. circuit diagram Wheatstone köprüsünün görünümü aşağıdaki şekilde gösterilmiştir.

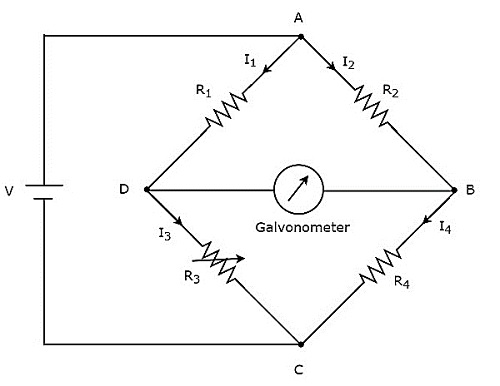
Yukarıdaki devrede, AB, BC, CD ve DA kolları birlikte bir rhombusveya kare şekli. Sırasıyla $ R_ {2} $, $ R_ {4} $, $ R_ {3} $ ve $ R_ {1} $ dirençlerinden oluşurlar. Bu direnç kollarından geçen akım sırasıyla $ I_ {2} $, $ I_ {4} $, $ I_ {3} $ ve $ I_ {1} $ olsun ve bu akımların yönleri şekilde gösterilsin.

Diyagonal kollar DB ve AC, sırasıyla galvanometre ve V voltluk DC voltaj kaynağından oluşur. Burada direnç, $ R_ {3} $ standart bir değişken dirençtir ve direnç, $ R_ {4} $ bilinmeyen bir dirençtir. Yapabilirizbalance the bridge, direncin direnç değerini değiştirerek, $ R_ {3} $.

Yukarıdaki köprü devresi, diyagonal kol DB'den hiçbir akım geçmediğinde dengelenir. Yani varno deflection galvanometrede, köprü dengelendiğinde.

Aşağıdaki durumlarda köprü dengelenecektir two conditions tatmin edici.

• AD kolundaki voltaj, AB kolundaki voltaja eşittir. yani

$$ V_ {AD} = V_ {AB} $$

$ \ Rightarrow I_ {1} R_ {1} = I_ {2} R_ {2} $ Denklem 1

• DC kolundaki voltaj, BC kolundaki voltaja eşittir. yani

$$ V_ {DC} = V_ {BC} $$

$ \ Rightarrow I_ {3} R_ {3} = I_ {4} R_ {4} $ Denklem 2

Yukarıdaki iki dengeleme koşulundan aşağıdakileri alacağız two conclusions.

• AD kolundan geçen akım, DC kolununkine eşit olacaktır. yani

$$ I_ {1} = I_ {3} $$

• AB kolundan geçen akım BC kolununkine eşit olacaktır. yani

$$ I_ {2} = I_ {4} $$

Denklem 1 ve Denklem 2'nin oranını alın.

$ \ frac {I_ {1} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {2} R_ {2}} {I_ {4} R_ {4}} $ Denklem 3

Denklem 3'te yerine, $ I_ {1} = I_ {3} $ ve $ I_ {2} = I_ {4} $.

$$ \ frac {I_ {3} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {4} R_ {2}} {I_ {4} R_ {4}} $$

$$ \ Rightarrow \ frac {R_ {1}} {R_ {3}} = \ frac {R_ {2}} {R_ {4}} $$

$$ \ Rightarrow R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$

Yukarıdaki denklemde dirençlerin bilinen değerlerini $ R_ {1} $, $ R_ {2} $ ve $ R_ {3} $ değiştirerek, value of resistor,$R_{4}$.

Bu bölümde, endüktansı ölçmek için kullanılabilecek AC köprülerinden bahsedelim. AC köprüleri yalnızca AC voltaj sinyali ile çalışır. circuit diagram AC köprüsü aşağıdaki şekilde gösterilmiştir.

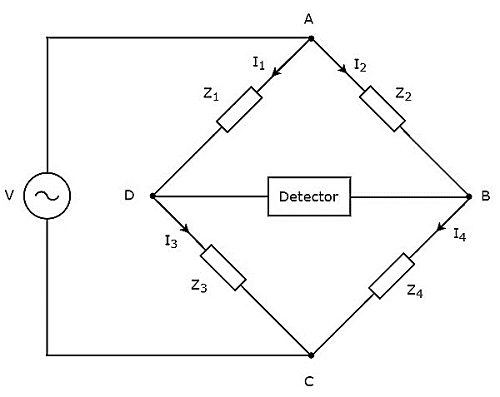
Yukarıdaki şekilde gösterildiği gibi, AC köprüsü esas olarak eşkenar dörtgen şeklinde birbirine bağlanan dört koldan oluşur veya square shape. Bütün bu kollar bir miktar empedanstan oluşur.

Bilinmeyen empedans değerini bulmak için dedektör ve AC voltaj kaynağı da gereklidir. Dolayısıyla, bu ikisinden biri AC köprüsünün bir köşegenine, diğeri ise AC köprüsünün diğer köşegenine yerleştirilir. Wheatstone köprüsünün dengeleme durumu -

$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$

Alacağız balancing condition of AC bridge, sadece yukarıdaki denklemde R'yi Z ile değiştirerek.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$ \ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $

Burada, $ Z_ {1} $ ve $ Z_ {2} $ sabit empedanslardır. Oysa $ Z_ {3} $, standart bir değişken empedanstır ve $ Z_ {4} $ bilinmeyen bir empedanstır.

Note - Uygulamaya bağlı olarak, bu dört empedansın herhangi ikisini sabit empedans, bir empedans standart değişken empedans ve diğer empedans bilinmeyen empedans olarak seçebiliriz.

Aşağıdakiler, ölçmek için kullanılabilecek iki AC köprüsüdür. inductance.

• Maxwell Köprüsü
• Hay's Bridge

Şimdi bu iki AC köprüsünü tek tek tartışalım.

Maxwell Köprüsü

Maxwell köprüsü, eşkenar dörtgen şeklinde birbirine bağlanan dört kolu olan bir AC köprüsüdür veya square shape. Bu köprünün iki kolu tek bir dirençten oluşur, bir kol bir dizi direnç ve indüktör kombinasyonundan oluşur ve diğer kol, direnç ve kapasitörün paralel bir kombinasyonundan oluşur.

Bilinmeyen empedansın değerini bulmak için bir AC dedektörü ve AC voltaj kaynağı kullanılır. Dolayısıyla, bu ikisinden biri Maxwell köprüsünün bir köşegenine, diğeri de Maxwell köprüsünün diğer köşegenine yerleştirilir.

Maxwell köprüsü, orta endüktans değerini ölçmek için kullanılır. circuit diagram Maxwell köprüsü aşağıdaki şekilde gösterilmiştir.

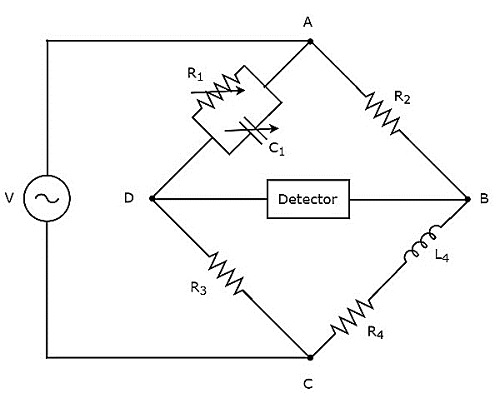
Yukarıdaki devrede, AB, BC, CD ve DA kolları birlikte eşkenar dörtgen veya kare bir şekil oluşturur. AB ve CD kolları sırasıyla $ R_ {2} $ ve $ R_ {3} $ dirençlerinden oluşur. BC kolu, bir dizi direnç, $ R_ {4} $ ve indüktör, $ L_ {4} $ kombinasyonundan oluşur. DA kolu, paralel bir direnç, $ R_ {1} $ ve kapasitör, $ C_ {1} $ kombinasyonundan oluşur.

Diyelim ki $ Z_ {1}, Z_ {2}, Z_ {3} $ ve $ Z_ {4} $ sırasıyla DA, AB, CD ve BC kollarının empedansları olsun. values of these impedances olacak

$$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$

$$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$

$ Z_ {2} = R_ {2} $

$ Z_ {3} = R_ {3} $

$ Z_ {4} = R_ {4} + j \ omega L_ {4} $

Substitute AC köprüsünün aşağıdaki dengeleme koşulundaki bu empedans değerleri.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ sağ)} $$

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}} $

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} $

Tarafından comparing Yukarıdaki denklemin ilgili gerçek ve hayali terimlerini alacağız

$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $ Denklem 1

$ L_ {4} = C_ {1} R_ {2} R_ {3} $ Denklem 2

Denklem 1'de $ R_ {1} $, $ R_ {2} $ ve $ R_ {3} $ dirençlerinin değerlerini değiştirerek, direnç değerini $ R_ {4} $ alacağız. Benzer şekilde, Denklem 2'deki kapasitör değeri $ C_ {1} $ ve dirençlerin değerleri $ R_ {2} $ ve $ R_ {3} $ yerine kondüktörün değeri $ L_ {4 } $.

advantage Maxwell köprüsünün her ikisi de direnç değerinin, $ R_ {4} $ ve bir indüktörün, $ L_ {4} $ değerinin frekans değerinden bağımsız olmasıdır.

Hay's Bridge

Hay'in köprüsü, Maxwell köprüsünde bir dizi direnç ve kapasitör kombinasyonundan oluşan kola paralel bir direnç ve kapasitör kombinasyonundan oluşan kolu değiştirerek elde ettiğimiz Maxwell köprüsünün değiştirilmiş bir versiyonudur.

Hay'in köprüsü, yüksek endüktans değerini ölçmek için kullanılır. circuit diagram Hay's Köprüsü'nün görünümü aşağıdaki şekilde gösterilmiştir.

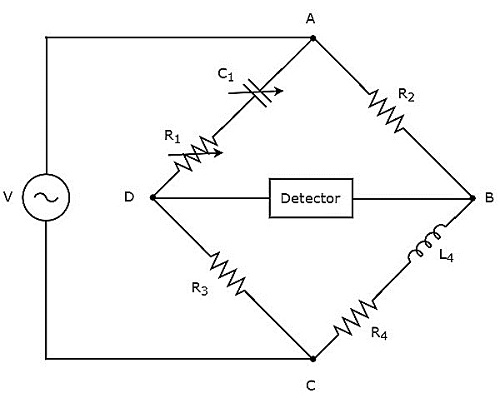
Yukarıdaki devrede, AB, BC, CD ve DA kolları birlikte eşkenar dörtgen veya kare bir şekil oluşturur. Kollar, AB ve CD, sırasıyla $ R_ {2} $ ve $ R_ {3} $ dirençlerinden oluşur. BC kolu, bir dizi direnç, $ R_ {4} $ ve indüktör, $ L_ {4} $ kombinasyonundan oluşur. DA kolu, bir dizi direnç, $ R_ {1} $ ve kapasitör, $ C_ {1} $ kombinasyonundan oluşur.

Diyelim ki $ Z_ {1}, Z_ {2}, Z_ {3} $ ve $ Z_ {4} $ sırasıyla DA, AB, CD ve BC kollarının empedansları olsun. values of these impedances olacak

$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$

$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $

$ Z_ {2} = R_ {2} $

$ Z_ {3} = R_ {3} $

$ Z_ {4} = R_ {4} + j \ omega L_ {4} $

Substitute AC köprüsünün aşağıdaki dengeleme koşulundaki bu empedans değerleri.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ sağ)} $

$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ sağ)} $

Yukarıdaki denklemde sağ taraftaki terimin payını ve paydasını $ 1 - j \ omega R_ {1} C_ {1} $ ile çarpın.

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ sağ)} \ times \ frac {\ left (1 - j \ omega R_ {1} C_ {1} \ right)} {\ left (1 - j \ omega R_ {1} C_ {1} \ sağ )} $

$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ omega R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ sağ)} $

Tarafından comparing Yukarıdaki denklemin ilgili gerçek ve hayali terimlerini alacağız

$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ sağ)} $ Denklem 3

$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ sağ)} $ Denklem 4

Denklem 3 ve Denklem 4'teki $ R_ {1}, R_ {2}, R_ {3}, C_ {1} $ ve $ \ omega $ değerlerini değiştirerek, direnç, $ R_ {4 değerlerini alacağız } $ ve indüktör, $ L_ {4} $.

Önceki bölümde, endüktansı ölçmek için kullanılabilecek iki AC köprüsünden bahsetmiştik. Bu bölümde aşağıdakileri tartışalımtwo AC bridges.

• Schering Köprüsü
• Wien Köprüsü

Bu iki köprü, sırasıyla kapasitans ve frekansı ölçmek için kullanılabilir.

Schering Köprüsü

Schering köprüsü, eşkenar dörtgen şeklinde birbirine bağlanan dört kolu olan bir AC köprüsüdür veya square shapebir kolu tek bir dirençten, bir kolu bir dizi direnç ve kondansatör kombinasyonundan, bir kolu tek bir kapasitörden ve diğer kol ise direnç ve kapasitörün paralel bir kombinasyonundan oluşur.

AC detektörü ve AC voltaj kaynağı da bilinmeyen empedansın değerini bulmak için kullanılır, bu nedenle bunlardan biri Schering köprüsünün bir köşegenine ve diğeri Schering köprüsünün diğer köşegenine yerleştirilir.

Schering köprüsü, kapasitans değerini ölçmek için kullanılır. circuit diagram Schering köprüsü aşağıdaki şekilde gösterilmiştir.

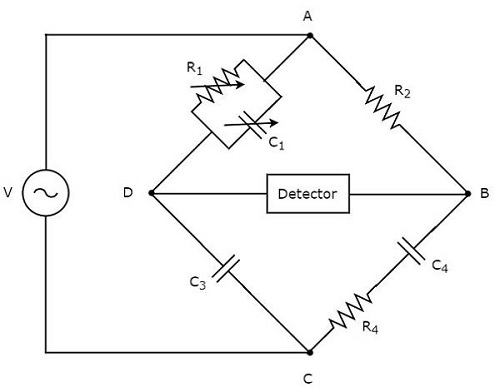
Yukarıdaki devrede, AB, BC, CD ve DA kolları birlikte bir eşkenar dörtgen oluşturur veya square shape. AB kolu bir dirençten oluşur, $ R_ {2} $. BC kolu, bir dizi direnç, $ R_ {4} $ ve kapasitör, $ C_ {4} $ kombinasyonundan oluşur. Kol CD'si bir kapasitör $ C_ {3} $ içerir. DA kolu, paralel bir direnç, $ R_ {1} $ ve kapasitör $ C_ {1} $ kombinasyonundan oluşur.

Diyelim ki $ Z_ {1} $, $ Z_ {2} $, $ Z_ {3} $ ve $ Z_ {4} $ sırasıyla DA, AB, CD ve BC kollarının empedansları olsun. values of these impedances olacak

$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $

$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $

$ Z_ {2} = R_ {2} $

$ Z_ {3} = \ frac {1} {j \ omega C_ {3}} $

$ Z_ {4} = R_ {4} + \ frac {1} {j \ omega C_ {4}} $

$ \ Rightarrow Z_ {4} = \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} $

Substitute AC köprüsünün aşağıdaki dengeleme koşulundaki bu empedans değerleri.

$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$

$$ \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (\ frac {1} {j \ omega C_ { 3}} \ sağ)} {\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} $$

$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ sağ)} {j \ omega R_ {1} C_ {3}} $

$ \ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ sağ)} {R_ {1} C_ {3}} $

$ \ Rightarrow \ frac {1} {C_ {4}} + j \ omega R_ {4} = \ frac {R_ {2}} {R_ {1} C_ {3}} + \ frac {j \ omega C_ { 1} R_ {2}} {C_ {3}} $

Tarafından comparing Yukarıdaki denklemin ilgili gerçek ve hayali terimlerini alacağız

$ C_ {4} = \ frac {R_ {1} C_ {3}} {R_ {2}} $ Denklem 1

$ R_ {4} = \ frac {C_ {1} R_ {2}} {C_ {3}} $ Denklem 2

Denklem 1'deki $ R_ {1}, R_ {2} $ ve $ C_ {3} $ değerlerini değiştirerek, $ C_ {4} $ kapasitörünün değerini alacağız. Benzer şekilde, Denklem 2'de $ R_ {2}, C_ {1} $ ve $ C_ {3} $ değerlerini değiştirerek, direncin değeri $ R_ {4} $ alacağız.

advantage Schering köprüsünün her iki değeri, $ R_ {4} $ ve kapasitör, $ C_ {4} $ değerlerinin frekans değerinden bağımsız olmasıdır.

Wien Köprüsü

Wien’s bridgeeşkenar dörtgen veya kare şeklinde birbirine bağlanan dört kolu olan bir AC köprüsüdür. İki kol arasında tek bir direnç, bir kol direnç ve kapasitörün paralel bir kombinasyonundan oluşur ve diğer kol bir dizi direnç ve kondansatör kombinasyonundan oluşur.

Frekans değerini bulmak için AC detektörü ve AC voltaj kaynağı da gereklidir. Dolayısıyla bu ikisinden biri Viyana köprüsünün bir köşegenine, diğeri ise Viyana köprüsünün diğer köşegenine yerleştirilir.

circuit diagram Wien köprüsünün bir kısmı aşağıdaki şekilde gösterilmiştir.

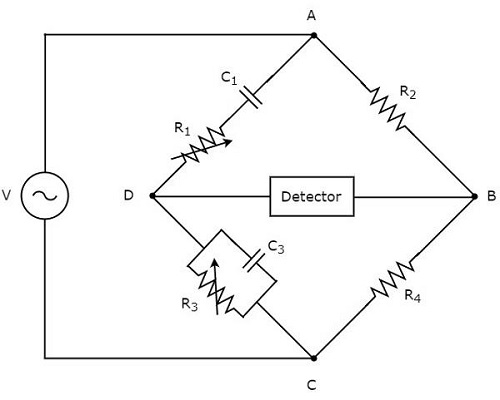
Yukarıdaki devrede, AB, BC, CD ve DA kolları birlikte bir eşkenar dörtgen oluşturur veya square shape. Kollar, AB ve BC sırasıyla $ R_ {2} $ ve $ R_ {4} $ dirençlerinden oluşur. Kol, CD, paralel bir direnç, $ R_ {3} $ ve kapasitör, $ C_ {3} $ kombinasyonundan oluşur. DA kolu, bir dizi direnç, $ R_ {1} $ ve kapasitör, $ C_ {1} $ kombinasyonundan oluşur.

Diyelim ki $ Z_ {1}, Z_ {2}, Z_ {3} $ ve $ Z_ {4} $ sırasıyla DA, AB, CD ve BC kollarının empedansları olsun. values of these impedances olacak

$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$

$$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $$

$ Z_ {2} = R_ {2} $

$$ Z_ {3} = \ frac {R_ {3} \ left (\ frac {1} {j \ omega C_ {3}} \ right)} {R_ {3} + \ frac {1} {j \ omega C_ {3}}} $$

$$ \ Rightarrow Z_ {3} = \ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} $$

$ Z_ {4} = R_ {4} $

Substitute AC köprüsünün aşağıdaki dengeleme koşulundaki bu empedans değerleri.

$$ Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $$

$$ \ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ sağ) R_ {4} = R_ {2} \ left (\ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} \ sağ) $$

$ \ Rightarrow \ left (1 + j \ omega R_ {1} C_ {1} \ right) \ left (1 + j \ omega R_ {3} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $

$ \ Rightarrow \ left (1 + j \ omega R_ {3} C_ {3} + j \ omega R_ {1} C_ {1} - \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ sağ) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3} $

$ \ Rightarrow R_ {4} \ left (\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ sağ) + j \ omega R_ {4} \ left (R_ {3} C_ {3} + R_ {1} C_ {1} \ sağ) = j \ omega C_ {1} R_ {2} R_ {3} $

Equate ilgili real terms Yukarıdaki denklemin.

$$ R_ {4} \ left (1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ sağ) = 0 $$

$ \ Rightarrow 1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} = 0 $

$ \ Rightarrow 1 = \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} $

$ \ omega = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $

Substitute, $ \ omega = 2 \ pi f $ yukarıdaki denklemde.

$$ \ Rightarrow 2 \ pi f = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $$

$ \ Rightarrow f = \ frac {1} {2 \ pi \ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}} $

Yukarıdaki denklemde $ R_ {1}, R_ {3}, C_ {1} $ ve $ C_ {3} $ değerlerini değiştirerek AC gerilim kaynağının frekans değerini, $ f $ değerini bulabiliriz.

Eğer $ R_ {1} = R_ {3} = R $ ve $ C_ {1} = C_ {3} = C $ ise, aşağıdaki formülü kullanarak AC gerilim kaynağının $ f $ frekans değerini bulabiliriz .

$$ f = \ frac {1} {2 \ pi RC} $$

Wein'in köprüsü esas olarak frequency value AF aralığı.

Temel olarak, Dönüştürücü bir enerji biçimini başka bir enerji biçimine dönüştürür. Elektriksel olmayan enerji biçimini elektriksel enerji biçimine dönüştüren dönüştürücü,electrical transducer. block diagram Elektrik dönüştürücüsünün oranı aşağıdaki şekilde gösterilmiştir.

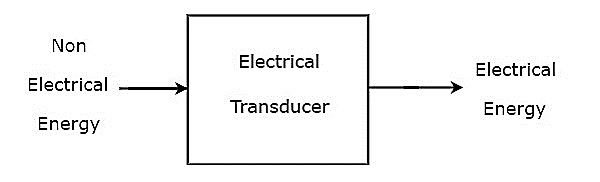
Şekilde gösterildiği gibi, elektrik dönüştürücü, elektrik enerjisine sahip bir çıktı üretecektir. Elektrik dönüştürücünün çıkışı, elektriksel olmayan enerjiye sahip olan girişe eşdeğerdir.

Elektrik Dönüştürücü Türleri

Temel olarak, elektrik dönüştürücüler aşağıdaki şekilde sınıflandırılabilir: two types.

• Aktif Dönüştürücüler
• Pasif Dönüştürücüler

Şimdi kısaca bu iki tip dönüştürücüden bahsedelim.

Aktif Dönüştürücüler

Voltaj ve akım gibi elektriksel büyüklüklerden birini üretebilen transdüser, active transducer. Herhangi bir harici güç kaynağı gerektirmediği için kendi kendini üreten dönüştürücü olarak da adlandırılır.

block diagram Aktif dönüştürücünün oranı aşağıdaki şekilde gösterilmiştir.

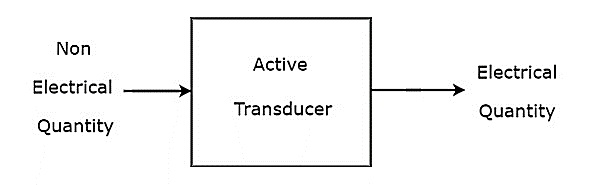
Şekilde gösterildiği gibi, aktif dönüştürücü, elektriksel olmayan giriş miktarına (veya sinyaline) eşdeğer olan bir elektriksel nicelik (veya sinyal) üretecektir.

Examples

Aşağıda aktif dönüştürücülerin örnekleri verilmiştir.

• Piezo Elektrik Dönüştürücü
• Fotoğraf Elektrik Dönüştürücü
• Termo Elektrik Dönüştürücü

Bir sonraki bölümde bu aktif dönüştürücüler hakkında tartışacağız.

Pasif Dönüştürücüler

Voltaj ve akım gibi elektriksel büyüklükleri üretemeyen transdüser, passive transducer. Ancak direnç (R), indüktör (L) ve kapasitör (C) gibi pasif elemanlardan birinde varyasyon üretir. Pasif dönüştürücü, harici güç kaynağı gerektirir.

block diagram Pasif dönüştürücü aşağıdaki şekilde gösterilmektedir.

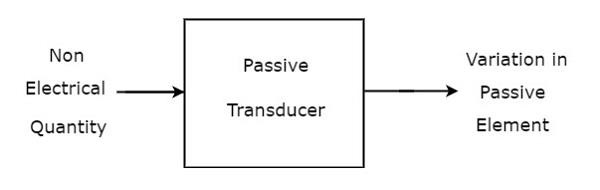
Şekilde gösterildiği gibi, pasif dönüştürücü, elektriksel olmayan giriş miktarındaki (veya sinyaldeki) varyasyona göre pasif elemanda varyasyon üretecektir.

Examples

Aşağıda pasif dönüştürücülerin örnekleri verilmiştir.

• Dirençli Dönüştürücü
• Endüktif Dönüştürücü
• Kapasitif Dönüştürücü

Sonraki bölümlerde bu pasif dönüştürücüler hakkında tartışacağız.

Active transducerelektriksel olmayan miktarı elektriksel bir miktara dönüştüren bir dönüştürücüdür. Basınç, ışık aydınlatması ve sıcaklık gibi elektriksel olmayan nicelikleri ele alalım. Bu nedenle, seçtiğimiz elektriksel olmayan miktara bağlı olarak aşağıdaki üç aktif dönüştürücüyü alacağız.

• Piezo Elektrik Dönüştürücü
• Fotoğraf Elektrik Dönüştürücü
• Termo Elektrik Dönüştürücü

Şimdi bu üç aktif dönüştürücüyü tek tek tartışalım.

Piezo Elektrik Dönüştürücü

Aktif bir dönüştürücü olduğu söyleniyor piezo electric transducer, basınç girdisine eşdeğer bir elektriksel miktar ürettiğinde. Aşağıdaki üç madde piezo elektrik etkisi gösterir.

• Quartz
• Rochelle tuzları
• Tourmaline

Bu üç maddenin sergilediği piezo-elektrik etkisi, bu artan sırada Turmalin, Kuvars ve Rochelle tuzlarıdır. Bu üç maddenin sahip olduğu artan mekanik mukavemet sırası, Rochelle tuzları, Kuvars, Turmalindir.

Quartz ılımlı piezo elektrik etkisi sergilediğinden ve bu üç piezo elektrik maddesi arasında orta derecede mekanik mukavemete sahip olduğundan piezo elektrik dönüştürücü olarak kullanılır.

Kuvars Dönüştürücü

circuit diagramKuvars dönüştürücü aşağıdaki şekilde gösterilmektedir. Şekilde görüldüğü gibi, kuvars kristali taban ve kuvvet toplama elemanı arasına yerleştirilmiştir. Çıkış voltajı, kuvars kristalinin iki tarafına yerleştirilmiş metal elektrotlar boyunca ölçülebilir.

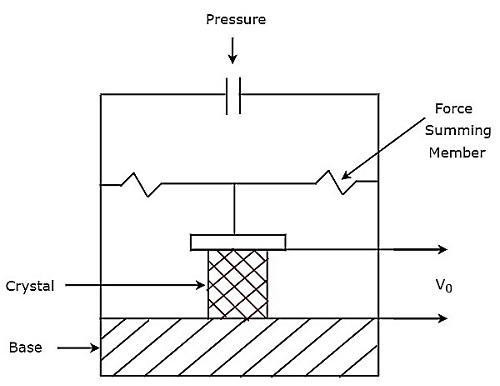
output voltage, $ V_ {0} $ üzerindeki basınç dönüştürücü

$$ V_ {0} = \ frac {Q} {C} $$

Fotoğraf Elektrik Dönüştürücü

Aktif bir güç çeviricinin, ışık girişinin aydınlatılmasına eşdeğer bir elektriksel miktar ürettiğinde, fotoelektrik dönüştürücü olduğu söylenir. circuit diagram Aşağıdaki şekilde foto elektrik dönüştürücüsü gösterilmektedir.

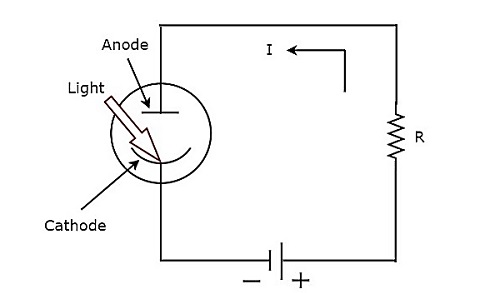
working foto elektrik dönüştürücüsü aşağıda belirtilmiştir.

• Step1 - Foto elektrik dönüştürücüsü, ışık katotunun üzerine düştüğünde elektronları serbest bırakır.

• Step2 - Foto elektrik dönüştürücüsü, elektronların anoda çekilmesi nedeniyle devrede bir akım I üretir.

Bulabiliriz sensitivity Aşağıdaki formülü kullanarak fotoğraf elektrik dönüştürücüsünün

$$ S = \ frac {I} {i} $$

Nerede,

$ S $, fotoelektrik dönüştürücünün hassasiyetidir

$ I $, fotoelektrik dönüştürücünün çıkış akımıdır

$ i $, fotoelektrik dönüştürücünün ışık girişinin aydınlatmasıdır

Termo Elektrik Dönüştürücü

Aktif bir dönüştürücü olduğu söyleniyor thermo electric transducer, sıcaklık girdisine eşdeğer bir elektriksel miktar ürettiğinde. Aşağıdaki iki dönüştürücü, termoelektrik dönüştürücü örnekleridir.

• Termistör Dönüştürücü
• Termokupl Dönüştürücü

Şimdi bu iki transdüseri tek tek tartışalım.

Termistör Dönüştürücü

Sıcaklığa bağlı olan dirence termal direnç denir. Kısacası denirThermistor. Termistörün sıcaklık katsayısı negatiftir. Bu, sıcaklık arttıkça termistörün direncinin azalması anlamına gelir.

Mathematicallytermistör direnci ile sıcaklık arasındaki ilişki şu şekilde temsil edilebilir:

$$ R_ {1} = R_ {2} e ^ \ left (\ beta \ left [\ frac {1} {T_ {1}} - \ frac {1} {T_ {2}} \ sağ] \ sağ) $$

Where,

$ R_ {1} $, termistörün $ {T_ {1}} ^ {0} K $ sıcaklığındaki direncidir

$ R_ {2} $, termistörün $ {T_ {2}} ^ {0} K $ sıcaklığındaki direncidir

$ \ beta $ sıcaklık sabiti

advantage Termistör dönüştürücü, hızlı ve kararlı bir yanıt üretecek olmasıdır.

Termokupl Dönüştürücü

Termokupl dönüştürücü, girişte karşılık gelen bir sıcaklık değişikliği için bir çıkış voltajı üretir. İki bağlantı noktası oluşturmak için farklı metallerden iki tel bir araya getirilirse, bu konfigürasyonun tamamı denirThermocouple. Temel termokuplun devre şeması aşağıda gösterilmiştir -

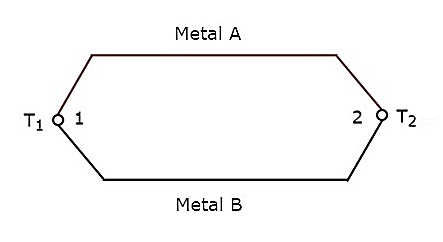
Yukarıdaki ısıl çift, iki metal, A & B ve iki bağlantı, 1 ve 2'ye sahiptir. Sabit bir referans sıcaklığı, $ T_ {2} $ bağlantı 2'de düşünün. Bağlantı noktasındaki sıcaklığın 1 $ T_ {1} $ olmasına izin verin. Termokupl, biremf (elektro motivasyon kuvveti), $ T_ {1} $ ve $ T_ {2} $ değerleri farklı olduğunda.

Bu, termokuplun, iki kavşak 1 ve 2 arasında bir sıcaklık farkı olduğunda bir emf oluşturduğu ve bu iki bağlantı arasındaki sıcaklık farkıyla doğrudan orantılı olduğu anlamına gelir. Mathematicallyşu şekilde temsil edilebilir:

$$ e \ alpha \ left (T_ {1} -T_ {2} \ sağ) $$

Nerede,

$ e $, termokupl tarafından üretilen emf'dir

Yukarıdaki termokupl devresi, pratik uygulamalar için aşağıdaki şekilde gösterildiği gibi gösterilebilir.

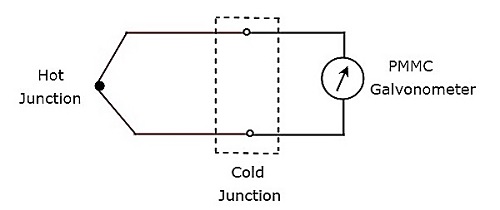
Devrenin, bu iki bağlantı dahil olmak üzere sıcak ve soğuk bağlantılar arasında kalan kısmı, eşdeğer bir temel termokupl modelidir. Soğuk bağlantıya bir PMMC galvanometre bağlanır ve soğuk bağlantı boyunca üretilen emf'ye göre saptırır.Thermocouple transducer en yaygın kullanılan termoelektrik dönüştürücüdür.

passive transducerpasif elemandaki varyasyonu üreten bir dönüştürücüdür. Direnç, indüktör ve kondansatör gibi pasif unsurları ele alacağız. Dolayısıyla, seçtiğimiz pasif öğeye bağlı olarak aşağıdaki üç pasif dönüştürücüyü alacağız.

• Dirençli Dönüştürücü
• Endüktif Dönüştürücü
• Kapasitif Dönüştürücü

Şimdi bu üç pasif dönüştürücüyü tek tek tartışalım.

Dirençli Dönüştürücü

Pasif bir dönüştürücünün bir resistive transducerdirenç değerinde değişim (değişim) ürettiğinde. aşağıdaki formülresistance, R metal bir iletkendir.

$$ R = \ frac {\ rho \: l} {A} $$

Nerede,

$ \ rho $, iletkenin direncidir

$ l $, iletkenin uzunluğudur

$ A $, iletkenin kesit alanıdır

Direnç değeri $ \ rho, l $ ve $ A $ olmak üzere üç parametreye bağlıdır. Böylece yapabilirizresistive transducers$ \ rho, l $ & $ A $ gibi üç parametreden birindeki varyasyona bağlıdır. Bu üç parametreden herhangi birindeki değişiklik direnç değerini değiştirir.

• Direnç, R ile doğru orantılıdır resistivitykondüktör, $ \ rho $. Dolayısıyla, iletkenin direnci, $ \ rho $ direncin değerini artırdıkça, R da artar. Benzer şekilde, iletkenin özdirenci, $ \ rho $ direnç değerini düşürdükçe, R de azalır.

• Direnç, R ile doğru orantılıdır lengthiletken, $ l $. Dolayısıyla, iletken uzunluğu, $ l $ direnç değerini artırdıkça, R de artar. Benzer şekilde, iletken uzunluğu $ l $ direnç değerini düşürdükçe, R de azalır.

• Direnç, R ile ters orantılıdır cross sectional areaKondüktörün $ A $. Dolayısıyla, iletkenin kesit alanı, $ A $ direnç değerini artırdıkça, R azalır. Benzer şekilde, iletkenin enine kesit alanı, $ A $ direnç değerini düşürdükçe, R artar.

Endüktif Dönüştürücü

Pasif bir dönüştürücünün bir inductive transducer, endüktans değerinde değişiklik (değişim) ürettiğinde. aşağıdaki formülinductance, Bir indüktörün L'si.

$ L = \ frac {N ^ {2}} {S} $ Denklem 1

Nerede,

$ N $, bobinin dönüş sayısıdır

$ S $, bobinin dönüş sayısıdır

aşağıdaki formül reluctance, S bobin.

$ S = \ frac {l} {\ mu A} $ Denklem 2

Nerede,

$ l $ manyetik devrenin uzunluğudur

$ \ mu $ çekirdeğin geçirgenliğidir

$ A $, akının aktığı manyetik devrenin alanıdır

İkame, Denklem 1'deki Denklem 2.

$$ L = \ frac {N ^ {2}} {\ left (\ frac {l} {\ mu A} \ right)} $$

$ \ Rightarrow L = \ frac {N ^ {2} \ mu A} {l} $ Denklem 3

Denklem 1 ve Denklem 3'ten, endüktans değerinin $ N, S $ ve $ \ mu $ olmak üzere üç parametreye bağlı olduğu sonucuna varabiliriz. Böylece yapabilirizinductive transducers$ N, S $ ve $ \ mu $ olmak üzere üç parametreden birindeki varyasyona bağlıdır. Çünkü bu üç parametreden herhangi birindeki değişim endüktans değerini değiştirir.

• Endüktans, L'nin karesiyle doğru orantılıdır. number of turns of coil. Yani, bobin dönüş sayısı, $ N $ endüktans değerini artırdıkça, $ L $ da artar. Benzer şekilde, bobin sarım sayısı kadar $ N $ endüktans değerini azaltırken, $ L $ da azalır.

• Endüktans, $ L $ ile ters orantılıdır reluctance of coil, S $. Dolayısıyla, bobinin isteksizliği, $ S $ endüktans değerini artırdıkça, $ L $ azalır. Benzer şekilde, bobinin isteksizliği, $ S $ endüktans değerini düşürdüğünde, $ L $ artar.

• Endüktans, L ile doğru orantılıdır permeability of core, $ \ mu $. Yani çekirdeğin geçirgenliği $ \ mu $ endüktans değerini artırdıkça, L de artar. Benzer şekilde, çekirdeğin geçirgenliği $ \ mu $ endüktans değerini düşürdükçe, L de azalmaktadır.

Kapasitif Dönüştürücü

Pasif bir dönüştürücünün bir capacitive transducerkapasitans değerinde değişiklik (değişim) ürettiğinde. aşağıdaki formülcapacitance, Paralel plaka kapasitörünün C'si.

$$ C = \ frac {\ varepsilon A} {d} $$

Nerede,

$ \ varepsilon $ geçirgenlik veya dielektrik sabitidir

$ A $, iki tabağın etkin alanıdır

$ d $ iki tabağın etkin alanıdır

Kapasitans değeri $ \ varepsilon, A $ ve $ d $ olmak üzere üç parametreye bağlıdır. Böylece yapabilirizcapacitive transducers$ \ varepsilon, A $ & $ d $ gibi üç parametreden birindeki varyasyona göre. Çünkü bu üç parametreden herhangi birindeki değişiklik kapasitans değerini değiştirir.

• Kapasitans, C ile doğru orantılıdır permittivity, $ \ varepsilon $. Dolayısıyla, geçirgenlik, $ \ varepsilon $ kapasitans değerini artırdıkça, C de artar. Benzer şekilde, geçirgenlik, $ \ varepsilon $ kapasitans değerini düşürürken, C de azalır.

• Kapasitans, C ile doğru orantılıdır effective area of two plates, A $. Dolayısıyla, iki plakanın etkin alanı, $ A $ kapasitans değerini artırdıkça, C de artar. Benzer şekilde iki levhanın efektif alanı $ A $ kapasite değerini düşürürken C de azalır.

• Kapasitans, C ile ters orantılıdır distance between two plates, $ d $. Böylece iki plaka arasındaki mesafe, $ d $ kapasitans değerini artırdıkça, C azalır. Benzer şekilde, iki plaka arasındaki mesafe, $ d $ kapasitans değerini düşürdükçe, C artar.

Bu bölümde, üç pasif dönüştürücüden bahsettik. Bir sonraki bölümde, her bir pasif dönüştürücü için bir örnek hakkında tartışalım.

physical quantitiesyer değiştirme, hız, kuvvet, sıcaklık vb. gibi tümü elektriksel olmayan büyüklüklerdir. aktif dönüştürücü, fiziksel miktarı bir elektrik sinyaline dönüştürür. Oysa pasif dönüştürücü, fiziksel miktarı pasif elemandaki varyasyona dönüştürür.

Bu nedenle, gereksinime bağlı olarak aktif dönüştürücü veya pasif dönüştürücü seçebiliriz. Bu bölümde, pasif bir dönüştürücü kullanarak yer değiştirmenin nasıl ölçüleceğini tartışalım. Düz bir çizgide bir noktadan başka bir noktaya hareket eden bir cisim, bu iki nokta arasındaki uzunluk olarak adlandırılır.displacement.

Aşağıdakilere sahibiz three passive transducers

• Dirençli Dönüştürücü
• Endüktif Dönüştürücü
• Kapasitif Dönüştürücü

Şimdi, bu üç pasif dönüştürücü ile yer değiştirme ölçümünü tek tek tartışalım.

Dirençli Dönüştürücü Kullanılarak Yer Değiştirme Ölçümü

circuit diagram Yer değiştirmeyi ölçmek için kullanılan rezistif transdüser, aşağıdaki şekilde gösterilmiştir.

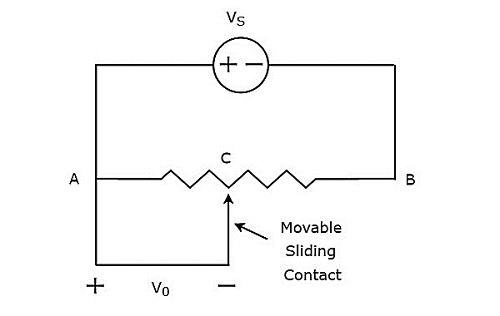
Yukarıdaki devre bir potansiyometre ve bir voltaj kaynağı, $ V_ {S} $ içerir. Bu ikisinin A ve B noktalarına göre paralel bağlandığını söyleyebiliriz. Potansiyometre, değişken olabilen kayan kontağa sahiptir. Yani C noktası değişken birdir. Yukarıdaki devrede,output voltage$ V_ {0} $, A ve C noktaları arasında ölçülür.

Mathematicallygerilimler ve mesafeler arasındaki ilişki şu şekilde temsil edilebilir:

$$ \ frac {V_ {0}} {V_ {S}} = \ frac {AC} {AB} $$

Bu nedenle, yer değiştirmesi ölçülecek gövdeyi kayan kontağa bağlamalıyız. Dolayısıyla, vücut düz bir çizgide hareket ettiğinde, C noktası da değişir. Bundan dolayı, çıkış voltajı $ V_ {0} $ da buna göre değişir.

Bu durumda, yer değiştirmeyi çıkış voltajını $ V_ {0} $ ölçerek bulabiliriz.

Endüktif Dönüştürücü Kullanılarak Yer Değiştirme Ölçümü

circuit diagram Yer değiştirmeyi ölçmek için kullanılan endüktif dönüştürücü aşağıdaki şekilde gösterilmiştir.

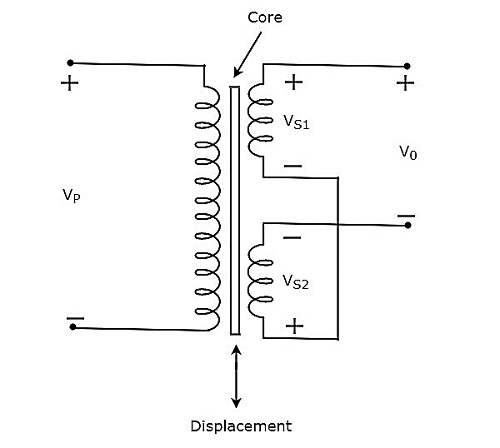
Yukarıdaki devrede bulunan transformatör, bir birincil sargı ve iki ikincil sargıya sahiptir. Burada, iki ikincil sargının bitiş noktaları birleştirilir. Yani, bu iki ikincil sargının birbirine bağlı olduğunu söyleyebiliriz.series opposition.

$ V_ {P} $ voltajı transformatörün birincil sargısına uygulanır. Her sekonder sargı boyunca gelişen voltaj ð ?? '‰ ð ??' † 1 ve ð ?? '‰ ð ??' † 2. Çıkış voltajı, $ V_ {0} $, iki ikincil sargının başlangıç ​​noktalarında alınır.

Mathematically, çıkış voltajı, ð ?? '‰ 0 olarak yazılabilir

$$ V_ {0} = V_ {S1} -V_ {S2} $$

Yukarıdaki devrede bulunan trafo denir differential transformer, bir çıkış voltajı ürettiğinden, $ V_ {S1} $ ve $ V_ {S2} $ arasındaki fark budur.

• Çekirdek merkezi konumdaysa, çıkış voltajı $ V_ {0} $ sıfıra eşit olacaktır. Çünkü, $ V_ {S1} $ ve $ V_ {S2} $ 'nın ilgili büyüklükleri ve aşamaları aynıdır.

• Çekirdek merkezi konumda değilse, çıkış voltajı, $ V_ {0} $, bir miktar büyüklük ve faza sahip olacaktır. Çünkü, $ V_ {S1} $ ve $ V_ {S2} $ 'nın ilgili büyüklükleri ve fazları eşit değildir.

Bu nedenle, yer değiştirmesi ölçülecek gövdeyi merkezi çekirdeğe bağlamalıyız. Dolayısıyla, vücut düz bir çizgide hareket ettiğinde, çekirdeğin merkezi konumu değişir. Bundan dolayı, çıkış voltajı $ V_ {0} $ da buna göre değişir.

Bu durumda, bulabiliriz displacementçıkış voltajını ölçerek, $ V_ {0} $. Çıkış voltajının büyüklüğü ve fazı, $ V_ {0} $ sırasıyla gövdenin yer değiştirmesini ve yönünü temsil eder.

Kapasitif Dönüştürücü Kullanılarak Yer Değiştirme Ölçümü

circuit diagram Yer değiştirmeyi ölçmek için kullanılan kapasitif dönüştürücü aşağıdaki şekilde gösterilmiştir.

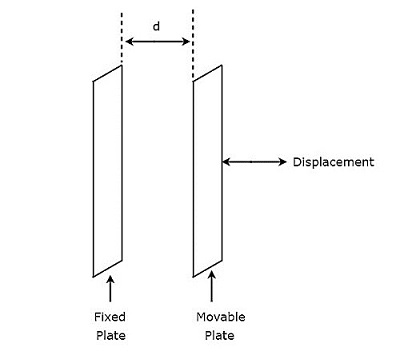
capacitorYukarıdaki devrede bulunan iki paralel plakaya sahiptir. Bunların arasında bir plaka sabit ve diğer plaka hareketli bir plakadır. Bundan dolayı, bu iki plaka arasındaki boşluk da değişecektir. Kapasitans değeri, iki kondansatör plakası arasındaki boşluk değiştikçe değişir.

Bu nedenle, vücudu birbirine bağlamalıyız. displacementbir kapasitörün hareketli plakasına ölçülecektir. Dolayısıyla, gövde düz bir çizgide hareket ettiğinde, iki kondansatör plakası arasındaki boşluk değişir. Bundan dolayı kapasitans değeri değişir.

Veri toplama için kullanılan sistemler şu şekilde bilinir: data acquisition systems. Bu veri toplama sistemleri, verilerin dönüştürülmesi, verilerin depolanması, verilerin iletilmesi ve verilerin işlenmesi gibi görevleri yerine getirecektir.

Veri toplama sistemleri aşağıdakileri dikkate alır analog signals.

• DC ve AC gerilimleri, DC ve AC akımları, direnç vb. Elektriksel büyüklüklerin doğrudan ölçülmesinden elde edilen analog sinyaller

• LVDT, Termokupl vb. Dönüştürücülerden elde edilen analog sinyaller

Veri Toplama Sistemlerinin Türleri

Veri toplama sistemleri aşağıdaki şekilde sınıflandırılabilir: two types.

• Analog Veri Toplama Sistemleri
• Sayısal Veri Toplama Sistemleri

Şimdi, bu iki tür veri toplama sistemini tek tek tartışalım.

Analog Veri Toplama Sistemleri

Analog sinyallerle çalıştırılabilen veri toplama sistemleri şu şekilde bilinir: analog data acquisition systems. Analog veri toplama sistemlerinin blokları aşağıdadır.

• Transducer - Fiziksel büyüklükleri elektrik sinyallerine çevirir.

• Signal conditioner - Sinyalin istenen kısmının yükseltilmesi ve seçilmesi gibi işlevleri yerine getirir.

• Display device - İzleme amacıyla giriş sinyallerini görüntüler.

• Graphic recording instruments - Bunlar, giriş verilerinin kalıcı olarak kaydını yapmak için kullanılabilir.

• Magnetic tape instrumentation - Giriş verilerinin alınması, depolanması ve çoğaltılması için kullanılır.

Sayısal Veri Toplama Sistemleri

Dijital sinyaller ile çalıştırılabilen veri toplama sistemleri, digital data acquisition systems. Bu nedenle, bilgileri depolamak veya görüntülemek için dijital bileşenler kullanırlar.

Esas olarak aşağıdaki operations dijital veri toplamada yer alır.

• Analog sinyallerin edinimi
• Analog sinyallerin dijital sinyallere veya dijital verilere dönüştürülmesi
• Dijital sinyallerin veya dijital verilerin işlenmesi

Aşağıdaki bloklar Digital data acquisition systems.

• Transducer - Fiziksel büyüklükleri elektrik sinyallerine çevirir.

• Signal conditioner - Sinyalin istenen kısmının yükseltilmesi ve seçilmesi gibi işlevleri yerine getirir.

• Multiplexer- çoklu girişlerden birini çıkışa bağlar. Yani seri dönüştürücüye paralel olarak hareket eder.

• Analog to Digital Converter - Analog girişi eşdeğer dijital çıkışına dönüştürür.

• Display device - Verileri dijital formatta görüntüler.

• Digital Recorder - Verileri dijital formatta kaydetmek için kullanılır.

Veri toplama sistemleri, biyomedikal ve havacılık gibi çeşitli uygulamalarda kullanılmaktadır. Bu nedenle, ihtiyaca göre analog veri toplama sistemlerini veya dijital veri toplama sistemlerini seçebiliriz.