Giao tiếp tương tự - Bộ điều chế FM

Trong chương này, chúng ta hãy thảo luận về các bộ điều chế tạo ra sóng NBFM và WBFM. Đầu tiên, chúng ta hãy thảo luận về thế hệ NBFM.

Thế hệ NBFM

Chúng ta biết rằng phương trình chuẩn của sóng FM là

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$

$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) - $

$ A_c \ sin \ left (2 \ pi f_ct \ right) \ sin \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) $

Đối với NBFM,

$$ \ left | 2 \ pi k_f \ int m \ left (t \ right) dt \ right | <<1 $$

Chúng tôi biết rằng $ \ cos \ theta \ khoảng 1 $ và $ \ sin \ theta \ khoảng 1 $ khi $ \ theta $ rất nhỏ.

Bằng cách sử dụng các quan hệ trên, chúng ta sẽ nhận được NBFM equation như

$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) -A_c \ sin \ left (2 \ pi f_ct \ right) 2 \ pi k_f \ int m \ left (t \ đúng) dt $$

Sơ đồ khối của bộ điều chế NBFM được thể hiện trong hình sau.

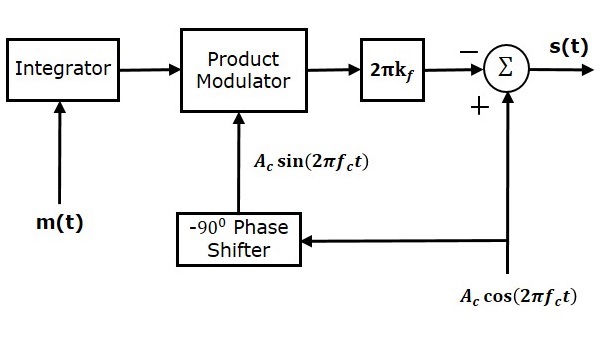
Ở đây, bộ tích hợp được sử dụng để tích hợp tín hiệu điều chế $ m \ left (t \ right) $. Tín hiệu sóng mang $ A_c \ cos \ left (2 \ pi f_ct \ right) $ được dịch chuyển pha bởi $ -90 ^ 0 $ để có được $ A_c \ sin \ left (2 \ pi f_ct \ right) $ với sự trợ giúp của Bộ dịch pha $ -90 ^ 0 $. Bộ điều chế sản phẩm có hai đầu vào $ \ int m \ left (t \ right) dt $ và $ A_c \ sin \ left (2 \ pi f_ct \ right) $. Nó tạo ra một đầu ra, là sản phẩm của hai đầu vào này.

Điều này còn được nhân lên với $ 2 \ pi k_f $ bằng cách đặt một khối $ 2 \ pi k_f $ trong đường dẫn phía trước. Khối mùa hè có hai đầu vào, không là gì ngoài hai số hạng của phương trình NBFM. Các dấu tích cực và tiêu cực được gán cho tín hiệu sóng mang và số hạng khác ở đầu vào của khối mùa hè. Cuối cùng, khối mùa hè tạo ra sóng NBFM.

Thế hệ WBFM

Hai phương pháp sau tạo ra sóng WBFM.

Phương pháp trực tiếp
Phương pháp gián tiếp

Phương pháp trực tiếp

Phương pháp này được gọi là Phương pháp Trực tiếp vì chúng tôi đang tạo ra một sóng FM băng rộng trực tiếp. Trong phương pháp này, Bộ dao động điều khiển bằng điện áp (VCO) được sử dụng để tạo WBFM. VCO tạo ra tín hiệu đầu ra, có tần số tỷ lệ với điện áp tín hiệu đầu vào. Điều này tương tự như định nghĩa của sóng FM. Sơ đồ khối của quá trình tạo ra sóng WBFM được thể hiện trong hình sau.

Ở đây, tín hiệu điều chế $ m \ left (t \ right) $ được áp dụng làm đầu vào của Bộ tạo dao động điều khiển bằng điện áp (VCO). VCO tạo ra một đầu ra, không gì khác ngoài WBFM.

$$ f_i \: \ alpha \: m \ left (t \ right) $$

$$ \ Rightarrow f_i = f_c + k_fm \ left (t \ right) $$

Ở đâu,

$ f_i $ là tần số tức thời của sóng WBFM.

Phương pháp gián tiếp

Phương pháp này được gọi là Phương pháp gián tiếp vì chúng ta đang tạo ra một sóng FM băng rộng một cách gián tiếp. Điều này có nghĩa là, đầu tiên chúng ta sẽ tạo ra sóng NBFM và sau đó với sự trợ giúp của bộ nhân tần số, chúng ta sẽ có được sóng WBFM. Sơ đồ khối tạo ra sóng WBFM được thể hiện trong hình sau.

Sơ đồ khối này chủ yếu chứa hai giai đoạn. Trong giai đoạn đầu, sóng NBFM sẽ được tạo ra bằng bộ điều chế NBFM. Chúng ta đã xem sơ đồ khối của bộ điều chế NBFM ở đầu chương này. Chúng ta biết rằng chỉ số điều chế của sóng NBFM nhỏ hơn một. Do đó, để có được chỉ số điều chế cần thiết (lớn hơn một) của sóng FM, hãy chọn đúng giá trị hệ số nhân tần số.

Frequency multiplierlà một thiết bị phi tuyến tính, tạo ra tín hiệu đầu ra có tần số gấp 'n' lần tần số tín hiệu đầu vào. Trong đó, 'n' là hệ số nhân.

Nếu sóng NBFM có chỉ số điều chế $ \ beta $ nhỏ hơn 1 được áp dụng làm đầu vào của hệ số nhân tần số, thì hệ số nhân tần số tạo ra tín hiệu đầu ra, có chỉ số điều chế là 'n' nhân với $ \ beta $ và tần số cũng là 'n 'lần tần số của sóng WBFM.

Đôi khi, chúng tôi có thể yêu cầu nhiều giai đoạn của bộ nhân tần số và bộ trộn để tăng độ lệch tần số và chỉ số điều chế của sóng FM.