Dòng Fourier và Biến đổi

Trong hướng dẫn cuối cùng về Phân tích miền tần số, chúng ta đã thảo luận rằng chuỗi Fourier và phép biến đổi Fourier được sử dụng để chuyển đổi tín hiệu sang miền tần số.

Fourier

Fourier là một nhà toán học năm 1822. Ông đưa ra chuỗi Fourier và phép biến đổi Fourier để chuyển tín hiệu thành miền tần số.

Loạt Fourier

Chuỗi Fourier chỉ đơn giản nói rằng, các tín hiệu tuần hoàn có thể được biểu diễn thành tổng các sin và cosin khi được nhân với một trọng số nhất định. Nó cũng nói thêm rằng các tín hiệu tuần hoàn có thể được chia thành các tín hiệu khác với các đặc tính sau.

Các tín hiệu là sin và cosine
Các tín hiệu là sóng hài của nhau

Nó có thể được xem bằng hình ảnh là

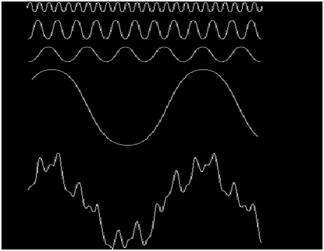
Trong tín hiệu trên, tín hiệu cuối cùng thực sự là tổng của tất cả các tín hiệu trên. Đây là ý tưởng của Fourier.

Nó được tính như thế nào

Vì như chúng ta đã thấy trong miền tần số, để xử lý một hình ảnh trong miền tần số, trước tiên chúng ta cần chuyển đổi nó bằng cách sử dụng thành miền tần số và chúng ta phải lấy nghịch đảo của đầu ra để chuyển nó trở lại miền không gian. Đó là lý do tại sao cả chuỗi Fourier và biến đổi Fourier đều có hai công thức. Một để chuyển đổi và một chuyển đổi nó trở lại miền không gian.

loạt Fourier

Chuỗi Fourier có thể được ký hiệu bằng công thức này.

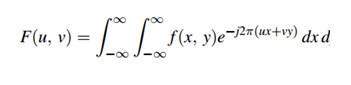
Có thể tính toán nghịch đảo bằng công thức này.

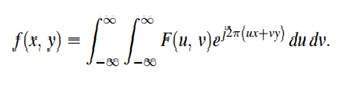
Biến đổi Fourier

Phép biến đổi Fourier đơn giản chỉ ra rằng các tín hiệu không tuần hoàn có diện tích dưới đường cong là hữu hạn cũng có thể được biểu diễn thành tích phân của sin và cosin sau khi được nhân với một trọng số nhất định.

Biến đổi Fourier có nhiều ứng dụng rộng rãi bao gồm nén hình ảnh (ví dụ nén JPEG), lọc và phân tích hình ảnh.

Sự khác biệt giữa chuỗi Fourier và phép biến đổi

Mặc dù cả chuỗi Fourier và biến đổi Fourier đều do Fourier đưa ra, nhưng sự khác biệt giữa chúng là chuỗi Fourier được áp dụng cho các tín hiệu tuần hoàn và phép biến đổi Fourier được áp dụng cho các tín hiệu không tuần hoàn

Cái nào được áp dụng trên hình ảnh

Bây giờ câu hỏi là cái nào được áp dụng trên các hình ảnh, chuỗi Fourier hay phép biến đổi Fourier. Vâng, câu trả lời cho câu hỏi này nằm trong thực tế là những hình ảnh là gì. Hình ảnh không theo chu kỳ. Và vì ảnh không tuần hoàn, nên phép biến đổi Fourier được sử dụng để chuyển chúng thành miền tần số.

Biến đổi fourier rời rạc

Vì chúng tôi đang xử lý hình ảnh và trên thực tế là hình ảnh kỹ thuật số, vì vậy đối với hình ảnh kỹ thuật số, chúng tôi sẽ nghiên cứu chuyển đổi fourier rời rạc

Xét số hạng Fourier trên của một hình sin. Nó bao gồm ba điều.

Tần số không gian
Magnitude
Phase

Tần số không gian liên quan trực tiếp đến độ sáng của hình ảnh. Độ lớn của hình sin liên quan trực tiếp với độ tương phản. Độ tương phản là sự khác biệt giữa cường độ pixel tối đa và tối thiểu. Pha chứa thông tin về màu sắc.

Công thức cho phép biến đổi Fourier rời rạc 2 chiều được đưa ra dưới đây.

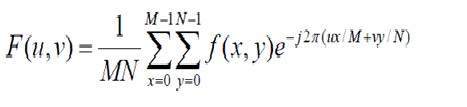
Biến đổi Fourier rời rạc thực sự là biến đổi Fourier được lấy mẫu, vì vậy nó chứa một số mẫu biểu thị một hình ảnh. Trong công thức trên, f (x, y) biểu thị ảnh và F (u, v) biểu thị biến đổi Fourier rời rạc. Công thức cho phép biến đổi Fourier rời rạc nghịch đảo 2 chiều được đưa ra dưới đây.

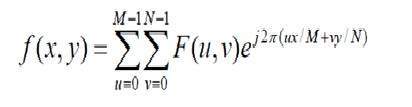
Phép biến đổi Fourier rời rạc nghịch đảo chuyển phép biến đổi Fourier trở lại hình ảnh

Xem xét tín hiệu này

Bây giờ chúng ta sẽ thấy một hình ảnh, chúng ta sẽ tính toán phổ cường độ FFT và sau đó là phổ cường độ FFT dịch chuyển và sau đó chúng ta sẽ lấy Log của quang phổ được dịch chuyển đó.