Chuyển đổi mức xám

Chúng tôi đã thảo luận về một số phép biến đổi cơ bản trong hướng dẫn của chúng tôi về Phép biến đổi cơ bản. Trong hướng dẫn này, chúng ta sẽ xem xét một số phép biến đổi mức xám cơ bản.

Nâng cao hình ảnh

Nâng cao hình ảnh cung cấp độ tương phản tốt hơn và hình ảnh chi tiết hơn so với hình ảnh không nâng cao. Nâng cao hình ảnh có rất nhiều ứng dụng. Nó được sử dụng để nâng cao hình ảnh y tế, hình ảnh thu được trong viễn thám, hình ảnh từ vệ tinh, v.v.

Hàm biến đổi đã được đưa ra bên dưới

s = T (r)

trong đó r là pixel của hình ảnh đầu vào và s là pixel của hình ảnh đầu ra. T là một hàm biến đổi ánh xạ từng giá trị của r thành từng giá trị của s. Nâng cao hình ảnh có thể được thực hiện thông qua các phép biến đổi mức xám được thảo luận bên dưới.

Chuyển đổi mức xám

Có ba chuyển đổi mức xám cơ bản.

Linear
Logarithmic
Sức mạnh của pháp luật

Biểu đồ tổng thể của những chuyển đổi này đã được hiển thị bên dưới.

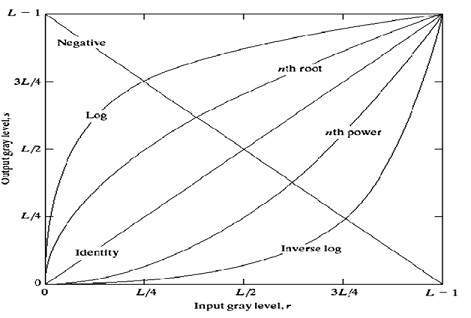
Chuyển đổi tuyến tính

Đầu tiên chúng ta sẽ xem xét phép biến đổi tuyến tính. Phép biến đổi tuyến tính bao gồm phép đồng dạng đơn giản và phép biến đổi phủ định. Chuyển đổi danh tính đã được thảo luận trong hướng dẫn của chúng tôi về chuyển đổi hình ảnh, nhưng mô tả ngắn gọn về chuyển đổi này đã được đưa ra ở đây.

Sự chuyển đổi nhận dạng được thể hiện bằng một đường thẳng. Trong quá trình chuyển đổi này, mỗi giá trị của hình ảnh đầu vào được ánh xạ trực tiếp với mỗi giá trị khác của hình ảnh đầu ra. Điều đó dẫn đến hình ảnh đầu vào và hình ảnh đầu ra giống nhau. Và do đó được gọi là chuyển đổi danh tính. Nó đã được hiển thị bên dưới:

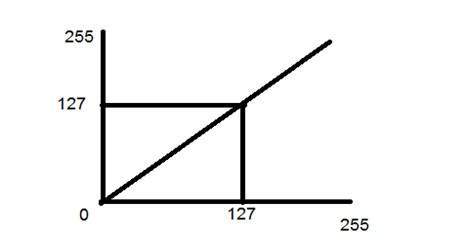
Chuyển đổi tiêu cực

Phép biến đổi tuyến tính thứ hai là phép biến đổi âm, là phép biến đổi đảo ngược của phép biến đổi nhận dạng. Trong phép biến đổi âm, mỗi giá trị của hình ảnh đầu vào được trừ đi từ L-1 và được ánh xạ vào hình ảnh đầu ra.

Kết quả là phần nào như thế này.

Hình ảnh đầu vào

Hình ảnh đầu ra

Trong trường hợp này, quá trình chuyển đổi sau đã được thực hiện.

s = (L - 1) - r

vì hình ảnh đầu vào của Einstein là hình ảnh 8 bpp, vì vậy số mức trong hình ảnh này là 256. Đặt 256 vào phương trình, chúng ta nhận được

s = 255 - r

Vì vậy, mỗi giá trị được trừ đi 255 và hình ảnh kết quả đã được hiển thị ở trên. Vì vậy, những gì sẽ xảy ra là, các điểm ảnh sáng hơn trở nên tối và hình ảnh tối hơn trở thành ánh sáng. Và nó dẫn đến hình ảnh âm tính.

Nó đã được hiển thị trong biểu đồ bên dưới.

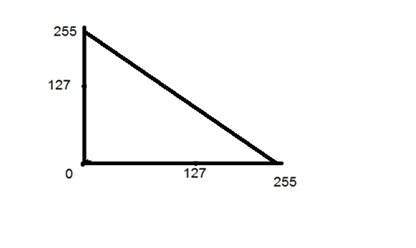
Phép biến đổi lôgarit

Phép biến đổi lôgarit còn có hai loại phép biến đổi. Phép biến đổi log và phép biến đổi log ngược.

Chuyển đổi nhật ký

Các phép biến đổi nhật ký có thể được xác định bằng công thức này

s = c log (r + 1).

Trong đó s và r là giá trị pixel của đầu ra và hình ảnh đầu vào và c là một hằng số. Giá trị 1 được thêm vào mỗi giá trị pixel của hình ảnh đầu vào bởi vì nếu có cường độ pixel bằng 0 trong hình ảnh thì log (0) bằng vô cực. Vì vậy, 1 được thêm vào, để làm cho giá trị nhỏ nhất ít nhất là 1.

Trong quá trình chuyển đổi nhật ký, các pixel tối trong hình ảnh được mở rộng so với các giá trị pixel cao hơn. Các giá trị pixel cao hơn được nén trong phép biến đổi nhật ký. Điều này dẫn đến việc nâng cao hình ảnh sau đây.

Giá trị của c trong biến đổi nhật ký điều chỉnh loại cải tiến bạn đang tìm kiếm.

Hình ảnh đầu vào

Nhật ký Tranform Image

Phép biến đổi log nghịch đảo ngược lại với phép biến đổi log.

Quyền lực - Các phép biến đổi luật

Có hai phép biến đổi nữa là phép biến đổi luật lũy thừa, bao gồm phép biến đổi lũy thừa thứ n và phép biến đổi gốc thứ n. Các phép biến đổi này có thể được cho bởi biểu thức:

s = cr ^ γ

Ký hiệu γ này được gọi là gamma, do đó biến đổi này còn được gọi là biến đổi gamma.

Sự thay đổi trong giá trị của γ sẽ thay đổi mức độ nâng cao của hình ảnh. Các thiết bị / màn hình hiển thị khác nhau có hiệu chỉnh gamma riêng, đó là lý do tại sao chúng hiển thị hình ảnh ở cường độ khác nhau.

Loại biến đổi này được sử dụng để nâng cao hình ảnh cho các loại thiết bị hiển thị khác nhau. Gamma của các thiết bị hiển thị khác nhau là khác nhau. Ví dụ Gamma của CRT nằm trong khoảng từ 1,8 đến 2,5, có nghĩa là hình ảnh hiển thị trên CRT là tối.