Kỹ thuật hồi quy
Hồi quy là một kỹ thuật thống kê giúp xác định mối quan hệ giữa các biến số kinh tế có liên quan với nhau. Bước đầu tiên liên quan đến việc ước lượng hệ số của biến độc lập và sau đó đo độ tin cậy của hệ số ước lượng. Điều này đòi hỏi phải xây dựng một giả thuyết, và dựa trên giả thuyết, chúng ta có thể tạo ra một hàm.
Nếu một nhà quản lý muốn xác định mối quan hệ giữa chi phí quảng cáo của công ty và doanh thu bán hàng của công ty, anh ta sẽ trải qua bài kiểm tra giả thuyết. Giả sử rằng chi phí quảng cáo cao hơn dẫn đến doanh thu cao hơn cho một công ty. Người quản lý thu thập dữ liệu về chi tiêu quảng cáo và doanh thu bán hàng trong một khoảng thời gian cụ thể. Giả thuyết này có thể được chuyển thành hàm toán học, nơi nó dẫn đến -
Y = A + Bx
Ở đâu Y là bán hàng, x là chi phí quảng cáo, A và B là không đổi.
Sau khi chuyển giả thuyết thành hàm, cơ sở cho việc này là tìm mối quan hệ giữa các biến phụ thuộc và độc lập. Giá trị của biến phụ thuộc có tầm quan trọng nhất đối với các nhà nghiên cứu và phụ thuộc vào giá trị của các biến khác. Biến độc lập được sử dụng để giải thích sự thay đổi của biến phụ thuộc. Nó có thể được phân thành hai loại -
Simple regression - Một biến độc lập
Multiple regression - Một số biến độc lập
Hồi quy đơn giản
Sau đây là các bước để xây dựng phân tích hồi quy -
- Chỉ định mô hình hồi quy
- Lấy dữ liệu về các biến
- Ước tính các mối quan hệ định lượng
- Kiểm tra ý nghĩa thống kê của các kết quả
- Sử dụng kết quả trong việc ra quyết định
Công thức cho hồi quy đơn giản là -
Y = a + bX + u
Y= biến phụ thuộc
X= biến độc lập
a= đánh chặn
b= độ dốc
u= yếu tố ngẫu nhiên
Dữ liệu mặt cắt cung cấp thông tin về một nhóm thực thể tại một thời điểm nhất định, trong khi dữ liệu chuỗi thời gian cung cấp thông tin về một thực thể theo thời gian. Khi chúng ta ước lượng phương trình hồi quy, nó liên quan đến quá trình tìm ra mối quan hệ tuyến tính tốt nhất giữa các biến phụ thuộc và các biến độc lập.
Phương pháp Bình phương Ít nhất Thông thường (OLS)
Phương pháp bình phương nhỏ nhất thông thường được thiết kế để điều chỉnh một đường thẳng đi qua một điểm phân tán, sao cho tổng bình phương độ lệch của các điểm so với đường thẳng được giảm thiểu. Đó là một phương pháp thống kê. Thông thường các gói Phần mềm thực hiện ước lượng OLS.
Y = a + bX
Đồng hiệu quả của xác định (R 2 )
Hiệu quả xác định là một thước đo cho biết tỷ lệ phần trăm của sự thay đổi trong biến phụ thuộc là do sự thay đổi của các biến độc lập. R 2 là thước đo độ tốt của mô hình phù hợp. Sau đây là các phương pháp -
Tổng bình phương (TSS)
Tổng bình phương độ lệch của các giá trị mẫu của Y so với giá trị trung bình của Y.
TSS = SUM ( Yi − Y)2
Yi = biến phụ thuộc
Y = giá trị trung bình của các biến phụ thuộc
i = số quan sát
Hồi quy Tổng bình phương (RSS)
Tổng bình phương độ lệch của các giá trị ước tính của Y so với giá trị trung bình của Y.
RSS = SUM ( Ỷi − uY)2
Ỷi = giá trị ước tính của Y
Y = giá trị trung bình của các biến phụ thuộc
i = số biến thể
Tổng sai số của bình phương (ESS)
Tổng các độ lệch bình phương của các giá trị mẫu của Y so với các giá trị ước tính của Y.
ESS = SUM ( Yi − Ỷi)2
Ỷi = giá trị ước tính của Y
Yi = biến phụ thuộc
i = số quan sát
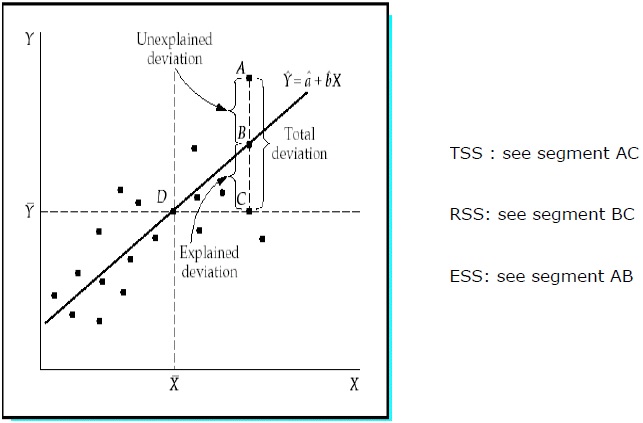
R 2 đo lường tỷ lệ của tổng độ lệch của Y so với giá trị trung bình của nó, được giải thích bằng mô hình hồi quy. R 2 càng gần với sự thống nhất, sức mạnh giải thích của phương trình hồi quy càng lớn. R 2 gần bằng 0 chỉ ra rằng phương trình hồi quy sẽ có rất ít sức mạnh giải thích.
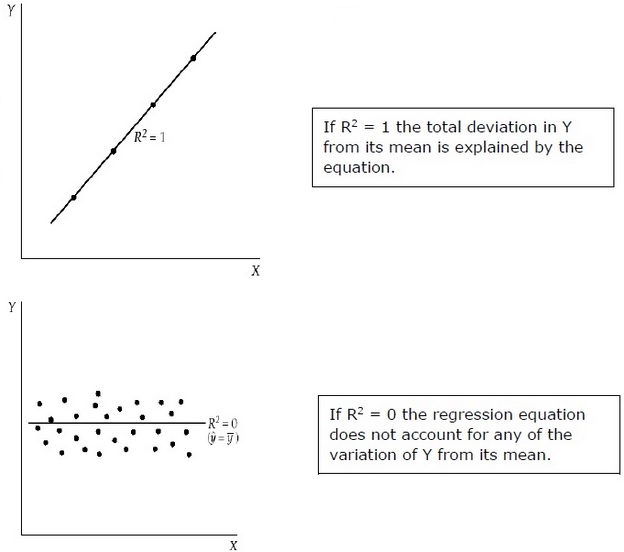
Để đánh giá các hệ số hồi quy, một mẫu từ tổng thể được sử dụng thay vì toàn bộ tổng thể. Điều quan trọng là phải đưa ra các giả định về dân số dựa trên mẫu và đưa ra đánh giá về mức độ tốt của các giả định này.
Đánh giá hệ số hồi quy
Mỗi mẫu từ tổng thể tạo ra điểm chặn của riêng nó. Để tính toán sự khác biệt thống kê có thể được sử dụng các phương pháp sau:
Two tailed test −
Giả thuyết Null: H 0 : b = 0
Giả thuyết thay thế: H a : b ≠ 0
One tailed test −
Giả thuyết Null: H 0 : b> 0 (hoặc b <0)
Giả thuyết thay thế: H a : b <0 (hoặc b> 0)
Statistic Test −
b = hệ số ước tính
E (b) = b = 0 (Giả thuyết vô hiệu)
SE b = Sai số tiêu chuẩn của hệ số
.Giá trị của tphụ thuộc vào mức độ tự do, một hoặc hai lần thử nghiệm không đạt và mức ý nghĩa. Để xác định giá trị tới hạn củat, bảng t có thể được sử dụng. Sau đó là so sánh giá trị t với giá trị tới hạn. Người ta cần bác bỏ giả thuyết vô hiệu nếu giá trị tuyệt đối của kiểm định thống kê lớn hơn hoặc bằng giá trị t tới hạn. Không bác bỏ giả thuyết vô hiệu, tôi giá trị tuyệt đối của kiểm định thống kê nhỏ hơn giá trị t tới hạn.
Phân tích hồi quy đa biến
Không giống như hồi quy đơn giản trong phân tích hồi quy bội, các hệ số chỉ ra sự thay đổi của các biến phụ thuộc với giả định giá trị của các biến khác là không đổi.
Kiểm định ý nghĩa thống kê được gọi là F-test. Kiểm định F rất hữu ích vì nó đo lường ý nghĩa thống kê của toàn bộ phương trình hồi quy thay vì chỉ cho một cá nhân. Ở đây Trong giả thuyết rỗng, không có mối quan hệ giữa biến phụ thuộc và các biến độc lập của tổng thể.
Công thức là - H 0 : b1 = b2 = b3 =…. = bk = 0
Không có mối quan hệ nào tồn tại giữa biến phụ thuộc và k các biến độc lập đối với dân số.
F-test static −
$$ F \: = \: \ frac {\ left (\ frac {R ^ 2} {K} \ right)} {\ frac {(1-R ^ 2)} {(nk-1)}} $$
Giá trị quan trọng của Fphụ thuộc vào tử số và mẫu số bậc tự do và mức ý nghĩa. Bảng F có thể được sử dụng để xác định giá trị F tới hạn. So với giá trị F với giá trị tới hạn (F *) -
Nếu F> F *, chúng ta cần bác bỏ giả thuyết rỗng.
Nếu F <F *, không bác bỏ giả thuyết rỗng vì không có mối quan hệ đáng kể nào giữa biến phụ thuộc và tất cả các biến độc lập.