MATLAB - Giải tích

MATLAB cung cấp nhiều cách khác nhau để giải các bài toán về phép tính vi phân và tích phân, giải phương trình vi phân cấp độ bất kỳ và tính các giới hạn. Hơn hết, bạn có thể dễ dàng vẽ đồ thị của các hàm số phức tạp và kiểm tra cực đại, cực tiểu và các điểm văn phòng phẩm khác trên đồ thị bằng cách giải hàm gốc, cũng như đạo hàm của nó.

Chương này sẽ giải quyết các vấn đề về giải tích. Trong chương này, chúng ta sẽ thảo luận về các khái niệm tiền tích, tức là tính toán giới hạn của hàm số và xác minh các tính chất của giới hạn.

Trong chương tiếp theo Vi phân , chúng ta sẽ tính đạo hàm của một biểu thức và tìm cực đại và cực tiểu cục bộ trên đồ thị. Chúng ta cũng sẽ thảo luận về việc giải các phương trình vi phân.

Cuối cùng, trong chương Tích phân , chúng ta sẽ thảo luận về phép tính tích phân.

Tính toán giới hạn

MATLAB cung cấp limithàm tính toán giới hạn. Ở dạng cơ bản nhất,limit hàm nhận biểu thức làm đối số và tìm giới hạn của biểu thức khi biến độc lập về 0.

Ví dụ, chúng ta hãy tính giới hạn của một hàm f (x) = (x ³ + 5) / (x ⁴ + 7), vì x có xu hướng bằng không.

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   5/7

Hàm giới hạn thuộc lĩnh vực tính toán tượng trưng; bạn cần sử dụngsymshàm cho MATLAB biết bạn đang sử dụng biến tượng trưng nào. Bạn cũng có thể tính toán giới hạn của một hàm, vì biến có xu hướng là một số nào đó khác 0. Để tính lim _{x-> a} (f (x)), ta sử dụng lệnh giới hạn với các đối số. Đầu tiên là biểu thức và thứ hai là số, mà x tiếp cận, đây là a .

Ví dụ, chúng ta hãy tính giới hạn của một hàm f (x) = (x-3) / (x-1), vì x có xu hướng bằng 1.

limit((x - 3)/(x-1),1)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   NaN

Hãy lấy một ví dụ khác,

limit(x^2 + 5, 3)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   14

Tính toán giới hạn bằng Octave

Sau đây là phiên bản Octave của ví dụ trên bằng cách sử dụng symbolic gói, cố gắng thực thi và so sánh kết quả -

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   0.7142857142857142857

Xác minh các thuộc tính cơ bản của giới hạn

Định lý giới hạn đại số cung cấp một số tính chất cơ bản của giới hạn. Những điều này như sau:

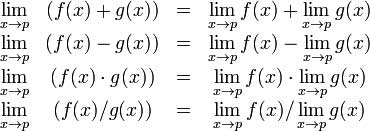
Chúng ta hãy xem xét hai chức năng -

f (x) = (3x + 5) / (x - 3)
g (x) = x ² + 1.

Chúng ta hãy tính giới hạn của các hàm khi x có xu hướng bằng 5 của cả hai hàm và xác minh các tính chất cơ bản của giới hạn bằng cách sử dụng hai hàm này và MATLAB.

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

Khi bạn chạy tệp, nó sẽ hiển thị -

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

Xác minh các thuộc tính cơ bản của giới hạn bằng Octave

Sau đây là phiên bản Octave của ví dụ trên bằng cách sử dụng symbolic gói, cố gắng thực thi và so sánh kết quả -

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave sẽ thực hiện câu lệnh trên và trả về kết quả sau:

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

Giới hạn bên trái và bên phải

Khi một hàm có sự gián đoạn đối với một giá trị cụ thể nào đó của biến, giới hạn không tồn tại tại điểm đó. Nói cách khác, giới hạn của hàm f (x) không liên tục tại x = a, khi giá trị của giới hạn, khi x tiếp cận x từ phía bên trái, không bằng giá trị của giới hạn khi x tiếp cận từ phía bên phải.

Điều này dẫn đến khái niệm về giới hạn thuận tay trái và tay phải. Giới hạn thuận tay trái được định nghĩa là giới hạn khi x -> a, từ bên trái, tức là x tiến tới a, với các giá trị của x <a. Giới hạn thuận tay phải được định nghĩa là giới hạn khi x -> a, từ bên phải, tức là x tiến tới a, với các giá trị của x> a. Khi giới hạn thuận tay trái và giới hạn thuận tay phải không bằng nhau, giới hạn đó không tồn tại.

Chúng ta hãy xem xét một chức năng -

f(x) = (x - 3)/|x - 3|

Ta sẽ chứng tỏ rằng lim _{x-> 3} f (x) không tồn tại. MATLAB giúp chúng tôi xác định thực tế này theo hai cách -

Bằng cách vẽ đồ thị của hàm số và thể hiện tính gián đoạn.
Bằng cách tính toán các giới hạn và cho thấy rằng cả hai đều khác nhau.

Giới hạn tay trái và tay phải được tính bằng cách chuyển các chuỗi ký tự 'left' và 'right' vào lệnh giới hạn làm đối số cuối cùng.

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

Khi bạn chạy tệp, MATLAB vẽ sơ đồ sau

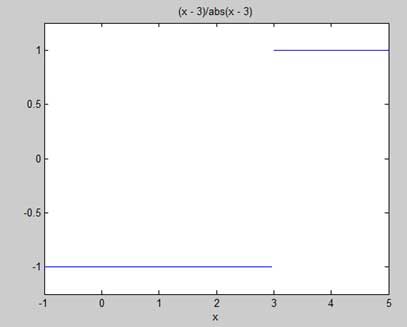
Sau khi đầu ra sau đây được hiển thị -

l =
   -1
  
r =
   1