MATLAB - Hướng dẫn nhanh

MATLAB (phòng thí nghiệm ma trận) là một ngôn ngữ lập trình bậc cao thế hệ thứ tư và môi trường tương tác để tính toán, hiển thị và lập trình số.

MATLAB được phát triển bởi MathWorks.

Nó cho phép các thao tác ma trận; biểu đồ của các chức năng và dữ liệu; thực hiện các thuật toán; tạo giao diện người dùng; giao tiếp với các chương trình được viết bằng các ngôn ngữ khác, bao gồm C, C ++, Java và FORTRAN; phân tích dữ liệu; phát triển các thuật toán; và tạo ra các mô hình và ứng dụng.

Nó có nhiều lệnh và hàm toán học được tích hợp sẵn giúp bạn tính toán toán học, tạo các biểu đồ và thực hiện các phương pháp số.

Sức mạnh Toán học Tính toán của MATLAB

MATLAB được sử dụng trong mọi khía cạnh của toán học tính toán. Sau đây là một số phép tính toán học thường được sử dụng trong đó nó được sử dụng phổ biến nhất:

• Xử lý ma trận và mảng
• Vẽ và đồ họa 2-D và 3-D
• Đại số tuyến tính
• Phương trình đại số
• Hàm phi tuyến tính
• Statistics
• Phân tích dữ liệu
• Giải tích và phương trình vi phân
• Tính toán số
• Integration
• Transforms
• Đường cong phù hợp
• Nhiều chức năng đặc biệt khác

Các tính năng của MATLAB

Sau đây là các tính năng cơ bản của MATLAB:

• Nó là một ngôn ngữ cấp cao để tính toán số, trực quan hóa và phát triển ứng dụng.

• Nó cũng cung cấp một môi trường tương tác để khám phá lặp đi lặp lại, thiết kế và giải quyết vấn đề.

• Nó cung cấp thư viện rộng lớn các hàm toán học cho đại số tuyến tính, thống kê, phân tích Fourier, lọc, tối ưu hóa, tích phân số và giải phương trình vi phân thông thường.

• Nó cung cấp đồ họa tích hợp để trực quan hóa dữ liệu và các công cụ để tạo các ô tùy chỉnh.

• Giao diện lập trình của MATLAB cung cấp các công cụ phát triển để cải thiện khả năng bảo trì chất lượng mã và tối đa hóa hiệu suất.

• Nó cung cấp các công cụ để xây dựng ứng dụng với giao diện đồ họa tùy chỉnh.

• Nó cung cấp các chức năng để tích hợp các thuật toán dựa trên MATLAB với các ứng dụng và ngôn ngữ bên ngoài như C, Java, .NET và Microsoft Excel.

Công dụng của MATLAB

MATLAB được sử dụng rộng rãi như một công cụ tính toán trong khoa học và kỹ thuật bao gồm các lĩnh vực vật lý, hóa học, toán học và tất cả các luồng kỹ thuật. Nó được sử dụng trong một loạt các ứng dụng bao gồm:

• Xử lý tín hiệu và truyền thông
• Xử lý hình ảnh và video
• Hệ thống điều khiển
• Kiểm tra và Đo lường
• Tài chính tính toán
• Sinh hoc tinh toan

Thiết lập môi trường cục bộ

Việc thiết lập môi trường MATLAB chỉ là một vài cú nhấp chuột. Trình cài đặt có thể được tải xuống từ đây .

MathWorks cung cấp sản phẩm được cấp phép, phiên bản dùng thử và cả phiên bản dành cho sinh viên. Bạn cần đăng nhập vào trang web và đợi một chút để họ chấp thuận.

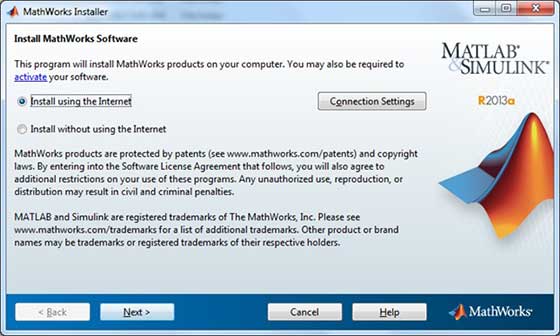
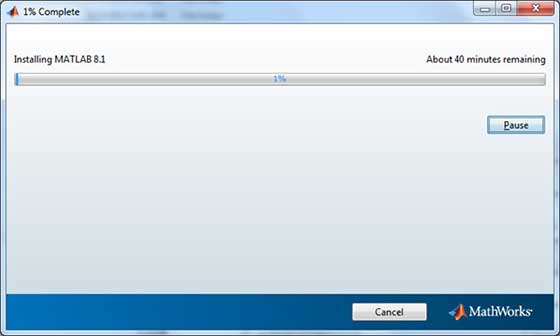
Sau khi tải xuống trình cài đặt, phần mềm có thể được cài đặt thông qua một vài cú nhấp chuột.

Hiểu môi trường MATLAB

IDE phát triển MATLAB có thể được khởi chạy từ biểu tượng được tạo trên màn hình nền. Cửa sổ làm việc chính trong MATLAB được gọi là màn hình nền. Khi MATLAB được khởi động, màn hình sẽ xuất hiện trong bố cục mặc định của nó -

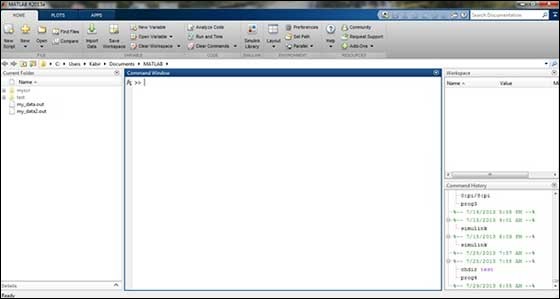
Máy tính để bàn có các bảng sau:

• Current Folder - Bảng điều khiển này cho phép bạn truy cập các thư mục và tệp của dự án.



• Command Window- Đây là khu vực chính có thể nhập các lệnh tại dòng lệnh. Nó được chỉ ra bởi dấu nhắc lệnh (>>).



• Workspace - Không gian làm việc hiển thị tất cả các biến được tạo và / hoặc nhập từ tệp.



• Command History - Bảng này hiển thị hoặc trả về các lệnh được nhập tại dòng lệnh.

Thiết lập GNU Octave

Nếu bạn muốn sử dụng Octave trên máy tính của mình (Linux, BSD, OS X hoặc Windows), vui lòng tải xuống phiên bản mới nhất từ Tải xuống GNU Octave . Bạn có thể kiểm tra hướng dẫn cài đặt cho máy của mình.

Môi trường MATLAB hoạt động giống như một máy tính siêu phức tạp. Bạn có thể nhập lệnh tại dấu nhắc lệnh >>.

MATLAB là một môi trường thông dịch. Nói cách khác, bạn đưa ra một lệnh và MATLAB thực thi nó ngay lập tức.

Thực hành

Nhập một biểu thức hợp lệ, ví dụ:

5 + 5

Và nhấn ENTER

Khi bạn nhấp vào nút Execute hoặc gõ Ctrl + E, MATLAB sẽ thực thi nó ngay lập tức và kết quả trả về là:

ans = 10

Hãy để chúng tôi lấy thêm một vài ví dụ -

3 ^ 2	       % 3 raised to the power of 2

Khi bạn nhấp vào nút Execute hoặc gõ Ctrl + E, MATLAB sẽ thực thi nó ngay lập tức và kết quả trả về là:

ans = 9

Một vi dụ khac,

sin(pi /2)	  % sine of angle 90o

Khi bạn nhấp vào nút Execute hoặc gõ Ctrl + E, MATLAB sẽ thực thi nó ngay lập tức và kết quả trả về là:

ans = 1

Một vi dụ khac,

7/0		      % Divide by zero

Khi bạn nhấp vào nút Execute hoặc gõ Ctrl + E, MATLAB sẽ thực thi nó ngay lập tức và kết quả trả về là:

ans = Inf
warning: division by zero

Một vi dụ khac,

732 * 20.3

Khi bạn nhấp vào nút Execute hoặc gõ Ctrl + E, MATLAB sẽ thực thi nó ngay lập tức và kết quả trả về là:

ans =  1.4860e+04

MATLAB cung cấp một số biểu thức đặc biệt cho một số ký hiệu toán học, như pi cho π, Inf cho ∞, i (và j) cho √-1, v.v. Nan là viết tắt của 'not a number'.

Sử dụng Dấu chấm phẩy (;) trong MATLAB

Dấu chấm phẩy (;) cho biết kết thúc câu lệnh. Tuy nhiên, nếu bạn muốn ngăn chặn và ẩn đầu ra MATLAB cho một biểu thức, hãy thêm dấu chấm phẩy sau biểu thức.

Ví dụ,

x = 3;
y = x + 5

Khi bạn nhấp vào nút Execute hoặc gõ Ctrl + E, MATLAB sẽ thực thi nó ngay lập tức và kết quả trả về là:

y =  8

Thêm nhận xét

Biểu tượng phần trăm (%) được sử dụng để chỉ dòng chú thích. Ví dụ,

x = 9	     % assign the value 9 to x

Bạn cũng có thể viết một khối nhận xét bằng cách sử dụng các toán tử nhận xét khối% {và%}.

Trình chỉnh sửa MATLAB bao gồm các công cụ và các mục menu ngữ cảnh để giúp bạn thêm, xóa hoặc thay đổi định dạng của nhận xét.

Các toán tử thường được sử dụng và các ký tự đặc biệt

MATLAB hỗ trợ các toán tử và các ký tự đặc biệt thường được sử dụng sau:

Nhà điều hành	Mục đích
+	Thêm; toán tử cộng.
-	Dấu trừ; toán tử phép trừ.
*	Toán tử vô hướng và nhân ma trận.
.*	Toán tử nhân mảng.
^	Toán tử lũy thừa vô hướng và ma trận.
.^	Toán tử lũy thừa mảng.
\	Toán tử chia trái.
/	Toán tử chia phải.
.\	Toán tử chia trái mảng.
./	Toán tử chia phải mảng.
:	Đại tràng; tạo các phần tử cách đều nhau và đại diện cho toàn bộ hàng hoặc cột.
( )	Dấu ngoặc đơn; bao gồm các đối số hàm và chỉ số mảng; ghi đè mức độ ưu tiên.
[ ]	Chân đế; các phần tử mảng bao vây.
.	Dấu thập phân.
…	Dấu chấm lửng; toán tử tiếp tục dòng
,	Dấu phẩy; tách các câu lệnh và các phần tử trong một hàng
;	Dấu chấm phẩy; tách các cột và ngăn hiển thị.
%	Ký hiệu phần trăm; chỉ định một nhận xét và chỉ định định dạng.
_	Dấu ngoặc kép và toán tử chuyển vị.
._	Toán tử chuyển vị không liên hợp.
=	Toán tử gán.

Các biến và hằng số đặc biệt

MATLAB hỗ trợ các biến và hằng số đặc biệt sau:

Tên	Ý nghĩa
ans	Câu trả lời gần đây nhất.
eps	Độ chính xác của độ chính xác dấu phẩy động.
i,j	Đơn vị ảo √-1.
Inf	Vô cực.
NaN	Kết quả số không xác định (không phải số).
pi	Số π

Đặt tên biến

Tên biến bao gồm một chữ cái theo sau bởi bất kỳ số chữ cái, chữ số hoặc dấu gạch dưới nào.

MATLAB là case-sensitive.

Tên biến có thể có độ dài bất kỳ, tuy nhiên, MATLAB chỉ sử dụng N ký tự đầu tiên, trong đó N được cung cấp bởi hàm namelengthmax.

Lưu công việc của bạn

Các save được sử dụng để lưu tất cả các biến trong không gian làm việc, dưới dạng tệp có phần mở rộng .mat, trong thư mục hiện tại.

Ví dụ,

save myfile

Bạn có thể tải lại tệp bất kỳ lúc nào sau đó bằng cách sử dụng load chỉ huy.

load myfile

Trong môi trường MATLAB, mọi biến là một mảng hoặc ma trận.

Bạn có thể gán các biến một cách đơn giản. Ví dụ,

x = 3	       % defining x and initializing it with a value

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

x = 3

Nó tạo ra một ma trận 1-1 có tên là x và lưu trữ giá trị 3 trong phần tử của nó. Hãy để chúng tôi kiểm tra một ví dụ khác,

x = sqrt(16) 	% defining x and initializing it with an expression

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

x = 4

Xin lưu ý rằng -

• Sau khi một biến được nhập vào hệ thống, bạn có thể tham khảo nó sau.

• Các biến phải có giá trị trước khi chúng được sử dụng.

• Khi một biểu thức trả về một kết quả không được gán cho bất kỳ biến nào, hệ thống sẽ gán nó cho một biến có tên ans, biến này có thể được sử dụng sau này.

Ví dụ,

sqrt(78)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =  8.8318

Bạn có thể sử dụng biến này ans -

sqrt(78);
9876/ans

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =  1118.2

Hãy xem một ví dụ khác -

x = 7 * 8;
y = x * 7.89

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

y =  441.84

Nhiều bài tập

Bạn có thể có nhiều bài tập trên cùng một dòng. Ví dụ,

a = 2; b = 7; c = a * b

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

c = 14

Tôi đã quên các biến!

Các who lệnh hiển thị tất cả các tên biến bạn đã sử dụng.

who

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

Your variables are:
a    ans  b    c

Các whos lệnh hiển thị thêm một chút về các biến -

• Các biến hiện có trong bộ nhớ
• Loại của mỗi biến
• Bộ nhớ được phân bổ cho mỗi biến
• Cho dù chúng có phải là các biến phức tạp hay không

whos

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

Attr Name        Size        Bytes      Class
==== ====        ====        ====       ===== 
   a             1x1           8        double
   ans           1x70         757        cell
   b             1x1           8        double
   c             1x1           8        double

Total is 73 elements using 781 bytes

Các clear lệnh xóa tất cả (hoặc các) biến được chỉ định khỏi bộ nhớ.

clear x     % it will delete x, won't display anything
clear       % it will delete all variables in the workspace
            %  peacefully and unobtrusively

Bài tập dài

Bài tập dài có thể được mở rộng sang một dòng khác bằng cách sử dụng dấu chấm lửng (...). Ví dụ,

initial_velocity = 0;
acceleration = 9.8;
time = 20;
final_velocity = initial_velocity + acceleration * time

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

final_velocity = 196

Lệnh định dạng

Theo mặc định, MATLAB hiển thị các số có bốn giá trị vị trí thập phân. Điều này được gọi làshort format.

Tuy nhiên, nếu bạn muốn chính xác hơn, bạn cần sử dụng format chỉ huy.

Các format long lệnh hiển thị 16 chữ số sau số thập phân.

Ví dụ -

format long
x = 7 + 10/3 + 5 ^ 1.2

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau

x = 17.2319816406394

Một vi dụ khac,

format short
x = 7 + 10/3 + 5 ^ 1.2

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

x = 17.232

Các format banklệnh làm tròn số đến hai chữ số thập phân. Ví dụ,

format bank
daily_wage = 177.45;
weekly_wage = daily_wage * 6

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

weekly_wage = 1064.70

MATLAB hiển thị các số lớn bằng cách sử dụng ký hiệu hàm mũ.

Các format short e lệnh cho phép hiển thị dưới dạng lũy ​​thừa với bốn chữ số thập phân cộng với số mũ.

Ví dụ,

format short e
4.678 * 4.9

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans = 2.2922e+01

Các format long elệnh cho phép hiển thị dưới dạng lũy ​​thừa với bốn chữ số thập phân cộng với số mũ. Ví dụ,

format long e
x = pi

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

x = 3.141592653589793e+00

Các format ratlệnh cho biểu thức hữu tỉ gần nhất kết quả từ một phép tính. Ví dụ,

format rat
4.678 * 4.9

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans = 34177/1491

Tạo vectơ

Vectơ là một mảng số một chiều. MATLAB cho phép tạo hai loại vectơ:

• Vectơ hàng
• Vectơ cột

Row vectors được tạo bằng cách đặt tập hợp các phần tử trong dấu ngoặc vuông, sử dụng dấu cách hoặc dấu phẩy để phân cách các phần tử.

Ví dụ,

r = [7 8 9 10 11]

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

r =

   7    8    9   10   11

Một vi dụ khac,

r = [7 8 9 10 11];
t = [2, 3, 4, 5, 6];
res = r + t

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

res =

         9         11         13         15         17

Column vectors được tạo bằng cách đặt tập hợp các phần tử trong dấu ngoặc vuông, sử dụng dấu chấm phẩy (;) để phân cách các phần tử.

c = [7;  8;  9;  10; 11]

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

c =
       7       
       8       
       9       
      10       
      11

Tạo ma trận

Ma trận là một mảng số hai chiều.

Trong MATLAB, một ma trận được tạo bằng cách nhập mỗi hàng dưới dạng một chuỗi các phần tử được phân tách bằng dấu cách hoặc dấu phẩy, và cuối hàng được phân cách bằng dấu chấm phẩy. Ví dụ: chúng ta hãy tạo ma trận 3 x 3 dưới dạng:

m = [1 2 3; 4 5 6; 7 8 9]

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

m =
       1              2              3       
       4              5              6       
       7              8              9

MATLAB là một chương trình tương tác để tính toán số và hiển thị dữ liệu. Bạn có thể nhập một lệnh bằng cách gõ nó vào dấu nhắc MATLAB '>>' trênCommand Window.

Trong phần này, chúng tôi sẽ cung cấp danh sách các lệnh MATLAB thường được sử dụng.

Các lệnh để quản lý một phiên

MATLAB cung cấp các lệnh khác nhau để quản lý một phiên. Bảng sau cung cấp tất cả các lệnh như vậy:

Chỉ huy	Mục đích
clc	Xóa cửa sổ lệnh.
thông thoáng	Loại bỏ các biến khỏi bộ nhớ.
hiện hữu	Kiểm tra sự tồn tại của tệp hoặc biến.
toàn cầu	Khai báo các biến là toàn cục.
Cứu giúp	Tìm kiếm một chủ đề trợ giúp.
tìm kiếm	Tìm kiếm các mục trợ giúp cho một từ khóa.
bỏ cuộc	Dừng MATLAB.
WHO	Liệt kê các biến hiện tại.
ai	Liệt kê các biến hiện tại (hiển thị dài).

Các lệnh làm việc với hệ thống

MATLAB cung cấp nhiều lệnh hữu ích khác nhau để làm việc với hệ thống, chẳng hạn như lưu công việc hiện tại trong không gian làm việc dưới dạng tệp và tải tệp sau.

Nó cũng cung cấp các lệnh khác nhau cho các hoạt động khác liên quan đến hệ thống như, hiển thị ngày tháng, liệt kê các tệp trong thư mục, hiển thị thư mục hiện tại, v.v.

Bảng sau đây hiển thị một số lệnh liên quan đến hệ thống thường được sử dụng:

Chỉ huy	Mục đích
CD	Thay đổi thư mục hiện tại.
ngày	Hiển thị ngày hiện tại.
xóa bỏ	Xóa một tệp.
Nhật ký	Bật / tắt ghi tệp nhật ký.
dir	Liệt kê tất cả các tệp trong thư mục hiện tại.
tải	Tải các biến không gian làm việc từ một tệp.
con đường	Hiển thị đường dẫn tìm kiếm.
pwd	Hiển thị thư mục hiện tại.
tiết kiệm	Lưu các biến không gian làm việc trong một tệp.
kiểu	Hiển thị nội dung của tệp.
gì	Liệt kê tất cả các tệp MATLAB trong thư mục hiện tại.
wklread	Đọc tệp bảng tính .wk1.

Lệnh đầu vào và đầu ra

MATLAB cung cấp các lệnh liên quan đến đầu vào và đầu ra sau:

Chỉ huy	Mục đích
vứt bỏ	Hiển thị nội dung của một mảng hoặc chuỗi.
fscanf	Đọc dữ liệu được định dạng từ một tệp.
định dạng	Kiểm soát định dạng hiển thị màn hình.
fprintf	Thực hiện ghi định dạng vào màn hình hoặc tệp.
đầu vào	Hiển thị lời nhắc và chờ đầu vào.
;	Ngăn chặn in lụa.

Các fscanf và fprintfcác lệnh hoạt động giống như các hàm C scanf và printf. Chúng hỗ trợ các mã định dạng sau:

Định dạng mã	Mục đích
%s	Định dạng dưới dạng một chuỗi.
%d	Định dạng dưới dạng số nguyên.
%f	Định dạng dưới dạng giá trị dấu phẩy động.
%e	Định dạng dưới dạng giá trị dấu phẩy động trong ký hiệu khoa học.
%g	Định dạng ở dạng nhỏ gọn nhất:% f hoặc% e.
\n	Chèn một dòng mới trong chuỗi đầu ra.
\t	Chèn một tab trong chuỗi đầu ra.

Hàm định dạng có các dạng sau được sử dụng để hiển thị số:

Chức năng định dạng	Hiển thị lên đến
định dạng ngắn	Bốn chữ số thập phân (mặc định).
định dạng dài	16 chữ số thập phân.
định dạng ngắn e	Năm chữ số cộng với số mũ.
định dạng dài e	16 chữ số cộng với số mũ.
định dạng ngân hàng	Hai chữ số thập phân.
định dạng +	Tích cực, tiêu cực hoặc bằng không.
định dạng chuột	Xấp xỉ hợp lý.
định dạng nhỏ gọn	Chặn một số nguồn cấp dữ liệu dòng.
định dạng lỏng lẻo	Đặt lại chế độ hiển thị nhỏ gọn hơn.

Lệnh vectơ, ma trận và mảng

Bảng sau đây cho thấy các lệnh khác nhau được sử dụng để làm việc với mảng, ma trận và vectơ:

Chỉ huy	Mục đích
con mèo	Nối các mảng.
tìm thấy	Tìm chỉ số của các phần tử khác không.
chiều dài	Tính số phần tử.
linspace	Tạo vectơ cách đều nhau.
logspace	Tạo vectơ khoảng cách theo lôgarit.
tối đa	Trả về phần tử lớn nhất.
min	Trả về phần tử nhỏ nhất.
thần đồng	Sản phẩm của từng cột.
định hình lại	Thay đổi kích thước.
kích thước	Tính toán kích thước mảng.
sắp xếp	Sắp xếp từng cột.
Tổng	Tính tổng mỗi cột.
con mắt	Tạo ma trận nhận dạng.
những cái	Tạo một loạt các cái.
số không	Tạo một mảng các số không.
vượt qua	Tính toán các sản phẩm chéo của ma trận.
dấu chấm	Tính toán sản phẩm chấm ma trận.
det	Tính định thức của một mảng.
inv	Tính toán nghịch đảo của ma trận.
pinv	Tính toán nghịch đảo giả của ma trận.
cấp	Tính toán hạng của ma trận.
rref	Tính toán biểu mẫu cấp độ hàng giảm.
ô	Tạo mảng ô.
celldisp	Hiển thị mảng ô.
cellplot	Hiển thị biểu diễn đồ họa của mảng ô.
num2cell	Chuyển đổi mảng số thành mảng ô.
thỏa thuận	Đối sánh danh sách đầu vào và đầu ra.
iscell	Xác định mảng ô.

Lệnh vẽ đồ thị

MATLAB cung cấp nhiều lệnh để vẽ đồ thị. Bảng sau đây cho thấy một số lệnh thường được sử dụng để vẽ biểu đồ:

Chỉ huy	Mục đích
trục	Đặt giới hạn trục.
fplot	Biểu đồ thông minh của các chức năng.
lưới	Hiển thị đường lưới.
âm mưu	Tạo ra ô xy.
in	In biểu đồ hoặc lưu biểu đồ vào một tệp.
tiêu đề	Đặt văn bản ở đầu cốt truyện.
xlabel	Thêm nhãn văn bản vào trục x.
ylabel	Thêm nhãn văn bản vào trục y.
rìu	Tạo các đối tượng trục.
đóng	Đóng cốt truyện hiện tại.
đóng tất cả	Đóng tất cả các âm mưu.
nhân vật	Mở một cửa sổ hình mới.
gtext	Cho phép đặt nhãn bằng chuột.
giữ	Đóng băng cốt truyện hiện tại.
huyền thoại	Vị trí chú giải bằng chuột.
Làm tươi	Vẽ lại cửa sổ hình hiện tại.
bộ	Chỉ định các thuộc tính của các đối tượng như trục.
subplot	Tạo các âm mưu trong các cửa sổ phụ.
bản văn	Chuỗi địa điểm trong hình.
quán ba	Tạo biểu đồ thanh.
nhật ký	Tạo cốt truyện nhật ký.
cực	Tạo ra âm mưu cực.
semilogx	Tạo cốt truyện semilog. (cơ số logarit).
semilogy	Tạo cốt truyện semilog. (hàm logarit).
cầu thang	Tạo âm mưu cầu thang.
thân cây	Tạo sơ đồ gốc.

Cho đến nay, chúng tôi đã sử dụng môi trường MATLAB như một máy tính. Tuy nhiên, MATLAB cũng là một ngôn ngữ lập trình mạnh mẽ, cũng như một môi trường tính toán tương tác.

Trong các chương trước, bạn đã học cách nhập lệnh từ dấu nhắc lệnh MATLAB. MATLAB cũng cho phép bạn viết một loạt lệnh vào một tệp và thực thi tệp dưới dạng đơn vị hoàn chỉnh, giống như viết một hàm và gọi nó.

Tệp M

MATLAB cho phép viết hai loại tệp chương trình:

• Scripts - tệp script là tệp chương trình có .m extension. Trong các tệp này, bạn viết một loạt lệnh mà bạn muốn thực hiện cùng nhau. Tập lệnh không chấp nhận đầu vào và không trả về bất kỳ đầu ra nào. Chúng hoạt động dựa trên dữ liệu trong không gian làm việc.

• Functions - tệp chức năng cũng là tệp chương trình với .m extension. Các hàm có thể chấp nhận đầu vào và trả về đầu ra. Các biến bên trong là cục bộ của hàm.

Bạn có thể sử dụng trình chỉnh sửa MATLAB hoặc bất kỳ trình soạn thảo văn bản nào khác để tạo .mcác tập tin. Trong phần này, chúng ta sẽ thảo luận về các tệp script. Một tệp kịch bản chứa nhiều dòng lệnh MATLAB tuần tự và các lệnh gọi hàm. Bạn có thể chạy một tập lệnh bằng cách gõ tên của nó vào dòng lệnh.

Tạo và chạy tệp script

Để tạo tệp kịch bản, bạn cần sử dụng trình soạn thảo văn bản. Bạn có thể mở trình chỉnh sửa MATLAB theo hai cách:

• Sử dụng dấu nhắc lệnh
• Sử dụng IDE

Nếu bạn đang sử dụng dấu nhắc lệnh, hãy nhập edittrong dấu nhắc lệnh. Thao tác này sẽ mở trình chỉnh sửa. Bạn có thể gõ trực tiếpedit và sau đó là tên tệp (có phần mở rộng .m)

edit 
Or
edit <filename>

Lệnh trên sẽ tạo tệp trong thư mục MATLAB mặc định. Nếu bạn muốn lưu trữ tất cả các tệp chương trình trong một thư mục cụ thể, thì bạn sẽ phải cung cấp toàn bộ đường dẫn.

Hãy để chúng tôi tạo một thư mục có tên là progs. Nhập các lệnh sau tại dấu nhắc lệnh (>>) -

mkdir progs    % create directory progs under default directory
chdir progs    % changing the current directory to progs
edit  prog1.m  % creating an m file named prog1.m

Nếu bạn đang tạo tệp lần đầu tiên, MATLAB sẽ nhắc bạn xác nhận tệp đó. Nhấp vào Có.

Ngoài ra, nếu bạn đang sử dụng IDE, hãy chọn MỚI -> Tập lệnh. Thao tác này cũng mở trình chỉnh sửa và tạo tệp có tên Untitled. Bạn có thể đặt tên và lưu tệp sau khi nhập mã.

Nhập mã sau vào trình chỉnh sửa -

NoOfStudents = 6000;
TeachingStaff = 150;
NonTeachingStaff = 20;
Total = NoOfStudents + TeachingStaff ...
   + NonTeachingStaff;
disp(Total);

Sau khi tạo và lưu tệp, bạn có thể chạy nó theo hai cách:

• Nhấp vào Run trên cửa sổ trình chỉnh sửa hoặc

• Chỉ cần nhập tên tệp (không có phần mở rộng) trong dấu nhắc lệnh: >> prog1

Cửa sổ lệnh nhắc nhở hiển thị kết quả:

6170

Thí dụ

Tạo một tệp kịch bản và nhập mã sau:

a = 5; b = 7;
c = a + b
d = c + sin(b)
e = 5 * d
f = exp(-d)

Khi đoạn mã trên được biên dịch và thực thi, nó tạo ra kết quả sau:

c =  12
d =  12.657
e =  63.285
f =    3.1852e-06

MATLAB không yêu cầu bất kỳ khai báo kiểu hoặc câu lệnh thứ nguyên nào. Bất cứ khi nào MATLAB gặp một tên biến mới, nó sẽ tạo biến đó và cấp phát không gian bộ nhớ thích hợp.

Nếu biến đã tồn tại, thì MATLAB sẽ thay thế nội dung gốc bằng nội dung mới và phân bổ không gian lưu trữ mới, nếu cần.

Ví dụ,

Total = 42

Câu lệnh trên tạo một ma trận 1-1 có tên là 'Tổng' và lưu giá trị 42 trong đó.

Các loại dữ liệu có sẵn trong MATLAB

MATLAB cung cấp 15 kiểu dữ liệu cơ bản. Mọi kiểu dữ liệu đều lưu trữ dữ liệu ở dạng ma trận hoặc mảng. Kích thước của ma trận hoặc mảng này tối thiểu là 0 x 0 và kích thước này có thể tăng lên thành ma trận hoặc mảng có kích thước bất kỳ.

Bảng sau đây cho thấy các kiểu dữ liệu được sử dụng phổ biến nhất trong MATLAB:

Sr.No.	Loại dữ liệu và mô tả
1	int8 Số nguyên có dấu 8 bit
2	uint8 Số nguyên không dấu 8 bit
3	int16 Số nguyên có dấu 16 bit
4	uint16 Số nguyên không dấu 16 bit
5	int32 Số nguyên có dấu 32 bit
6	uint32 Số nguyên không dấu 32 bit
7	int64 Số nguyên có dấu 64 bit
số 8	uint64 Số nguyên không dấu 64 bit
9	single dữ liệu số chính xác đơn
10	double dữ liệu số chính xác kép
11	logical giá trị lôgic của 1 hoặc 0, đại diện cho đúng và sai tương ứng
12	char dữ liệu ký tự (chuỗi được lưu trữ dưới dạng vectơ của ký tự)
13	cell array mảng các ô được lập chỉ mục, mỗi ô có khả năng lưu trữ một mảng có kích thước và kiểu dữ liệu khác nhau
14	structure Cấu trúc giống C, mỗi cấu trúc có các trường được đặt tên có khả năng lưu trữ một mảng có kích thước và kiểu dữ liệu khác nhau
15	function handle con trỏ đến một hàm
16	user classes các đối tượng được xây dựng từ một lớp do người dùng xác định
17	java classes các đối tượng được xây dựng từ một lớp Java

Thí dụ

Tạo tệp kịch bản với mã sau:

str = 'Hello World!'
n = 2345
d = double(n)
un = uint32(789.50)
rn = 5678.92347
c = int32(rn)

Khi đoạn mã trên được biên dịch và thực thi, nó tạo ra kết quả sau:

str = Hello World!
n =  2345
d =  2345
un = 790
rn = 5678.9
c =  5679

Chuyển đổi loại dữ liệu

MATLAB cung cấp các chức năng khác nhau để chuyển đổi, một giá trị từ kiểu dữ liệu này sang kiểu dữ liệu khác. Bảng sau đây cho thấy các hàm chuyển đổi kiểu dữ liệu:

Chức năng	Mục đích
char	Chuyển đổi thành mảng ký tự (chuỗi)
int2str	Chuyển đổi dữ liệu số nguyên thành chuỗi
mat2str	Chuyển đổi ma trận thành chuỗi
num2str	Chuyển đổi số thành chuỗi
str2double	Chuyển đổi chuỗi thành giá trị chính xác kép
str2num	Chuyển chuỗi thành số
native2unicode	Chuyển đổi byte số thành ký tự Unicode
unicode2native	Chuyển đổi các ký tự Unicode sang byte số
base2dec	Chuyển chuỗi số cơ sở N thành số thập phân
bin2dec	Chuyển đổi chuỗi số nhị phân thành số thập phân
dec2base	Chuyển đổi số thập phân sang số cơ số N trong chuỗi
dec2bin	Chuyển đổi số thập phân sang số nhị phân trong chuỗi
dec2hex	Chuyển đổi số thập phân sang số thập lục phân trong chuỗi
hex2dec	Chuyển đổi chuỗi số thập lục phân thành số thập phân
hex2num	Chuyển đổi chuỗi số thập lục phân thành số chính xác kép
num2hex	Chuyển đổi đơn và đôi sang chuỗi thập lục phân IEEE
cell2mat	Chuyển đổi mảng ô thành mảng số
cell2struct	Chuyển đổi mảng ô thành mảng cấu trúc
cellstr	Tạo mảng ô của chuỗi từ mảng ký tự
mat2cell	Chuyển đổi mảng thành mảng ô với các ô có kích thước khác nhau
num2cell	Chuyển đổi mảng thành mảng ô với các ô có kích thước nhất quán
struct2cell	Chuyển đổi cấu trúc thành mảng ô

Xác định kiểu dữ liệu

MATLAB cung cấp các chức năng khác nhau để xác định kiểu dữ liệu của một biến.

Bảng sau cung cấp các hàm để xác định kiểu dữ liệu của một biến:

Chức năng	Mục đích
Là	Phát hiện trạng thái
là một	Xác định xem đầu vào có phải là đối tượng của lớp được chỉ định hay không
iscell	Xác định xem đầu vào có phải là mảng ô hay không
iscellstr	Xác định xem đầu vào có phải là mảng ô của chuỗi hay không
ischar	Xác định xem mục có phải là mảng ký tự không
isfield	Xác định xem đầu vào có phải là trường mảng cấu trúc hay không
isfloat	Xác định xem đầu vào có phải là mảng dấu phẩy động không
ishghandle	True for Handle Graphics xử lý đối tượng đồ họa
isinteger	Xác định xem đầu vào là mảng số nguyên
isjava	Xác định xem đầu vào là đối tượng Java
thần học	Xác định xem đầu vào là mảng logic
isnumeric	Xác định xem đầu vào là mảng số
isobject	Xác định xem đầu vào là đối tượng MATLAB
là thật	Kiểm tra xem đầu vào có phải là mảng thực không
Isscalar	Xác định xem đầu vào có vô hướng không
isstr	Xác định xem đầu vào là mảng ký tự
cấu trúc	Xác định xem đầu vào là mảng cấu trúc
isvector	Xác định xem đầu vào là vectơ
lớp học	Xác định lớp đối tượng
xác thực	Kiểm tra tính hợp lệ của mảng
ai	Liệt kê các biến trong không gian làm việc, với kích thước và kiểu

Thí dụ

Tạo tệp kịch bản với mã sau:

x = 3
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
 
x = 23.54
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
 
x = [1 2 3]
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
 
x = 'Hello'
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)

Khi bạn chạy tệp, nó tạo ra kết quả sau:

x = 3
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x = 23.540
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x =

          1          2          3

ans = 0
ans = 1
ans = 1
ans = 0
x = Hello
ans = 0
ans = 0
ans = 1
ans = 0
ans = 0

Một toán tử là một ký hiệu yêu cầu trình biên dịch thực hiện các thao tác toán học hoặc logic cụ thể. MATLAB được thiết kế để hoạt động chủ yếu trên toàn bộ ma trận và mảng. Do đó, các toán tử trong MATLAB hoạt động trên cả dữ liệu vô hướng và không vô hướng. MATLAB cho phép các loại hoạt động cơ bản sau:

• Toán tử số học
• Toán tử quan hệ
• Toán tử logic
• Hoạt động Bitwise
• Đặt hoạt động

Toán tử số học

MATLAB cho phép hai loại phép toán số học khác nhau -

• Phép toán số học ma trận
• Phép toán số học mảng

Các phép toán số học ma trận giống như được định nghĩa trong đại số tuyến tính. Các phép toán mảng được thực thi từng phần tử, cả trên mảng một chiều và nhiều chiều.

Các toán tử ma trận và toán tử mảng được phân biệt bằng ký hiệu dấu chấm (.). Tuy nhiên, vì phép toán cộng và trừ giống nhau đối với ma trận và mảng, nên toán tử giống nhau cho cả hai trường hợp. Bảng sau đây mô tả ngắn gọn về các toán tử:

Hiển thị các ví dụ

Sr.No.	Nhà điều hành & Mô tả
1	+ Phép cộng hoặc cộng một bậc. A + B thêm các giá trị được lưu trữ trong các biến A và B. A và B phải có cùng kích thước, trừ khi một là vô hướng. Một đại lượng vô hướng có thể được thêm vào ma trận có kích thước bất kỳ.
2	- Phép trừ hoặc trừ một bậc. AB trừ giá trị của B cho A. A và B phải có cùng kích thước, trừ khi một là vô hướng. Một đại lượng vô hướng có thể được trừ khỏi một ma trận có kích thước bất kỳ.
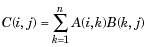
3	* Phép nhân ma trận. C = A * B là tích đại số tuyến tính của ma trận A và B. Chính xác hơn, Đối với A và B không vô hướng, số cột của A phải bằng số hàng của B. Một vô hướng có thể nhân một ma trận có kích thước bất kỳ.
4	.* Phép nhân mảng. A. * B là tích từng phần tử của mảng A và B. A và B phải có cùng kích thước, trừ khi một trong số chúng là vô hướng.
5	/ Gạch chéo hoặc phân chia bên phải ma trận. B / A gần giống với B * inv (A). Chính xác hơn, B / A = (A '\ B') '.
6	./ Phép chia phải mảng. A./B là ma trận có các phần tử A (i, j) / B (i, j). A và B phải có cùng kích thước, trừ khi một trong số chúng là vô hướng.
7	\ Dấu gạch chéo ngược hoặc phép chia trái ma trận. Nếu A là ma trận vuông, A \ B gần giống với inv (A) * B, ngoại trừ nó được tính theo một cách khác. Nếu A là một n-by-n ma trận và B là một vector cột với các thành phần n, hay một ma trận với một số cột như vậy, sau đó X = A \ B là giải pháp cho phương trình AX = B . Một thông báo cảnh báo được hiển thị nếu A có tỷ lệ kém hoặc gần như số ít.
số 8	.\ Mảng chia trái. A. \ B là ma trận có các phần tử B (i, j) / A (i, j). A và B phải có cùng kích thước, trừ khi một trong số chúng là vô hướng.
9	^ Quyền lực ma trận. X ^ p là X thành lũy thừa p, nếu p là một vô hướng. Nếu p là số nguyên, lũy thừa được tính bằng bình phương lặp lại. Nếu số nguyên là số âm thì X được đảo ngược trước. Đối với các giá trị khác của p, phép tính liên quan đến giá trị riêng và giá trị riêng, sao cho nếu [V, D] = eig (X), thì X ^ p = V * D. ^ p / V.
10	.^ Sức mạnh mảng. A. ^ B là ma trận có các phần tử A (i, j) thành lũy thừa B (i, j). A và B phải có cùng kích thước, trừ khi một trong số chúng là vô hướng.
11	' Chuyển vị ma trận. A 'là phép chuyển vị đại số tuyến tính của A. Đối với ma trận phức, đây là phép chuyển vị liên hợp phức.
12	.' Chuyển vị mảng. A. ' là mảng chuyển vị của A. Đối với ma trận phức, điều này không liên quan đến phép cộng hợp.

Toán tử quan hệ

Toán tử quan hệ cũng có thể hoạt động trên cả dữ liệu vô hướng và không vô hướng. Toán tử quan hệ cho mảng thực hiện so sánh từng phần tử giữa hai mảng và trả về một mảng logic có cùng kích thước, với các phần tử được đặt thành lôgic 1 (true) trong đó quan hệ là đúng và các phần tử được đặt thành lôgic 0 (sai) ở đó không phải.

Bảng sau đây cho thấy các toán tử quan hệ có sẵn trong MATLAB:

Hiển thị các ví dụ

Sr.No.	Nhà điều hành & Mô tả
1	< Ít hơn
2	<= Ít hơn hoặc bằng
3	> Lớn hơn
4	>= Lớn hơn hoặc bằng
5	== Tương đương với
6	~= Không bằng

Toán tử logic

MATLAB cung cấp hai loại toán tử và hàm logic -

• Phần tử khôn ngoan - Các toán tử này hoạt động trên các phần tử tương ứng của mảng logic.

• Ngắn mạch - Các toán tử này hoạt động trên các biểu thức vô hướng và logic.

Các toán tử logic khôn ngoan hoạt động theo từng phần tử trên mảng logic. Các ký hiệu &, |, và ~ là các toán tử mảng logic AND, OR và NOT.

Các toán tử logic ngắn mạch cho phép đoản mạch trên các hoạt động logic. Các ký hiệu && và || là các toán tử ngắn mạch logic AND và OR.

Hiển thị các ví dụ

Hoạt động Bitwise

Toán tử bitwise làm việc trên các bit và thực hiện hoạt động từng bit. Bảng sự thật cho &, |, và ^ như sau:

p	q	p & q	p | q	p ^ q
0	0	0	0	0
0	1	0	1	1
1	1	1	1	0
1	0	0	1	1

Giả sử nếu A = 60; và B = 13; Bây giờ ở định dạng nhị phân, chúng sẽ như sau:

A = 0011 1100

B = 0000 1101

-----------------

A&B = 0000 1100

A | B = 0011 1101

A ^ B = 0011 0001

~ A = 1100 0011

MATLAB cung cấp các chức năng khác nhau cho các hoạt động theo bit như hoạt động 'bitwise và', 'theo chiều bit hoặc' và 'không theo chiều bit', hoạt động shift, v.v.

Bảng sau đây cho thấy các phép toán bitwise thường được sử dụng:

Hiển thị các ví dụ

Chức năng	Mục đích
bitand (a, b)	Bit-khôn ngoan AND của số nguyên a và b
bitcmp (a)	Sự bổ sung khôn ngoan của một
bitget (a, pos)	Nhận bit tại vị trí xác định pos , trong mảng số nguyên a
bitor (a, b)	OR-khôn ngoan của số nguyên a và b
bitet (a, pos)	Set bit tại địa điểm cụ thể pos của một
dịch chuyển bit (a, k)	Trả về một chuyển sang trái k bit, tương đương với nhân với 2 k . Giá trị âm của k tương ứng với các bit dịch sang phải hoặc chia cho 2 | k | và làm tròn đến số nguyên gần nhất theo hướng âm vô hạn. Bất kỳ bit tràn nào đều bị cắt bớt.
bitxor (a, b)	XOR bit khôn ngoan của số nguyên a và b
hoán đổi	Trao đổi thứ tự byte

Đặt hoạt động

MATLAB cung cấp các chức năng khác nhau cho các hoạt động tập hợp, như liên hợp, giao điểm và kiểm tra thành viên tập hợp, v.v.

Bảng sau đây cho thấy một số hoạt động tập hợp thường được sử dụng:

Hiển thị các ví dụ

Sr.No.	Mô tả chức năng
1	intersect(A,B) Đặt giao điểm của hai mảng; trả về các giá trị chung cho cả A và B. Các giá trị trả về được sắp xếp theo thứ tự.
2	intersect(A,B,'rows') Xử lý mỗi hàng A và mỗi hàng B là các thực thể đơn lẻ và trả về các hàng chung cho cả A và B. Các hàng của ma trận trả về được sắp xếp theo thứ tự.
3	ismember(A,B) Trả về một mảng có cùng kích thước với A, chứa 1 (true) trong đó các phần tử của A được tìm thấy trong B. Ở những nơi khác, nó trả về 0 (false).
4	ismember(A,B,'rows') Xử lý mỗi hàng A và mỗi hàng B là các thực thể đơn lẻ và trả về một vectơ chứa 1 (đúng) trong đó các hàng của ma trận A cũng là các hàng B. Ở những nơi khác, nó trả về 0 (sai).
5	issorted(A) Trả về lôgic 1 (đúng) nếu các phần tử của A theo thứ tự được sắp xếp và lôgic 0 (sai) nếu ngược lại. Đầu vào A có thể là một vectơ hoặc một mảng ô N-x-1 hoặc 1-x-N gồm các chuỗi.A is considered to be sorted if A và đầu ra của sắp xếp (A) là bằng nhau.
6	issorted(A, 'rows') Trả về lôgic 1 (đúng) nếu các hàng của ma trận hai chiều A theo thứ tự được sắp xếp và lôgic 0 (sai) nếu ngược lại. Matrix A is considered to be sorted if A và đầu ra của máy sắp xếp (A) bằng nhau.
7	setdiff(A,B) Đặt hiệu của hai mảng; trả về các giá trị trong A không có trong B. Các giá trị trong mảng được trả về được sắp xếp theo thứ tự.
số 8	setdiff(A,B,'rows') Xử lý mỗi hàng A và mỗi hàng B là các thực thể đơn lẻ và trả về các hàng từ A không có trong B. Các hàng của ma trận trả về được sắp xếp theo thứ tự. Tùy chọn 'hàng' không hỗ trợ mảng ô.
9	setxor Đặt OR riêng của hai mảng
10	union Đặt sự kết hợp của hai mảng
11	unique Giá trị duy nhất trong mảng

Cấu trúc ra quyết định yêu cầu người lập trình phải chỉ định một hoặc nhiều điều kiện để được đánh giá hoặc kiểm tra bởi chương trình, cùng với một câu lệnh hoặc các câu lệnh sẽ được thực thi nếu điều kiện được xác định là đúng, và tùy chọn, các câu lệnh khác sẽ được thực thi nếu điều kiện được xác định là sai.

Sau đây là dạng chung của cấu trúc ra quyết định điển hình được tìm thấy trong hầu hết các ngôn ngữ lập trình:

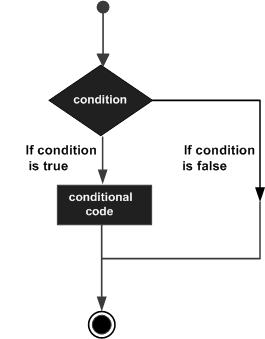
MATLAB cung cấp các loại câu lệnh ra quyết định sau. Nhấp vào các liên kết sau để kiểm tra chi tiết của chúng -

Sr.No.	Tuyên bố & Mô tả
1	nếu ... kết thúc câu lệnh An if ... end statement bao gồm một biểu thức boolean theo sau bởi một hoặc nhiều câu lệnh.
2	if ... else ... kết thúc câu lệnh An if statement có thể được theo sau bởi một tùy chọn else statement, thực thi khi biểu thức boolean sai.
3	Câu lệnh kết thúc if ... elseif ... elseif ... else ... An if câu lệnh có thể được theo sau bởi một (hoặc nhiều) tùy chọn elseif... và một else , rất hữu ích để kiểm tra các điều kiện khác nhau.
4	câu lệnh if lồng nhau Bạn có thể sử dụng một if hoặc là elseif tuyên bố bên trong khác if hoặc là elseif các câu lệnh).
5	chuyển đổi tuyên bố A switch câu lệnh cho phép một biến được kiểm tra tính bình đẳng với một danh sách các giá trị.
6	các câu lệnh chuyển đổi lồng nhau Bạn có thể sử dụng một switch tuyên bố bên trong khác switch các câu lệnh).

Có thể có một tình huống khi bạn cần thực thi một khối mã nhiều lần. Nói chung, các câu lệnh được thực hiện tuần tự. Câu lệnh đầu tiên trong một hàm được thực thi đầu tiên, tiếp theo là câu lệnh thứ hai, v.v.

Các ngôn ngữ lập trình cung cấp các cấu trúc điều khiển khác nhau cho phép các đường dẫn thực thi phức tạp hơn.

Câu lệnh lặp cho phép chúng ta thực hiện một câu lệnh hoặc một nhóm câu lệnh nhiều lần và sau đây là dạng chung của câu lệnh lặp trong hầu hết các ngôn ngữ lập trình:

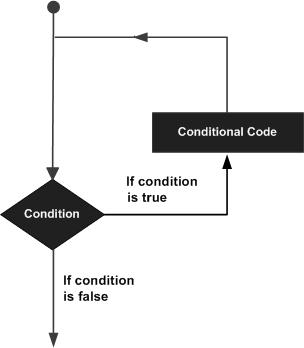
MATLAB cung cấp các loại vòng lặp sau để xử lý các yêu cầu về vòng lặp. Nhấp vào các liên kết sau để kiểm tra chi tiết của chúng -

Sr.No.	Loại vòng lặp & Mô tả
1	trong khi lặp lại Lặp lại một câu lệnh hoặc một nhóm câu lệnh trong khi một điều kiện đã cho là đúng. Nó kiểm tra điều kiện trước khi thực thi phần thân của vòng lặp.
2	vòng lặp for Thực thi một chuỗi các câu lệnh nhiều lần và viết tắt mã quản lý biến vòng lặp.
3	vòng lồng nhau Bạn có thể sử dụng một hoặc nhiều vòng lặp bên trong bất kỳ vòng lặp nào khác.

Tuyên bố kiểm soát vòng lặp

Các câu lệnh điều khiển vòng lặp thay đổi việc thực thi từ trình tự bình thường của nó. Khi việc thực thi rời khỏi một phạm vi, tất cả các đối tượng tự động được tạo trong phạm vi đó sẽ bị phá hủy.

MATLAB hỗ trợ các câu lệnh điều khiển sau. Nhấp vào các liên kết sau để kiểm tra chi tiết của chúng.

Sr.No.	Tuyên bố & Mô tả Kiểm soát
1	tuyên bố ngắt Chấm dứt loop câu lệnh và chuyển việc thực thi câu lệnh ngay sau vòng lặp.
2	tiếp tục tuyên bố Làm cho vòng lặp bỏ qua phần còn lại của phần thân và ngay lập tức kiểm tra lại tình trạng của nó trước khi nhắc lại.

Vectơ là một mảng số một chiều. MATLAB cho phép tạo hai loại vectơ:

• Vectơ hàng
• Vectơ cột

Vectơ hàng

Row vectors được tạo bằng cách đặt tập hợp các phần tử trong dấu ngoặc vuông, sử dụng dấu cách hoặc dấu phẩy để phân cách các phần tử.

r = [7 8 9 10 11]

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

r =

   7    8    9   10   11

Vectơ cột

Column vectors được tạo bằng cách đặt tập hợp các phần tử trong dấu ngoặc vuông, sử dụng dấu chấm phẩy để phân tách các phần tử.

c = [7;  8;  9;  10; 11]

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

c =
      7       
      8       
      9       
      10       
      11

Tham chiếu các phần tử của một vectơ

Bạn có thể tham chiếu một hoặc nhiều phần tử của vectơ theo một số cách. Thành phần ^thứ i của vectơ v được gọi là v (i). Ví dụ -

v = [ 1; 2; 3; 4; 5; 6];	% creating a column vector of 6 elements
v(3)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =  3

Khi bạn tham chiếu một vectơ có dấu hai chấm, chẳng hạn như v (:), tất cả các thành phần của vectơ được liệt kê.

v = [ 1; 2; 3; 4; 5; 6];	% creating a column vector of 6 elements
v(:)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
     1
     2
     3
     4
     5
     6

MATLAB cho phép bạn chọn một loạt các phần tử từ một vectơ.

Ví dụ: chúng ta hãy tạo một vectơ hàng rv gồm 9 phần tử, sau đó chúng tôi sẽ tham chiếu các phần tử từ 3 đến 7 bằng cách viếtrv(3:7)và tạo một vectơ mới có tên là sub_rv .

rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

sub_rv =

   3   4   5   6   7

Hoạt động Vector

Trong phần này, chúng ta hãy thảo luận về các phép toán vectơ sau:

• Phép cộng và phép trừ vectơ

• Nhân vô hướng của vectơ

• Chuyển vị của một vectơ

• Vectơ nối

• Tầm quan trọng của một vectơ

• Sản phẩm chấm vector

• Vectơ có các phần tử có khoảng cách đồng nhất

Ma trận là một mảng số hai chiều.

Trong MATLAB, bạn tạo ma trận bằng cách nhập các phần tử trong mỗi hàng dưới dạng dấu phẩy hoặc số được phân cách bằng dấu cách và sử dụng dấu chấm phẩy để đánh dấu phần cuối của mỗi hàng.

Ví dụ, chúng ta hãy tạo một ma trận 4 x 5 a -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

a =
      1     2     3     4     5
      2     3     4     5     6
      3     4     5     6     7
      4     5     6     7     8

Tham chiếu các yếu tố của ma trận

Để tham chiếu đến một phần tử trong hàng ^thứ m và cột ^thứ n , của ma trận mx , chúng ta viết:

mx(m, n);

Ví dụ, để tham chiếu đến phần tử ở hàng ^{thứ 2} và cột ^thứ 5 của ma trận a , như đã tạo trong phần trước, chúng ta nhập:

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(2,5)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =  6

Để tham chiếu đến tất cả các phần tử trong cột ^thứ m, chúng ta gõ A (:, m).

Hãy để chúng tôi tạo một vectơ cột v, từ các phần tử của hàng ^thứ 4 của ma trận a -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
v = a(:,4)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

v =
      4
      5
      6
      7

Bạn cũng có thể chọn các phần tử trong cột ^thứ m đến cột ^thứ n , vì điều này chúng tôi viết:

a(:,m:n)

Hãy để chúng tôi tạo một ma trận nhỏ hơn lấy các phần tử từ cột thứ hai và thứ ba -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
      2     3
      3     4
      4     5
      5     6

Theo cách tương tự, bạn có thể tạo ma trận con lấy một phần con của ma trận.

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
      2     3
      3     4
      4     5
      5     6

Theo cách tương tự, bạn có thể tạo ma trận con lấy một phần con của ma trận.

Ví dụ, chúng ta hãy tạo một ma trận con sa lấy phần con bên trong của một -

3     4     5     
4     5     6

Để làm điều này, hãy viết -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
sa = a(2:3,2:4)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

sa =
      3     4     5
      4     5     6

Xóa hàng hoặc cột trong ma trận

Bạn có thể xóa toàn bộ hàng hoặc cột của ma trận bằng cách gán một tập hợp trống dấu ngoặc vuông [] cho hàng hoặc cột đó. Về cơ bản, [] biểu thị một mảng trống.

Ví dụ: chúng ta hãy xóa hàng thứ tư của -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a( 4 , : ) = []

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

a =
      1     2     3     4     5
      2     3     4     5     6
      3     4     5     6     7

Tiếp theo, chúng ta hãy xóa cột thứ năm của -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(: , 5)=[]

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

a =
      1     2     3     4
      2     3     4     5
      3     4     5     6
      4     5     6     7

Thí dụ

Trong ví dụ này, chúng ta hãy tạo một ma trận 3 x 3 m, sau đó chúng ta sẽ sao chép hàng thứ hai và thứ ba của ma trận này hai lần để tạo ma trận 4 x 3.

Tạo tệp kịch bản với mã sau:

a = [ 1 2 3 ; 4 5 6; 7 8 9];
new_mat = a([2,3,2,3],:)

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

new_mat =
      4     5     6
      7     8     9
      4     5     6
      7     8     9

Hoạt động ma trận

Trong phần này, chúng ta hãy thảo luận về các phép toán ma trận cơ bản và thường được sử dụng sau đây:

• Phép cộng và phép trừ ma trận

• Phân chia ma trận

• Phép toán vô hướng của ma trận

• Chuyển vị của một ma trận

• Kết hợp ma trận

• Phép nhân ma trận

• Yếu tố quyết định của ma trận

• Nghịch đảo của ma trận

Tất cả các biến của tất cả các kiểu dữ liệu trong MATLAB đều là mảng nhiều chiều. Vectơ là mảng một chiều và ma trận là mảng hai chiều.

Chúng ta đã thảo luận về vectơ và ma trận. Trong chương này, chúng ta sẽ thảo luận về mảng nhiều chiều. Tuy nhiên, trước đó, chúng ta hãy thảo luận về một số loại mảng đặc biệt.

Mảng đặc biệt trong MATLAB

Trong phần này, chúng ta sẽ thảo luận về một số hàm tạo một số mảng đặc biệt. Đối với tất cả các hàm này, một đối số duy nhất tạo ra mảng vuông, đối số kép tạo mảng hình chữ nhật.

Các zeros() hàm tạo một mảng tất cả các số không -

Ví dụ -

zeros(5)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
      0     0     0     0     0
      0     0     0     0     0
      0     0     0     0     0
      0     0     0     0     0
      0     0     0     0     0

Các ones() hàm tạo một mảng gồm tất cả những cái -

Ví dụ -

ones(4,3)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
      1     1     1
      1     1     1
      1     1     1
      1     1     1

Các eye() chức năng tạo một ma trận nhận dạng.

Ví dụ -

eye(4)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
      1     0     0     0
      0     1     0     0
      0     0     1     0
      0     0     0     1

Các rand() hàm tạo một mảng các số ngẫu nhiên được phân phối đồng đều trên (0,1) -

Ví dụ -

rand(3, 5)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   0.8147    0.9134    0.2785    0.9649    0.9572
   0.9058    0.6324    0.5469    0.1576    0.4854
   0.1270    0.0975    0.9575    0.9706    0.8003

A Magic Square

A magic square là một hình vuông tạo ra cùng một tổng, khi các phần tử của nó được thêm vào theo hàng, theo cột hoặc theo đường chéo.

Các magic()hàm tạo một mảng vuông kỳ diệu. Nó có một đối số số ít để cung cấp kích thước của hình vuông. Đối số phải là một đại lượng vô hướng lớn hơn hoặc bằng 3.

magic(4)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   16     2     3    13
   5    11    10     8
   9     7     6    12
   4    14    15     1

Mảng đa chiều

Mảng có nhiều hơn hai chiều được gọi là mảng nhiều chiều trong MATLAB. Mảng nhiều chiều trong MATLAB là phần mở rộng của ma trận hai chiều thông thường.

Nói chung để tạo một mảng nhiều chiều, trước tiên chúng ta tạo một mảng hai chiều và mở rộng nó.

Ví dụ, hãy tạo một mảng hai chiều a.

a = [7 9 5; 6 1 9; 4 3 2]

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

a =
   7     9     5
   6     1     9
   4     3     2

Mảng a là mảng 3 x 3; chúng ta có thể thêm thứ nguyên thứ ba vào a , bằng cách cung cấp các giá trị như -

a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

a =

ans(:,:,1) =

   0   0   0
   0   0   0
   0   0   0

ans(:,:,2) =

   1   2   3
   4   5   6
   7   8   9

Chúng ta cũng có thể tạo mảng nhiều chiều bằng cách sử dụng các hàm ones (), zeros () hoặc rand ().

Ví dụ,

b = rand(4,3,2)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

b(:,:,1) =
   0.0344    0.7952    0.6463
   0.4387    0.1869    0.7094
   0.3816    0.4898    0.7547
   0.7655    0.4456    0.2760

b(:,:,2) =
   0.6797    0.4984    0.2238
   0.6551    0.9597    0.7513
   0.1626    0.3404    0.2551
   0.1190    0.5853    0.5060

Chúng tôi cũng có thể sử dụng cat()chức năng xây dựng mảng nhiều chiều. Nó nối danh sách các mảng dọc theo một thứ nguyên cụ thể -

Cú pháp cho hàm cat () là -

B = cat(dim, A1, A2...)

Ở đâu,

• B là mảng mới được tạo

• A1 , A2 , ... là các mảng được nối

• dim là thứ nguyên để nối các mảng với nhau

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

a = [9 8 7; 6 5 4; 3 2 1];
b = [1 2 3; 4 5 6; 7 8 9];
c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])

Khi bạn chạy tệp, nó sẽ hiển thị -

c(:,:,1) =
      9     8     7
      6     5     4
      3     2     1
c(:,:,2) =
      1     2     3
      4     5     6
      7     8     9
c(:,:,3) =
      2     3     1
      4     7     8
      3     9     0

Hàm mảng

MATLAB cung cấp các hàm sau để sắp xếp, xoay, hoán vị, định hình lại hoặc thay đổi nội dung mảng.

Chức năng	Mục đích
chiều dài	Chiều dài của vectơ hoặc kích thước mảng lớn nhất
ndims	Số kích thước mảng
numel	Số phần tử mảng
kích thước	Kích thước mảng
iscolumn	Xác định xem đầu vào có phải là vectơ cột hay không
isempty	Xác định xem mảng có trống không
ismatrix	Xác định xem đầu vào có phải là ma trận hay không
đất hoang	Xác định xem đầu vào có phải là vectơ hàng hay không
Isscalar	Xác định xem đầu vào có phải là vô hướng hay không
isvector	Xác định xem đầu vào có phải là vectơ hay không
blkdiag	Xây dựng khối ma trận đường chéo từ các đối số đầu vào
sự dịch chuyển vòng tròn	Chuyển mảng theo hình tròn
ctranspose	Chuyển vị liên hợp phức tạp
đường chéo	Ma trận đường chéo và đường chéo của ma trận
flipdim	Lật mảng dọc theo kích thước được chỉ định
flipplr	Lật ma trận từ trái sang phải
flipud	Lật ma trận lên xuống
ipermute	Đảo ngược kích thước hoán vị của mảng ND
hoán vị	Sắp xếp lại kích thước của mảng ND
quay lại	Bản sao và mảng lát
định hình lại	Định hình lại mảng
thối90	Xoay ma trận 90 độ
shiftdim	Thay đổi kích thước
được sắp xếp	Xác định xem các phần tử tập hợp có theo thứ tự được sắp xếp hay không
sắp xếp	Sắp xếp các phần tử mảng theo thứ tự tăng dần hoặc giảm dần
máy phân loại	Sắp xếp các hàng theo thứ tự tăng dần
vắt kiệt	Loại bỏ các kích thước singleton
đổi chỗ	Transpose
vectơ hóa	Vectơ hóa biểu thức

Ví dụ

Các ví dụ sau minh họa một số chức năng được đề cập ở trên.

Length, Dimension and Number of elements −

Tạo một tệp script và nhập mã sau vào đó:

x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9];
length(x)      % length of x vector
y = rand(3, 4, 5, 2);
ndims(y)       % no of dimensions in array y
s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab'];
numel(s)       % no of elements in s

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans =  8
ans =  4
ans =  23

Circular Shifting of the Array Elements −

Tạo một tệp script và nhập mã sau vào đó:

a = [1 2 3; 4 5 6; 7 8 9]  % the original array a
b = circshift(a,1)         %  circular shift first dimension values down by 1.
c = circshift(a,[1 -1])    % circular shift first dimension values % down by 1 
                           % and second dimension values to the left % by 1.

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

a =
   1     2     3
   4     5     6
   7     8     9

b =
   7     8     9
   1     2     3
   4     5     6

c =
   8     9     7
   2     3     1
   5     6     4

Sắp xếp Mảng

Tạo một tệp script và nhập mã sau vào đó:

v = [ 23 45 12 9 5 0 19 17]  % horizontal vector
sort(v)                      % sorting v
m = [2 6 4; 5 3 9; 2 0 1]    % two dimensional array
sort(m, 1)                   % sorting m along the row
sort(m, 2)                   % sorting m along the column

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

v =
   23    45    12     9     5     0    19    17
ans =
   0     5     9    12    17    19    23    45
m =
   2     6     4
   5     3     9
   2     0     1
ans =
   2     0     1
   2     3     4
   5     6     9
ans =
   2     4     6
   3     5     9
   0     1     2

Mảng ô

Mảng ô là mảng các ô được lập chỉ mục trong đó mỗi ô có thể lưu trữ một mảng có kích thước và kiểu dữ liệu khác nhau.

Các cellđược sử dụng để tạo một mảng ô. Cú pháp cho hàm ô là -

C = cell(dim)
C = cell(dim1,...,dimN)
D = cell(obj)

Ở đâu,

• C là mảng ô;

• dim là số nguyên vô hướng hoặc vectơ của số nguyên xác định kích thước của mảng ô C;

• dim1, ..., dimN là các số nguyên vô hướng xác định kích thước của C;

• obj là Một trong những điều sau:

  • Mảng hoặc đối tượng Java
  • Mảng .NET kiểu System.String hoặc System.Object

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

c = cell(2, 5);
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

c = 
{
   [1,1] = Red
   [2,1] =  1
   [1,2] = Blue
   [2,2] =  2
   [1,3] = Green
   [2,3] =  3
   [1,4] = Yellow
   [2,4] =  4
   [1,5] = White
   [2,5] =  5
}

Truy cập dữ liệu trong mảng ô

Có hai cách để tham chiếu đến các phần tử của một mảng ô:

• Bao quanh các chỉ số trong dấu ngoặc đơn đầu tiên (), để tham chiếu đến tập hợp các ô
• Bao quanh các chỉ số trong dấu ngoặc nhọn {}, để tham chiếu đến dữ liệu trong các ô riêng lẻ

Khi bạn đặt các chỉ số trong dấu ngoặc đơn đầu tiên, nó đề cập đến tập hợp các ô.

Chỉ số mảng ô trong dấu ngoặc đơn trơn tham chiếu đến tập hợp các ô.

Ví dụ -

c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c(1:2,1:2)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans = 
{
   [1,1] = Red
   [2,1] =  1
   [1,2] = Blue
   [2,2] =  2
}

Bạn cũng có thể truy cập nội dung của các ô bằng cách lập chỉ mục với dấu ngoặc nhọn.

Ví dụ -

c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c{1, 2:4}

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans = Blue
ans = Green
ans = Yellow

Các colon(:)là một trong những toán tử hữu ích nhất trong MATLAB. Nó được sử dụng để tạo vectơ, mảng chỉ số con vàspecify for iterations.

Nếu bạn muốn tạo một vectơ hàng, chứa các số nguyên từ 1 đến 10, bạn viết:

1:10

MATLAB thực hiện câu lệnh và trả về một vectơ hàng chứa các số nguyên từ 1 đến 10 -

ans =                                                                           
                                                                                
   1    2    3    4    5    6    7    8    9   10

Nếu bạn muốn chỉ định một giá trị gia tăng khác với một, ví dụ:

100: -5: 50

MATLAB thực hiện câu lệnh và trả về kết quả sau:

ans =
   100    95    90    85    80    75    70    65    60    55    50

Hãy để chúng tôi lấy một ví dụ khác -

0:pi/8:pi

MATLAB thực hiện câu lệnh và trả về kết quả sau:

ans =
   Columns 1 through 7
      0    0.3927    0.7854    1.1781    1.5708    1.9635    2.3562
   Columns 8 through 9
      2.7489    3.1416

Bạn có thể sử dụng toán tử dấu hai chấm để tạo vectơ chỉ số để chọn hàng, cột hoặc phần tử của mảng.

Bảng sau đây mô tả việc sử dụng nó cho mục đích này (cho chúng ta một ma trận A) -

định dạng	Mục đích
A(:,j)	là cột thứ j của A.
A(i,:)	là hàng thứ i của A.
A(:,:)	là mảng hai chiều tương đương. Đối với ma trận, điều này giống như A.
A(j:k)	là A (j), A (j + 1), ..., A (k).
A(:,j:k)	là A (:, j), A (:, j + 1), ..., A (:, k).
A(:,:,k)	là trang thứ k của mảng A ba chiều.
A(i,j,k,:)	là một vectơ trong mảng bốn chiều A. Vectơ bao gồm A (i, j, k, 1), A (i, j, k, 2), A (i, j, k, 3), v.v.
A(:)	là tất cả các phần tử của A, được coi là một cột duy nhất. Ở bên trái của một câu lệnh gán, A (:) điền vào A, giữ nguyên hình dạng của nó từ trước đó. Trong trường hợp này, vế phải chứa cùng số phần tử với A.

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

A = [1 2 3 4; 4 5 6 7; 7 8 9 10]
A(:,2)      % second column of A
A(:,2:3)    % second and third column of A
A(2:3,2:3)  % second and third rows and second and third columns

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

A =
      1     2     3     4
      4     5     6     7
      7     8     9    10

ans =
      2
      5
      8

ans =
      2     3
      5     6
      8     9

ans =
      5     6
      8     9

MATLAB hỗ trợ các lớp số khác nhau bao gồm các số nguyên có dấu và không dấu và các số dấu phẩy động chính xác đơn và chính xác kép. Theo mặc định, MATLAB lưu trữ tất cả các giá trị số dưới dạng số dấu phẩy động có độ chính xác kép.

Bạn có thể chọn lưu trữ bất kỳ số hoặc mảng số nào dưới dạng số nguyên hoặc số chính xác đơn.

Tất cả các kiểu số đều hỗ trợ các phép toán mảng và phép toán cơ bản.

Chuyển đổi sang các loại dữ liệu số khác nhau

MATLAB cung cấp các hàm sau để chuyển đổi sang các kiểu dữ liệu số khác nhau:

Chức năng	Mục đích
gấp đôi	Chuyển đổi thành số chính xác gấp đôi
Độc thân	Chuyển đổi thành số chính xác duy nhất
int8	Chuyển đổi thành số nguyên có dấu 8 bit
int16	Chuyển đổi thành số nguyên có dấu 16 bit
int32	Chuyển đổi thành số nguyên có dấu 32 bit
int64	Chuyển đổi thành số nguyên có dấu 64 bit
uint8	Chuyển đổi thành số nguyên không dấu 8 bit
uint16	Chuyển đổi thành số nguyên không dấu 16 bit
uint32	Chuyển đổi thành số nguyên không dấu 32 bit
uint64	Chuyển đổi thành số nguyên không dấu 64 bit

Thí dụ

Tạo một tệp kịch bản và nhập mã sau:

x = single([5.32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5

Khi bạn chạy tệp, nó hiển thị kết quả sau:

x =

   39.900   26.025   47.100

x =

   39.900   26.025   47.100

x =

   38  23  45

x =

   38  23  45

x =

   38  23  45

x =

   38  23  45

Thí dụ

Hãy để chúng tôi mở rộng ví dụ trước hơn một chút. Tạo một tệp kịch bản và nhập mã sau:

x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
x = num2cell(x)

Khi bạn chạy tệp, nó hiển thị kết quả sau:

x =

   38  23  45

x =

   38  23  45

x = 
{
   [1,1] = 38
   [1,2] = 23
   [1,3] = 45
}

Số nguyên nhỏ nhất và lớn nhất

Chức năng intmax() và intmin() trả về giá trị lớn nhất và nhỏ nhất có thể được biểu diễn với tất cả các loại số nguyên.

Cả hai hàm đều lấy kiểu dữ liệu số nguyên làm đối số, ví dụ, intmax (int8) hoặc intmin (int64) và trả về giá trị lớn nhất và nhỏ nhất mà bạn có thể đại diện cho kiểu dữ liệu số nguyên.

Thí dụ

Ví dụ sau minh họa cách lấy giá trị nhỏ nhất và lớn nhất của số nguyên. Tạo một tệp script và viết đoạn mã sau vào đó:

% displaying the smallest and largest signed integer data
str = 'The range for int8 is:\n\t%d to %d ';
sprintf(str, intmin('int8'), intmax('int8'))
str = 'The range for int16 is:\n\t%d to %d ';
sprintf(str, intmin('int16'), intmax('int16'))
str = 'The range for int32 is:\n\t%d to %d ';
sprintf(str, intmin('int32'), intmax('int32'))
str = 'The range for int64 is:\n\t%d to %d ';
sprintf(str, intmin('int64'), intmax('int64'))
 
% displaying the smallest and largest unsigned integer data
str = 'The range for uint8 is:\n\t%d to %d ';
sprintf(str, intmin('uint8'), intmax('uint8'))
str = 'The range for uint16 is:\n\t%d to %d ';
sprintf(str, intmin('uint16'), intmax('uint16'))
str = 'The range for uint32 is:\n\t%d to %d ';
sprintf(str, intmin('uint32'), intmax('uint32'))
str = 'The range for uint64 is:\n\t%d to %d ';
sprintf(str, intmin('uint64'), intmax('uint64'))

Khi bạn chạy tệp, nó hiển thị kết quả sau:

ans = The range for int8 is:
	-128 to 127 
ans = The range for int16 is:
	-32768 to 32767 
ans = The range for int32 is:
	-2147483648 to 2147483647 
ans = The range for int64 is:
	0 to 0 
ans = The range for uint8 is:
	0 to 255 
ans = The range for uint16 is:
	0 to 65535 
ans = The range for uint32 is:
	0 to -1 
ans = The range for uint64 is:
	0 to 18446744073709551616

Số dấu chấm động nhỏ nhất và lớn nhất

Chức năng realmax() và realmin() trả về giá trị lớn nhất và giá trị nhỏ nhất có thể được biểu diễn bằng số dấu phẩy động.

Cả hai hàm khi được gọi với đối số 'single', trả về giá trị lớn nhất và nhỏ nhất mà bạn có thể biểu diễn với kiểu dữ liệu độ chính xác đơn và khi được gọi với đối số 'double', trả về giá trị lớn nhất và nhỏ nhất mà bạn có thể đại diện kiểu dữ liệu độ chính xác kép.

Thí dụ

Ví dụ sau minh họa cách lấy số dấu phẩy động nhỏ nhất và lớn nhất. Tạo một tệp script và viết đoạn mã sau vào đó:

% displaying the smallest and largest single-precision 
% floating point number
str = 'The range for single is:\n\t%g to %g and\n\t %g to  %g';
sprintf(str, -realmax('single'), -realmin('single'), ...
   realmin('single'), realmax('single'))

% displaying the smallest and largest double-precision 
% floating point number
str = 'The range for double is:\n\t%g to %g and\n\t %g to  %g';
sprintf(str, -realmax('double'), -realmin('double'), ...
   realmin('double'), realmax('double'))

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans = The range for single is:                                                  
        -3.40282e+38 to -1.17549e-38 and                                        
         1.17549e-38 to  3.40282e+38                                            
ans = The range for double is:                                                  
        -1.79769e+308 to -2.22507e-308 and                                      
         2.22507e-308 to  1.79769e+308

Tạo một chuỗi ký tự khá đơn giản trong MATLAB. Trong thực tế, chúng tôi đã sử dụng nó nhiều lần. Ví dụ: bạn nhập dòng sau vào dấu nhắc lệnh:

my_string = 'Tutorials Point'

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

my_string = Tutorials Point

MATLAB coi tất cả các biến là mảng và chuỗi được coi là mảng ký tự. Hãy để chúng tôi sử dụngwhos lệnh để kiểm tra biến được tạo ở trên -

whos

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

Name           Size            Bytes  Class    Attributes
my_string      1x16               32  char

Điều thú vị là bạn có thể sử dụng các hàm chuyển đổi số như uint8 hoặc là uint16để chuyển đổi các ký tự trong chuỗi thành mã số của chúng. Cácchar hàm chuyển đổi vectơ số nguyên trở lại các ký tự -

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

my_string = 'Tutorial''s Point';
str_ascii = uint8(my_string)        % 8-bit ascii values
str_back_to_char= char(str_ascii)  
str_16bit = uint16(my_string)       % 16-bit ascii values
str_back_to_char = char(str_16bit)

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

str_ascii =

   84  117  116  111  114  105   97  108   39  115   32   80  111  105  110  116

str_back_to_char = Tutorial's Point
str_16bit =

   84  117  116  111  114  105   97  108   39  115   32   80  111  105  110  116

str_back_to_char = Tutorial's Point

Mảng ký tự hình chữ nhật

Các chuỗi mà chúng ta đã thảo luận cho đến nay là các mảng ký tự một chiều; tuy nhiên, chúng ta cần lưu trữ nhiều hơn thế. Chúng ta cần lưu trữ nhiều dữ liệu dạng văn bản hơn trong chương trình của mình. Điều này đạt được bằng cách tạo các mảng ký tự hình chữ nhật.

Cách đơn giản nhất để tạo mảng ký tự hình chữ nhật là nối hai hoặc nhiều mảng ký tự một chiều, theo chiều dọc hoặc chiều ngang theo yêu cầu.

Bạn có thể kết hợp các chuỗi theo chiều dọc theo một trong các cách sau:

• Sử dụng toán tử nối MATLAB []và ngăn cách mỗi hàng bằng dấu chấm phẩy (;). Xin lưu ý rằng trong phương pháp này mỗi hàng phải chứa cùng một số ký tự. Đối với các chuỗi có độ dài khác nhau, bạn nên đệm các ký tự khoảng trắng nếu cần.

• Sử dụng charchức năng. Nếu các chuỗi có độ dài khác nhau, ký tự đệm các chuỗi ngắn hơn bằng khoảng trống ở cuối để mỗi hàng có cùng số ký tự.

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

doc_profile = ['Zara Ali                             '; ...
               'Sr. Surgeon                          '; ...
               'R N Tagore Cardiology Research Center']
doc_profile = char('Zara Ali', 'Sr. Surgeon', ...
                  'RN Tagore Cardiology Research Center')

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

doc_profile =
Zara Ali                             
Sr. Surgeon                          
R N Tagore Cardiology Research Center
doc_profile =
Zara Ali                            
Sr. Surgeon                         
RN Tagore Cardiology Research Center

Bạn có thể kết hợp các chuỗi theo chiều ngang theo một trong các cách sau:

• Sử dụng toán tử nối MATLAB, []và phân tách các chuỗi đầu vào bằng dấu phẩy hoặc dấu cách. Phương thức này bảo toàn bất kỳ khoảng trống nào trong các mảng đầu vào.

• Sử dụng hàm nối chuỗi, strcat. Phương pháp này loại bỏ khoảng trống ở cuối trong các đầu vào.

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

name =     'Zara Ali                             ';
position = 'Sr. Surgeon                          '; 
worksAt =  'R N Tagore Cardiology Research Center';
profile = [name ', ' position ', ' worksAt]
profile = strcat(name, ', ', position, ', ', worksAt)

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

profile = Zara Ali      , Sr. Surgeon      , R N Tagore Cardiology Research Center
profile = Zara Ali,Sr. Surgeon,R N Tagore Cardiology Research Center

Kết hợp các chuỗi thành một mảng ô

Từ cuộc thảo luận trước đây của chúng tôi, rõ ràng là việc kết hợp các chuỗi có độ dài khác nhau có thể là một vấn đề khó khăn vì tất cả các chuỗi trong mảng phải có cùng độ dài. Chúng tôi đã sử dụng khoảng trắng ở cuối các chuỗi để cân bằng độ dài của chúng.

Tuy nhiên, một cách hiệu quả hơn để kết hợp các chuỗi là chuyển đổi mảng kết quả thành một mảng ô.

Mảng ô MATLAB có thể chứa các kích thước và kiểu dữ liệu khác nhau trong một mảng. Mảng ô cung cấp một cách linh hoạt hơn để lưu trữ các chuỗi có độ dài khác nhau.

Các cellstr hàm chuyển đổi một mảng ký tự thành một mảng ô chuỗi.

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

name =     'Zara Ali                             ';
position = 'Sr. Surgeon                          '; 
worksAt =  'R N Tagore Cardiology Research Center';
profile = char(name, position, worksAt);
profile = cellstr(profile);
disp(profile)

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

{                                                                               
   [1,1] = Zara Ali                                                              
   [2,1] = Sr. Surgeon                                                           
   [3,1] = R N Tagore Cardiology Research Center                                 
}

Các hàm chuỗi trong MATLAB

MATLAB cung cấp nhiều hàm chuỗi tạo, kết hợp, phân tích cú pháp, so sánh và thao tác các chuỗi.

Bảng sau cung cấp mô tả ngắn gọn về các hàm chuỗi trong MATLAB:

Chức năng	Purpose
Functions for storing text in character arrays, combine character arrays, etc.
blanks	Create string of blank characters
cellstr	Create cell array of strings from character array
char	Convert to character array (string)
iscellstr	Determine whether input is cell array of strings
ischar	Determine whether item is character array
sprintf	Format data into string
strcat	Concatenate strings horizontally
strjoin	Join strings in cell array into single string
Functions for identifying parts of strings, find and replace substrings
ischar	Determine whether item is character array
isletter	Array elements that are alphabetic letters
isspace	Array elements that are space characters
isstrprop	Determine whether string is of specified category
sscanf	Read formatted data from string
strfind	Find one string within another
strrep	Find and replace substring
strsplit	Split string at specified delimiter
strtok	Selected parts of string
validatestring	Check validity of text string
symvar	Determine symbolic variables in expression
regexp	Match regular expression (case sensitive)
regexpi	Match regular expression (case insensitive)
regexprep	Replace string using regular expression
regexptranslate	Translate string into regular expression
Functions for string comparison
strcmp	Compare strings (case sensitive)
strcmpi	Compare strings (case insensitive)
strncmp	Compare first n characters of strings (case sensitive)
strncmpi	Compare first n characters of strings (case insensitive)
Functions for changing string to upper- or lowercase, creating or removing white space
deblank	Strip trailing blanks from end of string
strtrim	Remove leading and trailing white space from string
lower	Convert string to lowercase
upper	Convert string to uppercase
strjust	Justify character array

Examples

The following examples illustrate some of the above-mentioned string functions −

Formatting Strings

Create a script file and type the following code into it −

A = pi*1000*ones(1,5);
sprintf(' %f \n %.2f \n %+.2f \n %12.2f \n %012.2f \n', A)

When you run the file, it displays the following result −

ans =  3141.592654 
   3141.59 
   +3141.59 
      3141.59 
   000003141.59

Joining Strings

Create a script file and type the following code into it −

%cell array of strings
str_array = {'red','blue','green', 'yellow', 'orange'};

% Join strings in cell array into single string
str1 = strjoin(str_array, "-")
str2 = strjoin(str_array, ",")

When you run the file, it displays the following result −

str1 = red-blue-green-yellow-orange
str2 = red,blue,green,yellow,orange

Finding and Replacing Strings

Create a script file and type the following code into it −

students = {'Zara Ali', 'Neha Bhatnagar', ...
            'Monica Malik', 'Madhu Gautam', ...
            'Madhu Sharma', 'Bhawna Sharma',...
            'Nuha Ali', 'Reva Dutta', ...
            'Sunaina Ali', 'Sofia Kabir'};
 
% The strrep function searches and replaces sub-string.
new_student = strrep(students(8), 'Reva', 'Poulomi')
% Display first names
first_names = strtok(students)

When you run the file, it displays the following result −

new_student = 
{
   [1,1] = Poulomi Dutta
}
first_names = 
{
   [1,1] = Zara
   [1,2] = Neha
   [1,3] = Monica
   [1,4] = Madhu
   [1,5] = Madhu
   [1,6] = Bhawna
   [1,7] = Nuha
   [1,8] = Reva
   [1,9] = Sunaina
   [1,10] = Sofia
}

Comparing Strings

Create a script file and type the following code into it −

str1 = 'This is test'
str2 = 'This is text'
if (strcmp(str1, str2))
   sprintf('%s and %s are equal', str1, str2)
else
   sprintf('%s and %s are not equal', str1, str2)
end

When you run the file, it displays the following result −

str1 = This is test
str2 = This is text
ans = This is test and This is text are not equal

A function is a group of statements that together perform a task. In MATLAB, functions are defined in separate files. The name of the file and of the function should be the same.

Functions operate on variables within their own workspace, which is also called the local workspace, separate from the workspace you access at the MATLAB command prompt which is called the base workspace.

Functions can accept more than one input arguments and may return more than one output arguments.

Syntax of a function statement is −

function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)

Example

The following function named mymax should be written in a file named mymax.m. It takes five numbers as argument and returns the maximum of the numbers.

Create a function file, named mymax.m and type the following code in it −

function max = mymax(n1, n2, n3, n4, n5)

%This function calculates the maximum of the
% five numbers given as input
max =  n1;
if(n2 > max)
   max = n2;
end
if(n3 > max)
   max = n3;
end
if(n4 > max)
   max = n4;
end
if(n5 > max)
   max = n5;
end

The first line of a function starts with the keyword function. It gives the name of the function and order of arguments. In our example, the mymax function has five input arguments and one output argument.

The comment lines that come right after the function statement provide the help text. These lines are printed when you type −

help mymax

MATLAB will execute the above statement and return the following result −

This function calculates the maximum of the
   five numbers given as input

You can call the function as −

mymax(34, 78, 89, 23, 11)

MATLAB will execute the above statement and return the following result −

ans = 89

Anonymous Functions

An anonymous function is like an inline function in traditional programming languages, defined within a single MATLAB statement. It consists of a single MATLAB expression and any number of input and output arguments.

You can define an anonymous function right at the MATLAB command line or within a function or script.

This way you can create simple functions without having to create a file for them.

The syntax for creating an anonymous function from an expression is

f = @(arglist)expression

Example

In this example, we will write an anonymous function named power, which will take two numbers as input and return first number raised to the power of the second number.

Create a script file and type the following code in it −

power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)

When you run the file, it displays −

result1 =  343
result2 =  7
result3 =  1.0000e-10
result4 =  9.5459

Primary and Sub-Functions

Any function other than an anonymous function must be defined within a file. Each function file contains a required primary function that appears first and any number of optional sub-functions that comes after the primary function and used by it.

Primary functions can be called from outside of the file that defines them, either from command line or from other functions, but sub-functions cannot be called from command line or other functions, outside the function file.

Sub-functions are visible only to the primary function and other sub-functions within the function file that defines them.

Example

Let us write a function named quadratic that would calculate the roots of a quadratic equation. The function would take three inputs, the quadratic co-efficient, the linear co-efficient and the constant term. It would return the roots.

The function file quadratic.m will contain the primary function quadratic and the sub-function disc, which calculates the discriminant.

Create a function file quadratic.m and type the following code in it −

function [x1,x2] = quadratic(a,b,c)

%this function returns the roots of 
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficients of x2, x and the 
%constant term
% It returns the roots
d = disc(a,b,c); 
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end   % end of quadratic

function dis = disc(a,b,c) 
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end   % end of sub-function

You can call the above function from command prompt as −

quadratic(2,4,-4)

MATLAB will execute the above statement and return the following result −

ans = 0.7321

Nested Functions

You can define functions within the body of another function. These are called nested functions. A nested function contains any or all of the components of any other function.

Nested functions are defined within the scope of another function and they share access to the containing function's workspace.

A nested function follows the following syntax −

function x = A(p1, p2)
...
B(p2)
   function y = B(p3)
   ...
   end
...
end

Example

Let us rewrite the function quadratic, from previous example, however, this time the disc function will be a nested function.

Create a function file quadratic2.m and type the following code in it −

function [x1,x2] = quadratic2(a,b,c)
function disc  % nested function
d = sqrt(b^2 - 4*a*c);
end   % end of function disc

disc;
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end   % end of function quadratic2

You can call the above function from command prompt as −

quadratic2(2,4,-4)

MATLAB will execute the above statement and return the following result −

ans =  0.73205

Private Functions

A private function is a primary function that is visible only to a limited group of other functions. If you do not want to expose the implementation of a function(s), you can create them as private functions.

Private functions reside in subfolders with the special name private.

They are visible only to functions in the parent folder.

Example

Let us rewrite the quadratic function. This time, however, the disc function calculating the discriminant, will be a private function.

Create a subfolder named private in working directory. Store the following function file disc.m in it −

function dis = disc(a,b,c) 
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end      % end of sub-function

Create a function quadratic3.m in your working directory and type the following code in it −

function [x1,x2] = quadratic3(a,b,c)

%this function returns the roots of 
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficient of x2, x and the 
%constant term
% It returns the roots
d = disc(a,b,c); 

x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end      % end of quadratic3

You can call the above function from command prompt as −

quadratic3(2,4,-4)

MATLAB will execute the above statement and return the following result −

ans =  0.73205

Global Variables

Global variables can be shared by more than one function. For this, you need to declare the variable as global in all the functions.

If you want to access that variable from the base workspace, then declare the variable at the command line.

The global declaration must occur before the variable is actually used in a function. It is a good practice to use capital letters for the names of global variables to distinguish them from other variables.

Example

Let us create a function file named average.m and type the following code in it −

function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
end

Create a script file and type the following code in it −

global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)

When you run the file, it will display the following result −

av =  35.500

Importing data in MATLAB means loading data from an external file. The importdata function allows loading various data files of different formats. It has the following five forms −

Sr.No.	Function & Description
1	A = importdata(filename) Loads data into array A from the file denoted by filename.
2	A = importdata('-pastespecial') Loads data from the system clipboard rather than from a file.
3	A = importdata(___, delimiterIn) Interprets delimiterIn as the column separator in ASCII file, filename, or the clipboard data. You can use delimiterIn with any of the input arguments in the above syntaxes.
4	A = importdata(___, delimiterIn, headerlinesIn) Loads data from ASCII file, filename, or the clipboard, reading numeric data starting from line headerlinesIn+1.
5	[A, delimiterOut, headerlinesOut] = importdata(___) Returns the detected delimiter character for the input ASCII file in delimiterOut and the detected number of header lines in headerlinesOut, using any of the input arguments in the previous syntaxes.

By default, Octave does not have support for importdata() function, so you will have to search and install this package to make following examples work with your Octave installation.

Example 1

Let us load and display an image file. Create a script file and type the following code in it −

filename = 'smile.jpg';
A = importdata(filename);
image(A);

When you run the file, MATLAB displays the image file. However, you must store it in the current directory.

Example 2

In this example, we import a text file and specify Delimiter and Column Header. Let us create a space-delimited ASCII file with column headers, named weeklydata.txt.

Our text file weeklydata.txt looks like this −

SunDay  MonDay  TuesDay  WednesDay  ThursDay  FriDay  SaturDay
95.01   76.21   61.54    40.57       55.79    70.28   81.53
73.11   45.65   79.19    93.55       75.29    69.87   74.68
60.68   41.85   92.18    91.69       81.32    90.38   74.51
48.60   82.14   73.82    41.03       0.99     67.22   93.18
89.13   44.47   57.63    89.36       13.89    19.88   46.60

Create a script file and type the following code in it −

filename = 'weeklydata.txt';
delimiterIn = ' ';
headerlinesIn = 1;
A = importdata(filename,delimiterIn,headerlinesIn);

% View data
for k = [1:7]
   disp(A.colheaders{1, k})
   disp(A.data(:, k))
   disp(' ')
end

When you run the file, it displays the following result −

SunDay
   95.0100
   73.1100
   60.6800
   48.6000
   89.1300
 
MonDay
   76.2100
   45.6500
   41.8500
   82.1400
   44.4700
 
TuesDay
   61.5400
   79.1900
   92.1800
   73.8200
   57.6300

WednesDay
   40.5700
   93.5500
   91.6900
   41.0300
   89.3600
 
ThursDay
   55.7900
   75.2900
   81.3200
   0.9900
   13.8900
 
FriDay
   70.2800
   69.8700
   90.3800
   67.2200
   19.8800

SaturDay
   81.5300
   74.6800
   74.5100
   93.1800
   46.6000

Ví dụ 3

Trong ví dụ này, hãy để chúng tôi nhập dữ liệu từ khay nhớ tạm.

Sao chép các dòng sau vào khay nhớ tạm -

Mathematics is simple

Tạo một tệp kịch bản và nhập mã sau:

A = importdata('-pastespecial')

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

A = 
   'Mathematics is simple'

I / O Tệp Cấp thấp

Hàm importdata là một hàm cấp cao. Các chức năng I / O tệp cấp thấp trong MATLAB cho phép kiểm soát nhiều nhất việc đọc hoặc ghi dữ liệu vào tệp. Tuy nhiên, các chức năng này cần thêm thông tin chi tiết về tệp của bạn để hoạt động hiệu quả.

MATLAB cung cấp các hàm sau cho các hoạt động đọc và ghi ở cấp độ byte hoặc ký tự:

Chức năng	Sự miêu tả
fclose	Đóng một hoặc tất cả các tệp đang mở
giả vờ	Kiểm tra phần cuối của tệp
niềm đam mê	Thông tin về lỗi I / O tệp
fgetl	Đọc dòng từ tệp, xóa các ký tự dòng mới
đồ ăn vặt	Đọc dòng từ tệp, giữ các ký tự dòng mới
fopen	Mở tệp hoặc lấy thông tin về các tệp đang mở
fprintf	Ghi dữ liệu vào tệp văn bản
bánh mì	Đọc dữ liệu từ tệp nhị phân
tự do	Di chuyển chỉ báo vị trí tệp đến đầu tệp đang mở
fscanf	Đọc dữ liệu từ tệp văn bản
fseek	Di chuyển đến vị trí được chỉ định trong tệp
ftell	Vị trí trong tệp đang mở
fwrite	Ghi dữ liệu vào tệp nhị phân

Nhập tệp dữ liệu văn bản với I / O cấp thấp

MATLAB cung cấp các chức năng sau để nhập các tệp dữ liệu văn bản ở mức độ thấp:

• Các fscanf chức năng đọc dữ liệu được định dạng trong một văn bản hoặc tệp ASCII.

• Các fgetl và fgets các hàm đọc một dòng của tệp tại một thời điểm, trong đó một ký tự dòng mới phân tách mỗi dòng.

• Các fread hàm đọc một luồng dữ liệu ở mức byte hoặc bit.

Thí dụ

Chúng tôi có một tệp dữ liệu văn bản 'myfile.txt' được lưu trong thư mục làm việc của chúng tôi. Tệp lưu trữ dữ liệu lượng mưa trong ba tháng; Tháng 6, tháng 7 và tháng 8 trong năm 2012.

Dữ liệu trong myfile.txt chứa các bộ đo thời gian, tháng và lượng mưa lặp lại ở năm địa điểm. Dữ liệu tiêu đề lưu trữ số tháng M; vì vậy ta có M tập hợp các số đo.

Tệp trông như thế này -

Rainfall Data
Months: June, July, August
 
M = 3
12:00:00
June-2012
17.21  28.52  39.78  16.55 23.67
19.15  0.35   17.57  NaN   12.01
17.92  28.49  17.40  17.06 11.09
9.59   9.33   NaN    0.31  0.23 
10.46  13.17  NaN    14.89 19.33
20.97  19.50  17.65  14.45 14.00
18.23  10.34  17.95  16.46 19.34
09:10:02
July-2012
12.76  16.94  14.38  11.86 16.89
20.46  23.17  NaN    24.89 19.33
30.97  49.50  47.65  24.45 34.00
18.23  30.34  27.95  16.46 19.34
30.46  33.17  NaN    34.89  29.33
30.97  49.50  47.65  24.45 34.00
28.67  30.34  27.95  36.46 29.34
15:03:40
August-2012
17.09  16.55  19.59  17.25 19.22
17.54  11.45  13.48  22.55 24.01
NaN    21.19  25.85  25.05 27.21
26.79  24.98  12.23  16.99 18.67
17.54  11.45  13.48  22.55 24.01
NaN    21.19  25.85  25.05 27.21
26.79  24.98  12.23  16.99 18.67

Chúng tôi sẽ nhập dữ liệu từ tệp này và hiển thị dữ liệu này. Thực hiện các bước sau:

• Mở tệp bằng fopen và lấy mã định danh tệp.

• Mô tả dữ liệu trong tệp với format specifiers, nhu la '%s'cho một chuỗi,'%d'cho một số nguyên hoặc'%f'cho một số dấu phẩy động.

• Để bỏ qua các ký tự chữ trong tệp, hãy đưa chúng vào mô tả định dạng. Để bỏ qua trường dữ liệu, hãy sử dụng dấu hoa thị ('*') trong mã xác định.

  Ví dụ, để đọc tiêu đề và trả về giá trị duy nhất cho M, chúng ta viết:

  M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);

• Theo mặc định, fscanfđọc dữ liệu theo mô tả định dạng của chúng tôi cho đến khi nó không tìm thấy bất kỳ kết quả phù hợp nào với dữ liệu hoặc đến cuối tệp. Ở đây chúng ta sẽ sử dụng vòng lặp for để đọc 3 tập dữ liệu và mỗi lần, nó sẽ đọc 7 hàng và 5 cột.

• Chúng tôi sẽ tạo một cấu trúc có tên mydata trong vùng làm việc để lưu trữ dữ liệu đọc được từ tệp. Cấu trúc này có ba trường - thời gian , tháng và mảng dữ liệu mưa .

Tạo một tệp script và nhập mã sau vào đó:

filename = '/data/myfile.txt';
rows = 7;
cols = 5;
 
% open the file
fid = fopen(filename);
 
% read the file headers, find M (number of months)
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);
 
% read each set of measurements
for n = 1:M
   mydata(n).time = fscanf(fid, '%s', 1);
   mydata(n).month = fscanf(fid, '%s', 1);
 
   % fscanf fills the array in column order,
   % so transpose the results
   mydata(n).raindata  = ...
      fscanf(fid, '%f', [rows, cols]);
end
for n = 1:M
   disp(mydata(n).time), disp(mydata(n).month)
   disp(mydata(n).raindata)
end
 
% close the file
fclose(fid);

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

12:00:00
June-2012
   17.2100   17.5700   11.0900   13.1700   14.4500
   28.5200       NaN    9.5900       NaN   14.0000
   39.7800   12.0100    9.3300   14.8900   18.2300
   16.5500   17.9200       NaN   19.3300   10.3400
   23.6700   28.4900    0.3100   20.9700   17.9500
   19.1500   17.4000    0.2300   19.5000   16.4600
   0.3500   17.0600   10.4600   17.6500   19.3400

09:10:02
July-2012
   12.7600       NaN   34.0000   33.1700   24.4500
   16.9400   24.8900   18.2300       NaN   34.0000
   14.3800   19.3300   30.3400   34.8900   28.6700
   11.8600   30.9700   27.9500   29.3300   30.3400
   16.8900   49.5000   16.4600   30.9700   27.9500
   20.4600   47.6500   19.3400   49.5000   36.4600
   23.1700   24.4500   30.4600   47.6500   29.3400

15:03:40
August-2012
   17.0900   13.4800   27.2100   11.4500   25.0500
   16.5500   22.5500   26.7900   13.4800   27.2100
   19.5900   24.0100   24.9800   22.5500   26.7900
   17.2500       NaN   12.2300   24.0100   24.9800
   19.2200   21.1900   16.9900       NaN   12.2300
   17.5400   25.8500   18.6700   21.1900   16.9900
   11.4500   25.0500   17.5400   25.8500   18.6700

Xuất (hoặc xuất) dữ liệu trong MATLAB có nghĩa là ghi vào tệp. MATLAB cho phép bạn sử dụng dữ liệu của mình trong một ứng dụng khác có chức năng đọc các tệp ASCII. Đối với điều này, MATLAB cung cấp một số tùy chọn xuất dữ liệu.

Bạn có thể tạo các loại tệp sau:

• Tệp dữ liệu ASCII hình chữ nhật, được phân tách từ một mảng.

• Tệp nhật ký (hoặc nhật ký) của các lần gõ phím và kết quả đầu ra văn bản.

• Tệp ASCII chuyên biệt sử dụng các hàm cấp thấp như fprintf.

• MEX-file để truy cập quy trình C / C ++ hoặc Fortran của bạn để ghi vào một định dạng tệp văn bản cụ thể.

Ngoài ra, bạn cũng có thể xuất dữ liệu sang bảng tính.

Có hai cách để xuất một mảng số dưới dạng tệp dữ liệu ASCII được phân tách -

• Sử dụng save chức năng và chỉ định -ascii vòng loại

• Sử dụng dlmwrite chức năng

Cú pháp để sử dụng hàm lưu là:

save my_data.out num_array -ascii

trong đó, my_data.out là tệp dữ liệu ASCII được phân tách được tạo, num_array là một mảng số và−ascii là định nghĩa.

Cú pháp để sử dụng dlmwrite chức năng là -

dlmwrite('my_data.out', num_array, 'dlm_char')

trong đó, my_data.out là tệp dữ liệu ASCII được phân tách được tạo, num_array là một mảng số và dlm_char là ký tự phân tách.

Thí dụ

Ví dụ sau đây minh họa khái niệm. Tạo một tệp kịch bản và nhập mã sau:

num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ascii;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.out

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

1.0000000e+00   2.0000000e+00   3.0000000e+00   4.0000000e+00
   4.0000000e+00   5.0000000e+00   6.0000000e+00   7.0000000e+00
   7.0000000e+00   8.0000000e+00   9.0000000e+00   0.0000000e+00

1 2 3 4
4 5 6 7
7 8 9 0

Xin lưu ý rằng lệnh save -ascii và hàm dlmwrite không hoạt động với mảng ô làm đầu vào. Để tạo tệp ASCII được phân tách từ nội dung của một mảng ô, bạn có thể

• Hoặc, chuyển đổi mảng ô thành ma trận bằng cách sử dụng cell2mat chức năng

• Hoặc xuất mảng ô bằng các hàm I / O tệp cấp thấp.

Nếu bạn sử dụng save hàm ghi một mảng ký tự vào tệp ASCII, nó ghi tương đương ASCII của các ký tự vào tệp.

Ví dụ: chúng ta hãy viết từ 'xin chào' vào một tệp -

h = 'hello';
save textdata.out h -ascii
type textdata.out

MATLAB thực hiện các câu lệnh trên và hiển thị kết quả sau. là các ký tự của chuỗi 'xin chào' ở định dạng ASCII 8 chữ số.

1.0400000e+02   1.0100000e+02   1.0800000e+02   1.0800000e+02   1.1100000e+02

Ghi vào tệp nhật ký

Tệp nhật ký là nhật ký hoạt động của phiên MATLAB của bạn. Chức năng nhật ký tạo một bản sao chính xác của phiên của bạn trong một tệp đĩa, không bao gồm đồ họa.

Để bật chức năng nhật ký, hãy nhập -

diary

Theo tùy chọn, bạn có thể đặt tên của tệp nhật ký, giả sử -

diary logdata.out

Để tắt chức năng nhật ký -

diary off

Bạn có thể mở tệp nhật ký trong trình soạn thảo văn bản.

Xuất dữ liệu sang tệp dữ liệu văn bản với I / O cấp thấp

Cho đến nay, chúng tôi đã xuất mảng số. Tuy nhiên, bạn có thể cần tạo các tệp văn bản khác, bao gồm kết hợp dữ liệu số và ký tự, tệp đầu ra không phải hình chữ nhật hoặc tệp có lược đồ mã hóa không phải ASCII. Đối với những mục đích này, MATLAB cung cấp mức thấpfprintf chức năng.

Như trong các hoạt động tệp I / O cấp thấp, trước khi xuất, bạn cần mở hoặc tạo tệp bằng fopenvà lấy mã định danh tệp. Theo mặc định, fopen mở một tệp để truy cập chỉ đọc. Bạn nên chỉ định quyền để viết hoặc nối thêm, chẳng hạn như 'w' hoặc 'a'.

Sau khi xử lý tệp, bạn cần đóng tệp bằng fclose(fid) chức năng.

Ví dụ sau thể hiện khái niệm -

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

% create a matrix y, with two rows
x = 0:10:100;
y = [x; log(x)];
 
% open a file for writing
fid = fopen('logtable.txt', 'w');
 
% Table Header
fprintf(fid, 'Log     Function\n\n');
 
% print values in column order
% two values appear on each row of the file
fprintf(fid, '%f    %f\n', y);
fclose(fid);

% display the file created
type logtable.txt

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

Log         Function

0.000000    -Inf
10.000000    2.302585
20.000000    2.995732
30.000000    3.401197
40.000000    3.688879
50.000000    3.912023
60.000000    4.094345
70.000000    4.248495
80.000000    4.382027
90.000000    4.499810
100.000000    4.605170

Để vẽ đồ thị của một hàm, bạn cần thực hiện các bước sau:

• Định nghĩa x, bằng cách chỉ định range of values cho biến x, mà hàm sẽ được vẽ

• Xác định chức năng, y = f(x)

• Gọi plot lệnh, như plot(x, y)

Ví dụ sau đây sẽ chứng minh khái niệm. Hãy để chúng tôi vẽ hàm đơn giảny = x cho phạm vi giá trị của x từ 0 đến 100, với số gia là 5.

Tạo một tệp kịch bản và nhập mã sau:

x = [0:5:100];
y = x;
plot(x, y)

Khi bạn chạy tệp, MATLAB hiển thị biểu đồ sau:

Chúng ta hãy lấy một ví dụ nữa để vẽ đồ thị của hàm y = x ² . Trong ví dụ này, chúng ta sẽ vẽ hai đồ thị với cùng một hàm, nhưng ở lần thứ hai, chúng ta sẽ giảm giá trị của gia số. Xin lưu ý rằng khi chúng tôi giảm số gia, biểu đồ sẽ trở nên mượt mà hơn.

Tạo một tệp kịch bản và nhập mã sau:

x = [1 2 3 4 5 6 7 8 9 10];
x = [-100:20:100];
y = x.^2;
plot(x, y)

Khi bạn chạy tệp, MATLAB hiển thị biểu đồ sau:

Thay đổi tệp mã một chút, giảm mức tăng xuống 5 -

x = [-100:5:100];
y = x.^2;
plot(x, y)

MATLAB vẽ một biểu đồ mượt mà hơn -

Thêm tiêu đề, nhãn, đường lưới và tỷ lệ trên biểu đồ

MATLAB cho phép bạn thêm tiêu đề, nhãn dọc theo trục x và trục y, đường lưới và cũng có thể điều chỉnh các trục để làm nổi bật biểu đồ.

• Các xlabel và ylabel lệnh tạo nhãn dọc theo trục x và trục y.

• Các title lệnh cho phép bạn đặt tiêu đề trên biểu đồ.

• Các grid on lệnh cho phép bạn đặt các đường lưới trên đồ thị.

• Các axis equal lệnh cho phép tạo ra cốt truyện với các hệ số tỷ lệ giống nhau và các khoảng trống trên cả hai trục.

• Các axis square lệnh tạo một ô vuông.

Thí dụ

Tạo một tệp kịch bản và nhập mã sau:

x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'),
grid on, axis equal

MATLAB tạo ra đồ thị sau:

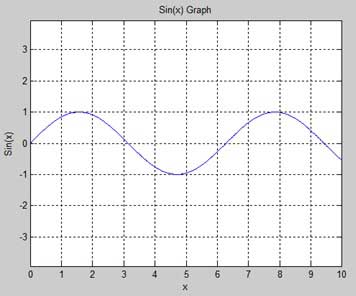
Vẽ nhiều hàm trên cùng một đồ thị

Bạn có thể vẽ nhiều đồ thị trên cùng một ô. Ví dụ sau thể hiện khái niệm -

Thí dụ

Tạo một tệp kịch bản và nhập mã sau:

x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')

MATLAB tạo ra đồ thị sau:

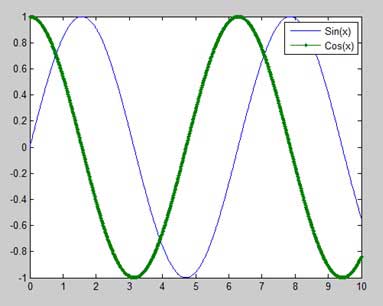
Đặt màu trên biểu đồ

MATLAB cung cấp tám tùy chọn màu cơ bản để vẽ đồ thị. Bảng sau đây cho thấy các màu và mã của chúng:

Mã	Màu sắc
w	trắng
k	Đen
b	Màu xanh da trời
r	Đỏ
c	Lục lam
g	màu xanh lá
m	Đỏ tươi
y	Màu vàng

Thí dụ

Hãy vẽ đồ thị của hai đa thức

• f (x) = 3x ⁴ + 2x ³ + 7x ² + 2x + 9 và

• g (x) = 5x ³ + 9x + 2

Tạo một tệp kịch bản và nhập mã sau:

x = [-10 : 0.01: 10];
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
plot(x, y, 'r', x, g, 'g')

Khi bạn chạy tệp, MATLAB tạo ra đồ thị sau:

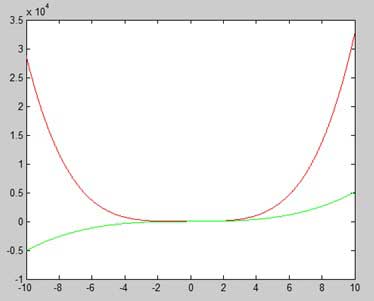
Thiết lập thang đo trục

Các axislệnh cho phép bạn thiết lập tỷ lệ trục. Bạn có thể cung cấp các giá trị tối thiểu và tối đa cho các trục x và y bằng lệnh axis theo cách sau:

axis ( [xmin xmax ymin ymax] )

Ví dụ sau đây cho thấy điều này -

Thí dụ

Tạo một tệp kịch bản và nhập mã sau:

x = [0 : 0.01: 10];
y = exp(-x).* sin(2*x + 3);
plot(x, y), axis([0 10 -1 1])

Khi bạn chạy tệp, MATLAB tạo ra đồ thị sau:

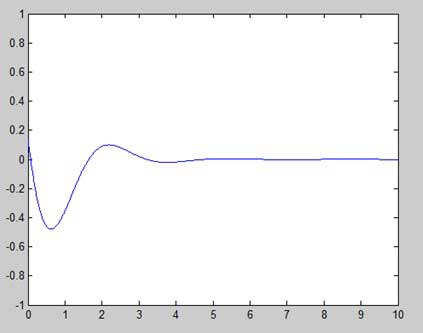
Tạo các lô phụ

Khi bạn tạo một mảng các ô trong cùng một hình, mỗi ô này được gọi là một ô con. Cácsubplot lệnh được sử dụng để tạo các ô con.

Cú pháp của lệnh là -

subplot(m, n, p)

trong đó, m và n là số hàng và cột của mảng ô và p chỉ định vị trí đặt một ô cụ thể.

Mỗi âm mưu được tạo bằng lệnh subplot có thể có các đặc điểm riêng. Ví dụ sau thể hiện khái niệm -

Thí dụ

Hãy để chúng tôi tạo ra hai âm mưu -

y = e ^−1,5x sin (10x)

y = e ^−2x sin (10x)

Tạo một tệp kịch bản và nhập mã sau:

x = [0:0.01:5];
y = exp(-1.5*x).*sin(10*x);
subplot(1,2,1)
plot(x,y), xlabel('x'),ylabel('exp(–1.5x)*sin(10x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(10*x);
subplot(1,2,2)
plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(10x)'),axis([0 5 -1 1])

Khi bạn chạy tệp, MATLAB tạo ra đồ thị sau:

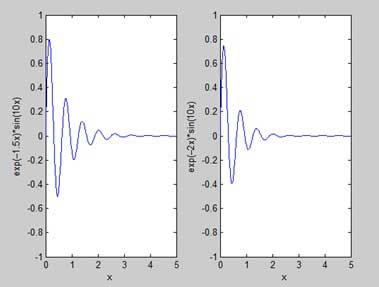
Chương này sẽ tiếp tục khám phá khả năng vẽ và đồ họa của MATLAB. Chúng ta sẽ thảo luận -

• Vẽ biểu đồ thanh
• Vẽ đường viền
• Lô ba chiều

Vẽ biểu đồ thanh

Các barlệnh vẽ biểu đồ thanh hai chiều. Hãy để chúng tôi lấy một ví dụ để chứng minh ý tưởng.

Thí dụ

Hãy để chúng tôi có một lớp học tưởng tượng với 10 học sinh. Chúng tôi biết phần trăm số điểm mà những học sinh này đạt được là 75, 58, 90, 87, 50, 85, 92, 75, 60 và 95. Chúng tôi sẽ vẽ biểu đồ thanh cho dữ liệu này.

Tạo một tệp kịch bản và nhập mã sau:

x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps

Khi bạn chạy tệp, MATLAB hiển thị biểu đồ thanh sau:

Vẽ đường viền

Đường đồng mức của một hàm hai biến là một đường cong mà hàm có giá trị không đổi. Đường đồng mức được sử dụng để tạo bản đồ đường đồng mức bằng cách nối các điểm có độ cao bằng nhau trên một mức nhất định, chẳng hạn như mực nước biển trung bình.

MATLAB cung cấp một contour chức năng vẽ bản đồ đường đồng mức.

Thí dụ

Hãy để chúng tôi tạo một bản đồ đường bao hiển thị các đường đồng mức cho một hàm đã cho g = f (x, y). Hàm này có hai biến. Vì vậy, chúng ta sẽ phải tạo ra hai biến độc lập, tức là hai tập dữ liệu x và y. Điều này được thực hiện bằng cách gọimeshgrid chỉ huy.

Các meshgrid lệnh được sử dụng để tạo ma trận các phần tử cung cấp phạm vi trên x và y cùng với đặc điểm kỹ thuật của gia số trong mỗi trường hợp.

Hãy vẽ đồ thị hàm g = f (x, y), trong đó −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Hãy để chúng tôi lấy gia số 0,1 cho cả hai giá trị. Các biến được đặt là -

[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);

Cuối cùng, chúng ta cần gán hàm. Cho hàm số của chúng ta là: x ² + y ²

Tạo một tệp kịch bản và nhập mã sau:

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
contour(x,y,g)                         % call the contour function
print -deps graph.eps

Khi bạn chạy tệp, MATLAB hiển thị bản đồ đường bao sau:

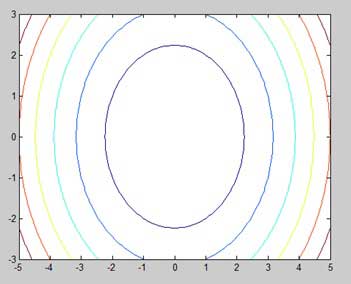
Hãy để chúng tôi sửa đổi mã một chút để chỉnh sửa bản đồ

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
[C, h] = contour(x,y,g);               % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.eps

Khi bạn chạy tệp, MATLAB hiển thị bản đồ đường bao sau:

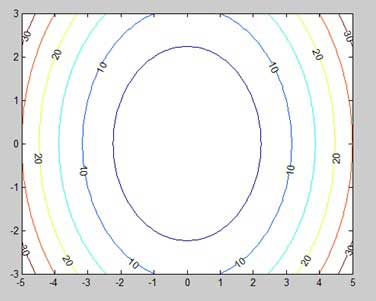
Ba lô chiều

Các đồ thị ba chiều về cơ bản hiển thị một bề mặt được xác định bởi một hàm theo hai biến, g = f (x, y).

Như trước đây, để xác định g, trước tiên chúng ta tạo một tập hợp (x, y) điểm trên miền của hàm bằng cách sử dụng meshgridchỉ huy. Tiếp theo, chúng tôi chỉ định chức năng cho chính nó. Cuối cùng, chúng tôi sử dụngsurf lệnh để tạo một biểu đồ bề mặt.

Ví dụ sau thể hiện khái niệm -

Thí dụ

Hãy để chúng tôi tạo một bản đồ bề mặt 3D cho hàm g = xe ^{- (x 2 + y 2 )}

Tạo một tệp kịch bản và nhập mã sau:

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Khi bạn chạy tệp, MATLAB hiển thị bản đồ 3-D sau:

Bạn cũng có thể sử dụng meshlệnh tạo bề mặt ba chiều. Tuy nhiên,surf lệnh hiển thị cả các đường kết nối và các mặt của bề mặt bằng màu sắc, trong khi, mesh lệnh tạo một bề mặt khung dây với các đường màu nối các điểm xác định.

Cho đến nay, chúng ta đã thấy rằng tất cả các ví dụ đều hoạt động trong MATLAB cũng như GNU của nó, còn được gọi là Octave. Nhưng để giải các phương trình đại số cơ bản, cả MATLAB và Octave đều có chút khác biệt, vì vậy chúng tôi sẽ cố gắng trình bày MATLAB và Octave trong các phần riêng biệt.

Chúng ta cũng sẽ thảo luận về việc phân tích nhân tử và đơn giản hóa các biểu thức đại số.

Giải các phương trình đại số cơ bản trong MATLAB

Các solvehàm được sử dụng để giải các phương trình đại số. Ở dạng đơn giản nhất, hàm giải quyết nhận phương trình được đặt trong dấu ngoặc kép làm đối số.

Ví dụ, chúng ta hãy giải cho x trong phương trình x-5 = 0

solve('x-5=0')

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   5

Bạn cũng có thể gọi hàm giải quyết là -

y = solve('x-5 = 0')

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

y =
   5

Bạn thậm chí có thể không bao gồm vế phải của phương trình -

solve('x-5')

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   5

Nếu phương trình bao gồm nhiều ký hiệu, thì MATLAB theo mặc định sẽ giả định rằng bạn đang giải cho x, tuy nhiên, hàm giải có dạng khác:

solve(equation, variable)

ở đâu, bạn cũng có thể đề cập đến biến.

Ví dụ, chúng ta hãy giải phương trình v - u - 3t ² = 0, với v. Trong trường hợp này, chúng ta nên viết:

solve('v-u-3*t^2=0', 'v')

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   3*t^2 + u

Giải các phương trình đại số cơ bản trong quãng tám

Các roots hàm được sử dụng để giải các phương trình đại số trong Octave và bạn có thể viết các ví dụ trên như sau:

Ví dụ, chúng ta hãy giải cho x trong phương trình x-5 = 0

roots([1, -5])

Octave sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans = 5

Bạn cũng có thể gọi hàm giải quyết là -

y = roots([1, -5])

Octave sẽ thực hiện câu lệnh trên và trả về kết quả sau:

y = 5

Giải phương trình bậc hai trong MATLAB

Các solvehàm cũng có thể giải các phương trình bậc cao. Nó thường được sử dụng để giải phương trình bậc hai. Hàm trả về gốc của phương trình trong một mảng.

Ví dụ sau giải phương trình bậc hai x ² -7x +12 = 0. Tạo tệp script và nhập đoạn mã sau:

eq = 'x^2 -7*x + 12 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

The first root is: 
   3
The second root is: 
   4

Giải phương trình bậc hai trong quãng tám

Ví dụ sau đây giải phương trình bậc hai x ² -7x +12 = 0 trong Octave. Tạo một tệp kịch bản và nhập mã sau:

s = roots([1, -7, 12]);

disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

The first root is: 
   4
The second root is: 
   3

Giải các phương trình bậc cao trong MATLAB

Các solvehàm cũng có thể giải các phương trình bậc cao. Ví dụ, chúng ta hãy giải một phương trình bậc ba là (x-3) ² (x-7) = 0

solve('(x-3)^2*(x-7)=0')

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   3
   3
   7

Trong trường hợp phương trình bậc cao, căn dài chứa nhiều số hạng. Bạn có thể lấy giá trị số của các gốc như vậy bằng cách chuyển chúng thành gấp đôi. Ví dụ sau đây giải phương trình bậc ⁴ x ⁴ - 7x ³ + 3x ² - 5x + 9 = 0.

Tạo một tệp kịch bản và nhập mã sau:

eq = 'x^4 - 7*x^3 + 3*x^2 - 5*x + 9 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
disp('The third root is: '), disp(s(3));
disp('The fourth root is: '), disp(s(4));

% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));

Khi bạn chạy tệp, nó trả về kết quả sau:

The first root is: 
6.630396332390718431485053218985
 The second root is: 
1.0597804633025896291682772499885
 The third root is: 
- 0.34508839784665403032666523448675 - 1.0778362954630176596831109269793*i
 The fourth root is: 
- 0.34508839784665403032666523448675 + 1.0778362954630176596831109269793*i
Numeric value of first root
   6.6304
Numeric value of second root
   1.0598
Numeric value of third root
   -0.3451 - 1.0778i
Numeric value of fourth root
   -0.3451 + 1.0778i

Xin lưu ý rằng hai căn cuối cùng là số phức.

Giải các phương trình bậc cao hơn trong quãng tám

Ví dụ sau đây giải phương trình bậc ⁴ x ⁴ - 7x ³ + 3x ² - 5x + 9 = 0.

Tạo một tệp kịch bản và nhập mã sau:

v = [1, -7,  3, -5, 9];
s = roots(v);

% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));

Khi bạn chạy tệp, nó trả về kết quả sau:

Numeric value of first root
 6.6304
Numeric value of second root
-0.34509 + 1.07784i
Numeric value of third root
-0.34509 - 1.07784i
Numeric value of fourth root
 1.0598

Giải hệ phương trình trong MATLAB

Các solvehàm cũng có thể được sử dụng để tạo ra các nghiệm của hệ phương trình có nhiều hơn một biến. Hãy để chúng tôi lấy một ví dụ đơn giản để chứng minh công dụng này.

Hãy để chúng tôi giải các phương trình -

5x + 9y = 5

3x - 6y = 4

Tạo một tệp kịch bản và nhập mã sau:

s = solve('5*x + 9*y = 5','3*x - 6*y = 4');
s.x
s.y

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans =
   22/19
ans =
   -5/57

Theo cách tương tự, bạn có thể giải các hệ thống tuyến tính lớn hơn. Xét tập phương trình sau:

x + 3y -2z = 5

3x + 5y + 6z = 7

2x + 4y + 3z = 8

Giải hệ phương trình trong quãng tám

Chúng ta có một cách tiếp cận hơi khác để giải hệ phương trình tuyến tính 'n' với ẩn số 'n'. Hãy để chúng tôi lấy một ví dụ đơn giản để chứng minh công dụng này.

Hãy để chúng tôi giải các phương trình -

5x + 9y = 5

3x - 6y = 4

Hệ phương trình tuyến tính như vậy có thể được viết dưới dạng phương trình ma trận đơn Ax = b, trong đó A là ma trận hệ số, b là vectơ cột chứa vế phải của phương trình tuyến tính và x là vectơ cột biểu diễn nghiệm như được hiển thị trong chương trình dưới đây -

Tạo một tệp kịch bản và nhập mã sau:

A = [5, 9; 3, -6];
b = [5;4];
A \ b

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans =

   1.157895
  -0.087719

Theo cách tương tự, bạn có thể giải các hệ thống tuyến tính lớn hơn như được đưa ra bên dưới:

x + 3y -2z = 5

3x + 5y + 6z = 7

2x + 4y + 3z = 8

Mở rộng và Thu thập các phương trình trong MATLAB

Các expand và collecthàm mở rộng và thu thập một phương trình tương ứng. Ví dụ sau minh họa các khái niệm -

Khi bạn làm việc với nhiều hàm tượng trưng, ​​bạn nên khai báo rằng các biến của bạn là biểu tượng.

Tạo một tệp kịch bản và nhập mã sau:

syms x   %symbolic variable x
syms y   %symbolic variable x
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(sin(2*x))
expand(cos(x+y))
 
% collecting equations
collect(x^3 *(x-7))
collect(x^4*(x-3)*(x-5))

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans =
   x^2 + 4*x - 45
ans =
   x^4 + x^3 - 43*x^2 + 23*x + 210
ans =
   2*cos(x)*sin(x)
ans =
   cos(x)*cos(y) - sin(x)*sin(y)
ans =
   x^4 - 7*x^3
ans =
   x^6 - 8*x^5 + 15*x^4

Mở rộng và thu thập phương trình trong quãng tám

Bạn cần phải có symbolic gói, cung cấp expand và collecthàm để mở rộng và thu thập một phương trình, tương ứng. Ví dụ sau minh họa các khái niệm -

Khi bạn làm việc với nhiều hàm tượng trưng, ​​bạn nên khai báo rằng các biến của bạn là biểu tượng nhưng Octave có cách tiếp cận khác để xác định các biến biểu tượng. Lưu ý việc sử dụngSin và Cos, cũng được định nghĩa trong gói biểu tượng.

Tạo một tệp kịch bản và nhập mã sau:

% first of all load the package, make sure its installed.
pkg load symbolic

% make symbols module available
symbols

% define symbolic variables
x = sym ('x');
y = sym ('y');
z = sym ('z');

% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(Sin(2*x))
expand(Cos(x+y))
 
% collecting equations
collect(x^3 *(x-7), z)
collect(x^4*(x-3)*(x-5), z)

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans =

-45.0+x^2+(4.0)*x
ans =

210.0+x^4-(43.0)*x^2+x^3+(23.0)*x
ans =

sin((2.0)*x)
ans =

cos(y+x)
ans =

x^(3.0)*(-7.0+x)
ans =

(-3.0+x)*x^(4.0)*(-5.0+x)

Thừa số hóa và đơn giản hóa biểu thức đại số

Các factor hàm thừa số hóa một biểu thức và simplifyhàm đơn giản hóa một biểu thức. Ví dụ sau thể hiện khái niệm -

Thí dụ

Tạo một tệp kịch bản và nhập mã sau:

syms x
syms y
factor(x^3 - y^3)
factor([x^2-y^2,x^3+y^3])
simplify((x^4-16)/(x^2-4))

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans =
   (x - y)*(x^2 + x*y + y^2)
ans =
   [ (x - y)*(x + y), (x + y)*(x^2 - x*y + y^2)]
ans =
   x^2 + 4

MATLAB cung cấp nhiều cách khác nhau để giải các bài toán về phép tính vi phân và tích phân, giải phương trình vi phân bất kỳ bậc nào và tính các giới hạn. Hơn hết, bạn có thể dễ dàng vẽ đồ thị của các hàm phức tạp và kiểm tra cực đại, cực tiểu và các điểm văn phòng phẩm khác trên đồ thị bằng cách giải hàm gốc, cũng như đạo hàm của nó.

Chương này sẽ giải quyết các vấn đề về giải tích. Trong chương này, chúng ta sẽ thảo luận về các khái niệm tiền giải tích, tức là tính toán giới hạn của hàm số và xác minh các tính chất của giới hạn.

Trong chương tiếp theo Vi phân , chúng ta sẽ tính đạo hàm của một biểu thức và tìm cực đại và cực tiểu cục bộ trên đồ thị. Chúng ta cũng sẽ thảo luận về việc giải các phương trình vi phân.

Cuối cùng, trong chương Tích phân , chúng ta sẽ thảo luận về phép tính tích phân.

Tính toán giới hạn

MATLAB cung cấp limithàm tính toán giới hạn. Ở dạng cơ bản nhất,limit hàm nhận biểu thức làm đối số và tìm giới hạn của biểu thức khi biến độc lập bằng không.

Ví dụ, chúng ta hãy tính giới hạn của một hàm f (x) = (x ³ + 5) / (x ⁴ + 7), vì x có xu hướng bằng không.

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   5/7

Hàm giới hạn thuộc lĩnh vực tính toán tượng trưng; bạn cần sử dụngsymshàm để cho MATLAB biết bạn đang sử dụng biến tượng trưng nào. Bạn cũng có thể tính toán giới hạn của một hàm, vì biến có xu hướng là một số nào đó khác 0. Để tính lim _{x-> a} (f (x)), ta sử dụng lệnh giới hạn với các đối số. Đầu tiên là biểu thức và thứ hai là số, mà x tiếp cận, đây là a .

Ví dụ, chúng ta hãy tính giới hạn của một hàm f (x) = (x-3) / (x-1), vì x có xu hướng là 1.

limit((x - 3)/(x-1),1)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   NaN

Hãy lấy một ví dụ khác,

limit(x^2 + 5, 3)

MATLAB sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   14

Tính toán giới hạn bằng Octave

Sau đây là phiên bản Octave của ví dụ trên bằng cách sử dụng symbolic gói, cố gắng thực thi và so sánh kết quả -

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave sẽ thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   0.7142857142857142857

Xác minh các thuộc tính cơ bản của giới hạn

Định lý giới hạn đại số cung cấp một số tính chất cơ bản của giới hạn. Chúng như sau:

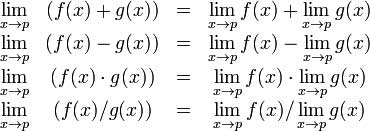
Chúng ta hãy xem xét hai chức năng -

• f (x) = (3x + 5) / (x - 3)
• g (x) = x ² + 1.

Chúng ta hãy tính giới hạn của các hàm khi x có xu hướng bằng 5, của cả hai hàm và xác minh các tính chất cơ bản của giới hạn bằng cách sử dụng hai hàm này và MATLAB.

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

Khi bạn chạy tệp, nó sẽ hiển thị -

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

Xác minh các thuộc tính cơ bản của giới hạn bằng Octave

Sau đây là phiên bản Octave của ví dụ trên bằng cách sử dụng symbolic gói, cố gắng thực thi và so sánh kết quả -

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave sẽ thực hiện câu lệnh trên và trả về kết quả sau:

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

Giới hạn bên trái và bên phải

Khi một hàm có sự gián đoạn đối với một giá trị cụ thể nào đó của biến, giới hạn không tồn tại tại điểm đó. Nói cách khác, giới hạn của hàm f (x) không liên tục tại x = a, khi giá trị của giới hạn, khi x tiếp cận x từ phía bên trái, không bằng giá trị của giới hạn khi x tiếp cận từ phía bên phải.

Điều này dẫn đến khái niệm về giới hạn thuận tay trái và tay phải. Giới hạn thuận tay trái được định nghĩa là giới hạn khi x -> a, từ bên trái, tức là x tiếp cận a, với các giá trị của x <a. Giới hạn thuận tay phải được định nghĩa là giới hạn khi x -> a, từ bên phải, tức là x tiến tới a, với các giá trị của x> a. Khi giới hạn thuận tay trái và giới hạn tay phải không bằng nhau, giới hạn đó không tồn tại.

Chúng ta hãy xem xét một chức năng -

f(x) = (x - 3)/|x - 3|

Ta sẽ chứng tỏ rằng lim _{x-> 3} f (x) không tồn tại. MATLAB giúp chúng tôi xác định thực tế này theo hai cách -

• Bằng cách vẽ đồ thị của hàm số và thể hiện tính gián đoạn.
• Bằng cách tính toán các giới hạn và cho thấy rằng cả hai đều khác nhau.

Giới hạn thuận tay trái và tay phải được tính bằng cách chuyển các chuỗi ký tự 'left' và 'right' cho lệnh giới hạn làm đối số cuối cùng.

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

Khi bạn chạy tệp, MATLAB vẽ sơ đồ sau

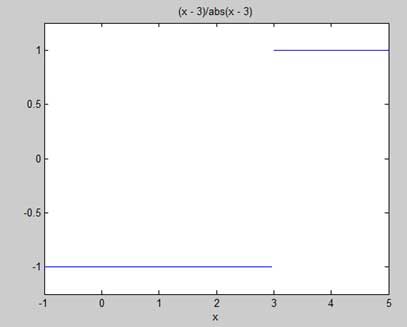
Sau khi đầu ra sau đây được hiển thị -

l =
   -1
  
r =
   1

MATLAB cung cấp difflệnh để tính toán các dẫn xuất biểu tượng. Ở dạng đơn giản nhất, bạn chuyển hàm bạn muốn phân biệt thành lệnh diff làm đối số.

Ví dụ, chúng ta hãy tính đạo hàm của hàm f (t) = 3t ² + 2t ^-2

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

Khi đoạn mã trên được biên dịch và thực thi, nó tạo ra kết quả sau:

ans =
6*t - 4/t^3

Sau đây là tương đương Octave của phép tính trên:

pkg load symbolic
symbols

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

Octave thực thi mã và trả về kết quả sau:

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

Xác minh các Quy tắc Cơ bản về Phân biệt

Hãy để chúng tôi trình bày ngắn gọn các phương trình hoặc quy tắc khác nhau để phân biệt các hàm và xác minh các quy tắc này. Với mục đích này, chúng ta sẽ viết f '(x) cho đạo hàm cấp một và f "(x) cho đạo hàm cấp hai.

Sau đây là các quy tắc để phân biệt -

Quy tắc 1

Với mọi hàm f và g và mọi số thực a và b là đạo hàm của hàm -

h(x) = af(x) + bg(x) đối với x được cho bởi -

h'(x) = af'(x) + bg'(x)

Quy tắc 2

Các sum và subtraction quy tắc phát biểu rằng nếu f và g là hai hàm thì f 'và g' lần lượt là các đạo hàm của chúng, khi đó,

(f + g)' = f' + g'

(f - g)' = f' - g'

Quy tắc 3

Các product quy tắc phát biểu rằng nếu f và g là hai hàm thì f 'và g' lần lượt là đạo hàm của chúng, khi đó,

(f.g)' = f'.g + g'.f

Quy tắc 4

Các quotient quy tắc phát biểu rằng nếu f và g là hai hàm thì f 'và g' lần lượt là đạo hàm của chúng, khi đó,

(f/g)' = (f'.g - g'.f)/g²

Quy tắc 5

Các polynomial hoặc quy tắc quyền lực cơ bản tuyên bố rằng, nếu y = f(x) = xⁿ, sau đó f' = n. x^(n-1)

Kết quả trực tiếp của quy tắc này là đạo hàm của bất kỳ hằng số nào đều bằng 0, tức là nếu y = k, bất kỳ hằng số nào, sau đó

f' = 0

Quy tắc 6

Các chain quy tắc phát biểu rằng, đạo hàm của hàm của một hàm h(x) = f(g(x)) đối với x là,

h'(x)= f'(g(x)).g'(x)

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)
f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)
f = (x^2 + 1)^17
der5 = diff(f)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

Khi bạn chạy tệp, MATLAB hiển thị kết quả sau:

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

Sau đây là tương đương Octave của phép tính trên:

pkg load symbolic
symbols

x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 
f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 
f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 
f = (x^2 + 1)^17 
der5 = differentiate(f,x) 
f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

Octave thực thi mã và trả về kết quả sau:

f =

(2.0+x)*(3.0+x^(2.0))
der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =

(1.0+x^(2.0))^(17.0)
der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x
f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

Đạo hàm của các hàm số mũ, lôgarit và lượng giác

Bảng sau đây cung cấp các đạo hàm của các hàm số mũ, lôgarit và lượng giác thường được sử dụng:

Chức năng	Phát sinh
ca.x	c a.x .ln ca (ln là logarit tự nhiên)
ex	e x
ln x	1 / x
lncx	1 / x.ln c
xx	x x . (1 + ln x)
sin(x)	cos (x)
cos(x)	-sin (x)
tan(x)	giây 2 (x) hoặc 1 / cos 2 (x) hoặc 1 + tan 2 (x)
cot(x)	-csc 2 (x) hoặc -1 / sin 2 (x) hoặc - (1 + cot 2 (x))
sec(x)	giây (x) .tan (x)
csc(x)	-csc (x) .cot (x)

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

syms x
y = exp(x)
diff(y)
y = x^9
diff(y)
y = sin(x)
diff(y)
y = tan(x)
diff(y)
y = cos(x)
diff(y)
y = log(x)
diff(y)
y = log10(x)
diff(y)
y = sin(x)^2
diff(y)
y = cos(3*x^2 + 2*x + 1)
diff(y)
y = exp(x)/sin(x)
diff(y)

Khi bạn chạy tệp, MATLAB hiển thị kết quả sau:

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

Sau đây là tương đương Octave của phép tính trên:

pkg load symbolic
symbols

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

Octave thực thi mã và trả về kết quả sau:

y =

exp(x)
ans =

exp(x)
y =

x^(9.0)
ans =

(9.0)*x^(8.0)
y =

sin(x)
ans =

cos(x)
y =

tan(x)
ans =

1+tan(x)^2
y =

cos(x)
ans =

-sin(x)
y =

log(x)
ans =

x^(-1)
y =

sin(x)^(2.0)
ans =

(2.0)*sin(x)*cos(x)
y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =

sin(x)^(-1)*exp(x)
ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

Tính toán các phái sinh bậc cao hơn

Để tính các đạo hàm cấp cao hơn của hàm f, chúng ta sử dụng cú pháp diff(f,n).

Chúng ta hãy tính đạo hàm cấp hai của hàm số y = f (x) = x .e ^-3x

f = x*exp(-3*x);
diff(f, 2)

MATLAB thực thi mã và trả về kết quả sau:

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

Sau đây là tương đương Octave của phép tính trên:

pkg load symbolic
symbols

x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)

Octave thực thi mã và trả về kết quả sau:

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

Thí dụ

Trong ví dụ này, chúng ta hãy giải quyết một vấn đề. Cho rằng một hàmy = f(x) = 3 sin(x) + 7 cos(5x). Chúng ta sẽ phải tìm xem phương trìnhf" + f = -5cos(2x) đúng.

Tạo một tệp script và nhập mã sau vào đó:

syms x
y = 3*sin(x)+7*cos(5*x);  % defining the function
lhs = diff(y,2)+y;        %evaluting the lhs of the equation
rhs = -5*cos(2*x);        %rhs of the equation
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

Sau đây là tương đương Octave của phép tính trên:

pkg load symbolic
symbols

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);           % defining the function
lhs = differentiate(y, x, 2) + y;  %evaluting the lhs of the equation
rhs = -5*Cos(2*x);                 %rhs of the equation

if(lhs == rhs)
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Octave thực thi mã và trả về kết quả sau:

No, the equation does not hold true
Value of LHS is: 
-(168.0)*cos((5.0)*x)

Tìm cực đại và cực tiểu của đường cong

Nếu chúng ta đang tìm kiếm cực đại và cực tiểu cục bộ cho một đồ thị, về cơ bản chúng ta đang tìm kiếm các điểm cao nhất hoặc thấp nhất trên đồ thị của hàm tại một địa phương cụ thể hoặc cho một phạm vi giá trị cụ thể của biến tượng trưng.

Đối với một hàm số y = f (x), các điểm trên đồ thị mà đồ thị có hệ số góc bằng không được gọi là stationary points. Nói cách khác, điểm đứng yên tại đó f '(x) = 0.

Để tìm điểm đứng yên của một hàm số mà chúng ta phân biệt, chúng ta cần đặt đạo hàm bằng 0 và giải phương trình.

Thí dụ

Ta tìm các điểm đứng yên của hàm số f (x) = 2x ³ + 3x ² - 12x + 17

Thực hiện các bước sau:

First let us enter the function and plot its graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y)

MATLAB thực thi mã và trả về âm mưu sau:

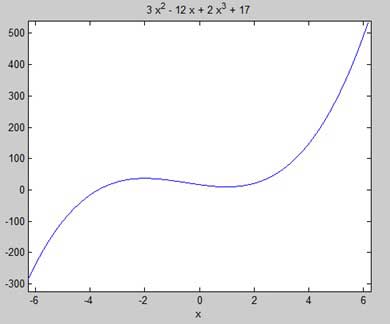
Đây là mã tương đương Octave cho ví dụ trên -

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
print -deps graph.eps

Our aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y, [-2, 2])

MATLAB thực thi mã và trả về âm mưu sau:

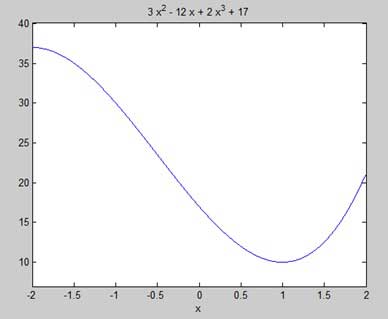
Đây là mã tương đương Octave cho ví dụ trên -

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

Next, let us compute the derivative.

g = diff(y)

MATLAB thực thi mã và trả về kết quả sau:

g =
   6*x^2 + 6*x - 12

Đây là Octave tương đương với phép tính ở trên -

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

Octave thực thi mã và trả về kết quả sau:

g =
   -12.0+(6.0)*x+(6.0)*x^(2.0)

Let us solve the derivative function, g, to get the values where it becomes zero.

s = solve(g)

MATLAB thực thi mã và trả về kết quả sau:

s =
   1
   -2

Sau đây là tương đương Octave của phép tính trên:

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

Octave thực thi mã và trả về kết quả sau:

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =

  -2
   1

This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. Chúng ta có thể thay thế một giá trị trong một hàm tượng trưng bằng cách sử dụng subs chỉ huy.

subs(y, 1), subs(y, -2)

MATLAB thực thi mã và trả về kết quả sau:

ans =
   10
ans =
   37

Sau đây là tương đương Octave của phép tính trên:

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)

ans =
   10.0
ans =
   37.0-4.6734207789940138748E-18*I

Do đó, giá trị nhỏ nhất và lớn nhất của hàm số f (x) = 2x ³ + 3x ² - 12x + 17 trong khoảng [-2,2] là 10 và 37.

Giải phương trình vi phân

MATLAB cung cấp dsolve lệnh để giải phương trình vi phân một cách ký hiệu.

Dạng cơ bản nhất của dsolve lệnh để tìm lời giải cho một phương trình là

dsolve('eqn')

trong đó eqn là một chuỗi văn bản được sử dụng để nhập phương trình.

Nó trả về một giải pháp tượng trưng với một tập hợp các hằng số tùy ý mà MATLAB dán nhãn C1, C2, v.v.

Bạn cũng có thể chỉ định điều kiện ban đầu và điều kiện biên cho vấn đề, dưới dạng danh sách được phân tách bằng dấu phẩy theo sau phương trình dưới dạng:

dsolve('eqn','cond1', 'cond2',…)

Với mục đích sử dụng lệnh dsolve, derivatives are indicated with a D. Ví dụ, một phương trình như f '(t) = -2 * f + cost (t) được nhập dưới dạng:

'Df = -2*f + cos(t)'

Các đạo hàm cấp cao hơn được chỉ ra bằng cách theo sau D theo bậc của đạo hàm.

Ví dụ, phương trình f "(x) + 2f '(x) = 5sin3x sẽ được nhập dưới dạng:

'D2y + 2Dy = 5*sin(3*x)'

Chúng ta hãy lấy một ví dụ đơn giản về phương trình vi phân bậc nhất: y '= 5y.

s = dsolve('Dy = 5*y')

MATLAB thực thi mã và trả về kết quả sau:

s =
   C2*exp(5*t)

Chúng ta hãy lấy một ví dụ khác về phương trình vi phân bậc hai như: y "- y = 0, y (0) = -1, y '(0) = 2.

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

MATLAB thực thi mã và trả về kết quả sau:

ans =
   exp(t)/2 - (3*exp(-t))/2

Tích hợp giải quyết hai loại vấn đề cơ bản khác nhau.

• Trong loại đầu tiên, đạo hàm của một hàm được đưa ra và chúng ta muốn tìm hàm. Do đó, về cơ bản chúng ta đảo ngược quá trình phân hóa. Quá trình ngược lại này được gọi là chống phân biệt, hoặc tìm ra hàm nguyên thủy, hoặc tìm mộtindefinite integral.

• Loại bài toán thứ hai liên quan đến việc cộng một số lượng rất lớn các đại lượng rất nhỏ và sau đó lấy một giới hạn khi kích thước của các đại lượng này tiến dần đến 0, trong khi số lượng số hạng có xu hướng vô cùng. Quá trình này dẫn đến định nghĩa củadefinite integral.

Tích phân xác định được sử dụng để tìm diện tích, thể tích, trọng tâm, mômen quán tính, công được thực hiện bởi một lực và trong nhiều ứng dụng khác.

Tìm tích phân không xác định bằng MATLAB

Theo định nghĩa, nếu đạo hàm của hàm f (x) là f '(x), thì ta nói rằng tích phân bất định của f' (x) đối với x là f (x). Ví dụ, vì đạo hàm (đối với x) của x ² là 2x, chúng ta có thể nói rằng một tích phân không xác định của 2x là x ² .

Trong các ký hiệu -

f'(x²) = 2x, vì thế,

∫ 2xdx = x².

Tích phân không xác định không phải là duy nhất, bởi vì đạo hàm của x ² + c, với bất kỳ giá trị nào của một hằng số c, cũng sẽ là 2x.

Điều này được thể hiện bằng các ký hiệu như -

∫ 2xdx = x² + c.

Trong đó, c được gọi là 'hằng số tùy ý'.

MATLAB cung cấp một intlệnh tính tích phân của một biểu thức. Để suy ra một biểu thức cho tích phân không xác định của một hàm, chúng ta viết:

int(f);

Ví dụ, từ ví dụ trước của chúng tôi -

syms x 
int(2*x)

MATLAB thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   x^2

ví dụ 1

Trong ví dụ này, chúng ta hãy tìm tích phân của một số biểu thức thường dùng. Tạo một tệp script và nhập mã sau vào đó:

syms x n

int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans =
   piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
   -cos(n*t)/n
   ans =
   (a*sin(pi*t))/pi
   ans =
   a^x/log(a)

Ví dụ 2

Tạo một tệp script và nhập mã sau vào đó:

syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))

Lưu ý rằng pretty hàm trả về một biểu thức ở định dạng dễ đọc hơn.

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans =
   sin(x)
 
ans =
   exp(x)
 
ans =
   x*(log(x) - 1)
 
ans =
   log(x)
 
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
                                    2             4 
   24 cos(5 x)   24 x sin(5 x)   12 x  cos(5 x)   x  cos(5 x) 
   ----------- + ------------- - -------------- + ------------ 
      3125            625             125              5 
   
        3             5 
 
   4 x  sin(5 x)   x  sin(5 x) 
   ------------- + ----------- 
         25              5
 
ans =
-1/(4*x^4)
 
ans =
tan(x)
        2 
  x (3 x  - 5 x + 1)
 
ans = 
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
 
      6      5      4    3 
    7 x    3 x    5 x    x 
  - ---- - ---- + ---- + -- 
     12     5      8     2

Tìm tích phân xác định bằng MATLAB

Theo định nghĩa, tích phân xác định về cơ bản là giới hạn của một tổng. Chúng tôi sử dụng các tích phân xác định để tìm các khu vực như diện tích giữa một đường cong và trục x và diện tích giữa hai đường cong. Tích phân xác định cũng có thể được sử dụng trong các trường hợp khác, trong đó đại lượng yêu cầu có thể được biểu thị dưới dạng giới hạn của một tổng.

Các int hàm có thể được sử dụng để tích phân xác định bằng cách vượt qua các giới hạn mà bạn muốn tính tích phân.

Tính toán

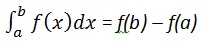
chúng tôi viết,

int(x, a, b)

Ví dụ, để tính toán giá trị của

chúng tôi viết:

int(x, 4, 9)

MATLAB thực hiện câu lệnh trên và trả về kết quả sau:

ans =
   65/2

Sau đây là tương đương Octave của phép tính trên:

pkg load symbolic
symbols

x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);

a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));

Octave thực thi mã và trả về kết quả sau:

Area: 

   32.500

Một giải pháp thay thế có thể được đưa ra bằng cách sử dụng hàm quad () do Octave cung cấp như sau:

pkg load symbolic
symbols

f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);

display('Area: '), disp(double(a));

Octave thực thi mã và trả về kết quả sau:

Area: 
   32.500

ví dụ 1

Chúng ta hãy tính diện tích nằm giữa trục x và đường cong y = x ³ −2x + 5 và các hoành độ x = 1 và x = 2.

Diện tích bắt buộc được đưa ra bởi -

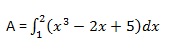
Tạo một tệp kịch bản và nhập mã sau:

f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

a =
23/4
Area: 
   5.7500

Sau đây là tương đương Octave của phép tính trên:

pkg load symbolic
symbols

x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);

a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));

Octave thực thi mã và trả về kết quả sau:

Area: 

   5.7500

Một giải pháp thay thế có thể được đưa ra bằng cách sử dụng hàm quad () do Octave cung cấp như sau:

pkg load symbolic
symbols

x = sym("x");
f = inline("x^3 - 2*x +5");

[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));

Octave thực thi mã và trả về kết quả sau:

Area: 
   5.7500

Ví dụ 2

Tìm diện tích dưới đường cong: f (x) = x ² cos (x) với −4 ≤ x ≤ 9.

Tạo tệp kịch bản và viết mã sau:

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

Khi bạn chạy tệp, MATLAB vẽ biểu đồ -

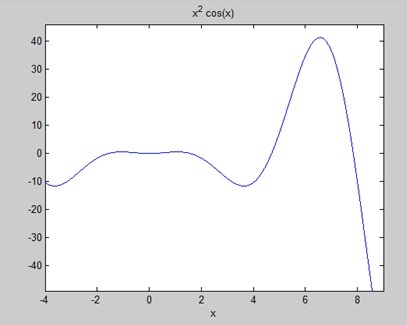
Đầu ra được đưa ra dưới đây -

a = 
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

Sau đây là tương đương Octave của phép tính trên:

pkg load symbolic
symbols

x = sym("x");
f = inline("x^2*cos(x)");

ezplot(f, [-4,9])
print -deps graph.eps

[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));

MATLAB biểu diễn đa thức dưới dạng vectơ hàng chứa các hệ số được sắp xếp theo lũy thừa giảm dần. Ví dụ, phương trình P (x) = x ⁴ + 7x ³ - 5x + 9 có thể được biểu diễn dưới dạng:

p = [1 7 0 -5 9];

Đánh giá đa thức

Các polyvalhàm được sử dụng để đánh giá một đa thức tại một giá trị xác định. Ví dụ: để đánh giá đa thức trước của chúng tap, tại x = 4, nhập -

p = [1 7 0  -5 9];
polyval(p,4)

MATLAB thực hiện các câu lệnh trên và trả về kết quả sau:

ans = 693

MATLAB cũng cung cấp polyvalmhàm đánh giá đa thức ma trận. Đa thức ma trận là mộtpolynomial với ma trận là biến.

Ví dụ, chúng ta hãy tạo một ma trận vuông X và đánh giá đa thức p, tại X -

p = [1 7 0  -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)

MATLAB thực hiện các câu lệnh trên và trả về kết quả sau:

ans =
      2307       -1769        -939        4499
      2314       -2376        -249        4695
      2256       -1892        -549        4310
      4570       -4532       -1062        9269

Tìm gốc rễ của đa thức

Các rootshàm tính toán các căn của một đa thức. Ví dụ, để tính số gốc của đa thức p, hãy nhập -

p = [1 7 0  -5 9];
r = roots(p)

MATLAB thực hiện các câu lệnh trên và trả về kết quả sau:

r =
   -6.8661 + 0.0000i
   -1.4247 + 0.0000i
   0.6454 + 0.7095i
   0.6454 - 0.7095i

Chức năng polylà một nghịch đảo của hàm gốc và trả về các hệ số đa thức. Ví dụ -

p2 = poly(r)

MATLAB thực hiện các câu lệnh trên và trả về kết quả sau:

p2 =

   Columns 1 through 3:

      1.00000 + 0.00000i   7.00000 + 0.00000i   0.00000 + 0.00000i

   Columns 4 and 5:

      -5.00000 - 0.00000i   9.00000 + 0.00000i

Phù hợp đường cong đa thức

Các polyfithàm tìm các hệ số của đa thức phù hợp với tập dữ liệu theo nghĩa bình phương nhỏ nhất. Nếu x và y là hai vectơ chứa dữ liệu x và y được lắp vào một đa thức bậc n, thì chúng ta nhận được đa thức vừa với dữ liệu bằng cách viết:

p = polyfit(x,y,n)

Thí dụ

Tạo một tệp kịch bản và nhập mã sau:

x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67];   %data
p = polyfit(x,y,4)   %get the polynomial

% Compute the values of the polyfit estimate over a finer range, 
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;          
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on

Khi bạn chạy tệp, MATLAB hiển thị kết quả sau:

p =
   4.1056  -47.9607  222.2598 -362.7453  191.1250

Và vẽ biểu đồ sau:

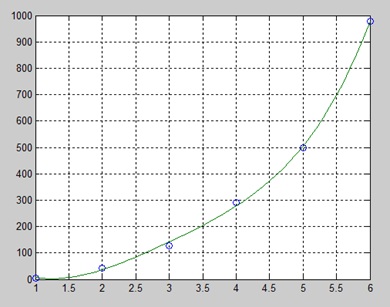
MATLAB cung cấp lệnh để làm việc với các phép biến đổi, chẳng hạn như các phép biến đổi Laplace và Fourier. Biến đổi được sử dụng trong khoa học và kỹ thuật như một công cụ để đơn giản hóa việc phân tích và xem xét dữ liệu từ một góc độ khác.

Ví dụ, phép biến đổi Fourier cho phép chúng ta chuyển đổi một tín hiệu được biểu diễn dưới dạng hàm của thời gian thành hàm của tần số. Phép biến đổi Laplace cho phép chúng ta chuyển một phương trình vi phân thành một phương trình đại số.

MATLAB cung cấp laplace, fourier và fft lệnh để làm việc với các phép biến đổi Laplace, Fourier và Fast Fourier.

Biến đổi Laplace

Biến đổi Laplace của một hàm theo thời gian f (t) được cho bởi tích phân sau:

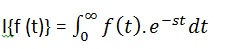
Biến đổi Laplace cũng được ký hiệu là biến đổi f (t) thành F (s). Bạn có thể thấy quá trình biến đổi hoặc tích hợp này chuyển đổi f (t), một hàm của biến biểu tượng t, thành một hàm F (s) khác, với một biến s khác.

Phép biến đổi Laplace biến các phương trình vi phân thành các phương trình đại số. Để tính biến đổi Laplace của hàm f (t), hãy viết:

laplace(f(t))

Thí dụ

Trong ví dụ này, chúng ta sẽ tính toán phép biến đổi Laplace của một số hàm thường được sử dụng.

Tạo một tệp kịch bản và nhập mã sau:

syms s t a b w

laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans =
   1/s^2

ans =
   2/s^3

ans =
   362880/s^10

ans =
   1/(b + s)
  
ans =
   w/(s^2 + w^2)
  
ans =
   s/(s^2 + w^2)

Biến đổi Laplace ngược

MATLAB cho phép chúng tôi tính toán biến đổi Laplace ngược bằng lệnh ilaplace.

Ví dụ,

ilaplace(1/s^3)

MATLAB sẽ thực hiện câu lệnh trên và hiển thị kết quả:

ans =
   t^2/2

Thí dụ

Tạo một tệp kịch bản và nhập mã sau:

syms s t a b w

ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

ans =
   t^6/720

ans =
   2*exp(-t*w)

ans =
   cos(2*t)

ans =
   ilaplace(exp(-b*t), t, x)

ans =
   sin(t*w)

ans =
   cos(t*w)

Biến đổi Fourier

Phép biến đổi Fourier thường biến một hàm toán học của thời gian, f (t), thành một hàm mới, đôi khi được ký hiệu là hoặc F, có đối số là tần số với đơn vị là chu kỳ / s (hertz) hoặc radian trên giây. Khi đó, hàm mới được gọi là phép biến đổi Fourier và / hoặc phổ tần số của hàm f.

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

syms x 
f = exp(-2*x^2);     %our function
ezplot(f,[-2,2])     % plot of our function
FT = fourier(f)      % Fourier transform

Khi bạn chạy tệp, MATLAB vẽ biểu đồ sau:

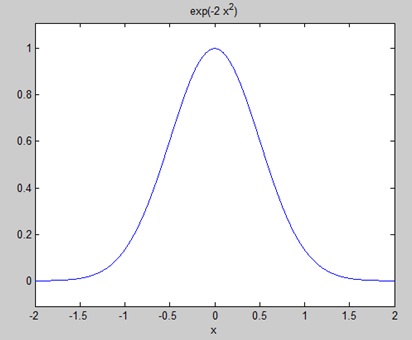
Kết quả sau được hiển thị:

FT =
   (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2

Vẽ biểu đồ biến đổi Fourier dưới dạng:

ezplot(FT)

Đưa ra biểu đồ sau:

Biến đổi Fourier ngược

MATLAB cung cấp ifourierlệnh để tính toán biến đổi Fourier nghịch đảo của một hàm. Ví dụ,

f = ifourier(-2*exp(-abs(w)))

MATLAB sẽ thực hiện câu lệnh trên và hiển thị kết quả:

f =
   -2/(pi*(x^2 + 1))

GNU Octave là một ngôn ngữ lập trình cấp cao giống như MATLAB và nó hầu như tương thích với MATLAB. Nó cũng được sử dụng để tính toán số.

Octave có các tính năng phổ biến sau với MATLAB:

• ma trận là kiểu dữ liệu cơ bản
• nó có hỗ trợ tích hợp cho các số phức
• nó có các hàm và thư viện toán học được tích hợp sẵn
• nó hỗ trợ các chức năng do người dùng xác định

GNU Octave cũng là phần mềm có thể phân phối lại miễn phí. Bạn có thể phân phối lại và / hoặc sửa đổi nó theo các điều khoản của Giấy phép Công cộng GNU (GPL) do Tổ chức Phần mềm Tự do xuất bản.

MATLAB so với Octave

Hầu hết các chương trình MATLAB chạy trong Octave, nhưng một số chương trình Octave có thể không chạy trong MATLAB vì Octave cho phép một số cú pháp mà MATLAB thì không.

Ví dụ: MATLAB chỉ hỗ trợ dấu nháy đơn, nhưng Octave hỗ trợ cả dấu nháy đơn và dấu nháy kép để xác định chuỗi. Nếu bạn đang tìm kiếm một hướng dẫn về Octave, vui lòng xem qua hướng dẫn này từ đầu, bao gồm cả MATLAB cũng như Octave.

Các ví dụ tương thích

Hầu hết tất cả các ví dụ được đề cập trong hướng dẫn này đều tương thích với MATLAB cũng như Octave. Hãy thử ví dụ sau trong MATLAB và Octave tạo ra cùng một kết quả mà không có bất kỳ thay đổi cú pháp nào -

Ví dụ này tạo một bản đồ bề mặt 3D cho hàm g = xe ^{- (x 2 + y 2 )} . Tạo một tệp kịch bản và nhập mã sau:

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Khi bạn chạy tệp, MATLAB hiển thị bản đồ 3-D sau:

Ví dụ không tương thích

Mặc dù tất cả các chức năng cốt lõi của MATLAB đều có sẵn trong Octave, nhưng có một số chức năng, chẳng hạn như Phép tính Tích phân & Tích hợp, không khớp chính xác trong cả hai ngôn ngữ. Hướng dẫn này đã cố gắng đưa ra cả hai loại ví dụ mà chúng khác nhau về cú pháp của chúng.

Hãy xem xét ví dụ sau trong đó MATLAB và Octave sử dụng các hàm khác nhau để lấy diện tích của một đường cong: f (x) = x ² cos (x) cho −4 ≤ x ≤ 9. Sau đây là phiên bản MATLAB của mã:

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

Khi bạn chạy tệp, MATLAB vẽ biểu đồ -

Kết quả sau được hiển thị

a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

Nhưng để cung cấp diện tích của cùng một đường cong trong Octave, bạn sẽ phải sử dụng symbolic gói như sau -

pkg load symbolic
symbols

x = sym("x");
f = inline("x^2*cos(x)");

ezplot(f, [-4,9])
print -deps graph.eps

[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));

Simulink là một môi trường thiết kế mô phỏng và dựa trên mô hình cho các hệ thống động và nhúng, được tích hợp với MATLAB. Simulink, cũng được phát triển bởi MathWorks, là một công cụ ngôn ngữ lập trình đồ họa luồng dữ liệu để mô hình hóa, mô phỏng và phân tích các hệ thống động đa miền. Về cơ bản, nó là một công cụ sơ đồ khối đồ họa với bộ thư viện khối có thể tùy chỉnh.

Nó cho phép bạn kết hợp các thuật toán MATLAB vào các mô hình cũng như xuất kết quả mô phỏng sang MATLAB để phân tích thêm.

Simulink hỗ trợ -

• thiết kế cấp hệ thống
• simulation
• tạo mã tự động
• kiểm tra và xác minh các hệ thống nhúng

Có một số sản phẩm bổ trợ khác do MathWorks cung cấp và các sản phẩm phần cứng và phần mềm của bên thứ ba có sẵn để sử dụng với Simulink.

Danh sách sau đây mô tả ngắn gọn về một số trong số chúng -

• Stateflow cho phép phát triển các máy trạng thái và lưu đồ.

• Simulink Coder cho phép tạo mã nguồn C để thực hiện các hệ thống theo thời gian thực một cách tự động.

• xPC Target cùng với x86-based real-time systems cung cấp môi trường để mô phỏng và kiểm tra các mô hình Simulink và Stateflow trong thời gian thực trên hệ thống vật lý.

• Embedded Coder hỗ trợ các mục tiêu nhúng cụ thể.

• HDL Coder cho phép tự động tạo VHDL tổng hợp và Verilog.

• SimEvents cung cấp một thư viện các khối xây dựng đồ họa để mô hình hóa hệ thống xếp hàng.

Simulink có khả năng xác minh và xác nhận có hệ thống các mô hình thông qua việc kiểm tra kiểu mô hình, truy xuất nguồn gốc các yêu cầu và phân tích vùng phủ của mô hình.

Simulink Design Verifier cho phép bạn xác định các lỗi thiết kế và tạo các tình huống test case để kiểm tra mô hình.

Sử dụng Simulink

Để mở Simulink, hãy nhập vùng làm việc MATLAB -

simulink

Simulink mở ra với Library Browser. Trình duyệt Thư viện được sử dụng để xây dựng các mô hình mô phỏng.

Ở khung cửa sổ bên trái, bạn sẽ tìm thấy một số thư viện được phân loại dựa trên các hệ thống khác nhau, nhấp vào từng thư viện sẽ hiển thị các khối thiết kế trên khung cửa sổ bên phải.

Xây dựng mô hình

Để tạo một mô hình mới, hãy nhấp vào Newtrên thanh công cụ của Trình duyệt Thư viện. Thao tác này sẽ mở ra một cửa sổ mô hình mới không có tiêu đề.

Mô hình Simulink là một sơ đồ khối.

Các phần tử mô hình được thêm vào bằng cách chọn các phần tử thích hợp từ Trình duyệt Thư viện và kéo chúng vào cửa sổ Mô hình.

Ngoài ra, bạn có thể sao chép các phần tử mô hình và dán chúng vào cửa sổ mô hình.

Ví dụ

Kéo và thả các mục từ thư viện Simulink để tạo dự án của bạn.

Đối với mục đích của ví dụ này, hai khối sẽ được sử dụng cho mô phỏng - A Source (một tín hiệu) và một Sink(phạm vi). Một bộ tạo tín hiệu (nguồn) tạo ra một tín hiệu tương tự, tín hiệu này sau đó sẽ được hiển thị bằng đồ thị bởi phạm vi (phần chìm).

Bắt đầu bằng cách kéo các khối bắt buộc từ thư viện vào cửa sổ dự án. Sau đó, kết nối các khối với nhau có thể được thực hiện bằng cách kéo các trình kết nối từ các điểm kết nối trên khối này sang các điểm kết nối của khối khác.

Hãy để chúng tôi kéo một khối 'Sine Wave' vào mô hình.

Chọn 'Chìm' từ thư viện và kéo khối 'Phạm vi' vào mô hình.

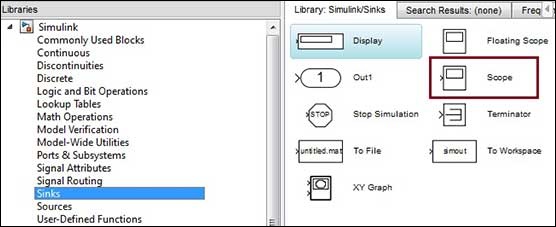
Kéo một đường tín hiệu từ đầu ra của khối Sine Wave đến đầu vào của khối Scope.

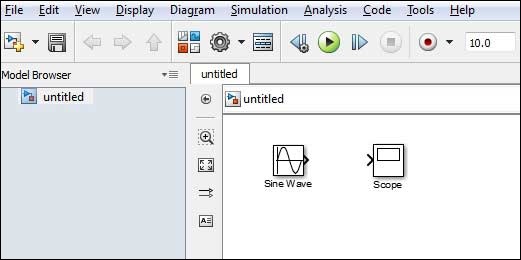
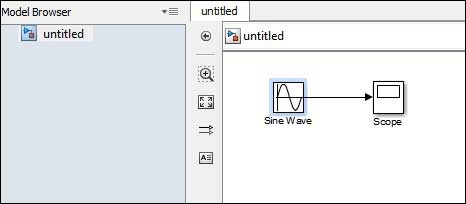
Chạy mô phỏng bằng cách nhấn 'Runnút ', giữ tất cả các tham số mặc định (bạn có thể thay đổi chúng từ menu Mô phỏng)

Bạn sẽ nhận được đồ thị dưới đây từ phạm vi.