MATLAB - Toán tử
Một toán tử là một ký hiệu yêu cầu trình biên dịch thực hiện các thao tác toán học hoặc logic cụ thể. MATLAB được thiết kế để hoạt động chủ yếu trên toàn bộ ma trận và mảng. Do đó, các toán tử trong MATLAB hoạt động trên cả dữ liệu vô hướng và không vô hướng. MATLAB cho phép các loại hoạt động cơ bản sau:
- Toán tử số học
- Toán tử quan hệ
- Toán tử logic
- Hoạt động Bitwise
- Đặt hoạt động
Toán tử số học
MATLAB cho phép hai loại phép toán số học khác nhau -
- Phép toán số học ma trận
- Phép toán số học mảng
Các phép toán số học ma trận giống như được định nghĩa trong đại số tuyến tính. Các phép toán mảng được thực thi từng phần tử, cả trên mảng một chiều và nhiều chiều.
Các toán tử ma trận và toán tử mảng được phân biệt bằng ký hiệu dấu chấm (.). Tuy nhiên, vì phép toán cộng và trừ giống nhau đối với ma trận và mảng, nên toán tử giống nhau cho cả hai trường hợp. Bảng sau đây mô tả ngắn gọn về các toán tử:
Hiển thị các ví dụ
| Sr.No. | Nhà điều hành & Mô tả |
|---|---|
| 1 | + Phép cộng hoặc cộng một bậc. A + B thêm các giá trị được lưu trữ trong các biến A và B. A và B phải có cùng kích thước, trừ khi một là vô hướng. Một đại lượng vô hướng có thể được thêm vào ma trận có kích thước bất kỳ. |
| 2 | - Phép trừ hoặc trừ một bậc. AB trừ giá trị của B cho A. A và B phải có cùng kích thước, trừ khi một là vô hướng. Một đại lượng vô hướng có thể được trừ khỏi một ma trận có kích thước bất kỳ. |
| 3 | * Phép nhân ma trận. C = A * B là tích đại số tuyến tính của ma trận A và B. Chính xác hơn,
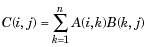
Đối với A và B không vô hướng, số cột của A phải bằng số hàng của B. Một vô hướng có thể nhân một ma trận có kích thước bất kỳ. |
| 4 | .* Phép nhân mảng. A. * B là tích từng phần tử của mảng A và B. A và B phải có cùng kích thước, trừ khi một trong số chúng là vô hướng. |
| 5 | / Gạch chéo hoặc phân chia bên phải ma trận. B / A gần giống với B * inv (A). Chính xác hơn, B / A = (A '\ B') '. |
| 6 | ./ Phép chia phải mảng. A./B là ma trận có các phần tử A (i, j) / B (i, j). A và B phải có cùng kích thước, trừ khi một trong số chúng là vô hướng. |
| 7 | \ Dấu gạch chéo ngược hoặc phép chia trái ma trận. Nếu A là ma trận vuông, A \ B gần giống như inv (A) * B, ngoại trừ nó được tính theo một cách khác. Nếu A là một n-by-n ma trận và B là một vector cột với các thành phần n, hay một ma trận với một số cột như vậy, sau đó X = A \ B là giải pháp cho phương trình AX = B . Một thông báo cảnh báo được hiển thị nếu A có tỷ lệ kém hoặc gần như số ít. |
| số 8 | .\ Mảng chia trái. A. \ B là ma trận có các phần tử B (i, j) / A (i, j). A và B phải có cùng kích thước, trừ khi một trong số chúng là vô hướng. |
| 9 | ^ Quyền lực ma trận. X ^ p là X thành lũy thừa p, nếu p là một vô hướng. Nếu p là số nguyên, lũy thừa được tính bằng bình phương lặp lại. Nếu số nguyên là số âm thì X được đảo ngược trước. Đối với các giá trị khác của p, phép tính liên quan đến giá trị riêng và giá trị riêng, sao cho nếu [V, D] = eig (X), thì X ^ p = V * D. ^ p / V. |
| 10 | .^ Sức mạnh mảng. A. ^ B là ma trận có các phần tử A (i, j) thành lũy thừa B (i, j). A và B phải có cùng kích thước, trừ khi một trong số chúng là vô hướng. |
| 11 | ' Chuyển vị ma trận. A 'là phép chuyển vị đại số tuyến tính của A. Đối với ma trận phức, đây là phép chuyển vị liên hợp phức. |
| 12 | .' Chuyển vị mảng. A. ' là mảng chuyển vị của A. Đối với ma trận phức, điều này không liên quan đến phép cộng hợp. |
Toán tử quan hệ
Toán tử quan hệ cũng có thể hoạt động trên cả dữ liệu vô hướng và không vô hướng. Toán tử quan hệ cho mảng thực hiện so sánh từng phần tử giữa hai mảng và trả về một mảng logic có cùng kích thước, với các phần tử được đặt thành lôgic 1 (true) trong đó quan hệ là đúng và các phần tử được đặt thành lôgic 0 (sai) ở đó không phải.
Bảng sau đây cho thấy các toán tử quan hệ có sẵn trong MATLAB:
Hiển thị các ví dụ
| Sr.No. | Nhà điều hành & Mô tả |
|---|---|
| 1 | < Ít hơn |
| 2 | <= Ít hơn hoặc bằng |
| 3 | > Lớn hơn |
| 4 | >= Lớn hơn hoặc bằng |
| 5 | == Tương đương với |
| 6 | ~= Không bằng |
Toán tử logic
MATLAB cung cấp hai loại toán tử và hàm logic -
Phần tử khôn ngoan - Các toán tử này hoạt động trên các phần tử tương ứng của mảng logic.
Ngắn mạch - Các toán tử này hoạt động trên các biểu thức vô hướng và logic.
Toán tử logic khôn ngoan phần tử hoạt động từng phần tử trên mảng logic. Các ký hiệu &, |, và ~ là các toán tử mảng logic AND, OR và NOT.
Các toán tử logic ngắn mạch cho phép đoản mạch trên các hoạt động logic. Các ký hiệu && và || là các toán tử ngắn mạch logic AND và OR.
Hiển thị các ví dụ
Hoạt động Bitwise
Toán tử bitwise làm việc trên các bit và thực hiện hoạt động từng bit. Bảng sự thật cho &, |, và ^ như sau:
| p | q | p & q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Giả sử nếu A = 60; và B = 13; Bây giờ ở định dạng nhị phân, chúng sẽ như sau:
A = 0011 1100
B = 0000 1101
-----------------
A&B = 0000 1100
A | B = 0011 1101
A ^ B = 0011 0001
~ A = 1100 0011
MATLAB cung cấp các chức năng khác nhau cho các hoạt động theo bit như hoạt động 'bitwise và', 'theo chiều bit hoặc' và 'không theo chiều bit', hoạt động shift, v.v.
Bảng sau đây cho thấy các phép toán bitwise thường được sử dụng:
Hiển thị các ví dụ
| Chức năng | Mục đích |
|---|---|
| bitand (a, b) | Bit-khôn ngoan AND của số nguyên a và b |
| bitcmp (a) | Sự bổ sung khôn ngoan của một |
| bitget (a, pos) | Nhận bit tại vị trí xác định pos , trong mảng số nguyên a |
| bitor (a, b) | OR-khôn ngoan của số nguyên a và b |
| bitet (a, pos) | Set bit tại địa điểm cụ thể pos của một |
| bithift (a, k) | Trả về một chuyển sang trái của k bit, tương đương với nhân với 2 k . Giá trị âm của k tương ứng với các bit dịch sang phải hoặc chia cho 2 | k | và làm tròn đến số nguyên gần nhất theo hướng âm vô hạn. Mọi bit tràn đều bị cắt bớt. |
| bitxor (a, b) | XOR bit khôn ngoan của số nguyên a và b |
| hoán đổi | Trao đổi thứ tự byte |
Đặt hoạt động
MATLAB cung cấp các chức năng khác nhau cho các hoạt động tập hợp, như liên hợp, giao điểm và kiểm tra thành viên tập hợp, v.v.
Bảng sau đây cho thấy một số hoạt động tập hợp thường được sử dụng:
Hiển thị các ví dụ
| Sr.No. | Mô tả chức năng |
|---|---|
| 1 | intersect(A,B) Đặt giao điểm của hai mảng; trả về các giá trị chung cho cả A và B. Các giá trị trả về được sắp xếp theo thứ tự. |
| 2 | intersect(A,B,'rows') Xử lý mỗi hàng A và mỗi hàng B là các thực thể đơn lẻ và trả về các hàng chung cho cả A và B. Các hàng của ma trận trả về được sắp xếp theo thứ tự. |
| 3 | ismember(A,B) Trả về một mảng có cùng kích thước với A, chứa 1 (true) trong đó các phần tử của A được tìm thấy trong B. Ở những nơi khác, nó trả về 0 (false). |
| 4 | ismember(A,B,'rows') Xử lý mỗi hàng A và mỗi hàng B là các thực thể đơn lẻ và trả về một vectơ chứa 1 (đúng) trong đó các hàng của ma trận A cũng là các hàng B. Ở những nơi khác, nó trả về 0 (sai). |
| 5 | issorted(A) Trả về lôgic 1 (đúng) nếu các phần tử của A theo thứ tự được sắp xếp và lôgic 0 (sai) nếu ngược lại. Đầu vào A có thể là một vectơ hoặc một mảng ô N-x 1 hoặc 1 x N gồm các chuỗi.A is considered to be sorted if A và đầu ra của sắp xếp (A) là bằng nhau. |
| 6 | issorted(A, 'rows') Trả về lôgic 1 (đúng) nếu các hàng của ma trận hai chiều A theo thứ tự được sắp xếp và lôgic 0 (sai) nếu ngược lại. Matrix A is considered to be sorted if A và đầu ra của máy sắp xếp (A) bằng nhau. |
| 7 | setdiff(A,B) Đặt hiệu của hai mảng; trả về các giá trị trong A không có trong B. Các giá trị trong mảng được trả về được sắp xếp theo thứ tự. |
| số 8 | setdiff(A,B,'rows') Xử lý mỗi hàng A và mỗi hàng B là các thực thể đơn lẻ và trả về các hàng từ A không có trong B. Các hàng của ma trận trả về được sắp xếp theo thứ tự. Tùy chọn 'hàng' không hỗ trợ mảng ô. |
| 9 | setxor Đặt HOẶC riêng của hai mảng |
| 10 | union Đặt sự kết hợp của hai mảng |
| 11 | unique Giá trị duy nhất trong mảng |