MATLAB - Sự khác biệt

MATLAB cung cấp difflệnh để tính toán các dẫn xuất biểu tượng. Ở dạng đơn giản nhất, bạn chuyển hàm bạn muốn phân biệt sang lệnh diff làm đối số.

Ví dụ, chúng ta hãy tính đạo hàm của hàm f (t) = 3t ² + 2t ^-2

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

Khi đoạn mã trên được biên dịch và thực thi, nó tạo ra kết quả sau:

ans =
6*t - 4/t^3

Sau đây là Octave tương đương với phép tính trên:

pkg load symbolic
symbols

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

Octave thực thi mã và trả về kết quả sau:

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

Xác minh các Quy tắc Cơ bản về Phân biệt

Hãy để chúng tôi nêu ngắn gọn các phương trình hoặc quy tắc khác nhau để phân biệt các hàm và xác minh các quy tắc này. Với mục đích này, chúng ta sẽ viết f '(x) cho đạo hàm cấp một và f "(x) cho đạo hàm cấp hai.

Sau đây là các quy tắc để phân biệt -

Quy tắc 1

Với mọi hàm f và g và mọi số thực a và b là đạo hàm của hàm -

h(x) = af(x) + bg(x) đối với x được cho bởi -

h'(x) = af'(x) + bg'(x)

Quy tắc 2

Các sum và subtraction quy tắc phát biểu rằng nếu f và g là hai hàm thì f 'và g' lần lượt là các đạo hàm của chúng, khi đó,

(f + g)' = f' + g'

(f - g)' = f' - g'

Quy tắc 3

Các product quy tắc phát biểu rằng nếu f và g là hai hàm thì f 'và g' lần lượt là các đạo hàm của chúng, khi đó,

(f.g)' = f'.g + g'.f

Quy tắc 4

Các quotient quy tắc phát biểu rằng nếu f và g là hai hàm thì f 'và g' lần lượt là các đạo hàm của chúng, khi đó,

(f/g)' = (f'.g - g'.f)/g²

Quy tắc 5

Các polynomial hoặc quy tắc quyền lực cơ bản tuyên bố rằng, nếu y = f(x) = xⁿ, sau đó f' = n. x^(n-1)

Kết quả trực tiếp của quy tắc này là đạo hàm của bất kỳ hằng số nào bằng 0, tức là, nếu y = k, bất kỳ hằng số nào, sau đó

f' = 0

Quy tắc 6

Các chain quy tắc phát biểu rằng, đạo hàm của hàm của một hàm h(x) = f(g(x)) đối với x là,

h'(x)= f'(g(x)).g'(x)

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)

f = (x^2 + 1)^17
der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

Khi bạn chạy tệp, MATLAB hiển thị kết quả sau:

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

Sau đây là Octave tương đương với phép tính trên:

pkg load symbolic
symbols

x = sym("x");
t = sym("t");

f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 

f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 

f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 

f = (x^2 + 1)^17 
der5 = differentiate(f,x) 

f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

Octave thực thi mã và trả về kết quả sau:

f =

(2.0+x)*(3.0+x^(2.0))
der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =

(1.0+x^(2.0))^(17.0)
der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x
f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

Đạo hàm của các hàm số mũ, lôgarit và lượng giác

Bảng sau đây cung cấp các đạo hàm của các hàm số mũ, lôgarit và lượng giác thường được sử dụng:

Chức năng	Phát sinh
c^a.x	c ^a.x .ln ca (ln là logarit tự nhiên)
e^x	e ^x
ln x	1 / x
ln_cx	1 / x.ln c
x^x	x ^x . (1 + ln x)
sin(x)	cos (x)
cos(x)	-sin (x)
tan(x)	giây ² (x) hoặc 1 / cos ² (x) hoặc 1 + tan ² (x)
cot(x)	-csc ² (x) hoặc -1 / sin ² (x) hoặc - (1 + cot ² (x))
sec(x)	giây (x) .tan (x)
csc(x)	-csc (x) .cot (x)

Thí dụ

Tạo một tệp script và nhập mã sau vào đó:

syms x
y = exp(x)
diff(y)

y = x^9
diff(y)

y = sin(x)
diff(y)

y = tan(x)
diff(y)

y = cos(x)
diff(y)

y = log(x)
diff(y)

y = log10(x)
diff(y)

y = sin(x)^2
diff(y)

y = cos(3*x^2 + 2*x + 1)
diff(y)

y = exp(x)/sin(x)
diff(y)

Khi bạn chạy tệp, MATLAB hiển thị kết quả sau:

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

Sau đây là Octave tương đương với phép tính trên:

pkg load symbolic
symbols

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

Octave thực thi mã và trả về kết quả sau:

y =

exp(x)
ans =

exp(x)
y =

x^(9.0)
ans =

(9.0)*x^(8.0)
y =

sin(x)
ans =

cos(x)
y =

tan(x)
ans =

1+tan(x)^2
y =

cos(x)
ans =

-sin(x)
y =

log(x)
ans =

x^(-1)
y =

sin(x)^(2.0)
ans =

(2.0)*sin(x)*cos(x)
y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =

sin(x)^(-1)*exp(x)
ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

Tính toán các phái sinh bậc cao hơn

Để tính các đạo hàm cấp cao hơn của hàm f, chúng ta sử dụng cú pháp diff(f,n).

Chúng ta hãy tính đạo hàm cấp hai của hàm số y = f (x) = x .e ^-3x

f = x*exp(-3*x);
diff(f, 2)

MATLAB thực thi mã và trả về kết quả sau:

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

Sau đây là Octave tương đương với phép tính trên:

pkg load symbolic
symbols

x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)

Octave thực thi mã và trả về kết quả sau:

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

Thí dụ

Trong ví dụ này, chúng ta hãy giải quyết một vấn đề. Cho rằng một hàmy = f(x) = 3 sin(x) + 7 cos(5x). Chúng ta sẽ phải tìm xem phương trìnhf" + f = -5cos(2x) đúng.

Tạo một tệp script và nhập mã sau vào đó:

syms x
y = 3*sin(x)+7*cos(5*x);  % defining the function
lhs = diff(y,2)+y;        %evaluting the lhs of the equation
rhs = -5*cos(2*x);        %rhs of the equation
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Khi bạn chạy tệp, nó sẽ hiển thị kết quả sau:

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

Sau đây là Octave tương đương với phép tính trên:

pkg load symbolic
symbols

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);           % defining the function
lhs = differentiate(y, x, 2) + y;  %evaluting the lhs of the equation
rhs = -5*Cos(2*x);                 %rhs of the equation

if(lhs == rhs)
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Octave thực thi mã và trả về kết quả sau:

No, the equation does not hold true
Value of LHS is: 
-(168.0)*cos((5.0)*x)

Tìm cực đại và cực tiểu của đường cong

Nếu chúng ta đang tìm kiếm cực đại và cực tiểu cục bộ cho đồ thị, về cơ bản chúng ta đang tìm điểm cao nhất hoặc thấp nhất trên đồ thị của hàm tại một địa phương cụ thể hoặc cho một phạm vi giá trị cụ thể của biến tượng trưng.

Đối với một hàm số y = f (x), các điểm trên đồ thị mà đồ thị có hệ số góc bằng không được gọi là stationary points. Nói cách khác, điểm đứng yên tại đó f '(x) = 0.

Để tìm điểm đứng yên của một hàm số mà chúng ta phân biệt, chúng ta cần đặt đạo hàm bằng 0 và giải phương trình.

Thí dụ

Ta tìm các điểm đứng yên của hàm số f (x) = 2x ³ + 3x ² - 12x + 17

Thực hiện các bước sau:

First let us enter the function and plot its graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y)

MATLAB thực thi mã và trả về âm mưu sau:

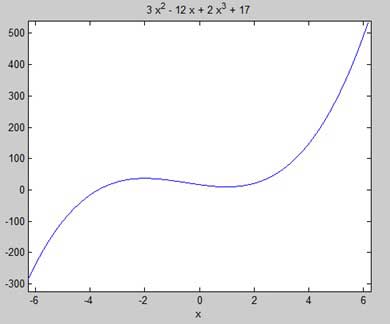
Đây là mã tương đương Octave cho ví dụ trên -

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
print -deps graph.eps

Our aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y, [-2, 2])

MATLAB thực thi mã và trả về âm mưu sau:

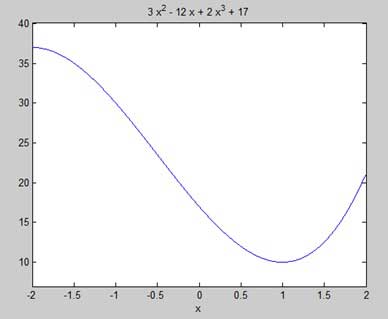
Đây là mã tương đương Octave cho ví dụ trên -

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

Next, let us compute the derivative.

g = diff(y)

MATLAB thực thi mã và trả về kết quả sau:

g =
   6*x^2 + 6*x - 12

Đây là Octave tương đương với phép tính ở trên -

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

Octave thực thi mã và trả về kết quả sau:

g =
   -12.0+(6.0)*x+(6.0)*x^(2.0)

Let us solve the derivative function, g, to get the values where it becomes zero.

s = solve(g)

MATLAB thực thi mã và trả về kết quả sau:

s =
   1
   -2

Sau đây là Octave tương đương với phép tính trên:

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

Octave thực thi mã và trả về kết quả sau:

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =

  -2
   1

This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. Chúng ta có thể thay thế một giá trị trong một hàm tượng trưng bằng cách sử dụng subs chỉ huy.

subs(y, 1), subs(y, -2)

MATLAB thực thi mã và trả về kết quả sau:

ans =
   10
ans =
   37

Sau đây là Octave tương đương với phép tính trên:

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)

ans =
   10.0
ans =
   37.0-4.6734207789940138748E-18*I

Do đó, giá trị nhỏ nhất và lớn nhất của hàm số f (x) = 2x ³ + 3x ² - 12x + 17, trong khoảng [-2,2] là 10 và 37.

Giải phương trình vi phân

MATLAB cung cấp dsolve lệnh để giải phương trình vi phân một cách ký hiệu.

Dạng cơ bản nhất của dsolve lệnh để tìm lời giải cho một phương trình là

dsolve('eqn')

trong đó eqn là một chuỗi văn bản được sử dụng để nhập phương trình.

Nó trả về một giải pháp tượng trưng với một tập hợp các hằng số tùy ý mà MATLAB dán nhãn C1, C2, v.v.

Bạn cũng có thể chỉ định điều kiện ban đầu và điều kiện biên cho vấn đề, dưới dạng danh sách được phân tách bằng dấu phẩy theo sau phương trình dưới dạng:

dsolve('eqn','cond1', 'cond2',…)

Với mục đích sử dụng lệnh dsolve, derivatives are indicated with a D. Ví dụ, một phương trình như f '(t) = -2 * f + cost (t) được nhập dưới dạng:

'Df = -2*f + cos(t)'

Các đạo hàm cấp cao hơn được biểu thị bằng cách theo sau D theo bậc của đạo hàm.

Ví dụ, phương trình f "(x) + 2f '(x) = 5sin3x nên được nhập dưới dạng:

'D2y + 2Dy = 5*sin(3*x)'

Chúng ta hãy lấy một ví dụ đơn giản về phương trình vi phân bậc nhất: y '= 5y.

s = dsolve('Dy = 5*y')

MATLAB thực thi mã và trả về kết quả sau:

s =
   C2*exp(5*t)

Chúng ta hãy lấy một ví dụ khác về phương trình vi phân bậc hai như: y "- y = 0, y (0) = -1, y '(0) = 2.

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

MATLAB thực thi mã và trả về kết quả sau:

ans =
   exp(t)/2 - (3*exp(-t))/2