MATLAB - Đồ họa

Chương này sẽ tiếp tục khám phá khả năng vẽ và đồ họa của MATLAB. Chúng ta sẽ thảo luận -

Vẽ biểu đồ thanh
Vẽ đường viền
Lô ba chiều

Vẽ biểu đồ thanh

Các barlệnh vẽ biểu đồ thanh hai chiều. Hãy để chúng tôi lấy một ví dụ để chứng minh ý tưởng.

Thí dụ

Hãy để chúng tôi có một lớp học tưởng tượng với 10 học sinh. Chúng tôi biết phần trăm số điểm mà những học sinh này đạt được là 75, 58, 90, 87, 50, 85, 92, 75, 60 và 95. Chúng tôi sẽ vẽ biểu đồ thanh cho dữ liệu này.

Tạo tệp kịch bản và nhập mã sau:

x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps

Khi bạn chạy tệp, MATLAB hiển thị biểu đồ thanh sau:

Vẽ đường viền

Đường đồng mức của một hàm hai biến là một đường cong mà hàm có giá trị không đổi. Đường đồng mức được sử dụng để tạo bản đồ đường đồng mức bằng cách nối các điểm có độ cao bằng nhau trên một mức nhất định, chẳng hạn như mực nước biển trung bình.

MATLAB cung cấp một contour chức năng vẽ bản đồ đường đồng mức.

Thí dụ

Hãy để chúng tôi tạo một bản đồ đường bao hiển thị các đường đồng mức cho một hàm đã cho g = f (x, y). Hàm này có hai biến. Vì vậy, chúng ta sẽ phải tạo ra hai biến độc lập, tức là hai tập dữ liệu x và y. Điều này được thực hiện bằng cách gọimeshgrid chỉ huy.

Các meshgrid lệnh được sử dụng để tạo một ma trận các phần tử cung cấp phạm vi trên x và y cùng với đặc điểm kỹ thuật của gia số trong từng trường hợp.

Hãy vẽ đồ thị hàm g = f (x, y), trong đó −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Chúng ta hãy lấy gia số 0,1 cho cả hai giá trị. Các biến được đặt là -

[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);

Cuối cùng, chúng ta cần gán chức năng. Cho hàm số của chúng ta là: x ² + y ²

Tạo tệp kịch bản và nhập mã sau:

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
contour(x,y,g)                         % call the contour function
print -deps graph.eps

Khi bạn chạy tệp, MATLAB hiển thị bản đồ đường viền sau:

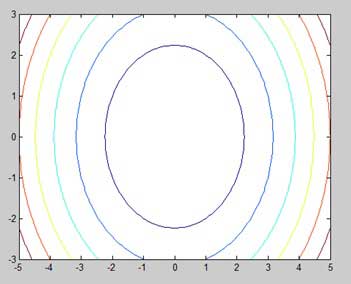
Hãy để chúng tôi sửa đổi mã một chút để chỉnh sửa bản đồ

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
[C, h] = contour(x,y,g);               % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.eps

Khi bạn chạy tệp, MATLAB hiển thị bản đồ đường viền sau:

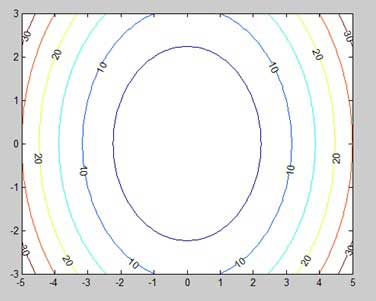
Ba lô chiều

Đồ thị ba chiều về cơ bản hiển thị một bề mặt được xác định bởi một hàm trong hai biến, g = f (x, y).

Như trước đây, để định nghĩa g, trước tiên chúng ta tạo một tập hợp (x, y) điểm trên miền của hàm bằng cách sử dụng meshgridchỉ huy. Tiếp theo, chúng tôi chỉ định chức năng cho chính nó. Cuối cùng, chúng tôi sử dụngsurf lệnh để tạo một biểu đồ bề mặt.

Ví dụ sau thể hiện khái niệm -

Thí dụ

Hãy để chúng tôi tạo một bản đồ bề mặt 3D cho hàm g = xe ^{- (x ² + y ² )}

Tạo tệp kịch bản và nhập mã sau:

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Khi bạn chạy tệp, MATLAB hiển thị bản đồ 3-D sau:

Bạn cũng có thể sử dụng meshlệnh tạo bề mặt ba chiều. Tuy nhiên,surf lệnh hiển thị cả các đường kết nối và các mặt của bề mặt bằng màu sắc, trong khi, mesh lệnh tạo một bề mặt khung dây với các đường màu nối các điểm xác định.