Volumen eines rechteckigen Prismas aus Einheitswürfeln
EIN unit cubehat eine Länge von 1 Einheit, eine Breite von 1 Einheit und eine Höhe von 1 Einheit. Sein Volumen beträgt 1 Kubikeinheit.
Jede feste Form kann als aus Einheitswürfeln hergestellt dargestellt werden. Das Zählen der Anzahl der Einheitswürfel in dieser festen Form ergibt das Volumen. Der grün schattierte Würfel ist ein Einheitswürfel.
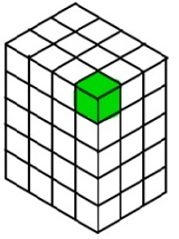
Definition des Volumens: Die Anzahl oder Menge der Kubikeinheiten, die zum Füllen eines definierten Raums erforderlich sind, wird als Volumen bezeichnet.
Formel für das Volumen eines rechteckigen Prismas
Das Volumen eines rechteckigen Prismas der Länge l, Breite w und Höhe h ergibt sich aus der Formel.
Das Volumen eines rechteckigen Prismas ergibt sich aus dem Produkt aus Länge, Breite und Höhe h des Prismas.
Volumen V = 1 × B × H Kubikeinheiten
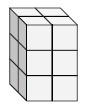
Finden Sie die Länge, Breite und Höhe des folgenden rechteckigen Prismas. Dann finden Sie die Lautstärke.
Lösung
Step 1:
Das gegebene Prisma hat eine Länge = 2; Breite = 3; Höhe = 2
Step 2:
Das Volumen des Prismas V = 1 × B × H.
= 2 × 3 × 2
= 12 kubische Einheiten.
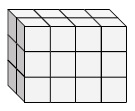
Finden Sie die Länge, Breite und Höhe des folgenden rechteckigen Prismas. Dann finden Sie die Lautstärke.
Lösung
Step 1:
Das gegebene Prisma hat eine Länge von 4; Breite = 3; Höhe = 2
Step 2:
Das Volumen des Prismas V = 1 × B × H.
= 4 × 3 × 2
= 24 kubische Einheiten.