Volumen eines Volumenkörpers aus Würfeln mit Kantenlängen in Einheitenfraktionen
Hier finden wir das Volumen der Feststoffe aus Würfeln mit Kantenlängen in Bruchteilen. Stellen Sie sich zum Beispiel einen Körper mit den Abmessungen 3 Zoll × 3 Zoll × 3 aus kleinen Würfeln mit Kantenlängen von $ \ frac {1} {2} $ Zoll vor.
In diesem Fall besteht der Körper aus 6 × 6 × 6 kleinen Würfeln mit Kantenlängen von $ \ frac {1} {2} $ inch. Das Volumen des Feststoffs wäre in diesem Fall also
Volume = lwh = $ 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} $
= 3 × 3 × 3 = 27 Kubikzoll
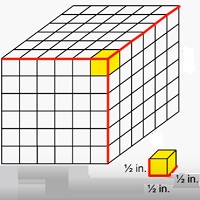
Formel für das Volumen des Feststoffs aus Würfeln mit einheitlichen Bruchkantenlängen
Angenommen, der Körper ist ein Würfel aus Kanteneinheiten
b = Anzahl der Würfel mit einer Einheitsbruchkantenlänge entlang jeder Kante
k = Einheitsbruchkantenlänge
Volume of solid = b × k × b × k × b × k cubic units
Ermitteln Sie das Volumen des folgenden Festkörpers aus Würfeln mit Kantenlängen in Bruchteilen. Jede Prismeneinheit wird in cm gemessen (nicht maßstabsgetreu)
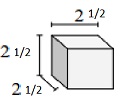
Lösung
Step 1:
Festkörper aus Würfeln mit Einheitsbruchkantenlängen von $ \ frac {1} {2} $ cm
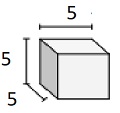
Step 2:
Volumen V = lwh = $ 2 \ frac {1} {2} \ mal 2 \ frac {1} {2} \ mal 2 \ frac {1} {2} $
= $ 5 \ times \ frac {1} {2} \ times 5 \ times \ frac {1} {2} \ times 5 \ times \ frac {1} {2} $
= $ 15 \ frac {5} {8} $ cu cm
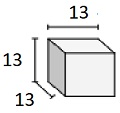
Ermitteln Sie das Volumen des folgenden Festkörpers aus Würfeln mit Kantenlängen in Bruchteilen. Jede Prismeneinheit wird in cm gemessen (nicht maßstabsgetreu)
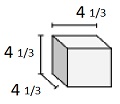
Lösung
Step 1:
Festkörper aus Würfeln mit Kantenlängen von $ \ frac {1} {3} $ cm
Step 2:
Volumen V = lwh = $ 4 \ frac {1} {3} \ mal 4 \ frac {1} {3} \ mal 4 \ frac {1} {3} $
= $ 13 \ times \ frac {1} {3} \ times 13 \ times \ frac {1} {3} \ times 13 \ times \ frac {1} {3} $
= $ 81 \ frac {10} {27} $ cu cm