Volumen des Dreiecksprismas
In dieser Lektion finden wir das Volumen eines dreieckigen Prismas
Ein dreieckiges Prisma ist ein Prisma mit zwei kongruenten parallelen Dreiecken als Basis und rechteckigen Seitenflächen.

Formula for the volume of a triangular prism
Wenn A die Fläche des Basisdreiecks und h die Höhe des Prismas ist, ist das Volumen des Prismas gegeben durch
Volumen V = A × h
Wobei A = $ \ frac {1} {2} $ bh oder $ \ sqrt {s (sa) (sb) (sc)} $ oder $ a ^ 2 \ sqrt {3} / 4 $
b ist die Basis des Dreiecks und h ist die Höhe
a, b und c sind die Seiten des Dreiecks und s = (a + b + c) / 2
a ist die Seite eines gleichseitigen Dreiecks
Finden Sie das Volumen des folgenden dreieckigen Prismas.
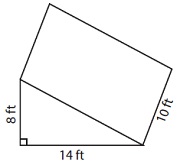
Lösung
Step 1:
Volumen eines dreieckigen Prismas = Bereiche des Basisdreiecks × Höhe des Prismas
Step 2:
Volumen des gegebenen Prismas V = $ \ frac {1} {2} $ × 14 × 8 × 10
= 560 Kubikfuß
Finden Sie das Volumen des folgenden dreieckigen Prismas.

Lösung
Step 1:
Volumen eines dreieckigen Prismas = Bereiche des Basisdreiecks × Höhe des Prismas
Step 2:
Volumen des gegebenen Prismas V = $ \ frac {1} {2} $ × 14 × 8 × 6
= 336 Kubikfuß