Fuzzy Logic - Mengenlehre
Fuzzy-Mengen können als Erweiterung und grobe Vereinfachung klassischer Mengen betrachtet werden. Dies kann am besten im Zusammenhang mit der festgelegten Mitgliedschaft verstanden werden. Grundsätzlich erlaubt es eine teilweise Mitgliedschaft, was bedeutet, dass es Elemente enthält, die unterschiedliche Zugehörigkeitsgrade in der Menge haben. Daraus können wir den Unterschied zwischen klassischer Menge und Fuzzy-Menge verstehen. Die klassische Menge enthält Elemente, die genaue Eigenschaften der Mitgliedschaft erfüllen, während die Fuzzy-Menge Elemente enthält, die ungenaue Eigenschaften der Mitgliedschaft erfüllen.

Mathematisches Konzept
Eine Fuzzy-Menge $ \ widetilde {A} $ im Informationsuniversum $ U $ kann als eine Menge geordneter Paare definiert und mathematisch dargestellt werden als -
$$ \ widetilde {A} = \ left \ {\ left (y, \ mu _ {\ widetilde {A}} \ left (y \ right) \ right) | y \ in U \ right \} $$
Hier nimmt $ \ mu _ {\ widetilde {A}} \ left (y \ right) $ = Zugehörigkeitsgrad von $ y $ in \ widetilde {A} Werte im Bereich von 0 bis 1 an, dh $ \ mu _ {\ widetilde {A}} (y) \ in \ left [0,1 \ right] $.
Darstellung der Fuzzy-Menge
Betrachten wir nun zwei Fälle von Informationsuniversum und verstehen, wie eine Fuzzy-Menge dargestellt werden kann.
Fall 1
Wenn das Informationsuniversum $ U $ diskret und endlich ist -
$$ \ widetilde {A} = \ left \ {\ frac {\ mu _ {\ widetilde {A}} \ left (y_1 \ right)} {y_1} + \ frac {\ mu _ {\ widetilde {A}} \ left (y_2 \ right)} {y_2} + \ frac {\ mu _ {\ widetilde {A}} \ left (y_3 \ right)} {y_3} + ... \ right \} $$
$ = \ left \ {\ sum_ {i = 1} ^ {n} \ frac {\ mu _ {\ widetilde {A}} \ left (y_i \ right)} {y_i} \ right \} $
Fall 2
Wenn das Informationsuniversum $ U $ kontinuierlich und unendlich ist -
$$ \ widetilde {A} = \ left \ {\ int \ frac {\ mu _ {\ widetilde {A}} \ left (y \ right)} {y} \ right \} $$
In der obigen Darstellung repräsentiert das Summationssymbol die Sammlung jedes Elements.
Operationen an Fuzzy-Sets
Mit zwei Fuzzy-Mengen $ \ widetilde {A} $ und $ \ widetilde {B} $, dem Informationsuniversum $ U $ und einem Element des Universums drücken die folgenden Beziehungen die Vereinigung, Schnittmenge und Komplementoperation auf Fuzzy-Mengen aus.
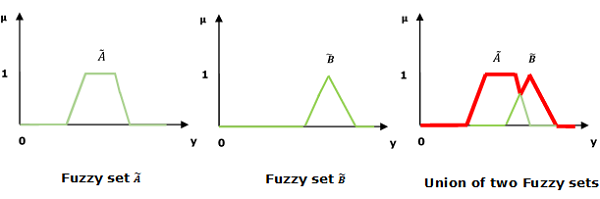
Union / Fuzzy 'OR'
Betrachten wir die folgende Darstellung, um zu verstehen, wie die Union/Fuzzy ‘OR’ Beziehung funktioniert -
$$ \ mu _ {{\ widetilde {A} \ cup \ widetilde {B}}} \ left (y \ right) = \ mu _ {\ widetilde {A}} \ vee \ mu _ \ widetilde {B} \ quad \ forall y \ in U $$
Hier steht ∨ für die 'max'-Operation.
Kreuzung / Fuzzy 'UND'
Betrachten wir die folgende Darstellung, um zu verstehen, wie die Intersection/Fuzzy ‘AND’ Beziehung funktioniert -
$$ \ mu _ {{\ widetilde {A} \ cap \ widetilde {B}}} \ left (y \ right) = \ mu _ {\ widetilde {A}} \ wedge \ mu _ \ widetilde {B} \ quad \ forall y \ in U $$
Hier steht ∧ für die 'min'-Operation.

Komplement / Fuzzy 'NICHT'
Betrachten wir die folgende Darstellung, um zu verstehen, wie die Complement/Fuzzy ‘NOT’ Beziehung funktioniert -
$$ \ mu _ {\ widetilde {A}} = 1- \ mu _ {\ widetilde {A}} \ left (y \ right) \ quad y \ in U $$

Eigenschaften von Fuzzy-Mengen
Lassen Sie uns die verschiedenen Eigenschaften von Fuzzy-Mengen diskutieren.
Kommutativgesetz
Mit zwei Fuzzy-Mengen $ \ widetilde {A} $ und $ \ widetilde {B} $ heißt es in dieser Eigenschaft:
$$ \ widetilde {A} \ cup \ widetilde {B} = \ widetilde {B} \ cup \ widetilde {A} $$
$$ \ widetilde {A} \ cap \ widetilde {B} = \ widetilde {B} \ cap \ widetilde {A} $$
Assoziatives Eigentum
Mit drei Fuzzy-Mengen $ \ widetilde {A} $, $ \ widetilde {B} $ und $ \ widetilde {C} $ heißt es in dieser Eigenschaft:
$$ (\ widetilde {A} \ cup \ left \ widetilde {B}) \ cup \ widetilde {C} \ right = \ left \ widetilde {A} \ cup (\ widetilde {B} \ right) \ cup \ widetilde {C}) $$
$$ (\ widetilde {A} \ cap \ left \ widetilde {B}) \ cap \ widetilde {C} \ right = \ left \ widetilde {A} \ cup (\ widetilde {B} \ right \ cap \ widetilde { C}) $$
Verteilungseigenschaft
Mit drei Fuzzy-Mengen $ \ widetilde {A} $, $ \ widetilde {B} $ und $ \ widetilde {C} $ heißt es in dieser Eigenschaft:
$$ \ widetilde {A} \ cup \ left (\ widetilde {B} \ cap \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cup \ widetilde {B} \ right) \ cap \ left (\ widetilde {A} \ cup \ widetilde {C} \ right) $$
$$ \ widetilde {A} \ cap \ left (\ widetilde {B} \ cup \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cap \ widetilde {B} \ right) \ cup \ left (\ widetilde {A} \ cap \ widetilde {C} \ right) $$
Idempotenz-Eigenschaft
Für jede Fuzzy-Menge $ \ widetilde {A} $ gibt diese Eigenschaft an:
$$ \ widetilde {A} \ cup \ widetilde {A} = \ widetilde {A} $$
$$ \ widetilde {A} \ cap \ widetilde {A} = \ widetilde {A} $$
Identitätseigenschaft
Für die Fuzzy-Menge $ \ widetilde {A} $ und die universelle Menge $ U $ lautet diese Eigenschaft:
$$ \ widetilde {A} \ cup \ varphi = \ widetilde {A} $$
$$ \ widetilde {A} \ cap U = \ widetilde {A} $$
$$ \ widetilde {A} \ cap \ varphi = \ varphi $$
$$ \ widetilde {A} \ cup U = U $$
Transitive Eigenschaft
Mit drei Fuzzy-Mengen $ \ widetilde {A} $, $ \ widetilde {B} $ und $ \ widetilde {C} $ heißt es in dieser Eigenschaft:
$$ Wenn \: \ widetilde {A} \ subseteq \ widetilde {B} \ subseteq \ widetilde {C}, \: dann \: \ widetilde {A} \ subseteq \ widetilde {C} $$
Involution-Eigenschaft
Für jede Fuzzy-Menge $ \ widetilde {A} $ gibt diese Eigenschaft an:
$$ \ overline {\ overline {\ widetilde {A}}} = \ widetilde {A} $$
De Morgans Gesetz
Dieses Gesetz spielt eine entscheidende Rolle beim Nachweis von Tautologien und Widersprüchen. Dieses Gesetz besagt -
$$ \ overline {{\ widetilde {A} \ cap \ widetilde {B}}} = \ overline {\ widetilde {A}} \ cup \ overline {\ widetilde {B}} $$
$$ \ overline {{\ widetilde {A} \ cup \ widetilde {B}}} = \ overline {\ widetilde {A}} \ cap \ overline {\ widetilde {B}} $$