Graphentheorie - Konnektivität
Ob es möglich ist, einen Graphen von einem Scheitelpunkt zum anderen zu durchlaufen, hängt davon ab, wie ein Graph verbunden ist. Konnektivität ist ein Grundkonzept in der Graphentheorie. Konnektivität definiert, ob ein Diagramm verbunden oder nicht verbunden ist. Es verfügt über Unterthemen, die auf Kante und Scheitelpunkt basieren und als Kantenkonnektivität und Scheitelpunktkonnektivität bezeichnet werden. Lassen Sie uns sie im Detail diskutieren.
Konnektivität
Ein Graph soll sein connected if there is a path between every pair of vertex. Von jedem Scheitelpunkt zu jedem anderen Scheitelpunkt sollte es einen Pfad zum Überqueren geben. Das nennt man die Konnektivität eines Graphen. Ein Diagramm mit mehreren getrennten Eckpunkten und Kanten wird als getrennt bezeichnet.
Example 1
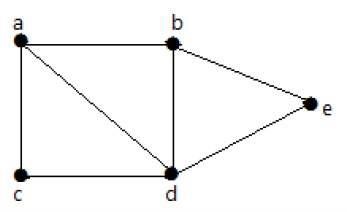
In der folgenden Grafik ist es möglich, von einem Scheitelpunkt zu einem anderen Scheitelpunkt zu reisen. Zum Beispiel kann man über den Pfad 'ab-e' vom Scheitelpunkt 'a' zum Scheitelpunkt 'e' wechseln.
Example 2
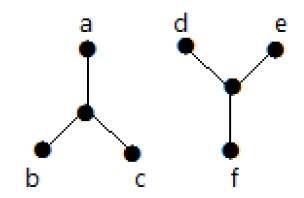
Im folgenden Beispiel ist das Überqueren von Scheitelpunkt 'a' zu Scheitelpunkt 'f' nicht möglich, da zwischen ihnen weder direkt noch indirekt ein Pfad besteht. Daher ist es ein nicht verbundener Graph.
Scheitelpunkt schneiden
Sei 'G' ein zusammenhängender Graph. Ein Scheitelpunkt V ∈ G wird als Schnittscheitelpunkt von 'G' bezeichnet, wenn 'G-V' (Löschen von 'V' aus 'G') zu einem nicht verbundenen Graphen führt. Durch Entfernen eines Schnittscheitelpunkts aus einem Diagramm wird dieser in zwei oder mehr Diagramme unterteilt.
Note - Durch Entfernen eines Schnittscheitelpunkts wird möglicherweise ein Diagramm getrennt.
Ein verbundener Graph 'G' darf höchstens (n - 2) Eckpunkte schneiden.
Example
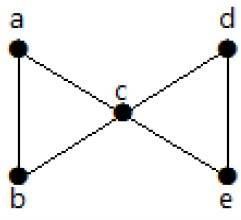
In der folgenden Grafik sind die Eckpunkte 'e' und 'c' die geschnittenen Eckpunkte.

Durch Entfernen von 'e' oder 'c' wird das Diagramm zu einem nicht verbundenen Diagramm.

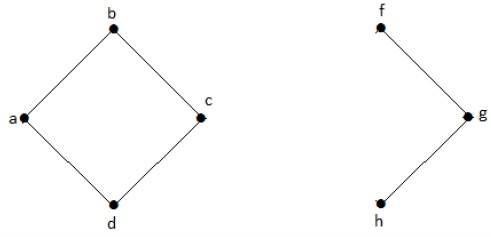
Ohne 'g' gibt es keinen Pfad zwischen dem Scheitelpunkt 'c' und dem Scheitelpunkt 'h' und vielen anderen. Daher ist es ein nicht verbundener Graph mit einem Schnittscheitelpunkt als 'e'. In ähnlicher Weise ist 'c' auch ein Schnittpunkt für das obige Diagramm.
Schnittkante (Brücke)
Sei 'G' ein zusammenhängender Graph. Eine Kante 'e' ∈ G wird als Schnittkante bezeichnet, wenn 'G-e' zu einem nicht verbundenen Graphen führt.
Wenn das Entfernen einer Kante in einem Diagramm zu zwei oder mehr Diagrammen führt, wird diese Kante als Schnittkante bezeichnet.
Example
In der folgenden Grafik ist die Schnittkante [(c, e)].

Durch Entfernen der Kante (c, e) aus dem Diagramm wird ein nicht verbundenes Diagramm.


In der obigen Grafik wird durch Entfernen der Kante (c, e) die Grafik in zwei Teile geteilt, was nichts anderes als eine nicht verbundene Grafik ist. Daher ist die Kante (c, e) eine Schnittkante des Graphen.
Note - Sei 'G' ein zusammenhängender Graph mit 'n' Eckpunkten
eine Schnittkante e ∈ G genau dann, wenn die Kante 'e' nicht Teil eines Zyklus in G ist.
Die maximal mögliche Anzahl von Schnittkanten ist 'n-1'.
Wenn Schnittkanten vorhanden sind, sind auch Schnittscheitelpunkte vorhanden, da mindestens ein Scheitelpunkt einer Schnittkante ein Schnittscheitelpunkt ist.
Wenn ein Schnittscheitelpunkt vorhanden ist, kann eine Schnittkante vorhanden sein oder nicht.
Satz eines Graphen ausschneiden
Sei 'G' = (V, E) ein zusammenhängender Graph. Eine Teilmenge E 'von E wird als Schnittmenge von G bezeichnet, wenn durch Löschen aller Kanten von E' aus G G getrennt wird.
Wenn durch das Löschen einer bestimmten Anzahl von Kanten aus einem Diagramm die Verbindung getrennt wird, werden diese gelöschten Kanten als Schnittmenge des Diagramms bezeichnet.
Example
Schauen Sie sich die folgende Grafik an. Sein Schnittsatz ist E1 = {e1, e3, e5, e8}.
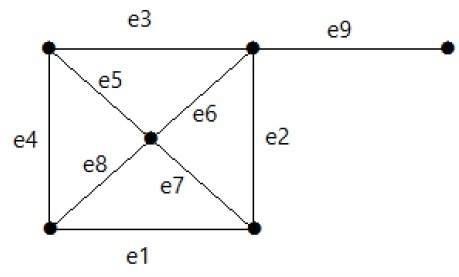
Nach dem Entfernen des Schnittsatzes E1 aus dem Diagramm sieht es wie folgt aus:
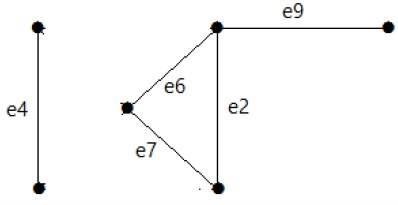
Ebenso gibt es andere Schnittsätze, die das Diagramm trennen können -
E3 = {e9} - Kleinster Schnittsatz des Diagramms.
E4 = {e3, e4, e5}
Edge-Konnektivität
Sei 'G' ein zusammenhängender Graph. Die minimale Anzahl von Kanten, deren Entfernung 'G' trennt, wird als Kantenkonnektivität von G bezeichnet.
Notation - λ (G)
Mit anderen Worten, die number of edges in a smallest cut set of G wird die Kantenkonnektivität von G genannt.
Wenn 'G' eine Schnittkante hat, ist λ (G) 1. (Kantenkonnektivität von G.)
Example
Schauen Sie sich die folgende Grafik an. Durch Entfernen von zwei minimalen Kanten wird der verbundene Graph getrennt. Daher beträgt seine Kantenkonnektivität (λ (G)) 2.
Hier sind die vier Möglichkeiten, das Diagramm durch Entfernen von zwei Kanten zu trennen:

Vertex-Konnektivität
Sei 'G' ein zusammenhängender Graph. Die minimale Anzahl von Scheitelpunkten, deren Entfernung 'G' entweder trennt oder 'G' in einen trivialen Graphen reduziert, wird als Scheitelpunktkonnektivität bezeichnet.
Notation - K (G)
Example
Wenn Sie im obigen Diagramm die Eckpunkte 'e' und 'i' entfernen, wird das Diagramm getrennt.

Wenn G einen Schnittscheitelpunkt hat, ist K (G) = 1.
Notation - Für jeden verbundenen Graphen G,
K (G) ≤ λ (G) ≤ δ (G)
Scheitelpunktkonnektivität (K (G)), Kantenkonnektivität (λ (G)), Mindestanzahl von G-Graden (δ (G)).
Example
Berechnen Sie λ (G) und K (G) für das folgende Diagramm -
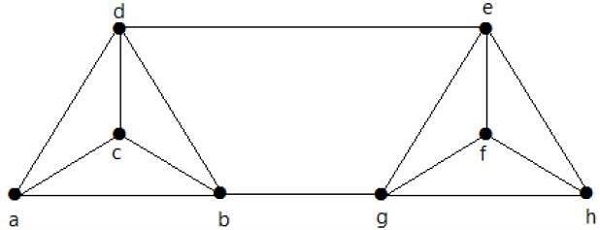
Solution
Aus der Grafik,
δ (G) = 3
K (G) ≤ λ (G) ≤ δ (G) = 3 (1)
K (G) ≥ 2 (2)
Durch Löschen der Kanten {d, e} und {b, h} können wir G trennen.
Deshalb,
λ (G) = 2
2 ≤ λ (G) ≤ δ (G) = 2 (3)
Aus (2) und (3) ergibt sich die Scheitelpunktkonnektivität K (G) = 2