Graphentheorie - Übereinstimmungen
Ein übereinstimmender Graph ist ein Untergraph eines Graphen, bei dem keine Kanten nebeneinander liegen. Es sollte einfach keinen gemeinsamen Scheitelpunkt zwischen zwei Kanten geben.
Matching
Sei 'G' = (V, E) ein Graph. Ein Untergraph heißt passendes M (G),if each vertex of G is incident with at most one edge in Mdh
Grad (V) ≤ 1 ≤ V ≤ G.
was bedeutet, dass in dem übereinstimmenden Graphen M (G) die Eckpunkte einen Grad von 1 oder 0 haben sollten, wobei die Kanten vom Graphen G einfallen sollten.
Notation - M (G)
Example
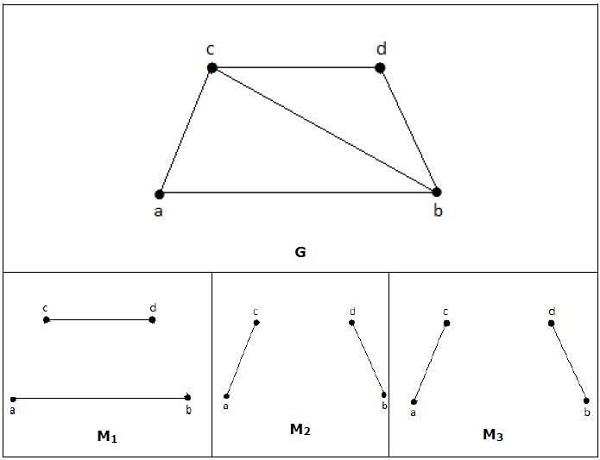

In einem Matching,
Wenn deg (V) = 1 ist, wird (V) als übereinstimmend bezeichnet
Wenn deg (V) = 0 ist, stimmt (V) nicht überein.
Bei einem Matching sind keine zwei Kanten benachbart. Dies liegt daran, dass, wenn zwei Kanten benachbart sind, der Grad des Scheitelpunkts, der diese beiden Kanten verbindet, einen Grad von 2 hat, der gegen die Übereinstimmungsregel verstößt.
Maximale Übereinstimmung
Ein übereinstimmendes M des Graphen 'G' wird als maximal bezeichnet if no other edges of ‘G’ can be added to M.
Example

M1, M2, M3 aus dem obigen Diagramm sind die maximale Übereinstimmung von G.
Maximale Übereinstimmung
Es ist auch als größte maximale Übereinstimmung bekannt. Die maximale Übereinstimmung ist definiert als die maximale Übereinstimmung mit der maximalen Anzahl von Kanten.
Die Anzahl der Kanten in der maximalen Übereinstimmung von 'G' wird als its bezeichnet matching number.
Example
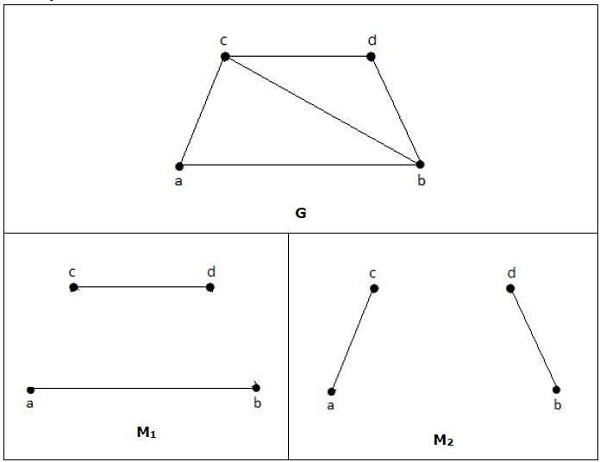
Für einen im obigen Beispiel angegebenen Graphen sind M1 und M2 die maximale Übereinstimmung von 'G' und seine Übereinstimmungszahl ist 2. Daher können wir unter Verwendung des Graphen G nur die Teilgraphen mit maximal 2 Kanten bilden. Daher haben wir die übereinstimmende Nummer als zwei.
Perfekte Übereinstimmung
Eine Übereinstimmung (M) des Graphen (G) wird als perfekte Übereinstimmung bezeichnet, wenn jeder Scheitelpunkt des Graphen g (G) auf genau eine Kante der Übereinstimmung (M) fällt, dh
Grad (V) = 1 ≤ V.
Der Grad jedes einzelnen Scheitelpunkts im Untergraphen sollte einen Grad von 1 haben.
Example
In den folgenden Diagrammen sind M1 und M2 Beispiele für die perfekte Übereinstimmung von G.
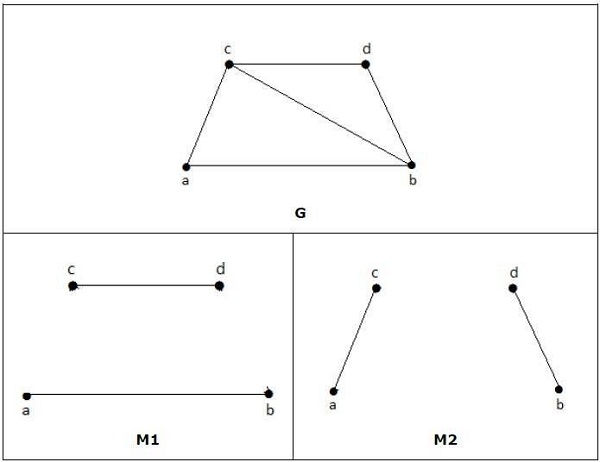
Note - Jede perfekte Übereinstimmung des Diagramms ist auch eine maximale Übereinstimmung des Diagramms, da keine Chance besteht, eine weitere Kante in ein perfekt übereinstimmendes Diagramm einzufügen.
Eine maximale Übereinstimmung des Diagramms muss nicht perfekt sein. Wenn ein Graph 'G' perfekt übereinstimmt, dann die Anzahl der Eckpunkte | V (G) | ist gerade. Wenn es ungerade ist, paart sich der letzte Scheitelpunkt mit dem anderen Scheitelpunkt, und schließlich bleibt ein einzelner Scheitelpunkt übrig, der nicht mit einem anderen Scheitelpunkt gepaart werden kann, für den der Grad Null ist. Es verstößt eindeutig gegen das perfekte Matching-Prinzip.
Example
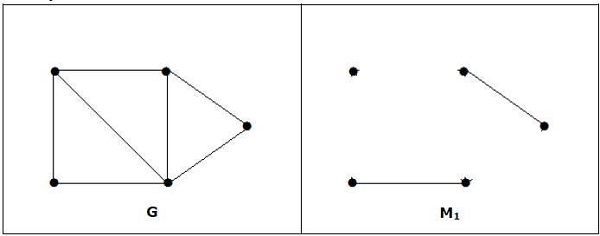
Note- Die Umkehrung der obigen Aussage muss nicht wahr sein. Wenn G eine gerade Anzahl von Eckpunkten hat, muss M1 nicht perfekt sein.
Example
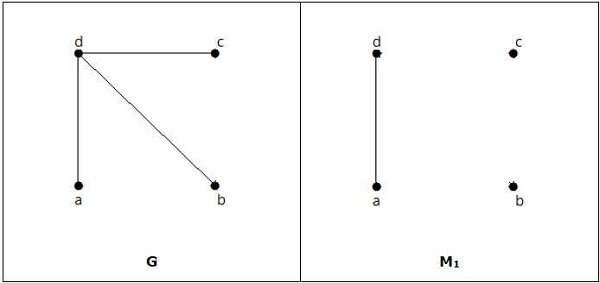
Es stimmt überein, aber es ist keine perfekte Übereinstimmung, obwohl es eine gerade Anzahl von Eckpunkten hat.