Graphentheorie - Beispiele
In diesem Kapitel werden einige Standardbeispiele behandelt, um die Konzepte zu demonstrieren, die wir bereits in den vorherigen Kapiteln erörtert haben.
Beispiel 1
Find the number of spanning trees in the following graph.
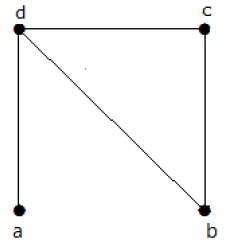
Lösung
Die Anzahl der Spannbäume, die aus dem obigen Diagramm erhalten wurden, beträgt 3. Sie sind wie folgt:
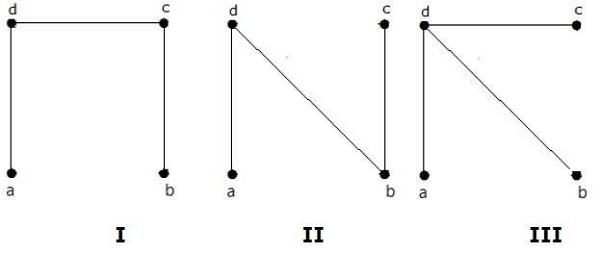
Diese drei sind die Spannbäume für die angegebenen Diagramme. Hier sind die Graphen I und II isomorph zueinander. Es ist klar, dass die Anzahl der nicht isomorphen Spannbäume zwei beträgt.
Beispiel 2
How many simple non-isomorphic graphs are possible with 3 vertices?
Lösung
Es sind 4 nicht-isomorphe Graphen mit 3 Eckpunkten möglich. Sie sind unten gezeigt.
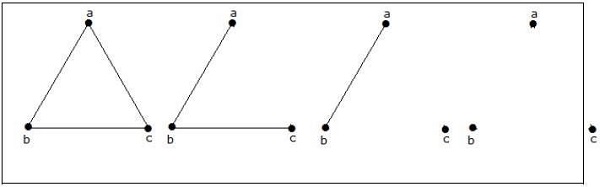
Beispiel 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
Lösung
Durch die Summe der Gradsätze,
20 Σ i = 1 Grad (Vi) = 2 | E |
20 (3) = 2 | E |
| E | = 30
Nach Eulers Formel
| V | + | R | = | E | + 2
20+ | R | = 30 + 2
| R | = 12
Daher beträgt die Anzahl der Regionen 12.
Beispiel 4
What is the chromatic number of complete graph Kn?
Lösung
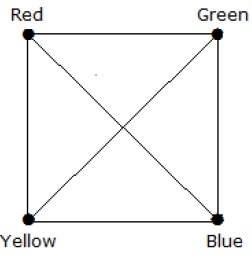
In einem vollständigen Diagramm grenzt jeder Scheitelpunkt an die verbleibenden (n - 1) Scheitelpunkte. Daher benötigt jeder Scheitelpunkt eine neue Farbe. Daher ist die chromatische Zahl K n = n.
Beispiel 5
What is the matching number for the following graph?
Lösung
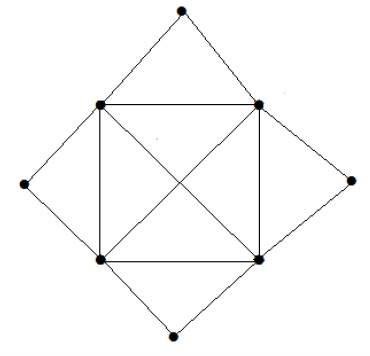
Anzahl der Eckpunkte = 9
Wir können nur 8 Eckpunkte abgleichen.
Übereinstimmende Nummer ist 4.
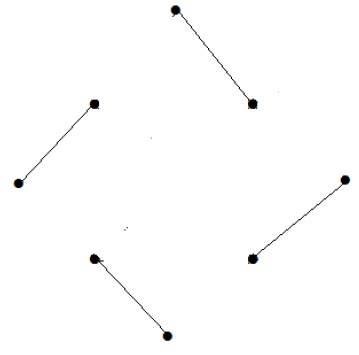
Beispiel 6
What is the line covering number of for the following graph?
Lösung
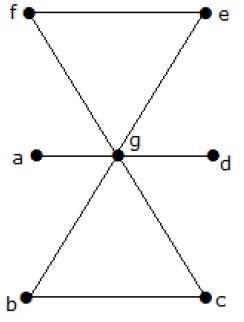
Anzahl der Eckpunkte = | V | = n = 7
Linienabdeckungszahl = (α 1 ) ≥ [n / 2] = 3
α 1 ≥ 3
Durch die Verwendung von 3 Kanten können wir alle Eckpunkte abdecken.
Daher ist die Zeilenabdeckungsnummer 3.