Graphentheorie - Durchquerbarkeit
Ein Diagramm kann durchlaufen werden, wenn Sie einen Pfad zwischen allen Scheitelpunkten zeichnen können, ohne denselben Pfad zurückzuverfolgen. Basierend auf diesem Pfad gibt es einige Kategorien wie den Euler-Pfad und die Euler-Schaltung, die in diesem Kapitel beschrieben werden.
Eulers Weg
Der Pfad eines Eulers enthält jede Kante von 'G' genau einmal und jeden Scheitelpunkt von 'G' mindestens einmal. Ein verbundener Graph G wird als durchlaufbar bezeichnet, wenn er einen Euler-Pfad enthält.
Example
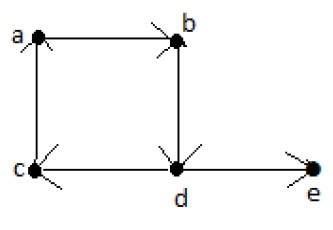
Eulers Pfad = dcabde.
Eulers Schaltung
Wenn im Euler-Pfad der Startscheitelpunkt mit dem Endscheitelpunkt identisch ist, wird er als Euler-Schaltung bezeichnet.
Example
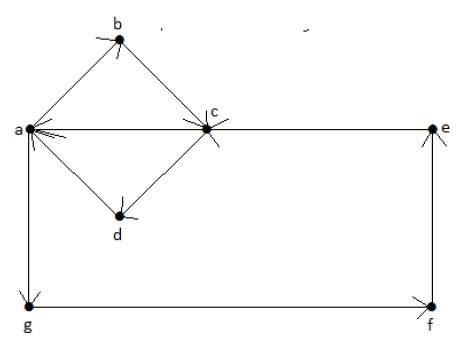
Euler’s Path = abcdagfeca.
Eulers Schaltungssatz
Ein verbundener Graph 'G' ist genau dann durchlaufbar, wenn die Anzahl der Eckpunkte mit ungeradem Grad in G genau 2 oder 0 beträgt. Ein verbundener Graph G kann einen Euler-Pfad enthalten, aber keine Euler-Schaltung, wenn er genau zwei Eckpunkte mit hat ein seltsamer Grad.
Note - Dieser Euler-Pfad beginnt mit einem Scheitelpunkt ungeraden Grades und endet mit dem anderen Scheitelpunkt ungeraden Grades.
Example
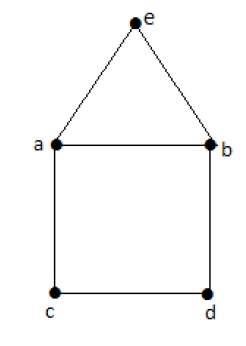
Euler’s Path- beabdca ist keine Euler-Schaltung, aber es ist ein Euler-Pfad. Es hat eindeutig genau 2 Eckpunkte ungeraden Grades.
Note - Wenn in einem verbundenen Graphen G die Anzahl der Eckpunkte mit ungeradem Grad = 0 ist, existiert die Euler-Schaltung.
Hamilton-Graph
Ein verbundener Graph G wird als Hamilton-Graph bezeichnet, wenn ein Zyklus existiert, der alle Eckpunkte von G enthält.
Jeder Zyklus ist eine Schaltung, aber eine Schaltung kann mehrere Zyklen enthalten. Ein solcher Zyklus heißt aHamiltonian cycle von G.
Hamilton-Pfad
Ein verbundener Graph wird als Hamilton-Graph bezeichnet, wenn er jeden Scheitelpunkt von G genau einmal enthält. Ein solcher Weg heißt aHamiltonian path.
Example
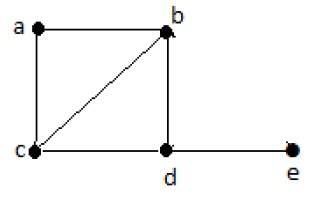
Hamiltonian Path- edbac.
Note
Die Euler-Schaltung enthält jede Kante des Graphen genau einmal.
In einem Hamilton-Zyklus können einige Kanten des Diagramms übersprungen werden.
Example
Schauen Sie sich die folgende Grafik an -
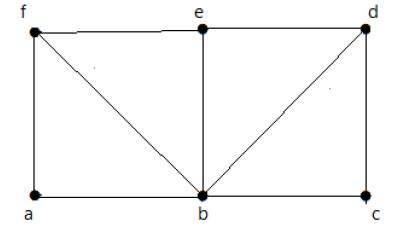
Für die oben gezeigte Grafik -
Euler-Pfad existiert - falsch
Euler-Schaltung existiert - falsch
Hamilton-Zyklus existiert - wahr
Hamilton-Pfad existiert - wahr
G hat vier Eckpunkte mit ungeradem Grad, daher ist es nicht überfahrbar. Durch Überspringen der Innenkanten hat der Graph einen Hamilton-Zyklus, der alle Eckpunkte durchläuft.