Graphentheorie - Bedeckungen
Ein Abdeckungsgraph ist ein Untergraph, der entweder alle Eckpunkte oder alle Kanten enthält, die einem anderen Graphen entsprechen. Ein Untergraph, der alle Eckpunkte enthält, heißt aline/edge covering. Ein Untergraph, der alle Kanten enthält, heißt avertex covering.
Linienabdeckung
Sei G = (V, E) ein Graph. Eine Teilmenge C (E) wird als Linienbedeckung von G bezeichnet, wenn jeder Scheitelpunkt von G mit mindestens einer Kante in C einfällt, d. H.
Grad (V) ≥ 1 ≤ V ≤ G.
weil jeder Scheitelpunkt durch eine Kante mit einem anderen Scheitelpunkt verbunden ist. Daher hat es einen Mindestgrad von 1.
Example
Schauen Sie sich die folgende Grafik an -
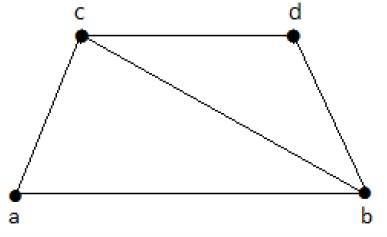
Seine Untergraphen mit Linienbedeckung sind wie folgt:
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
Die Linienbedeckung von 'G' existiert nicht genau dann, wenn 'G' einen isolierten Scheitelpunkt hat. Die Linienbedeckung eines Graphen mit 'n' Eckpunkten hat mindestens [n / 2] Kanten.
Minimale Linienbedeckung
Eine Linie, die C eines Graphen G abdeckt, soll minimal sein if no edge can be deleted from C.
Example
In der obigen Grafik sind die Untergraphen mit Linienbedeckung wie folgt:
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
Hier sind C 1 , C 2 , C 3 minimale Linienbedeckungen, während C 4 nicht daran liegt, dass wir {b, c} löschen können.
Minimale Leitungsabdeckung
Es ist auch bekannt als Smallest Minimal Line Covering. Eine minimale Linienbedeckung mit einer minimalen Anzahl von Kanten wird als minimale Linienbedeckung von 'G' bezeichnet. Die Anzahl der Kanten in einer minimalen Linienabdeckung in 'G' wird als bezeichnetline covering numbervon 'G' (α 1 ).
Example
Im obigen Beispiel sind C 1 und C 2 die minimale Linienbedeckung von G und α 1 = 2.
Jede Linienbedeckung enthält eine minimale Linienbedeckung.
Jede Linienbedeckung enthält keine minimale Linienbedeckung (C 3 enthält keine minimale Linienbedeckung.
Keine minimale Linienbedeckung enthält einen Zyklus.
Wenn eine Linie, die 'C' abdeckt, keine Pfade mit einer Länge von 3 oder mehr enthält, ist 'C' eine minimale Linienabdeckung, da alle Komponenten von 'C' Sterngraphen sind und aus einem Sterngraphen keine Kante gelöscht werden kann.
Scheitelpunktabdeckung
Sei 'G' = (V, E) ein Graph. Eine Teilmenge K von V wird als Scheitelpunktabdeckung von 'G' bezeichnet, wenn jede Kante von 'G' mit einem Scheitelpunkt in 'K' zusammenfällt oder von diesem abgedeckt wird.
Example
Schauen Sie sich die folgende Grafik an -
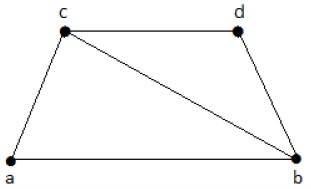
Die Untergraphen, die aus dem obigen Diagramm abgeleitet werden können, sind wie folgt:
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
K 4 = {a, d}
Hier haben K 1 , K 2 und K 3 eine Scheitelpunktbedeckung, während K 4 keine Scheitelpunktbedeckung hat, da es die Kante {bc} nicht bedeckt.
Minimale Scheitelpunktabdeckung
Ein Scheitelpunkt 'K' des Graphen 'G' wird als minimale Scheitelpunktabdeckung bezeichnet, wenn kein Scheitelpunkt aus 'K' gelöscht werden kann.
Example
In der obigen Grafik sind die Untergraphen mit Scheitelpunktbedeckung wie folgt:
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
Hier sind K 1 und K 2 minimale Scheitelpunktbedeckungen, während in K 3 der Scheitelpunkt 'd' gelöscht werden kann.
Minimale Scheitelpunktabdeckung
Es ist auch als kleinste minimale Scheitelpunktbedeckung bekannt. Eine minimale Scheitelpunktabdeckung des Graphen 'G' mit einer minimalen Anzahl von Scheitelpunkten wird als minimale Scheitelpunktabdeckung bezeichnet.
Die Anzahl der Scheitelpunkte in einer minimalen Scheitelpunktabdeckung von 'G' wird als Scheitelpunktabdeckungszahl von G (α 2 ) bezeichnet.
Example
In der folgenden Grafik sind die Untergraphen mit Scheitelpunktabdeckung wie folgt:
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}

Hier ist K 1 eine minimale Scheitelpunktabdeckung von G, da es nur zwei Scheitelpunkte hat. α 2 = 2.