Fläche eines Dreiecks

Einführung

Betrachten Sie ein Dreieck wie folgt

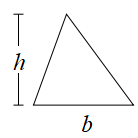
Wir können ein Rechteck wie folgt um das Dreieck zeichnen, so dass seine Länge b und seine Breite h ist.

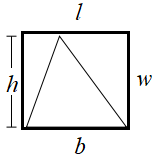
Wir bewegen uns um Dreiecke, um ein Parallelogramm zu bilden, dessen gegebenes Dreieck genau die Hälfte der Fläche hat. Die Fläche des Parallelogramms und des Rechtecks ist gleich.

Damit,

Dreiecksfläche = $ \ frac {1} {2} $ Rechteckfläche = $ \ frac {1} {2} $ l × w = $ \ frac {1} {2} $ b × h

Beispiel 1:

Suchen Sie den unten angegebenen Bereich des Dreiecks.

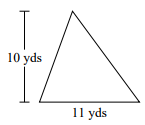
Lösung

Step 1:

Fläche des rechten Dreiecks = $ \ frac {1} {2} $ × b × h; b = Basis = 11 yd; h = Höhe = 10 m

Step 2:

Fläche des rechten Dreiecks = $ \ frac {1} {2} $ × 11 × 10 = 55 Quadratmeter.

Beispiel 2:

Suchen Sie den unten angegebenen Bereich des Dreiecks.

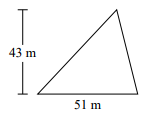
Lösung

Step 1:

Fläche des rechten Dreiecks = $ \ frac {1} {2} $ × b × h; b = Basis = 51 m; h = Höhe = 43 m

Step 2:

Fläche des rechten Dreiecks = $ \ frac {1} {2} $ × 51 × 43 = 1096,5 Quadratmeter.