Ermitteln der Fläche eines Trapezes in einem Raster mithilfe von Dreiecken und Rechtecken
In dieser Lektion finden wir Trapezoide auf Gittern, indem wir Dreiecke und Rechtecke verwenden. Die Trapezoide werden in Dreiecke und Rechtecke zerlegt und ihre Flächen gefunden. Die Summe dieser Flächen ergibt die Fläche des Trapezes auf dem Gitter.
Wir kennen die Fläche eines Dreiecks = $ \ frac {1} {2} $ b × h und
Fläche eines Rechtecks = l × w
Suchen Sie den Bereich des folgenden Trapezes mithilfe von Dreiecken und Rechtecken.
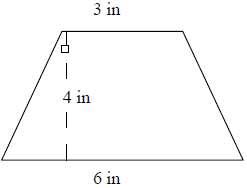
Lösung
Step 1:
Fläche des rechten Dreiecks = $ \ frac {1} {2} $ × b × h; b = Basis; h = Höhe.
Fläche von 2 rechtwinkligen Dreiecken = 2 × $ \ frac {1} {2} $ × b × h = 1,5 × 4 = 6 Quadratzoll.
Step 2:
Fläche des Rechtecks = l × w = 4 × 3 = 12 Quadratzoll
Step 3:
Fläche des Trapezes = Fläche der Dreiecke + Fläche des Rechtecks
= 6 + 12
= 18 Quadratmeter
Suchen Sie den Bereich des folgenden Trapezes mithilfe von Dreiecken und Rechtecken.
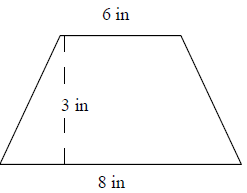
Lösung
Step 1:
Fläche des rechten Dreiecks = $ \ frac {1} {2} $ × b × h; b = Basis; h = Höhe.
Fläche von 2 rechtwinkligen Dreiecken = 2 × $ \ frac {1} {2} $ × b × h = 1 × 3 = 3 Quadratzoll.
Step 2:
Fläche des Rechtecks = l × w = 6 × 3 = 18 Quadratzoll
Step 3:
Fläche des Trapezes = Fläche der Dreiecke + Fläche des Rechtecks
= 3 + 18
= 21 Quadratmeter