Suchen des Bereichs eines rechtwinkligen Dreiecks oder des entsprechenden Rechtecks

Einführung

Area of a right triangle

Betrachten Sie ein Rechteck mit einer Länge von 1 Einheiten und einer Breite von w Einheiten. Zeichnen wir eine Diagonale und schneiden das Rechteck aus. Schneiden wir auch entlang der Diagonale, um zwei rechtwinklige Dreiecke zu bilden.

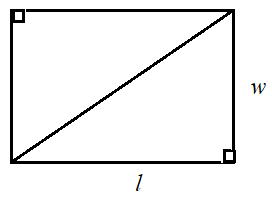
Es zeigt sich, dass die beiden rechtwinkligen Dreiecke die gleiche Größe und Fläche haben und kongruent sind. Die Fläche jedes rechtwinkligen Dreiecks ist also die Hälfte der Fläche des Rechtecks.

Fläche des rechtwinkligen Dreiecks = $ \ frac {1} {2} $ Fläche des Rechtecks = $ \ frac {1} {2} $ l × w

Die Länge l des Rechtecks ist die Basis b des rechtwinkligen Dreiecks und die Breite w des Rechtecks ist die Höhe h des rechtwinkligen Dreiecks.

So area of right triangle = $\mathbf{\frac{1}{2}}$ l × w = $\mathbf{\frac{1}{2}}$ b × h

Die Fläche eines rechtwinkligen Dreiecks ist die Hälfte der Fläche des entsprechenden Rechtecks

Beispiel 1:

Suchen Sie den Bereich des folgenden rechtwinkligen Dreiecks und das entsprechende Rechteck.

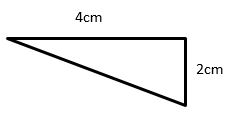
Lösung

Step 1:

Fläche des rechten Dreiecks = $ \ frac {1} {2} $ × b × h; b = Basis = 4; h = Höhe = 2

Step 2:

Fläche des rechten Dreiecks = $ \ frac {1} {2} $ × 4 × 2 = 4 Quadratzentimeter

Fläche des entsprechenden Rechtecks = b × h = 4 × 2 = 8 Quadratzentimeter

Beispiel 2:

Suchen Sie den Bereich des folgenden rechtwinkligen Dreiecks und das entsprechende Rechteck.

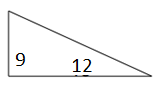
Lösung

Step 1:

Fläche des rechten Dreiecks = $ \ frac {1} {2} $ × b × h; b = Basis = 12; h = Höhe = 9

Step 2:

Fläche des rechten Dreiecks = $ \ frac {1} {2} $ × 12 × 9 = 54 quadratische Einheiten

Fläche des entsprechenden Rechtecks = b × h = 12 × 9 = 108 quadratische Einheiten